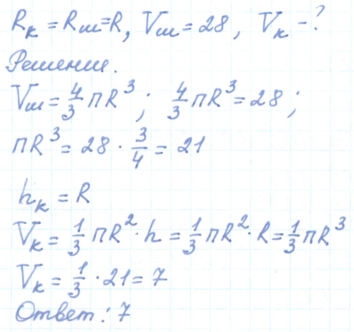В данной статье рассмотрим четыре задачи по стереометрии. Дана комбинация тел – конус и шар. Во всех заданиях речь идёт о конусе, который вписан в шар. Отмечу, что в условии взаимное расположение данных тел озвучено может быть по разному, например: «Конус вписан в шар» или «Около конуса описана сфера».
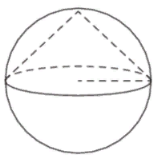
Суть одна – если сказать простым (нематематическим) языком, то конус находится «внутри» сферы, она содержит окружность его основания и вершину. Посмотрите на эскиз:
При решении необходимо знать формулы объёмов шара и конуса.
Объём шара:
Объём конуса:
*Эти формулы необходимо знать!
Площадь основания конуса является кругом, она равна:
Рассмотрим частный случай! Если высота конуса будет равна радиусу его основания, то формула объёма конуса будет иметь вид:
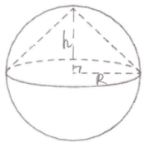
Эскиз:
Понятно, что центральным сечением такого конуса будет являться прямоугольный равнобедренный треугольник, причём высота проведённая из прямого угла разбивает его также на два прямоугольных равнобедренных треугольника:
Вспомним понятие образующей, оно часто используется в задачах с конусами, будет и в заданиях ниже.
Образующая конуса – это отрезок, соединяющий вершину конуса с точкой его основания. На предыдущем эскизе она обозначена буквой l.
Напрашивается простой вывод: образующих у конуса имеется бесконечное количество и все они равны.
На блоге, кстати, уже есть пара статей с шарами, можете посмотреть их «Задачи с шарами. Это просто!» и «Цилиндр описан около шара. Три задачи».
Теперь рассмотрим задачи:
245351. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.
Так как сказано, что радиус основания конуса равен радиусу шара, то становится понятно, что основание конуса совпадает с плоскостью центрального сечения шара.
Построим эскиз данной комбинации для наглядности (это осевое сечение):
Сказано, что высота конуса равна радиусу его основания (и, разумеется, радиусу шара). Запишем формулы объёмов шара и конуса:
Так как объём шара известен (он равен 28), можем вычислить радиус. Вернее, нам понадобится не сам радиус, а его куб:
Таким образом, объём конуса будет равен:
*Можно было обойтись без вычислений. Посмотрите, если сопоставить две формулы:
то видно, что объём шара в 4 раза больше объёма конуса.
Значит объём конуса будет равен 28/4 = 7.
То есть, задача решается практически устно.
Ответ: 7
245352. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара.
Задача обратная предыдущей, рисунок тот же.
Формулы:
Из формул понятно, что объём шара в 4 раза больше объёма конуса:
Таким образом, искомый объём равен 24.
Ответ: 24
316555. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна 
Здесь условие звучит по-другому, но тела расположены относительно друг друга абсолютно также, как и в предыдущих задачах – конус вписан в сферу, основание конуса совпадает с центральным сечением сферы.
Эскиз тот же, отметим радиус, высоту равную радиусу и образующую:
Задача сводится к использованию одной формулы. Рассмотрим прямоугольный треугольник (выделен жёлтым). По теореме Пифагора:
Радиус сферы равен семи.
Ответ: 7
316556. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен 
Эта задача обратная предыдущей, эскиз:
Рассмотрим прямоугольный треугольник (выделен жёлтым), х – это образующая. По теореме Пифагора:
Образующая конуса равна 56.
Ответ: 56
На этом всё. Успеха Вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 188. Найдите объём конуса.
Решение
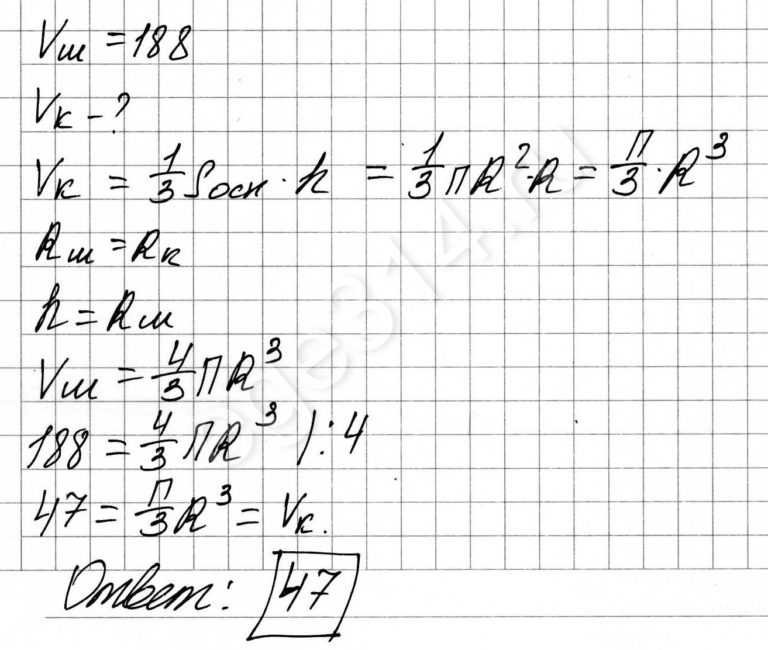
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 3.3 / 5. Количество оценок: 6
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
- Запись опубликована:06.04.2020
- Рубрика записи2. Стереометрия
- Автор записи:Andrei Maniakin
Конус вписан в шар
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.
Решение:
Антропий
10 октября, 16:56
-
Демид
10 октября, 17:08
0
Конус вписан в шар и радиус основания равен радиусу шара, значит и высота равна радиусу шара.
Имеем V шара = 4/3 ПR3=36
Объём конуса в 4 раза меньше:
Vконуса=1/3 ПR^2*H=1/3 ПR^3=1/4V шара=36/4=9
- Комментировать
- Жалоба
- Ссылка
Найди верный ответ на вопрос ✅ «Конус написан в шар. Радиус основания конуса равен радиусу шара. объём шара равен 36. найдите объём конуса …» по предмету 📙 Математика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Новые вопросы по математике
Главная » Математика » Конус написан в шар. Радиус основания конуса равен радиусу шара. объём шара равен 36. найдите объём конуса
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,651 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,893 -
разное
16,900
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.