Перейти к содержанию
Калькуляторы объёма и площади круга, цилиндра, куба, шара (сферы), конуса
На чтение 1 мин Просмотров 29.9к.
Обновлено 10.01.2022
Содержание
- Калькулятор площади и периметра (длины окружности) круга
- Калькулятор расчета площади и объёма шара (сферы)
- Калькулятор расчета объёма цилиндра
- Калькулятор расчета объёма параллелепипеда
- Калькулятор куба-объём, площадь поверхности
 В данном разделе вы найдете сборник калькуляторов на простые фигуры и рассчитать такие параметры как площадь, объем, периметр и прочие значения
В данном разделе вы найдете сборник калькуляторов на простые фигуры и рассчитать такие параметры как площадь, объем, периметр и прочие значения
Калькулятор площади и периметра (длины окружности) круга

Калькулятор расчета площади и объёма шара (сферы)

Калькулятор расчета объёма цилиндра

Калькулятор расчета объёма параллелепипеда

Калькулятор куба-объём, площадь поверхности

Расчет объема круга
Круг – это геометрическое место точек на плоскости, расстояние от которых до его центра, не превышает заданного числа, называемого радиусом этого круга.
Формула расчета объема круга:
V – объем круга;
S – площадь круга;
h – толщина круга.
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета объема круга. С помощью этого онлайн калькулятора расчета объема круга вы сможете вычислить объем круга по площади и толщине.
Все формулы объемов геометрических тел
1. Расчет объема куба
a – сторона куба
Формула объема куба, (V):
2. Найти по формуле, объем прямоугольного параллелепипеда
a , b , c – стороны параллелепипеда
Еще иногда сторону параллелепипеда, называют ребром.
Формула объема параллелепипеда, (V):
3. Формула для вычисления объема шара, сферы
R – радиус шара
По формуле, если дан радиус, можно найти объема шара, (V):
4. Как вычислить объем цилиндра ?
h – высота цилиндра
r – радиус основания
По формуле найти объема цилиндра, есди известны – его радиус основания и высота, (V):
5. Как найти объем конуса ?
R – радиус основания
H – высота конуса
Формула объема конуса, если известны радиус и высота (V):
7. Формула объема усеченного конуса
r – радиус верхнего основания
R – радиус нижнего основания
h – высота конуса
Формула объема усеченного конуса, если известны – радиус нижнего основания, радиус верхнего основания и высота конуса (V ):
8. Объем правильного тетраэдра
Правильный тетраэдр – пирамида у которой все грани, равносторонние треугольники.
а – ребро тетраэдра
Формула, для расчета объема правильного тетраэдра (V):
9. Объем правильной четырехугольной пирамиды
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
a – сторона основания
h – высота пирамиды
Формула для вычисления объема правильной четырехугольной пирамиды, (V):
10. Объем правильной треугольной пирамиды
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
a – сторона основания
h – высота пирамиды
Формула объема правильной треугольной пирамиды, если даны – высота и сторона основания (V):
11. Найти объем правильной пирамиды
Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
h – высота пирамиды
a – сторона основания пирамиды
n – количество сторон многоугольника в основании
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):
Как рассчитать периметр круга или длину окружности
На данной странице калькулятор поможет рассчитать периметр круга или длину окружности онлайн. Для расчета задайте радиус или диаметр.
Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).
Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.
[spoiler title=”источники:”]
http://www-formula.ru/2011-09-24-00-37-25
http://www.mozgan.ru/Geometry/PerimeterCircle
[/spoiler]
Лучший ответ
Данила fox
Гуру
(4815)
12 лет назад
s=pi*r*r
**LENOK**Ученик (142)
5 лет назад
Не правильно.
Остальные ответы
ALEKSANDR EFIMOV
Профи
(917)
12 лет назад
равен 0, круг двумерная фигура)
Валерия Смирнова
Мастер
(1102)
12 лет назад
какой обьем круга? круг – это тоже самое что и окружность, те замкнутая линия, не имеющая высоты.
обьем круга равен нулю. он двумерен
может вам нужен обьем шара?
Объем шара:
V=(4pr3)/3
где
p (пи) ~ 3,14
r – радиус шара
Анечка<Только твоя>
Ученик
(111)
12 лет назад
Объём – это площадь этого круга. Площадь круга радиуса равна Пи (3,14) * радиус2 (квадрат)
Hans
Мастер
(1674)
12 лет назад
Круг это плоскость!! ! какой обем может быть?
Алексей Соколов
Гуру
(4986)
12 лет назад
чему вас в школе учат? (((

a – сторона куба
Формула объема куба, (V):


a, b, c – стороны параллелепипеда
Еще иногда сторону параллелепипеда, называют ребром.
Формула объема параллелепипеда, (V):
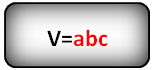

R – радиус шара
π ≈ 3.14
По формуле, если дан радиус, можно найти объема шара, (V):

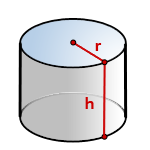
h – высота цилиндра
r – радиус основания
π ≈ 3.14
По формуле найти объема цилиндра, есди известны – его радиус основания и высота, (V):

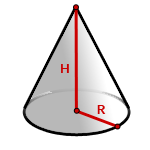
R – радиус основания
H – высота конуса
π ≈ 3.14
Формула объема конуса, если известны радиус и высота (V):
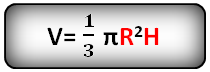
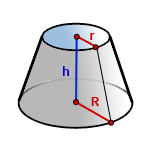
r – радиус верхнего основания
R – радиус нижнего основания
h – высота конуса
π ≈ 3.14
Формула объема усеченного конуса, если известны – радиус нижнего основания, радиус верхнего основания и высота конуса (V ):

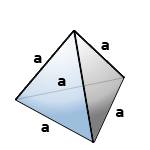
Правильный тетраэдр – пирамида у которой все грани, равносторонние треугольники.
а – ребро тетраэдра
Формула, для расчета объема правильного тетраэдра (V):
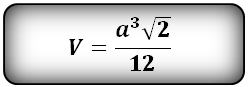
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
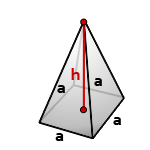
a – сторона основания
h – высота пирамиды
Формула для вычисления объема правильной четырехугольной пирамиды, (V):
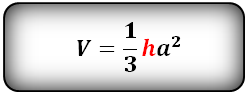
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
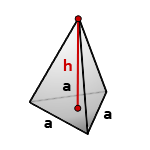
a – сторона основания
h – высота пирамиды
Формула объема правильной треугольной пирамиды, если даны – высота и сторона основания (V):

Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
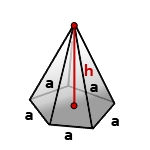
h – высота пирамиды
a – сторона основания пирамиды
n – количество сторон многоугольника в основании
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):
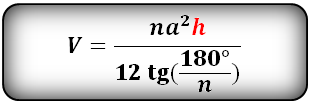
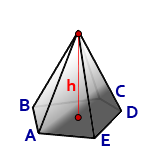
h – высота пирамиды
S – площадь основания ABCDE
Формула для вычисления объема пирамиды, если даны – высота и площадь основания (V):
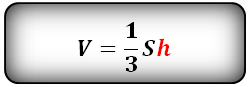
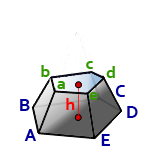
h – высота пирамиды
Sниж – площадь нижнего основания, ABCDE
Sверх – площадь верхнего основания, abcde
Формула объема усеченной пирамиды, (V):

Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.

R – радиус шара
h – высота сегмента
π ≈ 3.14
Формула для расчета объема шарового сегмента, (V):
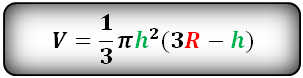
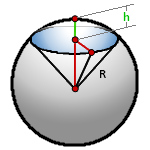
R – радиус шара
h – высота сегмента
π ≈ 3.14
Формула объема шарового сектора, (V):

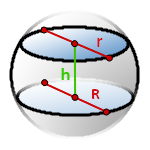
h – высота шарового слоя
R – радиус нижнего основания
r – радиус верхнего основания
π ≈ 3.14
Формула объема шарового слоя, (V):
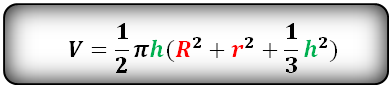
Содержание
- – Как рассчитать объем м3 круга?
- – Как посчитать объем воды в бочке?
- – Как вычислить м3 трубы?
- – Как определить объем цистерны?
- – Что надо сделать чтобы найти объём?
- – Как правильно считать в кубах?
- – Как по размерам вычислить объем литров?
- – Как определить объем резервуара?
- – Сколько кубов воды в 200 литровой бочке?
- – Сколько литров влазит в 200 литровую бочку?
Как рассчитать объем м3 круга?
объема в м3 и литрах
Объем цилиндра равен площади основания (круга) умноженной на высоту цилиндра.
Как посчитать объем воды в бочке?
Объем воды в бочке в литрах равен площади основания бочки в квадратных сантиметрах умноженной на высоту воды в бочке в см и разделить на тысячу.
Как вычислить м3 трубы?
Алгоритм программы основан на формуле определения объема цилиндра: V = π × d2 / 4 × L / 1000000, где d – внутренний диаметр трубы (мм), L – длина трубы (м), 1000000 – поправка на перевод единиц измерения.
Как определить объем цистерны?
Запрос звучал так — [Калькулятор] Должен вычислять объем цистерны, зная ее длинну, диаметр, толщину стенки. В такой постановке считаем объемы цилиндров, умножая длину на площадь окружности, соответственно учитывая стенки.
Что надо сделать чтобы найти объём?
По какой формуле можно найти объем?
- Зная массу и плотность V = m/ρ, где m – масса, а ρ – плотность
- Для геометрических фигур, например куб V = a^3 перемножить три стороны, а для цилиндра V = S*H площадь основания помножить на высоту
Как правильно считать в кубах?
Объем вычисляем по известной формуле: v = l х w х h, где v – объем коробки. Наглядно это выглядит так: допустим, длина коробки составила 70 см, ширина – 40 см, высота 50 см. Полученный объем будет составлять 140000 кубических сантиметров. Переводим величину в кубические метры, получаем 0,14 м3.
Как по размерам вычислить объем литров?
объем вычисляется по формуле: А*В*h, где А – длинна, В – ширина, h – высота; полученное значение переводится в литры, для чего умножается на 0,001.
Как определить объем резервуара?
Для того, чтобы определить объем какой-либо емкости, например, резервуара с чистой водой, нужно воспользоваться несложной формулой V = pr²h, где V — это объем, p — число «Пи» (3,1416), r — радиус измеряемой емкости, h — высота измеряемой емкости.
Сколько кубов воды в 200 литровой бочке?
Если Ваша бочка имеет объем 200 литров, то для полного помещения ее в землю необходимо выкопать 0,2 кубических метра земли или 1/5 часть 1 кубического метра.)
Сколько литров влазит в 200 литровую бочку?
Полный объем 216,5 л.
Интересные материалы:
Как вырастить фикус из черенка?
Как вырастить фундук из плода?
Как вырастить георгины на даче?
Как вырастить герань из семян?
Как вырастить гиацинт в горшке к 8 марта?
Как вырастить гладиолусы из луковицы?
Как вырастить гортензию Крупнолистную в горшке?
Как вырастить гортензию Метельчатую из черенка?
Как вырастить гранат?
Как вырастить Гузманию?
