Как найти объем кружки цилиндрической формы

Bowl is a round open top container, used to serve food, drink water, etc. Early bowls are found in China, ancient Greece, etc,. A bowl is also used as a unit of measurement defined by American units of measurement. Calculate volume of a bowl using the bowl volume
calculator. Enter the radius and height of the bowl in the volume of bowl calculator, it finds the spherical bowl volume. The bowl measurement can be found for different units in the volume of round bowl calculator.

Bowl is a round open top container, used to serve food, drink water, etc. Early bowls are found in China, ancient Greece, etc,. A bowl is also used as a unit of measurement defined by American units of measurement. Calculate volume of a bowl using the bowl volume
calculator. Enter the radius and height of the bowl in the volume of bowl calculator, it finds the spherical bowl volume. The bowl measurement can be found for different units in the volume of round bowl calculator.

Цилиндр является одной из распространенных форм пространственных тел, с которыми мы сталкиваемся ежедневно. Действительно, кружка, таблетка, дымоход, труба и другие предметы имеют цилиндрическую форму. В данной статье рассмотрим вопрос, как рассчитать объем цилиндра, используя различные известные параметры этой фигуры.

Определение цилиндра в геометрии

Прежде чем переходить к ответу на вопрос, как рассчитать объем цилиндра, разберемся, с какой фигурой мы имеем дело.

С геометрической точки зрения цилиндр образован двумя одномерными элементами. Первый – это кривая, которая является направляющей. Второй – это прямой отрезок, который называется образующей. Когда отрезок не находится в плоскости кривой, если его один конец соединить с кривой и перемещать параллельно самому себе вдоль нее, то мы получим цилиндрическую поверхность.

Под предоставленное определение подходит множество пространственных фигур, включая гиперболические, параболические и эллиптические цилиндры. Тем не менее в данной статье будем рассматривать только круглый прямой цилиндр. Круглым он называется по причине того, что его основания являются кругами (направляющая – окружность), а прямой он потому, что отрезок образующей перпендикулярен основаниям. Для наглядности описанный цилиндр показан на рисунке.

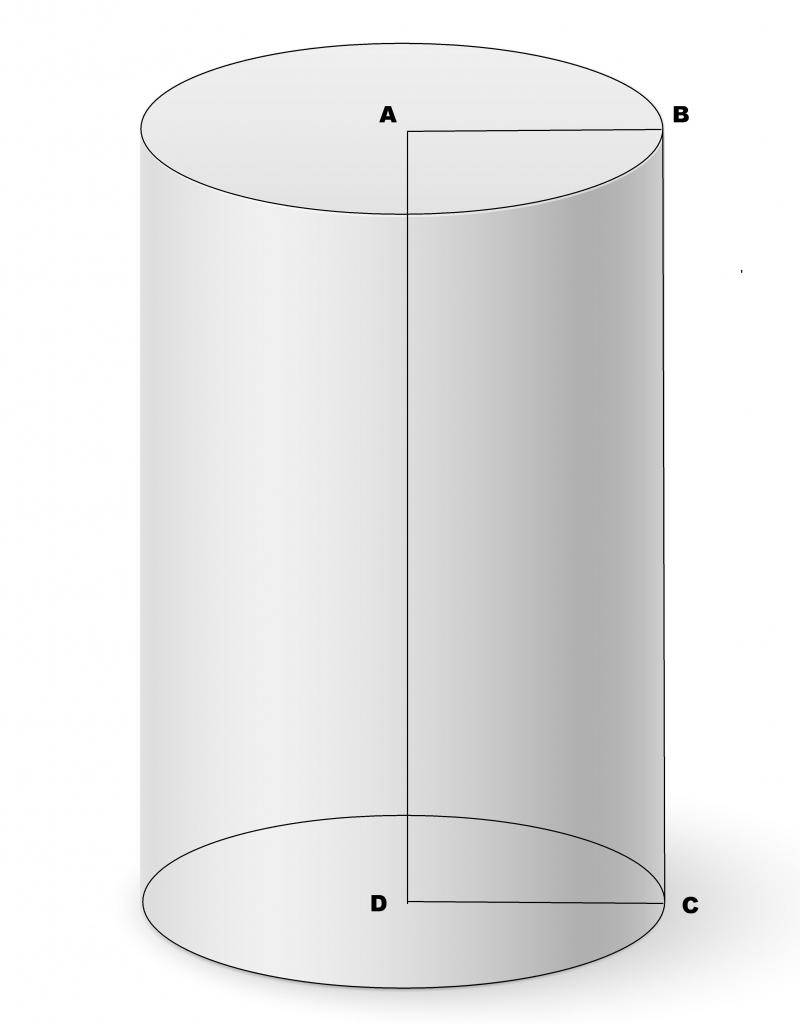
Как рассчитать объем цилиндра через радиус (диаметр) и высоту?

Ответом на этот вопрос является стандартная формула, которая справедлива для любого цилиндра и даже призмы. Запишем ее:

V = S_o * h

Поскольку в рассматриваемом случае основание – это правильный круг, то можно конкретизировать это выражение и переписать его в следующем виде:

V = pi * r² * h

Если известен диаметр, то найти объем цилиндра можно, используя такое выражение:

V = pi / 4 * d² * h

Определение объема цилиндра через площадь боковой поверхности

Еще одним способом рассчитать объем цилиндра, является использование площади его боковой поверхности. Этой поверхностью называется совокупность точек всех образующих, которые соединяют два основания фигуры. Боковая поверхность имеет цилиндрическую форму. Если ее разрезать вдоль одной из образующих и раскрыть, то получится развертка фигуры, показанная ниже.

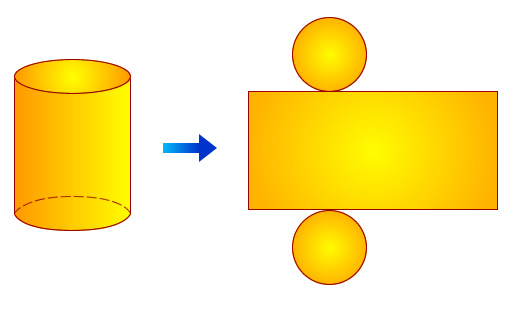
Видно, что в развернутом виде боковая поверхность является обычным прямоугольником, стороны которого равны высоте и длине окружности основания. Последний факт позволяет записать формулу для площади S_b этой фигуры:

S_b = 2 * pi * r * h

Если известен радиус r фигуры, тогда высота ее будет равна:

h = S_b / (2 * pi * r)

Тогда для объема V формула для цилиндра запишется в виде:

V = r * S_b / 2

Если же известна площадь S_b и высота h, тогда радиус фигуры будет равен:

r = S_b / (2 * pi * h)

Подставляя его в выражение для объема, приходим к следующей формуле:

V = S_b² / (4 * pi * h)

Можно заметить, что обе формулы с использованием боковой площади S_b соответствуют размерности объема (м³).

Важно понимать, что объем круглого прямого цилиндра можно определить только в том случае, если известны какие-нибудь два его параметра.

Задача на расчет объема цилиндра через площадь его полной поверхности

Предположим, что цилиндр имеет высоту 21 см, а площадь его развертки составляет 335 см². Необходимо определить объем фигуры.

Ни одна из приведенных выше формул не способна дать нам искомый ответ. В таком случае, как рассчитать объем цилиндра? Как выше было сказано, достаточно знать любые два параметра фигуры, чтобы определить величину V. В данном случае запишем сначала формулу для общей площади цилиндра:

S = S_b + 2 * S_o = 2 * pi * r * h + 2 * pi * r²

Подставим в это равенство известные данные, получим:

r² + 21 * r – 53,34 = 0

После подстановки данных мы разделили левую и правую части на 2 * pi и перенесли все члены в одну часть равенства.

Таким образом, перед нами стоит задача решения квадратного уравнения. Используем стандартный метод решения через дискриминант, имеем:

дискриминант D = 654,36;

r = 2,29 см.

При решении уравнения мы отбросили отрицательный корень.

Теперь для определения объема цилиндра можно воспользоваться формулой с параметрами r и h. Подставляя их в указанную формулу, приходим к ответу на задачу: V = 345,8 см³.

Всего: 45    1–20 | 21–40 | 41–45

Добавить в вариант

Всего: 45    1–20 | 21–40 | 41–45

Перейти к контенту

Задание

Даны две кружки цилиндрической формы. Первая кружка в четыре раза ниже второй, а вторая в полтора раза шире первой. Во сколько раз объём первой кружки больше объёма второй?

Решение

1. Для решения данной задачи необходимо знать формулу для нахождения объема цилиндра (так как две кружки имеют форму цилиндра):

Объем цилиндра равен произведению его высоты на площадь основания (основание цилиндра – это круг, поэтому площадь основания равна площади круга):

V = h*S_осн = h*π*r² = h*π*D²/4

1. Найдем объем первой кружки (которая ниже):

V₁ = h*π*D²/4

1. Найдем объем второй кружки:

V₂ = 4h*π*(1,5*D)²/4

1. Осталось найти, во сколько объем первой кружки меньше второй:

V₂ / V₁ = 4h*π*(1,5*D)²/4:(h*π*D²/4) = в 9 раз объем первой кружки меньше объема большой.

Ответ: 9