ucoviniedema463
Вопрос по геометрии:
Найдите объем куба,если площадь его диагонального сечения равна S
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
knalincate
Обозначим сторону куба за а.
Диагональ основания равна а√2, а площадь диагонального сечения равна а²√2.По условию а²√2 = S. Отсюда а = √(S/√2).Объём куба V = a³ = (√(S/√2))³ = (S/√2)*√(S/√2)
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
помогите пожалуйста. вычислить объем куба,если площадь его диогонального сечения рвна М.
Ученик
(148),
на голосовании
11 лет назад
Голосование за лучший ответ
Alex Alexahin
Гуру
(3793)
11 лет назад

Площадь диагонального сечения заштрихована М=диагональ стороны*высоту куба
У куба все стороны=а
Диагональ стороны с^2=a^2+a^2 по теореме Пифагора
c^2=2*a^2
c=(2*a^2)^(1/2)=а*(2)^(1/2)
М=с*а=а*(2*a^2)^(1/2)=а^2*sqrt(2)
отсюда сторона а=(М/sqrt(2))^(1/2)
Объём куба=а^3=(М/sqrt(2))^(3/2)
=M*sqrt(M)/(8)^(1/4)
Загрузить PDF
Загрузить PDF
Объем трехмерной фигуры является величиной, которая характеризует пространство, занимаемое этой фигурой. Объем равен произведению длины фигуры на ее ширину и на высоту. Куб — это трехмерная фигура, у которой длина, ширина и высота одинаковые, то есть все ребра куба равны.[1]
Поэтому вычислить объем куба довольно просто, если знать значение его ребра. А ребро можно найти по площади поверхности куба.
-

1
Запишите формулу для вычисления площади поверхности куба. Формула выглядит так:
, где
— ребро куба.[2]
- Чтобы вычислить объем куба, нужно перемножить значения трех его ребер (длину, ширину и высоту).[3]
У куба длина, ширина и высота равны, поэтому нужно найти значение одного (любого) ребра, чтобы вычислить объем куба. Имейте в виду, что для вычисления площади поверхности куба нужно знать значение ребра; поэтому, если площадь поверхности куба дана, вы с легкостью найдете его ребро, а затем вычислите объем куба.
- Чтобы вычислить объем куба, нужно перемножить значения трех его ребер (длину, ширину и высоту).[3]
-

2
В формулу подставьте значение площади поверхности куба. Площадь поверхности должна быть дана в задаче.
-

3
Разделите значение площади поверхности куба на 6. Так вы найдете значение
.
-

4
Извлеките квадратный корень. Так вы найдете значение
, то есть значение ребра куба.
Реклама
-

1
Запишите формулу для вычисления объема куба. Формула выглядит так:
, где
– объем куба,
— ребро куба.[4]
-

2
В формулу подставьте значение ребра куба. Это значение вы нашли по известной площади поверхности куба.
- Например, если ребро куба равно 4 см, формула запишется так:
.
- Например, если ребро куба равно 4 см, формула запишется так:
-

3
Возведите в куб (в третью степень) значение ребра куба. Сделайте это на калькуляторе или просто умножьте «x» на себя три раза. Так вы найдете объем куба в кубических единицах измерения.
Реклама
Что вам понадобится
- Карандаш/ручка
- Бумага
Об этой статье
Эту страницу просматривали 32 956 раз.
Была ли эта статья полезной?
Найдите объем куба, если площадь его диагонального сечения равна 2.
На этой странице сайта вы найдете ответы на вопрос Найдите объем куба, если площадь его диагонального сечения равна 2?,
относящийся к категории Геометрия. Сложность вопроса соответствует базовым
знаниям учеников 10 – 11 классов. Для получения дополнительной информации
найдите другие вопросы, относящимися к данной тематике, с помощью поисковой
системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и
задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям.
Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы
помогут найти нужную информацию.
Объём куба
- Главная
- /
- Математика
- /
- Геометрия
- /
- Объём куба
Чтобы найти объём куба воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Объём куба через ребро
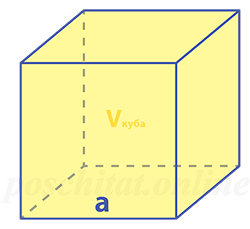
Чему равен объём куба, если:
ребро a =
Vкуба =
0
Округление ответа:
Объём куба через диагональ
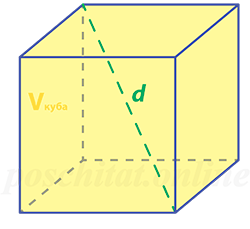
Чему равен объём куба, если:
диагональ d =
Vкуба =
0
Округление ответа:
Объём куба через площадь поверхности
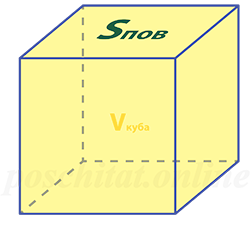
Чему равен объём куба, если:
Sпов =
Vкуба =
0
Округление ответа:
Теория
Как найти объём куба зная длину ребра
Чему равен объём куба Vкуба, если длина его рёбер a:
Формула
Vкуба = a³
Пример
Для примера, найдём объём куба, у которого рёбра a = 5 см:
Vкуба = 5³ = 125 см³
Как найти объём куба зная диагональ
Чему равен объём куба Vкуба, если его диагональ d:
Формула
Vкуба = d³ ⁄3√3
Пример
Для примера, найдём объём куба, длина диагонали которого d = 9 см:
Vкуба = 9³ / 3√3 ≈ 729 / 5,2 ≈ 140 см³
Как найти объём куба зная площадь поверхности
Чему равен объём куба Vкуба, если площадь поверхности этого куба Sпов:
Формула
Vкуба = √Sпов³ ⁄6√6
Пример
Для примера, найдём объём куба, площадь поверхности которого Sпов = 24 см²:
Vкуба = √24³ / 6√6 = 24√24 / 6√6 = 4√4 = 8 см³
