В данной публикации мы рассмотрим, как можно найти объем куба и разберем примеры решения задач для закрепления материала.
- Формула вычисления объема куба
- Примеры задач
Формула вычисления объема куба
1. Через длину ребра
Объем (V) куба равняется произведению его длины на ширину на высоту. Т.к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.
V = a ⋅ a ⋅ a = a3

2. Через длину диагонали грани
Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: a=d/√2.

Следовательно, вычислить объем куба можно так:
![]()
Примеры задач
Задание 1
Вычислите объем куба, если его ребро равняется 5 см.
Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см3.
Задание 2
Известно, что объем куба равен 512 см3. Найдите длину его ребра.
Решение:
Пусть ребро куба – это a. Выведем его длину из формулы расчета объема:![]()
Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.
Решение:
Применим формулу, в которой используется диагональ грани:
![]()
Слайд 1
Урок математики.3 класс Объём прямоугольного параллелепипеда.
Слайд 2
Немного из истории… Нас окружает множество предметов. Они отличаются формой, размерами, материалом, из которого изготовлены, окраской, …. Людей интересуют разные качества этих предметов. Математиков интересуют их форма и размеры.
Слайд 4
Немного из истории… Стакан и карандаш имеют форму цилиндра. Заметьте, что формы предметов очень разнообразны и не для всякой формы имеется специальное название.
Слайд 5
Какой многогранник мы сегодня рассмотрим?
Слайд 6
Тема: Прямоугольный параллелепипед Правильно напишите! Давайте внимательно исследуем параллелепипед!
Слайд 7
Прямоугольный параллелепипед
Слайд 8
Прямоугольный параллелепипед
Слайд 9
Ваша работа будет успешной, если вы: ● покажете знания изученных величин и единиц их измерения. ● будете активно участвовать в исследовании, выражать собственное мнение и давать высказываться другим. ●ваша деятельность на уроке покажет, что вы понимаете, что такое объем и можете его вычислить. ● сможете вывести формулу объема куба и прямоугольного параллелепипеда.
Слайд 10
Какие предметы имеют форму прямоугольного параллелепипеда? т о р т
Слайд 11
А В С D 1 С 1 Вершины – точки Грани – прямоугольники Ребра – отрезки А 1 D В 1
Слайд 12
Что такое объем?
Слайд 13
Кубический сантиметр
Слайд 14
Объем прямоугольного параллелепипеда
Слайд 16
Об ъ ем прямоугольного пара лл ел е пипеда
Слайд 17
1м 3 Единицы объема. 1дм 3 1см 3 1мм 3 1000 1000 1000
Слайд 18
a V= а х а х а Объем куба a a
Слайд 19
3м 20м 6 м Чтобы сделать бассейн в земле выкопали котлован в форме прямоугольного параллелепипеда длиной 20 м, шириной 6 м и глубиной 3 м. Сколько кубических метров земли пришлось вынуть?
Слайд 20
3м 6 м 5 м Воздуха ? м 3
Слайд 21
Длина аквариума 8 дм, ширина 4 дм, а высота 5 дм. Сколько литров воды надо влить в этот аквариум, чтобы уровень воды был ниже верхнего края аквариума на 1 дм? 5 дм 8 дм 4 дм 1 дм
Слайд 22
3м 7 м 4 м 1 рулон 10 м 2 S окон и дверей 9 м 2
Слайд 23
1м 3 сена весит 6 ц ширина 6 м Длина 10 м высота 4 м V- ?
Слайд 24
Объем бассейна равен 100 м 3 , а стороны основания 10 м и 5 м. Сколько квадратных метров кафельной плитки ушло на облицовку бассейна? 10 м 5 м V = 100 м 3 110 м 2 160 м 2 3 1 2 4 ПОДУМАЙ! ВЕРНО! ПОДУМАЙ! ПОДУМАЙ! 60 м 2 9 0 м 2
Куб – это трехмерная фигура, представляющая собой правильный многогранник, все грани которого квадраты. Чтобы найти объем куба достаточно знать только длину его стороны (они у куба равны).
Чтобы найти объем куба можно воспользоваться калькулятором, либо одной из подходящих формул, которые мы приводим ниже.
Содержание:
- калькулятор объема куба
- формула объема куба через ребро
- формула объема куба через диагональ грани
- формула объема куба через периметр грани
- формула объема куба через диагональ куба
- формула объема куба через площадь полной поверхности
- примеры задач
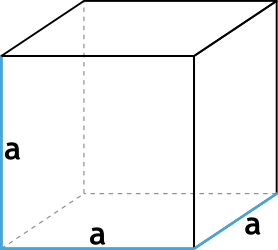
Формула объёма куба через ребро
Формула объёма куба через диагональ грани
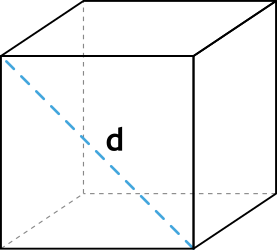
{V = Big( dfrac{d}{sqrt{2}} Big) ^3}
d – диагональ грани куба
Формула объёма куба через периметр грани
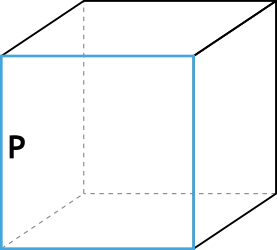
{V= Big( dfrac{P}{4} Big) ^3}
P – периметр грани куба
Формула объёма куба через диагональ куба
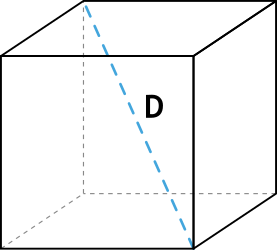
{V= dfrac{D^3}{3sqrt{3}}}
D – диагональ куба
Формула объёма куба через площадь полной поверхности
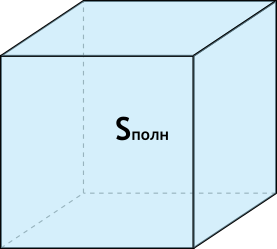
{V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}}}
Sполн – диагональ куба
Примеры задач на нахождение объема куба
Задача 1
Чему равен объём куба с ребром 5 см?
Решение
Для нахождения объема куба, когда известа длина ребра, воспользуемся первой формулой:
V=a ^ 3 = 5 ^ 3 = 125 : см^3
Ответ: 125 см³
Воспользуемся калькулятором для проверки полученного результата.
Задача 2
Найти объем куба, если площадь его поверхности равна 96 см².
Решение
В данном примере нам подойдет эта формула:
V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}} = dfrac{sqrt{{96}^3}}{6sqrt{6}} = dfrac{sqrt{96 cdot 96 cdot 96}}{6sqrt{6}} = dfrac{96 sqrt{96}}{6sqrt{6}} = dfrac{96 sqrt{16 cdot 6}}{6sqrt{6}} = dfrac{96 cdot 4 sqrt{6}}{6sqrt{6}} = dfrac{384 sqrt{6}}{6sqrt{6}} = 64 : см^3
Ответ: 64 см³
Проверить ответ поможет калькулятор .
Также на нашем сайте вы можете найти объем конуса.
Напиши формулу объема куба со стороной a. Найди объем куба, если:
1) a = 4 см;
2) a = 60 м;
3) a = 900 см.

reshalka.com
ГДЗ учебник по математике 3 класс Петерсон. 31 урок. Формула объема прямоугольного параллелепипеда. Номер №5
Решение а
V = a * a * a = 4 * 4 * 4 = 16 * 4 = 64
(
с
м
3
)
− объем куба.
Ответ: 64
с
м
3
Решение б
V = a * a * a = 60 * 60 * 60 = 3600 * 60 = 216000
(
м
3
)
− объем куба.
×
36
6
¯
216
Ответ: 216000
м
3
Решение в
V = a * a * a = 9 * 9 * 9 = 81 * 9 = 729
(
м
3
)
− объем куба.
×
81
9
¯
729
Ответ: 729
м
3
|
Как правильно рассчитать объем куба?
Чтобы рассчитать объём куба, надо длину его ребра (а у куба они все одинаковые) взять в куб. Например, длина ребра (Н) 2 см, объём будет рассчитываться так: V = Н х Н х Н, 2 х 2 х 2 = 8. То есть, объём куба с длиной ребра 2 см будет составлять 8 см кубических. автор вопроса выбрал этот ответ лучшим chela 10 лет назад Чтобы найти объем куба, нужно длину умножить на ширину и на высоту. Так как в кубе это все одинаково, достаточно иметь только один размер. Если эти размеры неизвестны, а известна любая диагональ любой грани, то можно найти объем куба за диагональю грани: V=(d*корень двух)все в кубе где d – длина диагонали грани
Проповедник 10 лет назад .чтобы правильно рассчитать объем квадратного куба, нужно сначала найти длину одной из его сторон. Поскольку стороны его все равны, а он квадратный, то объем куба будет рассчитываться по формуле V=a^3, где V- это объем, а- это длина стороны
Андрей0817 9 лет назад Объём вычисляется путём умножения длины, высоты и ширины. Длина – 5 см, ширина – 5 см, высота 5 см = 5*5*5=125 см.
.Здесь легко вычислить объём. А вот если вам привезли машину дров и говорят, что там 7 кубов, то это легко проверить самому. Также , надо умножить длину и ширину кузова машины и эту сумму умножить на высоту уложенных дров. Потом эту сумму ещё и умножить на коэффициент плотности. Он может быть – 0,8 – если дрова сложены плотно друг к другу, а если не плотно, то от 0,7 и до 0,5. Чем плотнее лежат дрова, тем больше коэффициент.
Nikolai Sosiura 9 лет назад Для того, чтобы найти объём куба, нам понадобится произвести умножение некоторых величин. Сначала надо узнать площадь основания куба. Нам придётся умножить высоту на ширину (hxW = A), где: А- площадь, h- высота, W- ширина. Далее множим высоту на уже известную нам площадь основания куба (LxA = V), где V- объём, L- длинна, A- площадь.
Lilka-g 9 лет назад Если мы умножим Длину куба на ширину куба, а затем эту цифру умножим на высоту куба, то получим объем куба. Например если у куба 3 мм ширина, 2 мм длина и 5 мм высота будет так. 3*2=6*5=30. В итоге в этом случаи объем куба будет 30 миллиметров.
Edvard 9 лет назад Это вопрос мне задавали, если не ошибаюсь, еще в шестом классе. Найти объем куба очень легко. Нужно только умножить длину, ширину и высоту куба. Другими словами- возвести одну грань куба в третью степень. Как я уже говорил, нчего сложного.
Roxrite 9 лет назад Если неизвестна длина стороны ребра куба, то необходимо её просто измерить. Допустим, она равна 3 см. Далее возводим в куб (третью степень) это число. Получается 3 в кубе – это 27 см3. Ответ: 27 кубических сантиметров.
Solnce lychik 9 лет назад Объем куба пишется буквой V. А формула достаточно проста: где a это длина грани куба d это диагональ его квадратной грани. у куба двенадцать граней и все они равны. Вот такими формулами можно вычеслить объем куба. Знаете ответ? |


