Объем куба при заданном радиусе описанного цилиндра
Идти
Объем куба = (sqrt(2)*Описанный цилиндр Радиус куба)^(3)
Объем куба с учетом радиуса средней сферы
Идти
Объем куба = (sqrt(2)*Радиус средней сферы куба)^(3)
Объем куба с учетом пространственной диагонали
Идти
Объем куба = (Космическая диагональ куба/sqrt(3))^3
Объем куба при заданном радиусе окружности
Идти
Объем куба = (2/sqrt(3)*Окружность Радиус куба)^(3)
Объем куба по диагонали грани
Идти
Объем куба = (Диагональ грани куба/sqrt(2))^(3)
Объем куба при заданном отношении поверхности к объему
Идти
Объем куба = (6/Отношение поверхности к объему куба)^(3)
Объем куба с учетом площади боковой поверхности
Идти
Объем куба = (Площадь боковой поверхности куба/4)^(3/2)
Объем куба с учетом общей площади поверхности
Идти
Объем куба = (Общая площадь поверхности куба/6)^(3/2)
Объем куба при заданном радиусе вписанного цилиндра
Идти
Объем куба = (2*Вписанный цилиндр Радиус куба)^(3)
Объем куба с учетом периметра грани
Идти
Объем куба = (Лицевой периметр куба/4)^(3)
Объем куба с учетом радиуса Insphere
Идти
Объем куба = (2*Insphere Радиус куба)^(3)
Объем куба с учетом площади грани
Идти
Объем куба = Площадь грани куба^(3/2)
Объем куба по периметру
Идти
Объем куба = (Периметр куба/12)^(3)
Объем куба
Идти
Объем куба = Длина ребра куба^3
Объем куба с учетом пространственной диагонали
Идти
Объем куба = (Космическая диагональ куба/sqrt(3))^3
Объем куба при заданном радиусе окружности
Идти
Объем куба = (2/sqrt(3)*Окружность Радиус куба)^(3)
Объем куба с учетом общей площади поверхности
Идти
Объем куба = (Общая площадь поверхности куба/6)^(3/2)
Объем куба
Идти
Объем куба = Длина ребра куба^3
Куб (или гексаэдр) — это правильный многогранник, который состоит из многоугольников, являющихся квадратами.
У куба 12 ребер – отрезков, которые являются сторонами квадратов (граней куба).
Также он имеет 8 вершин и 6 граней.
Онлайн-калькулятор объема куба
Формула объема куба
Для нахождения объема куба нужно перемножить его измерения – длину, ширину и высоту. Исходя из того, что куб состоит из квадратов, все его измерения одинаковы и численно равны длине ребра.
Формула для вычисления объема куба такова:
V=a3V=a^3
где aa — длина ребра куба.
Рассмотрим несколько примеров.
Найти объем куба, если периметр PP его грани aa равен 16 cм.16text{ cм.}
Решение
P=16P=16
Периметр PP грани куба связан с длиной его ребра aa по формуле:
P=a+a+a+a=4⋅aP=a+a+a+a=4cdot a
16=4⋅a16=4cdot a
a=164=4a=frac{16}{4}=4
Найдем объем нашего тела:
V=a3=43=64 см3V=a^3=4^3=64text{ см}^3
Ответ: 64 см3.64text{ см}^3.
Одна четвертая часть диагонали квадрата равна 3 см.3text{ см.} Найти объем куба, образованного данным четырехугольником.
Решение
Пусть dd — диагональ фигуры, тогда по условию:
d4=3frac{d}{4}=3
d=4⋅3=12d=4cdot 3=12
Найдем сторону этого квадрата. Обратимся за помощью к теореме Пифагора:
a2+a2=12a^2+a^2=12,
где aa — сторона квадрата.
2⋅a2=122cdot a^2=12
a=6a=sqrt{6}
Приходим к окончательным расчетам для объема:
V=a3=(6)3=66 см3V=a^3=(sqrt{6})^3=6sqrt{6}text{ см}^3
Ответ: 66 см3.6sqrt{6}text{ см}^3.
Чуть более сложный пример.
В куб вписан шар, площадь SS которого равна 64π64pi. Найти объем куба.
Решение
S=64πS=64pi
Первый шагом является нахождение радиуса RR данного шара. Формула его площади такова:
S=4⋅π⋅R2S=4cdotpicdot R^2
64π=4⋅π⋅R264pi=4cdotpicdot R^2
64=4⋅R264=4cdot R^2
644=R2frac{64}{4}=R^2
16=R216=R^2
R=4R=4
Для куба радиус вписанного шара является половиной его стороны aa:
a=2⋅R=2⋅4=8a=2cdot R=2cdot4=8
Объем вычисляется следующим образом:
V=a3=83=512 см3V=a^3=8^3=512text{ см}^3
Ответ: 512 см3.512text{ см}^3.
На Студворке вы можете оформить заказ контрольных работ для студентов по самым низким ценам!
Тест по теме «Объем куба»
Как определить объем куба
Куб – это объемная геометрическая фигура, составленная из шести граней («гексаэдр») правильной формы. Ограниченное гранями внутреннее пространство такого многогранника можно рассчитать, имея сведения о некоторых из его параметров. В простых случаях бывает достаточно знания всего одного из них – такова особенность объемных фигур с гранями одинаковой формы.

Инструкция
Если есть возможность узнать из условий задачи или измерить самостоятельно длину любого ребра (a) куба, в вашем распоряжении будут сразу и длина, и ширина, и высота многогранника. Для вычисления объема (V) гексаэдра перемножьте эти три параметра, то есть просто возведите в куб длину ребра: V = a³.
По площади грани (s) тоже возможно вычислить объем этой фигуры. Так как площадь квадрата равна второй степени длины его стороны, вы можете выразить через нее длину ребра куба: a = √s. Подставьте это выражение в формулу объема из предыдущего шага, чтобы получить такое равенство: V = (√s)³.
Известная длина диагонали (l) одной грани является достаточным параметром для нахождения объема куба потому, что по теореме Пифагора через нее можно выразить длину ребра этой объемной фигуры: a = l/√2. Возведите это выражение в третью степень, чтобы получить искомую величину: V = (l/√2)³.
Диагональ (L) не отдельной грани, а гексаэдра в целом – это отрезок, который соединяет две вершины, симметричные относительно центра фигуры. Длина такого отрезка больше длины одного ребра в число раз, равное корню из тройки, поэтому для вычисления объема фигуры поделите длину диагонали на корень из 3, а результат возведите в куб: V = (l/√2)³.
Полная площадь поверхности (S) гексаэдра складывается из шести площадей граней, каждая из которых вычисляется возведением в квадрат длины ребра. Воспользуйтесь этим при вычислении объема фигуры – найдите размер ребра, разделив общую площадь поверхности на шестерку и найдя корень из полученного значения, а затем возведите результат в куб: V = (√(S/6))³.
Если вам известен радиус (r) вписанной в куб сферы, возведите его в куб и умножьте на восьмерку – результат будет объемом этого многогранника: V=r³*8. Через диаметр (d) такой сферы выразить объем еще проще, так как его размер равен длине ребра гексаэдра: V = d³.
Формула для вычисления объема по радиусу (R) описанной около куба сферы немного сложнее – после возведения его в третью степень и умножения на восьмерку, разделите полученное значение на куб корня из тройки: V=R³*8/(√3)³.
Источники:
- как узнать объём куба
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

a – сторона куба
Формула объема куба, (V):


a, b, c – стороны параллелепипеда
Еще иногда сторону параллелепипеда, называют ребром.
Формула объема параллелепипеда, (V):
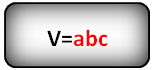

R – радиус шара
π ≈ 3.14
По формуле, если дан радиус, можно найти объема шара, (V):

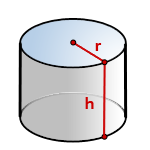
h – высота цилиндра
r – радиус основания
π ≈ 3.14
По формуле найти объема цилиндра, есди известны – его радиус основания и высота, (V):

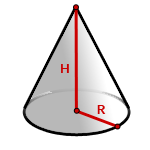
R – радиус основания
H – высота конуса
π ≈ 3.14
Формула объема конуса, если известны радиус и высота (V):
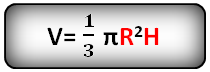
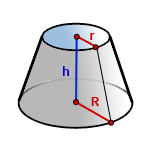
r – радиус верхнего основания
R – радиус нижнего основания
h – высота конуса
π ≈ 3.14
Формула объема усеченного конуса, если известны – радиус нижнего основания, радиус верхнего основания и высота конуса (V ):

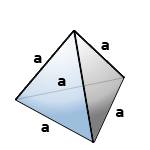
Правильный тетраэдр – пирамида у которой все грани, равносторонние треугольники.
а – ребро тетраэдра
Формула, для расчета объема правильного тетраэдра (V):
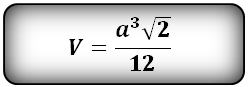
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
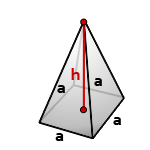
a – сторона основания
h – высота пирамиды
Формула для вычисления объема правильной четырехугольной пирамиды, (V):
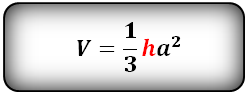
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
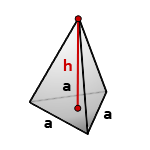
a – сторона основания
h – высота пирамиды
Формула объема правильной треугольной пирамиды, если даны – высота и сторона основания (V):

Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
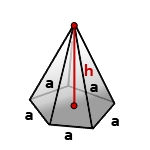
h – высота пирамиды
a – сторона основания пирамиды
n – количество сторон многоугольника в основании
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):
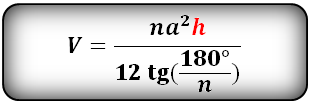
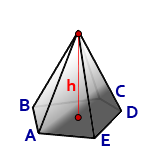
h – высота пирамиды
S – площадь основания ABCDE
Формула для вычисления объема пирамиды, если даны – высота и площадь основания (V):
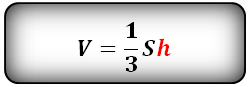
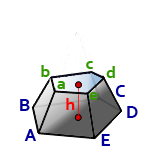
h – высота пирамиды
Sниж – площадь нижнего основания, ABCDE
Sверх – площадь верхнего основания, abcde
Формула объема усеченной пирамиды, (V):

Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.

R – радиус шара
h – высота сегмента
π ≈ 3.14
Формула для расчета объема шарового сегмента, (V):
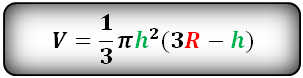
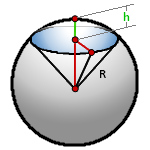
R – радиус шара
h – высота сегмента
π ≈ 3.14
Формула объема шарового сектора, (V):

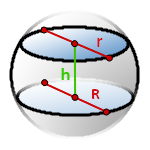
h – высота шарового слоя
R – радиус нижнего основания
r – радиус верхнего основания
π ≈ 3.14
Формула объема шарового слоя, (V):
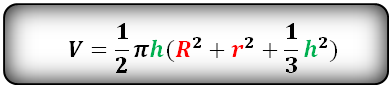
Найти объем куба
Пример решили: 27755 раз
Сегодня решили: 0 раз
Введите длину стороны куба
Сторона a
Введите e-mail, чтобы не потерять решение
Указывая электронную почту, я соглашаюсь с условиями обработки персональных данных
Вычисление объема куба
Куб – частный случай параллелограмма и призмы, многогранник, каждая грань которого является квадратом.
Каждая сторона куба: длина, ширина и высота – равны между собой.

Для вычисления объема куба необходимо длину его стороны возвести в третью степень.
Объем куба можно вычислить по формуле:
$$V = a^3$$
Примеры решений
- Найдите объем куба, если его сторона равна 2 см.
Посмотреть решениеДано:
$$ a = 2 см $$
Решение:
По формуле для объема куба:
$$ V = a^3 $$
$$ V = 2^3 = 8 см^3 $$
Ответ:
$$ V = 8 см^3 $$
- Найдите объем куба, если его площадь поверхности равна 24 см².
Посмотреть решениеДано:
$$ S = 24 см^2 $$
Решение:
Найдем сторону куба:
$$ S = 6 cdot a^2 $$
$$ a = sqrt{ frac{S}{6} } = sqrt{ frac{24}{6} } = 2 см $$
По формуле для объема куба:
$$ V = a ^3 $$
$$ 2^3 = 8 см^3 $$
Ответ:
$$ V = 8 см^3 $$
- Найдите объем куба, если радиус вписанной сферы равен 3 см.
Посмотреть решениеДано:
$$ r = 3 см $$
Решение:
Найдем сторону куба:
$$ r = frac{1}{2} cdot a $$
$$ a = r cdot 2 = 2 cdot 3 = 6 см $$
По формуле для объема куба:
$$ V = a ^3 $$
$$ V = 6^3 = 216 см^3 $$
Ответ:
$$ V = 216 см^3 $$
- Найдите объем куба, если радиус описанной сферы равен 2*√3 см.
Посмотреть решениеДано:
$$ R = 2 cdot sqrt{3} см $$
Решение:
Найдем сторону куба, зная радиус описанной сферы:
$$ R = frac{ sqrt{3} }{2} cdot a $$
$$ a = frac{ (R cdot 2) }{ sqrt{3} } = 4 см $$
По формуле для объема куба:
$$ V = a ^3 $$
$$ V = 4^3 = 64 см^3 $$
Ответ:
$$ V = 64 см^3 $$
- Найдите объем куба, если диаметр вписанной сферы равен 4 см.
Посмотреть решениеДано:
$$ d=4 см $$
Решение:
Найдем сторону куба, зная диаметр вписанной сферы:
$$ d=a $$
$$ a = 4 см $$
По формуле для объема куба:
$$ V = a ^3 $$
$$ V = 4^3 = 64 см^3 $$
Ответ:
$$ V = 64 см^3 $$
Попробуйте другие сервисы

