trealoingeom907
Вопрос по геометрии:
Шар, объем которого равен П, вписан в куб. Найдите объем куба. Помогите,пожалуйста!

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
fonsablyil299
Vкуба=а³ (а – сторона куба)
Vшара=4/3πr³
По условию объем шара равен π (пи)
Значит можем приравнять 4/3πr³=π, откуда находим, что
r³=3/4; r=∛3/4
Радиус вписанного в куб шара равен 1/2а, значит r=2a ⇒ Vкуба равен (2r)³
Vкуба= (2*∛3/4)³=8*3/4=6
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Шар, объём которого равен 12π, вписан в куб. Найдите объём куба.
Источник: Досрочная волна 2014
Решение:
Из формулы объёма шара найдём радиус:
V_{шар}=frac{4}{3}pi R^{3}=12pi\frac{4}{3}pi R^{3}=12pi\frac{4}{3} R^{3}=12\R^{3}=frac{12}{frac{4}{3}}=frac{12cdot 3}{4}=9\R=sqrt[3]{9}
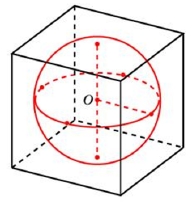
По рисунку видим, что сторона куба равна 2 радиусам:
a=2cdot sqrt[3]{9}
Объём куба:
V_{куб}=a^{3}=(2cdot sqrt[3]{9})^{3}=2^{3}cdot 9=8cdot 9=72
Ответ: 72.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 1
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Задание 8. Математика ЕГЭ. Шар вписан в куб. Найти объем куба
Рубрика Задание 8, Решаем ЕГЭ по математике Комментарии (0)
Задание. Шар, объем которого равен 36π, вписан в куб. Найдите объем куба.
Решение:
Пусть ребро куба равно a. Объем куба равен V = a^3.
Шар вписан в куб, значит, ребро куба равно двум радиусам шара: a = 2R.
Найдем радиус шара. Объем шара равен V = 4/3πR^3.
36π = 4/3πR^3;
36 = 4/3R^3;
R^3 = 27;
R = 3.
a = 6.
V = 6^3 = 216.
Ответ: 216.
Понравилось? Нажмите