В данной публикации мы рассмотрим, как можно найти объем куба и разберем примеры решения задач для закрепления материала.
- Формула вычисления объема куба
- Примеры задач
Формула вычисления объема куба
1. Через длину ребра
Объем (V) куба равняется произведению его длины на ширину на высоту. Т.к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.
V = a ⋅ a ⋅ a = a3

2. Через длину диагонали грани
Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: a=d/√2.

Следовательно, вычислить объем куба можно так:
![]()
Примеры задач
Задание 1
Вычислите объем куба, если его ребро равняется 5 см.
Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см3.
Задание 2
Известно, что объем куба равен 512 см3. Найдите длину его ребра.
Решение:
Пусть ребро куба – это a. Выведем его длину из формулы расчета объема:![]()
Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.
Решение:
Применим формулу, в которой используется диагональ грани:
![]()
Куб – это трехмерная фигура, представляющая собой правильный многогранник, все грани которого квадраты. Чтобы найти объем куба достаточно знать только длину его стороны (они у куба равны).
Чтобы найти объем куба можно воспользоваться калькулятором, либо одной из подходящих формул, которые мы приводим ниже.
Содержание:
- калькулятор объема куба
- формула объема куба через ребро
- формула объема куба через диагональ грани
- формула объема куба через периметр грани
- формула объема куба через диагональ куба
- формула объема куба через площадь полной поверхности
- примеры задач
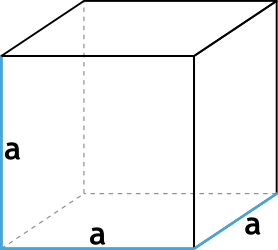
Формула объёма куба через ребро
Формула объёма куба через диагональ грани
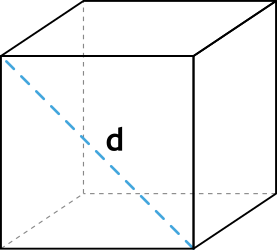
{V = Big( dfrac{d}{sqrt{2}} Big) ^3}
d – диагональ грани куба
Формула объёма куба через периметр грани
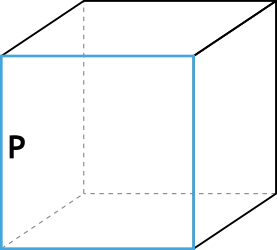
{V= Big( dfrac{P}{4} Big) ^3}
P – периметр грани куба
Формула объёма куба через диагональ куба
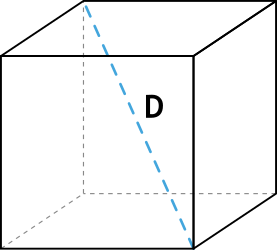
{V= dfrac{D^3}{3sqrt{3}}}
D – диагональ куба
Формула объёма куба через площадь полной поверхности
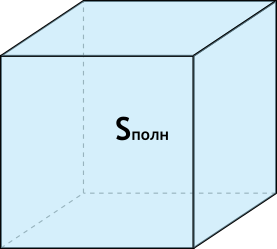
{V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}}}
Sполн – диагональ куба
Примеры задач на нахождение объема куба
Задача 1
Чему равен объём куба с ребром 5 см?
Решение
Для нахождения объема куба, когда известа длина ребра, воспользуемся первой формулой:
V=a ^ 3 = 5 ^ 3 = 125 : см^3
Ответ: 125 см³
Воспользуемся калькулятором для проверки полученного результата.
Задача 2
Найти объем куба, если площадь его поверхности равна 96 см².
Решение
В данном примере нам подойдет эта формула:
V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}} = dfrac{sqrt{{96}^3}}{6sqrt{6}} = dfrac{sqrt{96 cdot 96 cdot 96}}{6sqrt{6}} = dfrac{96 sqrt{96}}{6sqrt{6}} = dfrac{96 sqrt{16 cdot 6}}{6sqrt{6}} = dfrac{96 cdot 4 sqrt{6}}{6sqrt{6}} = dfrac{384 sqrt{6}}{6sqrt{6}} = 64 : см^3
Ответ: 64 см³
Проверить ответ поможет калькулятор .
Также на нашем сайте вы можете найти объем конуса.
Volume of a cube is defined as the total number of cubic units occupied by the cube completely. A cube is a three-dimensional solid figure, having 6 square faces. Volume is nothing but the total space occupied by an object. An object with a larger volume would occupy more space. The volume of the cube is calculated by multiplying the length, breadth, and height of the cube. For a cube the length, breadth, and height are equal. Thus, the volume of a cube is just side cube.
Let us understand the volume of a cube in detail along with the formula and solved examples in the following sections. Also, learn about the Surface area of the cube here.
What is Volume of a Cube?
Volume of a cube is defined as the total capacity of the cube it is the total amount of liquid a cube can hold. The volume of a cube is measured in cubic units such as cm3, m3, etc.
A cube is a solid 3-D figure, with 6 square faces. All the faces of a cube are square hence it has all dimensions equal
Let the length, width, and height of a cube be ‘a’, then;
Volume of cube = a × a × a
Volume of Cube = a3
All corners of a cube meet at an angle of 90° degrees. The figure below shows a cube, where l is the length, b is the width, h is the height and l = b = h. The length, width, and height represent the edges of the cube and when three edges meet at a point, it is called a vertex.

Volume of Cube Formula
Volume of a cube is defined as the total number of cube units that the cube occupies completely. A cube is a three-dimensional shape with six faces, twelve edges, and eight vertices. Therefore, the volume of a cube is the space surrounded by its six faces. Volume of the cube is calculated using two formulas which are discussed below:
Volume of Cube If Side is Given
The formula to calculate the volume of a cube when the side (Let a) of the cube is given
Volume of the cube = a × a × a
= a3
Thus, when the edge length is known volume of the cube can easily be found
Example: Find the volume of a cube with a side of 5 cm
Solution:
Given,
Edge length( a) = 5 cm
Volume = 53
= 5 x 5 x 5
= 125 cm3
Volume of a Cube If Diagonal is Given
The formula to calculate the volume of a cube when the diagonal of the cube is given
Volume of the cube = [√3 × (d)3] / 9
where
d is the diagonal of cube
Volume of a Cube Equation
The equation which gives the volume of a cube is discussed below. Suppose a cube of edge length ‘a’ is taken then its volume is calculated using the formula.
Volume of Cube(V) = a × a × a = a3
For example, what is the volume of the cube if the side length is 7 m?
Solution:
Side of cube =7 m
Volume of cube equation,
v = a3
putting the value of a in above equation we get,
v = (7)3
v = 643 m3
Thus, the volume of the cone is 643 m3
Derivation of Volume of a Cube
The volume of any object is the space occupied by that solid in the 3-D plane. In a cube all the sides i.e. length, breadth, and height are equal (l = b = h). The formula for the volume of a cube is derived as follows:
- A cube can be considered as layers of squares that are stacked on top of one another. Thus, for the base of a square shape, the area is length multiplied by its breadth.
- In a square, length, and breadth are equal, thus the area will be “a2“.
- A cube is made by adding multiple layers of square sheets on top of one other until the height becomes “a” unit. Thus, the height of the cube is “a”.
Now the volume of any regular figure is the base area multiplied by the height.
Thus,
Volume of Cube = Base Area × Height
= a2 × a = a3 units3
How to Find the Volume of a Cube?
Two methods by which the volume of a cube can be found are
- Using Edge-length
- Using Diagonal
Volume of a Cube is calculated using the steps discussed below:
Step 1: Note the dimension of the cube. Let the side is represented by (a) and the diagonal is represented as (d).
Step 2: Now use the formula,
V = a3
where
a is the length of the side of a cube,OR
V = [√3 × (d)3] / 9
where
d is the diagonal of the cube accordinglyStep 3: Simplify the above eqaution.
Step 4: Add unit3 to the answer in step 3 to the volume of the cube.
As the volume of a cube is a cubic function it increases drastically if we change the dimension of the cube. This can be understood by the following image.
.png)
Surface Area of a Cube
Surface area of the cube is the total area covered by all the faces of the cube. As a cube has six square faces of similar dimensions its volume is calculated by the formula,
Surface Area of Cube = 6a2
where,
a is the side of the cube.
Learn More, Surface Area of a Cube
Volume of a Cube and Cuboid
Cube is a three-dimensional figure with six faces and three dimensions length, breadth, and height but for a cube all the dimension length = breadth = height = a(say). Then its volume is given as,
Volume = a3
Cuboid is a three-dimensional figure with six faces and three dimensions length, breadth, and height> Leth the length, breadth, and height of the cube are l, b, and h respectively then its volume is given as,
Volume = l × b × h
Learn more, Volume of a Cuboid
Examples of Volume of a Cube from Everyday Life
Various examples which we come across in our daily life resembles cube and we are required to find their volume. Some of the common examples are,
- A cubical cardboard box is used to pack various objects.
- Some of the rooms we live in are shaped like cubes.
- An aquarium in the shape of a cube can hold water and the amount of water it can hold is calculated using the volume of cube formula, etc.
Read More
- Volume of Cone
- Volume of Sphere
- Volume of Cylinder
Solved Examples on Volume of Cube
Example 1: If the volume of a cube is 216 cm3, what is the dimension of the cube?
Solution:
Given,
The volume of a cube, V = 216 cm3
Volume of cube = (side)3
= (216)= (6)3
Therefore, the side of cube is 6 cm
Example 2: How many 3 cm × 3 cm × 3 cm cube boxes can fit in a large 15 cm cube box?
Solution:
Volume of each box = (3 × 3 × 3) cm3 = 27 cm3.
Volume of large cube box = (15 × 15 × 15) cm3 = 3375 cm3.
Number of boxes = Volume of large cube / Volume of small cube
= 3375cm3 / 27cm3
= 125 boxes
Thus, 125 boxes are required to fit in the large box.
Example 3: The volume of a cubic hard disk is 0.5 dm3. What are the dimensions of the disk?
Solution:
Since, the Volume of a cube = a3
0.5 = a3
a = 3√0.5
= 0.794 dm
Example 4: Calculate the volume of a cube with a diagonal of 3 inches.
Solution:
Given,
Diagonal = 9 inch.
Cube Volume = [√3 × (Diagonal)3] / 9
Volume = √3×[(3)3/9]
= √3 × 3
= 1.732 × 3= 5.196 inches3
Example 5: Find the edge of a cube whose volume is 1000 cm3
Solution:
Volume = 1000 cm3l
Volume = a3
where,
a is edge of the cube1000 = 103 = a3
a (edge) = 10 cm
Thus, the edge of the cube is 10 cm.
Example 6: Find the volume of a cube of side 0.01 cm
Solution:
Given,
Edge (a) = 0.01 cm
Volume = a3
Volume = (0.01)3
= 0.000001 cm3Thus, the volume of the cube is 10-6 cm3
FAQs on Volume of a Cube
Q1: What is the volume of a cube?
Answer:
Volume of a cube is defined as the total capacity of a cube. It is the total amount of liquid a cube can hold.
Q2: What is the unit of volume?
Answer:
The unit of volume is given by cubic units i.e. volume is always measured in m3, cm3, etc. It is generally measured in liters.
Q3: How to find the volume of a cube?
Answer:
The volume of the cube is calculated using the formula,
Volume = a3
where
a is the edge length of a cube
Q4: What is the volume of a cube if diagonals of the cube are given?
Answer:
The volume of a cube when diagonals are given is calculated using the formula,
Volume = [√3 × (d)3] / 9
where
d is the diagonal of a cube
Q5: How many litres are in a meter cube?
Answer:
We know that,
1 cm3 = 1 cc (cubic centimeter) = 1 ml and,
1 m3 = 1000000 cm3
1 m3 = 1000000 ml
1 m3 = 1000 litres
Thus, 1 m3 has 1000 litres
Q6: What is the volume of a cube of side 2a?
Answer:
The formula for the volume of a cube is
Volume = (side)3
Now if the side is 2a then its volume is,
Volume = (2a)3
= 8a3
Thus, the volume of the cube with side 2a is 8a3
Загрузить PDF
Загрузить PDF
Куб — трехмерная геометрическая фигура, у которой все ребра равны (длина равна ширине и равна высоте). У куба шесть квадратных граней, которые пересекаются под прямым углом и стороны которых равны. Вычислить объем куба легко — нужно перемножить длину, ширину и высоту. Так как у куба длина равна ширине и равна высоте, то объем куба равен s3, где s — длина одного (любого) ребра куба.
-

1
Найдите длину одного ребра куба. Как правило, длина ребра куба дана в условии задачи. Если вы вычисляете объем реального объекта кубической формы, измерьте его ребро линейкой или рулеткой.
- Рассмотрим пример. Ребро куба равно 5 см. Найдите объем куба.
-

2
Возведите в куб длину ребра куба. Другими словами, умножьте длину ребра куба саму на себя три раза. Если s — длина ребра куба, то s * s *s = s3 и, таким образом, вы вычислите объем куба.
- Этот процесс аналогичен процессу нахождения площади основания куба (равна произведению длины на ширину квадрата в основании) и последующему умножению площади основания на высоту куба (то есть, другими словами, вы умножаете длину на ширину и на высоту). Так как в кубе длина ребра равна ширине и равна высоте, то этот процесс можно заменить возведением ребра куба в третью степень.
- В нашем примере объем куба равен 5 * 5 *5 = 53 = 125.
-

3
К ответу припишите единицы измерения объема (если вы этого не сделаете, ваша оценка может быть снижена). Так как объем — это количественная характеристика пространства, занимаемого телом, то единицами измерения объема являются кубические единицы (кубические сантиметры, кубические метры и так далее).
- В нашем примере размер ребра куба давался в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах (или в см3). Итак, объем куба равен 125 см3.
- Если размер ребра куба дается в других единицах, то и объем куба измеряется в соответствующих кубических единицах. Например, если ребро куба равно 5 м (а не 5 см), то его объем равен 125 м3.
Реклама
-

1
В некоторых задачах длина ребра куба не дана, но даны другие величины, с помощью которых можно найти ребро куба и его объем. Например, если вам дана площадь поверхности куба, то разделите ее на 6, из полученного значения извлеките квадратный корень и вы найдете длину ребра куба. Затем возведите длину ребра куба в третью степень и вычислите объем куба.
- Площадь поверхности куба равна 6s2, где s — длина ребра куба (то есть вы находите площадь одной грани куба, а затем умножаете ее на 6, так как у куба 6 равных граней).
- Рассмотрим пример. Площадь поверхности куба равна 50 см2. Найдите объем куба.
-

2
Разделите площадь поверхности куба на 6 (так как у куба 6 равных граней, вы получите площадь одной грани куба). В свою очередь площадь одной грани куба равна s2, где s — длина ребра куба.
- В нашем примере: 50/6 = 8,33 см2 (не забывайте, что площадь измеряется в квадратных единицах — см2, м2 и так далее).
-

3
Так как площадь одной грани куба равна s2, то извлеките квадратный корень из значения площади одной грани и получите длину ребра куба.
- В нашем примере, √8,33 = 2,89 см.
-

4
Возведите в куб полученное значение, чтобы найти объем куба (как описано в предыдущем разделе).
- В нашем примере: 2,89 * 2,89 * 2,89 = 2,893 = 24,14 см3. К ответу не забудьте приписать кубические единицы.
Реклама
-

1
Разделите диагональ одной из граней куба на √2, чтобы найти длину ребра куба. Таким образом, если в задаче дана диагональ грани (любой) куба, то вы можете найти длину ребра куба, разделив диагональ на √2.
- Рассмотрим пример. Диагональ грани куба равна 7 см. Найдите объем куба. В этом случае длина ребра куба равна 7/√2 = 4,96 см. Объем куба равен 4,963 = 122,36 см3.
- Запомните: d2 = 2s2, где d — диагональ грани куба, s — ребро куба. Эта формула вытекает из теоремы Пифагора, согласно которой квадрат гипотенузы (в нашем случае диагональ грани куба) прямоугольного треугольника равен сумме квадратов катетов (в нашем случае ребер), то есть d2 = s2 + s2 = 2s2.
-

2
Разделите диагональ куба на √3, чтобы найти длину ребра куба. Таким образом, если в задаче дана диагональ куба, то вы можете найти длину ребра куба, разделив диагональ на √3. Диагональ куба — отрезок, соединяющий две вершины, симметричные относительно центра куба, равный D2 = 3s2 (где D — диагональ куба, s — ребро куба).
- Эта формула вытекает из теоремы Пифагора, согласно которой квадрат гипотенузы (в нашем случае диагональ куба) прямоугольного треугольника равен сумме квадратов катетов (в нашем случае один катет — это ребро, а второй катет — это диагональ грани куба, равная 2s2), то есть D2 = s2 + 2s2 = 3s2.
- Рассмотрим пример. Диагональ куба равна 10 м. Найдем объем куба:
- D2 = 3s2
- 102 = 3s2
- 100 = 3s2
- 33,33 = s2
- 5,77 м = s
- Объем куба равен 5,773 = 192,45 м3
Реклама
Об этой статье
Эту страницу просматривали 605 106 раз.
Была ли эта статья полезной?
Куб (или гексаэдр) — это правильный многогранник, который состоит из многоугольников, являющихся квадратами.
У куба 12 ребер – отрезков, которые являются сторонами квадратов (граней куба).
Также он имеет 8 вершин и 6 граней.
Онлайн-калькулятор объема куба
Формула объема куба
Для нахождения объема куба нужно перемножить его измерения – длину, ширину и высоту. Исходя из того, что куб состоит из квадратов, все его измерения одинаковы и численно равны длине ребра.
Формула для вычисления объема куба такова:
V=a3V=a^3
где aa — длина ребра куба.
Рассмотрим несколько примеров.
Найти объем куба, если периметр PP его грани aa равен 16 cм.16text{ cм.}
Решение
P=16P=16
Периметр PP грани куба связан с длиной его ребра aa по формуле:
P=a+a+a+a=4⋅aP=a+a+a+a=4cdot a
16=4⋅a16=4cdot a
a=164=4a=frac{16}{4}=4
Найдем объем нашего тела:
V=a3=43=64 см3V=a^3=4^3=64text{ см}^3
Ответ: 64 см3.64text{ см}^3.
Одна четвертая часть диагонали квадрата равна 3 см.3text{ см.} Найти объем куба, образованного данным четырехугольником.
Решение
Пусть dd — диагональ фигуры, тогда по условию:
d4=3frac{d}{4}=3
d=4⋅3=12d=4cdot 3=12
Найдем сторону этого квадрата. Обратимся за помощью к теореме Пифагора:
a2+a2=12a^2+a^2=12,
где aa — сторона квадрата.
2⋅a2=122cdot a^2=12
a=6a=sqrt{6}
Приходим к окончательным расчетам для объема:
V=a3=(6)3=66 см3V=a^3=(sqrt{6})^3=6sqrt{6}text{ см}^3
Ответ: 66 см3.6sqrt{6}text{ см}^3.
Чуть более сложный пример.
В куб вписан шар, площадь SS которого равна 64π64pi. Найти объем куба.
Решение
S=64πS=64pi
Первый шагом является нахождение радиуса RR данного шара. Формула его площади такова:
S=4⋅π⋅R2S=4cdotpicdot R^2
64π=4⋅π⋅R264pi=4cdotpicdot R^2
64=4⋅R264=4cdot R^2
644=R2frac{64}{4}=R^2
16=R216=R^2
R=4R=4
Для куба радиус вписанного шара является половиной его стороны aa:
a=2⋅R=2⋅4=8a=2cdot R=2cdot4=8
Объем вычисляется следующим образом:
V=a3=83=512 см3V=a^3=8^3=512text{ см}^3
Ответ: 512 см3.512text{ см}^3.
На Студворке вы можете оформить заказ контрольных работ для студентов по самым низким ценам!
