В данной публикации мы рассмотрим, как можно найти объем куба и разберем примеры решения задач для закрепления материала.
- Формула вычисления объема куба
- Примеры задач
Формула вычисления объема куба
1. Через длину ребра
Объем (V) куба равняется произведению его длины на ширину на высоту. Т.к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.
V = a ⋅ a ⋅ a = a3

2. Через длину диагонали грани
Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: a=d/√2.

Следовательно, вычислить объем куба можно так:
![]()
Примеры задач
Задание 1
Вычислите объем куба, если его ребро равняется 5 см.
Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см3.
Задание 2
Известно, что объем куба равен 512 см3. Найдите длину его ребра.
Решение:
Пусть ребро куба – это a. Выведем его длину из формулы расчета объема:![]()
Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.
Решение:
Применим формулу, в которой используется диагональ грани:
![]()
Куб – это трехмерная фигура, представляющая собой правильный многогранник, все грани которого квадраты. Чтобы найти объем куба достаточно знать только длину его стороны (они у куба равны).
Чтобы найти объем куба можно воспользоваться калькулятором, либо одной из подходящих формул, которые мы приводим ниже.
Содержание:
- калькулятор объема куба
- формула объема куба через ребро
- формула объема куба через диагональ грани
- формула объема куба через периметр грани
- формула объема куба через диагональ куба
- формула объема куба через площадь полной поверхности
- примеры задач
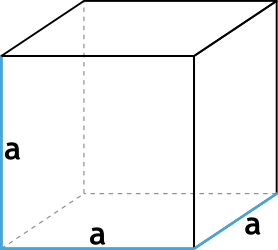
Формула объёма куба через ребро
Формула объёма куба через диагональ грани
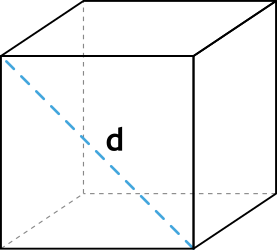
{V = Big( dfrac{d}{sqrt{2}} Big) ^3}
d – диагональ грани куба
Формула объёма куба через периметр грани
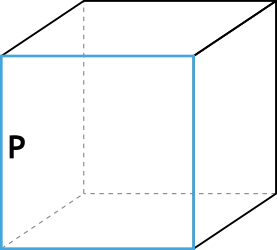
{V= Big( dfrac{P}{4} Big) ^3}
P – периметр грани куба
Формула объёма куба через диагональ куба
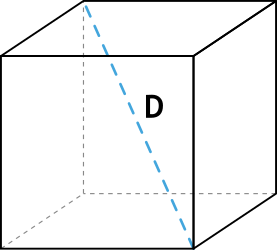
{V= dfrac{D^3}{3sqrt{3}}}
D – диагональ куба
Формула объёма куба через площадь полной поверхности
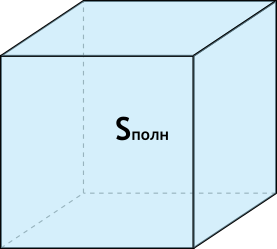
{V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}}}
Sполн – диагональ куба
Примеры задач на нахождение объема куба
Задача 1
Чему равен объём куба с ребром 5 см?
Решение
Для нахождения объема куба, когда известа длина ребра, воспользуемся первой формулой:
V=a ^ 3 = 5 ^ 3 = 125 : см^3
Ответ: 125 см³
Воспользуемся калькулятором для проверки полученного результата.
Задача 2
Найти объем куба, если площадь его поверхности равна 96 см².
Решение
В данном примере нам подойдет эта формула:
V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}} = dfrac{sqrt{{96}^3}}{6sqrt{6}} = dfrac{sqrt{96 cdot 96 cdot 96}}{6sqrt{6}} = dfrac{96 sqrt{96}}{6sqrt{6}} = dfrac{96 sqrt{16 cdot 6}}{6sqrt{6}} = dfrac{96 cdot 4 sqrt{6}}{6sqrt{6}} = dfrac{384 sqrt{6}}{6sqrt{6}} = 64 : см^3
Ответ: 64 см³
Проверить ответ поможет калькулятор .
Также на нашем сайте вы можете найти объем конуса.
Объём куба
- Главная
- /
- Математика
- /
- Геометрия
- /
- Объём куба
Чтобы найти объём куба воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Объём куба через ребро
Чему равен объём куба, если:
ребро a =
Vкуба =
0
Округление ответа:
Объём куба через диагональ
Чему равен объём куба, если:
диагональ d =
Vкуба =
0
Округление ответа:
Объём куба через площадь поверхности
Чему равен объём куба, если:
Sпов =
Vкуба =
0
Округление ответа:
Теория
Как найти объём куба зная длину ребра
Чему равен объём куба Vкуба, если длина его рёбер a:
Формула
Vкуба = a³
Пример
Для примера, найдём объём куба, у которого рёбра a = 5 см:
Vкуба = 5³ = 125 см³
Как найти объём куба зная диагональ
Чему равен объём куба Vкуба, если его диагональ d:
Формула
Vкуба = d³ ⁄3√3
Пример
Для примера, найдём объём куба, длина диагонали которого d = 9 см:
Vкуба = 9³ / 3√3 ≈ 729 / 5,2 ≈ 140 см³
Как найти объём куба зная площадь поверхности
Чему равен объём куба Vкуба, если площадь поверхности этого куба Sпов:
Формула
Vкуба = √Sпов³ ⁄6√6
Пример
Для примера, найдём объём куба, площадь поверхности которого Sпов = 24 см²:
Vкуба = √24³ / 6√6 = 24√24 / 6√6 = 4√4 = 8 см³
См. также
Формула объема куба:
V = a3 1 см3
4,2 K
Положить кубик с ребром 1 см в градуированный стакан, налить воды, записать занятый объём по риске, до которой… Читать дальше
Комментировать ответ…Комментировать…
Постигший работу в “ООО Яндекс”, копирайтер, испытатель авиационных приборов и зародыш… · 14 мар 2019
Все довольно просто. Объем = длина*ширина*высота. Ребро куба – это и есть его сторона, а все стороны в кубе равны. Следовательно, V= 1*1*1 = 1 кубический см.
13,4 K
а вы что учитель
а вы что Читать дальше
Комментировать ответ…Комментировать…
Куб (или гексаэдр) — это правильный многогранник, который состоит из многоугольников, являющихся квадратами.
У куба 12 ребер – отрезков, которые являются сторонами квадратов (граней куба).
Также он имеет 8 вершин и 6 граней.
Онлайн-калькулятор объема куба
Формула объема куба
Для нахождения объема куба нужно перемножить его измерения – длину, ширину и высоту. Исходя из того, что куб состоит из квадратов, все его измерения одинаковы и численно равны длине ребра.
Формула для вычисления объема куба такова:
V=a3V=a^3
где aa — длина ребра куба.
Рассмотрим несколько примеров.
Найти объем куба, если периметр PP его грани aa равен 16 cм.16text{ cм.}
Решение
P=16P=16
Периметр PP грани куба связан с длиной его ребра aa по формуле:
P=a+a+a+a=4⋅aP=a+a+a+a=4cdot a
16=4⋅a16=4cdot a
a=164=4a=frac{16}{4}=4
Найдем объем нашего тела:
V=a3=43=64 см3V=a^3=4^3=64text{ см}^3
Ответ: 64 см3.64text{ см}^3.
Одна четвертая часть диагонали квадрата равна 3 см.3text{ см.} Найти объем куба, образованного данным четырехугольником.
Решение
Пусть dd — диагональ фигуры, тогда по условию:
d4=3frac{d}{4}=3
d=4⋅3=12d=4cdot 3=12
Найдем сторону этого квадрата. Обратимся за помощью к теореме Пифагора:
a2+a2=12a^2+a^2=12,
где aa — сторона квадрата.
2⋅a2=122cdot a^2=12
a=6a=sqrt{6}
Приходим к окончательным расчетам для объема:
V=a3=(6)3=66 см3V=a^3=(sqrt{6})^3=6sqrt{6}text{ см}^3
Ответ: 66 см3.6sqrt{6}text{ см}^3.
Чуть более сложный пример.
В куб вписан шар, площадь SS которого равна 64π64pi. Найти объем куба.
Решение
S=64πS=64pi
Первый шагом является нахождение радиуса RR данного шара. Формула его площади такова:
S=4⋅π⋅R2S=4cdotpicdot R^2
64π=4⋅π⋅R264pi=4cdotpicdot R^2
64=4⋅R264=4cdot R^2
644=R2frac{64}{4}=R^2
16=R216=R^2
R=4R=4
Для куба радиус вписанного шара является половиной его стороны aa:
a=2⋅R=2⋅4=8a=2cdot R=2cdot4=8
Объем вычисляется следующим образом:
V=a3=83=512 см3V=a^3=8^3=512text{ см}^3
Ответ: 512 см3.512text{ см}^3.
На Студворке вы можете оформить заказ контрольных работ для студентов по самым низким ценам!
