Задание № 4713
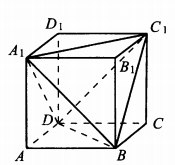
Дан куб ABCDA1B1C1D1. Объём треугольной пирамиды A1BC1D равен 3. Чему равен объём куба?
Показать ответ
Комментарий:
Объем куба проще всего посчитать, как сумму объемов данной пирамида и объемов отсеченных пирамид.
[math]V_{куб}=V_{пир}+V_{ABDA_1}+V_{BCDC_1}+V_{A_1D_1C_1D}+V_{A_1B_1C_1B}[/math]
Объемы отсеченных пирамид равны между собой и каждый из них равен шестой части объема куба (кому интересно доказательство основано на том, что основание пирамиды в 2 раза меньше основания куба, что объем пирамиды это треть произведения высоты на основание)
[math]begin{array}{l}V_{куб}=V_{пир}+4V_{отсеч}=V_{пир}+4timesfrac16V_{куб}\V_{куб}-frac23V_{куб}=V_{пир}\V_{пир}=frac13V_{куб}end{array}[/math]
Vкуб=3х3=9
Ответ: 9
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.
reang647
Вопрос по математике:
ABCDA1B1C1D1 – куб. Объем пирамиды CAA1B1B равен 72 см. Найдите объем куба
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок – бесплатно!
Ответы и объяснения 1
mairyo
Объем пирамиды вычисляется по формуле
1/3*Sосн*h
При этом высота данной пирамиды равна высоте куба, а площадь основания пирамиды равна площади основания (любой стороны) куба.
Получается, что объем куба отличается от данного объема пирамиды только коэфициентом 13, значит объем куба просто в 3 раза больше, чем объем пирамиды.
72*3=216 см

Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат – это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Математика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи –
смело задавайте вопросы!
Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.
Как найти объем куба, призмы и пирамиды
Автор:
Peter Berry
Дата создания:
16 Август 2021
Дата обновления:
6 Май 2023

Содержание
- Как найти объем куба
- Как найти объем призмы
- Как найти объем пирамиды
- Как найти объем куба, призмы и пирамиды – метод
- Как найти объем Куба, Призмы и Пирамиды – Примеры
Поскольку куб, призма и пирамида являются тремя основными твердотельными объектами в геометрии, необходимо знать, как найти объем куба, призмы и пирамиды. В математике, физических науках и технике свойства этих объектов имеют большое значение. В большинстве случаев геометрические и физические свойства более сложного объекта всегда аппроксимируются с использованием свойств твердых объектов. Объем является одним из таких свойств.
Как найти объем куба
Куб представляет собой твердый объект с шестью квадратными гранями, которые встречаются под прямым углом. Он имеет 8 вершин и 12 ребер, а его ребра равны по длине. Объем куба – это фундаментальный (возможно, самый простой для определения объем) объем всех твердых объектов. Объем куба определяется как:
Вкуб= а3, где длина его ребер.

Как найти объем призмы
Призма – это многогранник; это твердый объект, состоящий из двух конгруэнтных (похожих по форме и равных по размеру) многоугольных граней с одинаковыми краями, соединенными прямоугольниками. Многоугольная грань известна как основание призмы, а две базы параллельны друг другу. Однако не обязательно, чтобы они были точно расположены над другим. Если они расположены точно друг над другом, то прямоугольные стороны и основание встречаются под прямым углом. Этот вид призмы известен как прямоугольная призма.
Если площадь основания (многоугольной грани) равна A, а перпендикулярная высота между основаниями равна h, то объем призмы определяется по формуле:
Впризма= Ах

Результат остается верным, является ли это прямой призмой или нет.
Как найти объем пирамиды
Пирамида также является многогранником с многоугольным основанием и точкой (называемой вершиной), соединенной треугольниками, идущими от краев. У пирамиды есть только одна вершина, но количество вершин зависит от полигонального основания.
Объем пирамиды с базовой площадью A и перпендикулярной высотой к вершине h определяется как:
Впирамида= 1/3 Ач
Как найти объем куба, призмы и пирамиды – метод
Объем Куба
Куб – самый легкий твердый объект, чтобы найти объем.
- Найти длину одной стороны (рассмотрим)
- Увеличьте это значение до степени 3, т.е.3 (найти куб)
- Результирующее значение – это объем куба.
Единицей объема является куб единицы измерения, в которой была измерена длина. Поэтому, если стороны были измерены в метрах, объем дается в кубических метрах.
Объем призмы
- Найдите площадь любого основания призмы (A) и определите перпендикулярную высоту между двумя основаниями (h).
- Произведение площади h на перпендикулярную высоту дает объем призмы.
Примечание. Этот результат действителен для любого типа призмы, обычной или нерегулярной.
Объем Пирамиды
- Найдите площадь основания пирамиды (A) и определите перпендикулярную высоту от основания до вершины (h).
- Возьмите произведение площади основания и перпендикулярной высоты. Одна треть полученных значений – это объем пирамиды.
Примечание. Этот результат действителен для любого типа призмы, обычной или нерегулярной.
Как найти объем Куба, Призмы и Пирамиды – Примеры
Найти объем куба
1. Край куба имеет длину 1,5 метра. Найдите объем куба.
- Длина куба составляет 1,5 метра. Если не дано напрямую, найдите длину, используя другие геометрические средства или измерения.
- Возьмите третью степень длины. То есть (1.5)3= 1,5 × 1,5 × 1,5 = 3.375m3
- Куб имеет объем 3,375 куб.
Найти объем призмы
2. Треугольная призма имеет длину 20см. Основание призмы – равнобедренный треугольник с равными сторонами, образующий угол 600, Если длина стороны, противоположной углу, составляет 4 см, найдите объем пирамиды.
- Сначала определим площадь основания. По тригонометрическим соотношениям мы можем определить перпендикулярную высоту базового треугольника от края 4 см до противоположной вершины как 2 tan 600 = 2 × √3≅3.4641 см Следовательно, площадь основания составляет 1/2 × 4 × 3,4641 = 6,9298 см.2
- Высота перпендикуляра (как длина) составляет 20см. Теперь мы можем рассчитать объем путем умножения площади основания на перпендикулярную высоту, например, Vпризма= А × ч = 6.9298cm2× 20 см = 138.596cm3.
- Объем пирамиды 138,596 см.3.
Найти объем пирамиды
3. Прямоугольная правая пирамида имеет основание шириной 40 м и длиной 60 м. Если высота до вершины пирамиды от основания составляет 20 м, найдите объем, окруженный поверхностью пирамиды.
- Площадь основания может быть просто определена, взяв произведение длин двух сторон. Следовательно, площадь основания составляет 40 х 60 м = 2400 м.2
- Высота перпендикуляра равна 20м. Следовательно, объем пирамиды равен Vпирамида= 1/3 × 2400m2× 20m = 16,000m3

a – сторона куба
Формула объема куба, (V):


a, b, c – стороны параллелепипеда
Еще иногда сторону параллелепипеда, называют ребром.
Формула объема параллелепипеда, (V):
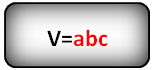

R – радиус шара
π ≈ 3.14
По формуле, если дан радиус, можно найти объема шара, (V):

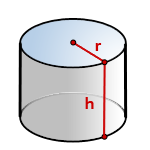
h – высота цилиндра
r – радиус основания
π ≈ 3.14
По формуле найти объема цилиндра, есди известны – его радиус основания и высота, (V):

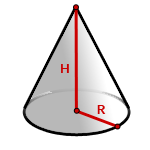
R – радиус основания
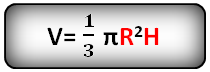
H – высота конуса
π ≈ 3.14
Формула объема конуса, если известны радиус и высота (V):
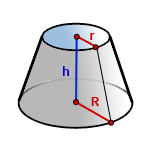
r – радиус верхнего основания
R – радиус нижнего основания
h – высота конуса
π ≈ 3.14
Формула объема усеченного конуса, если известны – радиус нижнего основания, радиус верхнего основания и высота конуса (V ):

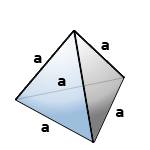
Правильный тетраэдр – пирамида у которой все грани, равносторонние треугольники.
а – ребро тетраэдра
Формула, для расчета объема правильного тетраэдра (V):
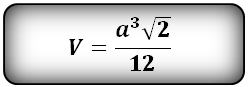
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
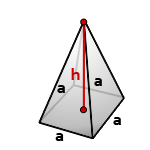
a – сторона основания
h – высота пирамиды
Формула для вычисления объема правильной четырехугольной пирамиды, (V):
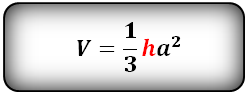
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
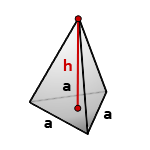
a – сторона основания
h – высота пирамиды
Формула объема правильной треугольной пирамиды, если даны – высота и сторона основания (V):

Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
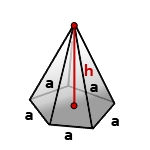
h – высота пирамиды
a – сторона основания пирамиды
n – количество сторон многоугольника в основании
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):
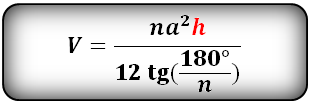
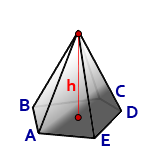
h – высота пирамиды
S – площадь основания ABCDE
Формула для вычисления объема пирамиды, если даны – высота и площадь основания (V):
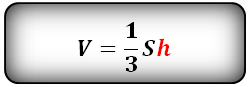
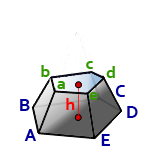
h – высота пирамиды
Sниж – площадь нижнего основания, ABCDE
Sверх – площадь верхнего основания, abcde
Формула объема усеченной пирамиды, (V):

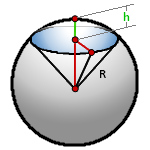
Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.

R – радиус шара
h – высота сегмента
π ≈ 3.14
Формула для расчета объема шарового сегмента, (V):
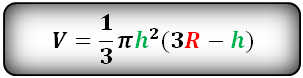
R – радиус шара
h – высота сегмента
π ≈ 3.14
Формула объема шарового сектора, (V):

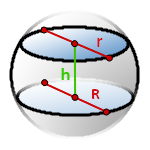
h – высота шарового слоя
R – радиус нижнего основания
r – радиус верхнего основания
π ≈ 3.14
Формула объема шарового слоя, (V):
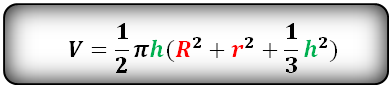
Куб – это трехмерная фигура, представляющая собой правильный многогранник, все грани которого квадраты. Чтобы найти объем куба достаточно знать только длину его стороны (они у куба равны).
Чтобы найти объем куба можно воспользоваться калькулятором, либо одной из подходящих формул, которые мы приводим ниже.
Содержание:
- калькулятор объема куба
- формула объема куба через ребро
- формула объема куба через диагональ грани
- формула объема куба через периметр грани
- формула объема куба через диагональ куба
- формула объема куба через площадь полной поверхности
- примеры задач
Формула объёма куба через ребро
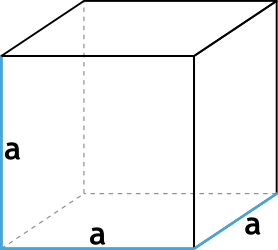
Формула объёма куба через диагональ грани
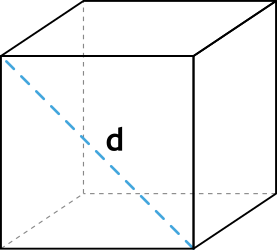
{V = Big( dfrac{d}{sqrt{2}} Big) ^3}
d – диагональ грани куба
Формула объёма куба через периметр грани
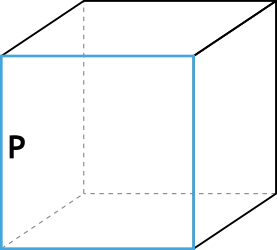
{V= Big( dfrac{P}{4} Big) ^3}
P – периметр грани куба
Формула объёма куба через диагональ куба
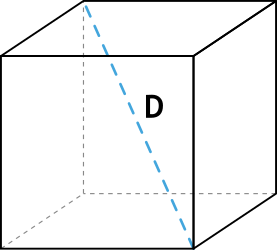
{V= dfrac{D^3}{3sqrt{3}}}
D – диагональ куба
Формула объёма куба через площадь полной поверхности
{V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}}}
Sполн – диагональ куба
Примеры задач на нахождение объема куба
Задача 1
Чему равен объём куба с ребром 5 см?
Решение
Для нахождения объема куба, когда известа длина ребра, воспользуемся первой формулой:
V=a ^ 3 = 5 ^ 3 = 125 : см^3
Ответ: 125 см³
Воспользуемся калькулятором для проверки полученного результата.
Задача 2
Найти объем куба, если площадь его поверхности равна 96 см².
Решение
В данном примере нам подойдет эта формула:
V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}} = dfrac{sqrt{{96}^3}}{6sqrt{6}} = dfrac{sqrt{96 cdot 96 cdot 96}}{6sqrt{6}} = dfrac{96 sqrt{96}}{6sqrt{6}} = dfrac{96 sqrt{16 cdot 6}}{6sqrt{6}} = dfrac{96 cdot 4 sqrt{6}}{6sqrt{6}} = dfrac{384 sqrt{6}}{6sqrt{6}} = 64 : см^3
Ответ: 64 см³
Проверить ответ поможет калькулятор .
Также на нашем сайте вы можете найти объем конуса.
