Как найти обьем квадрата по его ребрам

Как найти объём квадрата

Очень часто школьники делают запросы в поисковой системе: как найти объем квадрата. Ответ может быть только один: это невозможно. Квадрат – двумерная фигура (два параметра: длина и ширина). Для вычисления объема необходимо наличие третьей характеристики: высоты. Возможно, имеется ввиду вычисление площади квадрата, его периметра или вычисление объема и площади поверхности куба.

Инструкция

Квадрат – равносторонний четырехугольник, в котором каждый угол равен 90°. Чтобы найти площадь (S) нужно умножить его длину (l) на ширину (b). Так как в этой фигуре длина и ширина равны, то достаточно знать одну из величин. Единицы измерения площади: см?, м?, км? и т.д.Например: длина одной стороны квадрата = 5 см. Нужно вычислить площадь. Найдите ее по формуле: S = l * b.
S = 5см * 5см.
S = 25см?.
Ответ: площадь квадрата со стороной 5 см равна 25 см?.

Куб – многогранник, в котором каждая грань – квадрат. Куб имеет двенадцать ребер, которые равны друг другу (т.е длина, ширина и высота одной грани – это длина (высота) ребра) и шесть одинаковых сторон. Чтобы найти объем куба, необходимо перемножить три его ребра (а). Единицы измерения объема: см?, дм?, м? и т.п.Например: длина ребра 5 см. Нужно найти объем куба. Рассчитайте по формуле:
V = а * а * а или V = a?.
V = 5см * 5см * 5 см.
V = 125 см?
Ответ: объем куба с длиной ребра 5 см равен 125 см?.

Если необходимо вычислить площадь всех сторон куба, то сначала найдите площадь одной стороны, а потом суммируйте площади всех шести сторон. Например: известно, что длина одной грани куба 5 см. Нужно найти площадь его поверхности. Решение имеет вид :
1. S = 5см*5 см = 25см?
2. ? = S+ S+ S+ S+ S+ S или S? =6*S
S?= 6*25см? = 150см?
Ответ: площадь поверхности куба с длиной ребра 5 см – 150см?Если требуется найти одну из геометрических характеристик, зная объем куба или площадь квадрата, то из значения объема извлекается кубический корень, а из значения площади – квадратный.

Периметр квадрата представляет собой сумму длин всех сторон. Т.е. нужно сложить значения четырех его длин.Например: длина квадрата 5 см. Вычислите периметр. Для вычисления периметра любого прямоугольника можно воспользоваться формулой: P = 2*(l+b).
Для квадрата формула имеет упрощенный вид: P = 4*l
P = 4*5см = 20см
Ответ: периметр квадрата длиной 5см – 20см.

Источники:

• формула объёма квадрата

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Целый круг в интерьере встречается достаточно редко. Полностью круглым может быть окно, колонны, центральная часть многоуровневого потолка. В основном дело приходится иметь с частями круга: половиной или сегментами.

Рулеткой снимают размер между двумя противоположными точками круга. Этот отрезок будет называться

диаметром. Радиус круга равен половине диаметра.

Подсчёт площади круга производят по формуле S = π*R², где:

• R – радиус;
• S – площадь круга;
• π – постоянная математическая величина, округлённая до значения 3,14.

Числовое значение площади полукруга получают делением полученного результата на 2.

Квадратура сектора круга равна произведению половины длины дуги сектора на радиус круга, вычисляется по формуле S = 1/2 L*R.

Треугольник

Формула площади треугольника S=1/2*Н*А, где:

• S – площадь треугольника;
• Н – высота;
• А – сторона треугольника.

Высоту треугольника получают, измеряя рулеткой перпендикуляр от угла, противоположного к стороне.

Посмотрите на видео ниже полезные советы для быстрого и правильного подсчета квадратуры стен и пола:

Используя простые формулы из школьного курса геометрии, можно подсчитать любую нужную величину для строительства или ремонта.

Статья полезна? Сохраните закладку или отметьте для друзей!

domavlad.ru

Как найти объем через площадь 🚩 как найти высоту куба 🚩 Математика

4 октября 2011

Автор КакПросто!

Объем – мера вместимости, выраженная для геометрических фигур в виде формулы V=l*b*h. Где l – длина, b – ширина, h – высота объекта. При наличии только одной или двух характеристик вычислить объем в большинстве случаев нельзя. Однако при некоторых условиях представляется возможным сделать это через площадь.

Статьи по теме:

Инструкция

Задача первая: вычислить объем, зная высоту и площадь. Это самая простая задача, т.к. площадь (S) — это произведение длинны и ширины (S= l*b), а объем – произведение длины, ширины и высоты. Подставьте в формулу вычисления объема вместо l*b площадь. Вы получите выражение V=S*h.Пример: Площадь одной из сторон параллелепипеда — 36 см², высота – 10 см. Найдите объем параллелепипеда.V = 36 см² * 10 см = 360 см³.Ответ: Объем параллелепипеда равен 360 см³. Задача вторая: вычислить объем, зная только площадь. Это возможно, если вы вычисляете объем куба, зная площадь одной из его граней. Т.к. ребра куба равны, то извлекая из значения площади квадратный корень, вы получите длину одного ребра. Эта длина будет и высотой, и шириной.Пример: площадь одной грани куба — 36 см². Вычислите объем.Извлеките квадратный корень из 36 см². Вы получили длину – 6 см. Для куба формула будет иметь вид: V = a³, где а – ребро куба. Или V = S*a, где S – площадь одной стороны, а – ребро (высота) куба.V = 36 см² * 6 см = 216 см³. Или V = 6³см = 216 см³.Ответ: Объем куба равен 216 см³.

Задача третья: вычислить объем, если известна площадь и некоторые другие условия. Условия могут быть разные, помимо площади могут быть известны другие параметры. Длина или ширина могут быть равны высоте, больше или меньше высоты в несколько раз. Также могут даваться дополнительные сведения о фигурах, которые помогут в вычислениях объема.Пример 1: найдите объем призмы, если известно, что площадь одной стороны 60 см², длина 10 см, а высота равна ширине.S = l * b; l = S : b
l = 60 см² : 10 см = 6 см – ширина призмы. Т.к. ширина равна высоте, вычислите объем:
V=l*b*h
V = 10 см * 6 см *6 см = 360 см³Ответ:объем призмы 360 см³

Пример 2: найдите объем фигуры, если площадь 28 см², длина фигуры 7 см. Дополнительное условие: четыре стороны равны между собой, и соединены друг с другом по ширине.Для решения следует построить параллелепипед. l = S : b
l = 28 см² : 7 см = 4 см – ширинаКаждая сторона представляет собой прямоугольник, длина которого 7 см, а ширина 4 см. Если четыре таких прямоугольника соединить между собой по ширине, то получится параллелепипед. Длина и ширина в нем по 7 см, а высота 4 см. V = 7 см * 7 см * 4 см = 196 см³Ответ: Объем параллелепипеда = 196 см³.

Человек, покупая новую квартиру, обычно мало интересуется ее объемом. Его куда больше интересует площадь. Знать площадь необходимо и для расстановки мебели, и для расчета коммунальных площадей. Но наступает момент, когда владелец квартиры хочет купить кондиционер и задает себе вопрос, какая у столь необходимого ему прибора должна быть мощность. Мощность же рассчитывается от объема помещения. Рассчитать объем помещений может понадобиться и при проектировании детских и общественных учреждений, когда на каждого посетителя по санитарным нормам должно приходиться определенное количество кубометров воздуха.

Вам понадобится

• Рулетка
• Уровень
• Стремянка

Инструкция

Чтобы рассчитать объем помещения прямоугольной формы, никаких особых ухищрений не требуется. Достаточно замерить и перемножить длину, ширину и высоту. Единственное, о чем безусловно следует позаботиться — о точности измерений. Инструмент должен быть поверен. Лучше перед замерами провести на стене строго вертикальную и строго горизонтальную линии, потому что если мерить длину по плинтусу, можно получить ошибку. Линии можно провести с помощью уровня и металлического угольника. Следите, чтобы начало линии точно совпало с нулевой отметкой рулетки. Если помещение имеет выступы, ниши, вентиляционный короб и прочие объекты, необходимо поделить его на зоны. В помещении с нишей проведите по полу прямую линию, отсекающую нишу. Замерьте сначала параметры большей части помещения и вычислите объем. Затем точно так же замерьте нишу, перемножьте мерки и приплюсуйте получившийся объем к объему другого помещения. Если основная часть комнаты и ниша одной высоты, то вертикальную мерку второй раз снимать, конечно же, нет смысла. Если же высота разная, то придется это сделать.

Если в комнате есть, например, антресоль или вентиляционный короб, которые «съедают» часть объема, необходимо измерить и их. Делается это точно так же, как измерение помещения, только получившееся число надо вычесть из общего объема помещения.

Несколько больше проблем может возникнуть с помещением непрямоугольной формы. Если вам нужно вычислить объем круглой веранды или мансарды, постарайтесь максимально точно вычислить площадь пола. Найдите центр, проведите через него несколько радиусов и замерьте один из них. Для поверки можно замерить все радиусы, они должны быть одинаковыми. Пол веранды трапециевидной формы разделите прямыми линиями на прямоугольник и 2 треугольника. Так будет гораздо удобнее вычислять площадь, нежели вспоминать формулу площади трапеции. Сложите вместе площади прямоугольника и треугольников и умножьте все это на высоту помещения.

Полезный совет

Замеры удобнее производить вдвоем.

Определение строительных объемов необходимо для вычисления стоимости проекта. Ведомость по подсчету объемов работ — это главный документ при определении сметной стоимости всего строительства. Так как же посчитать строительный объем?

Инструкция

Для составления ведомостей объемов работ используют нормативные документы, а также технические справочники, указания и другие технические документы. Подсчеты работ рекомендуется организовывать по проверенным схемам, которые наглядно представляют сам ход расчетов, а также полностью последовательность их производства. Для этого подойдут определенные правила. Строительный объем подвала определяйте, умножая площадь сечения подвала по горизонтали на уровне нижнего этажа, замеряя выше цоколя на высоту от уровня пола до такого же уровня пола с нижнего этажа. Если подвал возведен внутри здания без устройства стен над ним, площадь высчитывайте по внешней обводке стен на уровне перекрытия над подвалом. Строительный объем верхней, наземной части дома с чердачным перекрытием определяйте, умножая площадь горизонтального сечения по внешней обводке строения (учитывая толщину облицовки, штукатурки) в уровне нижнего этажа выше цоколя на всю высоту здания, которая измеряется от уровня пола с нижнего этажа до самого верха утеплителя на чердачном перекрытии.

Чтобы определить объем наземной части дома без чердачного перекрытия, умножьте площадь поперечного вертикального сечения на длину здания, которую измеряйте между наружными поверхностями противоположных торцовых стен по направлению, перпендикулярному площади сечения на уровне нижнего этажа выше цоколя. Эту площадь сечения рассчитывайте обводом по наружной поверхности стен, и учитывая верхние очертания кровли и уровень чистого пола с нижнего этажа.

Если в здании есть выступающие детали и ниши, то при измерении поперечного сечения они не учитываются. Если этажи имеют разную площадь, тогда объем здания определяйте как сумму объемов его частей. Кроме того, отдельно рассчитывайте объемы отдельных частей здания, если они значительно отличаются по своей форме. В таких случаях разграничивающую стену учитывайте в ту часть, которой она соответствует по конструкции или высоте.

Строительный объем здания с подвалом определяйте как сумму объемов подвальной и наземной частей.

Учтите, что объем веранды, эркера и других частей, которые увеличивают его полезный объем, необходимо рассчитывать отдельно и включать в общий объем. Не включайте только в объем здания объемы портиков и открытых балконов.

Видео по теме

Источники:

• строительный объем это

Оценка объема помещений довольно часто требуется при производстве строительных и ремонтных работ. В большинстве случаев это требуется для уточнения количества материалов, необходимых для проведения ремонта, а также для подбора эффективной системы отопления или кондиционирования воздуха. Количественные характеристики, описывающие пространство, как правило, требуют проведения некоторых измерений и несложных вычислений.

Инструкция

Самый простой случай – когда требуется определить объем помещения правильной прямоугольной или квадратной формы. При помощи рулетки измерьте в метрах длину и ширину стен, а также высоту помещения. Удобнее всего проводить измерения по полу, вдоль плинтусов. Перемножьте полученные показатели и вы получите искомый объем.

Если помещение имеет неправильную или сложную форму, задача немного усложняется. Разбейте площадь помещения на несколько простых фигур (прямоугольников, квадратов, полуокружностей и так далее) и вычислите площадь каждой из них, предварительно произведя замеры. Сложите полученные значения, суммируя площадь. Умножьте сумму на высоту помещения. Измерения необходимо проводить в одних и тех же единицах, например, в метрах. При проведении строительных работ определение объема всего сооружения определяется по стандартам. Так называемый строительный объем наземной части здания с чердаком можно вычислить, умножив площадь горизонтального сечения по внешним обводам на уровне нижнего этажа. Измерьте полную высоту здания от уровня чистого пола до верхней части утеплителя чердачного перекрытия. Перемножьте оба показателя.

При наличии разных по площади этажей общий объем помещений в здании определите, сложив объемы всех частей. Таким же образом определяется объем, если помещения имеют разные очертания и конструкцию.

Отдельно вычислите объемы веранд, эркеров, тамбуров и иных вспомогательных элементов сооружения (за исключением крытых и открытых балконов). Включите эти данные в общий объем всех помещений здания.

Чтобы узнать стоимость строения, необходимо определить объем здания. Все данные, полученные в результате измерений, записываются в ведомость по объемам работ, которая является самым важным документом при определении сметной стоимости объекта.

Инструкция

Если строится здание с чердачным перекрытием, то для измерения наземной части умножьте площадь горизонтального сечения (по внешнему обводу здания выше цокольного этажа) на высоту здания (от уровня «чистого» пола на первом этаже, до самой верхней части чердачного перекрытия).

При отсутствии перекрытия умножьте площадь вертикального поперечного сечения на длину, которую нужно измерять в направлении перпендикулярном площади сечения. Все измерения проводите на уровне выше цоколя.

Включите объем световых фонарей, которые будут выступать за очертание крыши. Учтите объем веранды, эркера и тамбура, а также тех частей, которые могут увеличить показатель. Лоджию не вычитайте из общей суммы, но не учитывайте проезды, портики и балконы.

Вычислите объем технических этажей и мансарды, которые определяются умножением горизонтального сечения на высоту от чистого пола и до верха перекрытия мансарды. Если поверхность неровная и имеются изгибы в конструкции, что в результате затрудняет измерения, учтите средний показатель.

Определите объем подвала или полуподвала и прибавьте его к остальным значениям. Если у этажей разная площадь, то нужно определять объем как сумму всех его частей. Отдельно измеряются те места, которые другое очертание или конструкцию.

Измерения по внешнему обводу проводите с учетом толщины штукатурки и облицовки. Строительный объем определяется как сумма всех подвалов, мансард, лоджий, помещений, которые входят в надземную часть здания.

Видео по теме

Полезный совет

Составляя ведомости об объемах работ, пользуйтесь только технической и нормативной документацией. Не придумывайте собственных методов измерения, а пользуйтесь уже проверенными схемами, которые наглядно дают представление о проведении подсчетов и об их последовательности. Определение объема осуществляется по определенным правилам, иначе документ впоследствии не будет учтен.

www.kakprosto.ru

Как найти объём квадрата

Очень часто школьники делают запросы в поисковой системе: как найти объем квадрата. Ответ может быть только один: это невозможно. Квадрат — двумерная фигура (два параметра: длина и ширина). Для вычисления объема необходимо наличие третьей характеристики: высоты. Возможно, имеется ввиду вычисление площади квадрата, его периметра или вычисление объема и площади поверхности куба.

Инструкция

• Квадрат — равносторонний четырехугольник, в котором каждый угол равен 90°. Чтобы найти площадь (S) нужно умножить его длину (l) на ширину (b). Так как в этой фигуре длина и ширина равны, то достаточно знать одну из величин. Единицы измерения площади: см?, м?, км? и т.д.Например: длина одной стороны квадрата = 5 см. Нужно вычислить площадь. Найдите ее по формуле: S = l * b.
  S = 5см * 5см.
  S = 25см?.
  Ответ: площадь квадрата со стороной 5 см равна 25 см?.
• Куб — многогранник, в котором каждая грань – квадрат. Куб имеет двенадцать ребер, которые равны друг другу (т.е длина, ширина и высота одной грани – это длина (высота) ребра) и шесть одинаковых сторон. Чтобы найти объем куба, необходимо перемножить три его ребра (а). Единицы измерения объема: см?, дм?, м? и т.п.Например: длина ребра 5 см. Нужно найти объем куба. Рассчитайте по формуле:
  V = а * а * а или V = a?.
  V = 5см * 5см * 5 см.
  V = 125 см?
  Ответ: объем куба с длиной ребра 5 см равен 125 см?.
• Если необходимо вычислить площадь всех сторон куба, то сначала найдите площадь одной стороны, а потом суммируйте площади всех шести сторон. Например: известно, что длина одной грани куба 5 см. Нужно найти площадь его поверхности. Решение имеет вид :
  1. S = 5см*5 см = 25см?
  2. ? = S+ S+ S+ S+ S+ S или S? =6*S
  S?= 6*25см? = 150см?
  Ответ: площадь поверхности куба с длиной ребра 5 см — 150см?Если требуется найти одну из геометрических характеристик, зная объем куба или площадь квадрата, то из значения объема извлекается кубический корень, а из значения площади — квадратный.
• Периметр квадрата представляет собой сумму длин всех сторон. Т.е. нужно сложить значения четырех его длин.Например: длина квадрата 5 см. Вычислите периметр. Для вычисления периметра любого прямоугольника можно воспользоваться формулой: P = 2*(l+b).
  Для квадрата формула имеет упрощенный вид: P = 4*l
  P = 4*5см = 20см
  Ответ: периметр квадрата длиной 5см – 20см.

completerepair.ru

Как посчитать площадь стен комнаты (калькулятор онлайн)

Калькулятор расчёта плитки на пол
Если вы хотите посчитать только площадь комнаты, то вам сюда.

А для автоматического расчёта площади стен вы можете воспользоваться калькулятором, который расположен ниже по тексту. Для расчёта необходимо измерить в метрах длину, ширину комнаты и высоту потолка.

Дробные значения вводите с запятой!

Чуть ниже приведён практический пример расчета площади стен комнаты.

Обращаем ваше внимание, что измерения необходимо проводить в метрах. Т.е. если вы получили длину комнаты 425 сантиметров, то в поля необходимо ввести значение 4,25. Обратите внимание, что дробные числа нужно вводить с запятой, а не с точкой! Т.е. 5,2 — правильно,   5.2 — неправильно!

О том, как рассчитать обои для комнаты мы уже писали в статье Сколько надо обоев , и конечно же Расчет обоев на комнату.

А сейчас пример расчёта площади стен комнаты. Длина нашей комнаты 3,82 метра, ширина — 3,44 метра и высота потолка 2,71 метра. Подставив эти значения в соответствующие поля мы получим значение 39,349199999999996 квадратных метра, таким образом площадь наших стен будет почти 40 метров.

Значение полученное при расчёте будет не корректно, так как в рассчитанное значение будет входить площадь окна и площадь двери. Эти площади нужно вычесть из полученного значения.

Рекомендуем использовать следующие калькуляторы:

Расчет обоев на комнату

Как посчитать площадь окна

Расчёт плитки для пола

domolov.ru

как рассчитать количество? Калькуляторы, советы

Краткое содержание статьи:

Столкнуться с необходимостью определить, сколько квадратных метров в кубе можно не только на уроках математики, но и в жизни. Чаще всего такие расчеты производятся при строительстве. Для того, чтобы не допустить ошибок в расчете объема и стоимости стройматериала, нужно знать и уметь определить эти величины самостоятельно.

Для чего измерять кубометры?

Необходимость вычислить кубометры может возникнут в первую очередь при ремонтно-строительных работах. Кубический метр – это мера объема, которой измеряется множество строительных материалов, таких как:

1. Лес;
2. Кирпич;
3. Газоблок;
4. Бетон.

Квадратные метры – мера площади. Разница между этими двумя показателями в том, что для вычисления первой надо знать три величины исследуемого объекта:

• Высоту;
• Ширину;
• Длину.

А для вычисления площади достаточно всего двух:

1. Длины;
2. Ширины.

Таким образом понятно, что для вычисления кубометра нужна площадь изделия. Надо отметить, что все расчеты в данном случае производятся исключительно в метрах. То есть все величины, которые измерены в сантиметрах до начала расчетов необходимо перевести в метры.

Если есть такие данные, как длина, ширина и высота, можно посчитать с помощью этого или этого онлайн-калькулятора.

Сколько в кубическом метре квадратных метров?

При расчете кубометра имейте в виду, что стандартом является куб, каждая грань которого равна одному квадратному метру. Таким образом, высота, длина и ширина такого куба одинакова.

Для того чтобы измерить кубометр квадратными метрами необходимо:

• Измерить высоту требуемого предмета;
• Перевести ее в метры;
• Разделить один квадрат на получившее значение высоты.

Таким образом, измерить кубометр материала совсем не сложно. Для этого нужно знать всего три метрические единицы. Принимая во внимание, что в данном случае две из них равны одному, то нам остается всего лишь разделить единицу на высоту изделия.

Как измерить количество предметов в кубе?

Если вам нужно рассчитать объем материала в штуках, помещающихся в куб, можно сделать следующие расчеты:

1. Рассчитать площадь одного предмета, то есть умножить длину на ширину;
2. Перевести получившееся значение в квадратные метры;
3. После один квадрат разделить на площадь одного предмета. Так вы получите число предметов, входящих в один квадратный метр;
4. Измерить высоту объекта;
5. Перевести ее в метры;
6. Разделить один квадрат высоты на высоту объекта. Таким образом вы узнаете число квадратных метров материала в кубе;
7. Умножить число предметов на количество квадратных метров.

Таким образом вы получите объем строительных материалов в штуках. Такие расчеты используются для выяснения числа кирпичей или газоблоков.

Также, таким образом при необходимости можно посчитать требуемое количество любого стройматериала, у которого есть длина, ширина и высота. Например, ламината или напольной плитки.

Определение количества досок в одном кубометре леса

Для строительства лес, как правило, продают в строительных магазинах кубами. Свои подсчеты хозяева обычно ведут в штуках. Для того, чтобы понимать:

1. Сколько кубов леса заказывать;
2. Или наоборот, сколько досок получится в одном кубе, надо предварительно сделать некоторые расчеты.

Перед тем, как начинать их, уточните у продавца длину одной доски. Разные поставщики предлагают разный лес. У кого-то это шестиметровый брус, у кого-то трехметровый, а у кого-то могут быть и 1 метр 20 сантиметров. А также узнайте стандартную высоту и ширину. Обычно она около 2 – 2,5 сантиметров.

Зная исходную длину, считаем сколько таких досок в кубическом метре:

• Умножаем длину бруса на необходимую вам и согласованную заранее с магазином ширину. При этом помним, что расчеты производятся в метрах. Так мы узнаем площадь одной доски;
• Делим один квадрат на площадь одного бруса. Получаем количество досок в одном квадрате;
• Делим один квадрат на высоту бруска, переведенную в метры. В нашем случае 2,5 см = 0,025 м. Получаем число квадратов в кубе;
• Умножаем количество досок в одном квадрате на число квадратных метров в кубе.

Таким образом, определив количество необходимых досок в кубе вы сможете заказать нужное вам число кубометров для строительства.

Количество бетона в кубометрах

В бетонных работах также используются величины квадратного и кубического метража. Секрет заключается в том, что перед вызовом специальной машины с бетоном:

1. Вам потребуется измерить площадь участка, который вы планируете бетонировать;
2. Определиться с глубиной заливки;
3. Перевести все величины в метры;
4. Перемножить их между собой.

Так вы получите количество бетона, которое необходимо залить на ваш участок, для получения желаемой высоты бетонной подушки. Однако, при заказе раствора не следует указывать точную цифру. Лучше заказать немного больше, так как могут быть погрешности в ровности сторон участка и глубины заливки.

Таким образом, для того, чтобы узнать сколько квадратных метров в кубе, надо всего лишь знать высоту предмета, который вам необходимо измерить. Путем простого деления одного куба на этот показатель, вы уже получите требуемую величину. А в дальнейшем она поможет вам рассчитать более детально количество требуемого материала.

Видео: подсчет количества досок в кубе

В данном ролике математик Михаил Бураков расскажет о простом методе подсчета количества досок в одном кубе материала:

znay.co

Как высчитать квадратный метр

1. Идеи потолков
2. Вопросы и ответы
3. Вооружившись рулеткой, можно приступать

В процессе ремонтных или строительных работ владельцу дома приходится осваивать много навыков. Ему необходимо будет научиться также и тому, как рассчитать квадратуру стен, чтобы купить нужное количество краски или обоев, узнать, как высчитать квадратуру пола в каждой комнате, чтобы приобрести ламинат, и, наконец, как рассчитать площадь помещения в квадратных метрах, чтобы составить смету или оплатить труд рабочих.

Как узнать квадратуру комнаты

На определенном этапе времени перед каждым из нас встает проблема, как посчитать квадратуру. Это необходимо как для оплаты за коммунальные услуги, так и во время ремонта, когда нужно узнать, сколько рулонов обоев необходимо, чтобы полностью обклеить стены, или сколько банок лака или краски придется купить.

Конечно, сколько кв. м в каждой комнате квартиры, можно посмотреть в ее техническом паспорте, в котором представлена четкая планировка всей квартиры, указаны квадратные метры каждого помещения, а также общая площадь всего дома. Однако специалисты говорят, что зачастую в этом документе расчет квадратуры бывает сделан неправильно, и практически всегда площадь, указанная в нем, и фактическая площадь разнятся в несколько кв. м.

Поэтому тем, кто хочет правильно вычислить площадь помещения, придется сделать это самостоятельно. Для этого понадобятся самые примитивные геометрические познания. Итак, как рассчитать квадратные метры помещения. Для этого нужно иметь под рукой:

• карандаш и бумагу;
• метр – рулетку;
• калькулятор.

Зная высоту, ширину и длину комнаты, можно использовать не ручной, а онлайн-калькулятор, который с легкостью можно найти в Интернете. Если высчитывается площадь комнаты в форме квадрата, то используется формула, по которой в школе рассчитывалась площадь квадрата. Например, если размер помещения, в основе которого квадрат — 3х3 (метр), то ее площадь составляет девять кв. м.

В случае, если необходимо высчитать метраж комнаты прямоугольной формы, то используется формула площади прямоугольника: S= a*b, где:

а – длина;

b — ширина.

Как рассчитать квадратные метры стен

Онлайн-калькулятор, который представлен практически на всех специализированных сайтах – это отличная возможность моментально рассчитать кв. метры поверхности стен. Высчитывать эту величину необходимо для того, чтобы правильно определить необходимое количество строительного материала.

Удобный онлайн-калькулятор дает возможность не только подсчитать количество квадратных метров, но и количество, например, обоев, которое необходимо для конкретной квартиры или комнаты.

Вообще, онлайн калькулятор является очень удобным инструментом для тех, кто не знает, как рассчитать кв. метры площади стен, однако, чтобы им воспользоваться, нужно правильно ввести все параметры:

• длину;
• ширину комнаты;
• высоту.

Но если по какой-либо причине калькулятор в Интернет сети недоступен, то расчитать квадратуру комнаты и площадь стен в квадратных метрах придется вручную, по следующей формуле:

S = Р х С, где:

S – площадь стен (в кв.м)

Р – периметр комнаты (в метрах)

С – высота стен (в метрах).

Перед тем, как рассчитать квадратные метры стен, необходимо узнать периметр комнаты. В случае, если помещение – квадрат, то периметр считается легко: просто длина стены умножается на четыре, но в случае прямоугольника следует периметр комнат считается по формуле:

Р = (А + В) х 2, где:

A – длина (метр)

B – ширина (метр).

Но перед тем, как высчитать квадратный метр стен, нужно рассчитать квадраты дверных и оконных проемов, если таковые есть. Это нужно для того, чтобы из общей площади стены в квадратных метрах вычесть площадь окон и дверей, чтобы не покупать лишний стройматериал.

При этом тем, кто интересуется, как рассчитать квадратуру комнаты, следует учесть, что квадраты комнат с выступами или же углублениями будут отличаться от аналогичного параметра комнат, форма которых квадрат или прямоугольник, не на один квадратный метр. Вот почему следует к полученной величине площади таких комнат добавлять каждый квадратный метр углубленного участка или выступа.

Как посчитать квадратуру комнаты

Проще всего осуществлять вычисления квадратной площади комнат, которые в форме представляют собой квадрат. Однако таких комнат в доме бывает очень мало, поэтому калькулятор для математических вычислений все-таки понадобится. Те, кто хорошо знает, как высчитать квадратуру комнаты, знают, что замеры нужно делать у прямоугольной поверхности — потолка, пола, стены.

Для начала нужно взять метр и измерить длину и ширину данной поверхности. Помещения квартиры очень редко бывают идеально правильными. Поэтому чтобы узнать относительно точную квадратную площадь, следует провести не один, а несколько замеров. К примеру, общеизвестно, что ровные стены – большая редкость, поэтому лучше всего измерять полы комнат сначала в одном их конце, затем – посередине и в самом конце.

После этого путем нахождения средней арифметической, уже можно получить сравнительно четкую картину. Среднюю арифметическую величину посчитать достаточно просто: для этого данные, замеренные с помощью метра в нескольких местах, складываются, и получившаяся сумма делится на количество замеров.

Таким образом, после того, как получены ширина и длина помещения, уже можно узнать, можно узнать метраж (в кв. м). Формула для этого крайне простая: ширина, например, 3 метра, умножается на высоту, к примеру, на 2 метра. Данная формула позволяет точно высчитать метраж комнат с правильной формой.Но если помещение нестандартной формы, если в нем есть ниши, колонны, выступы и т. п., это его сначала необходимо разбить на удобные для измерений формы – на квадрат или прямоугольник.

К примеру, ниши измеряют отдельно, выступы тоже, то же самое касается колонн и прочих имеющихся элементов интерьера, которые также измеряют отдельно. Предположим, в помещении создано две ниши. Чтобы узнать площадь пола в квадратных метрах, нужно замерить длину и ширину самого помещения, затем первой ниши, а затем второй ниши. Обе длины ниш складываются и записываются на бумаге. Затем складывается ширина этих ниш. Чтобы узнать количество квадратных метров, полученные две цифры перемножаются и добавляются к общим квадратным метрам основного помещения.

В случае нестандартной планировки пространство комнат разбивается на удобные составляющие. Это могут быть как квадрат и прямоугольник, так и треугольник и даже круг. И чтобы посчитать кв. м каждой из этих фигур, нужно воспользоваться соответствующей формулой.

К примеру, прямоугольник и квадрат считаются умножением длины на ширину. Для круга используется формула расчета площади круга, а для треугольника — формула расчета площади треугольника. Все эти формулы есть в любом математическом справочнике, а можно в Интернете найти онлайн калькулятор. Затем все полученные данные складываются.

Перед тем, как рассчитать квадратные метры пола или потолка помещения неправильной формы, следует по возможности точно начертить на бумаге план, а затем разбить его на простые фигуры, измерить их площади и прибавить друг к другу. Для такого способа исчисления понадобятся только метр или рулетка и калькулятор.

Измерять площадь окружности нужно по формуле πr2, где r – радиус окружности или длина отрезка от центра до любой точки на окружности. Измерив это расстояние, а затем, умножив его на постоянную величину π на калькуляторе, получаем площадь круга. Если под рукой нет калькулятора, на котором есть функция числа π, то нужно использовать цифру 3.14. Причем производить замеры круга нужно как минимум вдвоем: один человек стоит с рулеткой, а другой водит другим концом с по окружности.

Вычисление квадратуры более сложных изогнутых поверхностей потребует немного более углубленных знаний математики. Тем, кто проводит замеры с практическими целями, будет намного легче, если они попробуют представить изогнутую поверхность в виде нескольких прямых линий.

Это нужно знать

Для измерений нужно использовать одну и ту же рулетку. Замеры нужно делать, расположив ее под прямым углом, то есть две линии комнаты, будь то квадрат или прямоугольник, на месте стыка измеряются под прямым углом по отношению друг к другу.

Если измеряемая длина получилась немного меньше метра, то, делая замеры, нужно округлять в сторону ближайшего сантиметра. К примеру, если ширина составляет немного больше отметки одного метра восьми сантиметров, то следует так и посчитать, игнорируя миллиметры.

Обычно полученные ширина или длина комнат не составляют ровную цифру: показатели получаются в метрах и в сантиметрах, к примеру, «3 метра 25 сантиметров». В этом случае за единицу измерения можно взять как метр, так и сантиметр, получив 3,25 метра или 325 сантиметров.

Умножив ширину на длину, получается вычислить площадь в квадрат. метрах. Но перед этим данные нужно перевести в одну единицу измерения. При необходимости можно использовать калькулятор. Например, 3,25м х 4,55м = 14,7875 квадратных метра (м2). Округлять нужно в большую сторону: 14,7875 округляются до 14,8 м2.

Проявлять скрупулезность и считать миллиметры не стоит. Вряд ли вручную стены и пол можно измерить с точностью до одного мм, поэтому округлять нужно до ближайшего см. Но если нужны максимально точные данные, например, если замеры проводятся перед тем, как сделать натяжной потолок, значащую цифру нужно увеличить.

Многим из тех, кто планирует пользоваться услугами какой-либо строительной фирмы, лучше перед началом работ обязательно вызвать специалиста, который, замерив геометрический периметр, определив фигуру комнаты, число простых и сложных форм — ниш и выступов, ниш, а также определив значения прочих величин, представит предварительную смету.

Если предстоит сделать и внешнюю отделку, то нужно будет измерить также крышу и всю конструкцию. Осуществив замеры и переведя показатели в единую систему единиц, специалист сможет не только правильные размеры, но и итоговый результат, по которому будут рассчитываться предстоящие расходы как на проведение всех строительных работ, так и необходимый объем строительных материалов.

ceilingideas.ru

Калькулятор для расчета объема параллелепипеда

C помощью нашего Онлайн-калькулятора для расчета объема параллелепипеда Вы можете быстро и точно рассчитать объем прямоугольного параллелепипеда. Для того, чтобы вычислить объем прямоугольного параллелепипеда, введите значение ребер “a”, “b”, “c” и нажмите кнопку “Рассчитать”. Также Вы можете указать точность полученного результата, т.е. количество знаков после запятой, до которого будет округлен рассчитанный объем параллелепипеда.

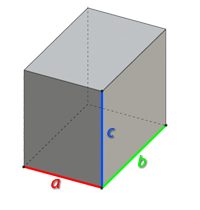
Задайте значение ребер параллелепипеда а, b, c и нажмите кнопку “Рассчитать”

Округлить результат до

знаков после запятой

Рассчитать

Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.

Объем прямоугольного параллелепипеда вычисляется по следующей формуле:
,
где a, b, c – ребра параллелепипеда.

Введите а — сторону квадрата в мм (миллиметрах):

Введите h — толщину квадрата в мм (миллиметрах):

Как рассчитать объем квадрата?

Если квадрата имеет толщину, то фактически это параллелепипед. Объем параллелепипеда в основании которого лежит квадрат  в общем случае рассчитывается по формуле:

V = a x a х h

V — объем параллелепипеда. Объем квадрата имеющего толщину (высоту).

a — сторона квадрата основания параллелепипеда

h — толщина квадрата (высота квадрата)

Объем в миллиметрах кубических квадрата имеющего толщину (параллелепипед):

V_мм3 = a_мм х a_мм х h_мм

V_мм3 — объем в миллиметрах кубических (мм³).

a_мм — сторона квадрата в миллиметрах (мм).

h_мм — толщина квадрата в миллиметрах (мм).

Объем в сантиметрах кубических квадрата имеющего толщину (параллелепипед):

V_см3 = a_мм х a_мм х h_мм / 1 000

V_см3 — объем в сантиметрах кубических (см³).

a_мм — сторона квадрата в миллиметрах (мм).

h_мм — толщина квадрата в миллиметрах (мм).

Объем в метрах кубических квадрата имеющего толщину (параллелепипед):

V_м3 = a_мм х a_мм х h_мм / 1 000 000 000

V_м3 — объем в метрах кубических (м³).

a_мм — сторона квадрата в миллиметрах (мм).

h_мм — толщина квадрата в миллиметрах (мм).

Объем в литрах квадрата имеющего толщину (параллелепипед):

V_л = a_мм х a_мм х h_мм / 1 000 000

V_л — объем в литрах (л).

a_мм — сторона квадрата в миллиметрах (мм).

h_мм — толщина квадрата в миллиметрах (мм).

Формулы объема геометрических фигур

Объем куба

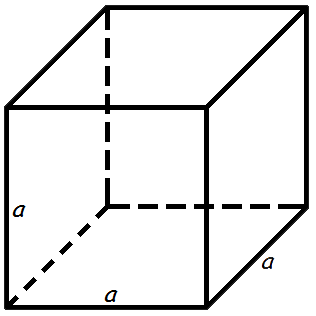
Объем куба равен кубу длины его грани.

Формула объема куба:

Объем призмы

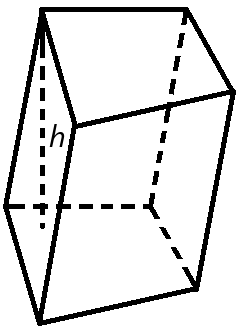
Объем призмы равен произведению площади основания призмы, на высоту.

Формула объема призмы:

Объем параллелепипеда

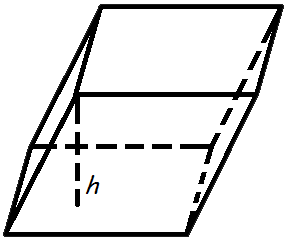
Объем параллелепипеда равен произведению площади основания на высоту.

Формула объема параллелепипеда:

Объем прямоугольного параллелепипеда

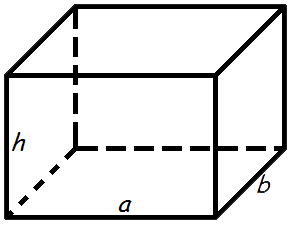
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.

Формула объема прямоугольного параллелепипеда:

Объем пирамиды

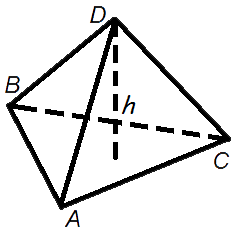
Объем пирамиды равен трети от произведения площади ее основания на высоту.

Формула объема пирамиды:

Объем правильного тетраэдра

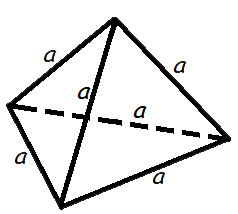
Формула объема правильного тетраэдра:

Объем цилиндра

Объем цилиндра равен произведению площади его основания на высоту.

Формулы объема цилиндра:

Объем конуса

Объем конуса равен трети от произведению площади его основания на высоту.

Формулы объема конуса:

Объем шара

Объем шара равен четырем третьим от его радиуса в кубе помноженного на число пи.

Формула объема шара:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Все формулы объемов геометрических тел

1. Расчет объема куба

a – сторона куба

Формула объема куба, (V):

2. Найти по формуле, объем прямоугольного параллелепипеда

a , b , c – стороны параллелепипеда

Еще иногда сторону параллелепипеда, называют ребром.

Формула объема параллелепипеда, (V):

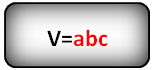
3. Формула для вычисления объема шара, сферы

R – радиус шара

По формуле, если дан радиус, можно найти объема шара, (V):

4. Как вычислить объем цилиндра ?

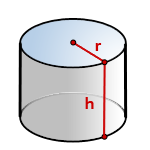
h – высота цилиндра

r – радиус основания

По формуле найти объема цилиндра, есди известны – его радиус основания и высота, (V):

5. Как найти объем конуса ?

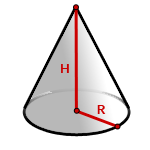
R – радиус основания

H – высота конуса

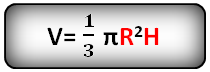
Формула объема конуса, если известны радиус и высота (V):

7. Формула объема усеченного конуса

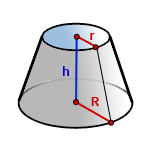
r – радиус верхнего основания

R – радиус нижнего основания

h – высота конуса

Формула объема усеченного конуса, если известны – радиус нижнего основания, радиус верхнего основания и высота конуса (V ):

8. Объем правильного тетраэдра

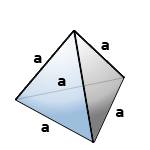
Правильный тетраэдр – пирамида у которой все грани, равносторонние треугольники.

а – ребро тетраэдра

Формула, для расчета объема правильного тетраэдра (V):

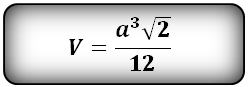
9. Объем правильной четырехугольной пирамиды

Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.

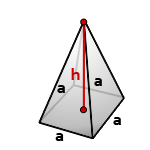
a – сторона основания

h – высота пирамиды

Формула для вычисления объема правильной четырехугольной пирамиды, (V):

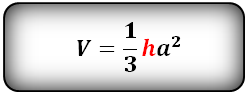
10. Объем правильной треугольной пирамиды

Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.

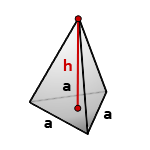
a – сторона основания

h – высота пирамиды

Формула объема правильной треугольной пирамиды, если даны – высота и сторона основания (V):

11. Найти объем правильной пирамиды

Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.

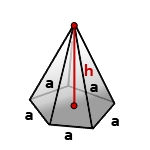
h – высота пирамиды

a – сторона основания пирамиды

n – количество сторон многоугольника в основании

Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):

Формула объема.

Формула объема необходима для вычисления параметров и характеристик геометрической фигуры.

Объем фигуры – это количественная характеристика пространства, занимаемого телом или веществом. В простейших случаях объём измеряется числом умещающихся в теле единичных кубов, т. е. кубов с ребром, равным единице длины. Объём тела или вместимость сосуда определяется его формой и линейными размерами.

Параллелепипед.

Объем прямоугольного параллелепипеда равен произведению площади основания на высоту.

Цилиндр.

Объем цилиндра равен произведению площади основания на высоту.

Объем цилиндра равен произведению числа пи (3.1415) на квадрат радиуса основания на высоту.

Пирамида.

Объем пирамиды равен одной трети произведения площади основания S (ABCDE) на высоту h (OS).

Правильная пирамида — это пирамида, в основании, которой лежит правильный многоугольник, а высота проходит через центр вписанной окружности в основание.

Правильная треугольная пирамида — это пирамида, у которой основанием является равносторонний треугольник и грани равные равнобедренные треугольники.

Правильная четырехугольная пирамида — это пирамида, у которой основанием является квадрат и грани равные равнобедренные треугольники.

Тетраэдр — это пирамида, у которой все грани — равносторонние треугольники.

Усеченная пирамида.

Объем усеченной пирамиды равен одной трети произведения высоты h (OS) на сумму площадей верхнего основания S₁(abcde), нижнего основания усеченной пирамиды S₂ (ABCDE) и средней пропорциональной между ними.

Куб.

Вычислить объем куба легко – нужно перемножить длину, ширину и высоту. Так как у куба длина равна ширине и равна высоте, то объем куба равен s 3 .

Конус — это тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.

Усеченный конус получится, если в конусе провести сечение, параллельное основанию.

V = 1/3 πh (R 2 + Rr + r 2 )

Шар.

Объем шара в полтора раза меньше, чем объем описанного вокруг него цилиндра.

Призма.

Объем призмы равен произведению площади основания призмы, на высоту.

Сектор шара.

Объем шарового сектора равен объему пирамиды, основание которой имеет ту же площадь, что и вырезаемая сектором часть шаровой поверхности, а высота равна радиусу шара.

Шаровой слой — это часть шара, заключенная между двумя секущими параллельными плоскостями.

Сегмент шара – это часть шара, осекаемая от него какой-нибудь плоскостью, называется шаровым или сферическим сегментом

[spoiler title=”источники:”]

http://www-formula.ru/2011-09-24-00-37-25

http://www.calc.ru/Formula-Obyema.html

[/spoiler]

Фигура	Формула	Чертеж

Объемы геометрических фигур.