Как найти объем квадратной пирамиды

Загрузить PDF

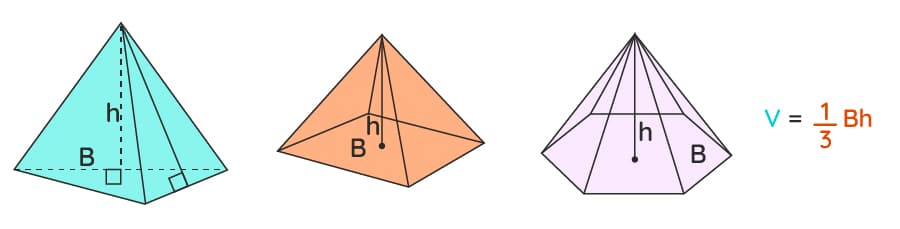
Квадратная пирамида – объемная фигура с основанием в виде квадрата и треугольными боковыми гранями. Вершина квадратной пирамиды проецируется в центр основания. Если «а» – сторона квадратного основания, «h» – высота пирамиды (перпендикуляр, опущенный из вершины пирамиды к центру ее основания), тогда объем квадратной пирамиды можно вычислить по формуле: a² × (1/3)h. Эта формула верна для квадратной пирамиды любых размеров (от сувенирных пирамид до египетских пирамид).

1
Найдите сторону основания. Так как в основании квадратной пирамиды лежит квадрат, то все стороны основания равны. Поэтому необходимо найти длину любой стороны основания.
- Например, дана пирамида, сторона основания которой равна 5 см.
- Если стороны основания не равны друг другу, то вам дана прямоугольная, а не квадратная пирамида. Тем не менее, формула для вычисления объема прямоугольной пирамиды похожа на формулу для вычисления объема квадратной пирамиды. Если «l» и «w» – две смежные (неравные) стороны прямоугольника в основании пирамиды, то объем пирамиды вычисляется по формуле: (l× w) × (1/3)h
2
Вычислите площадь квадратного основания, умножив его сторону саму на себя (или, другими словами, возведя сторону в квадрат).
- В нашем примере: 5 х 5 = 5² = 25 см².
- Не забудьте, что площадь измеряется в квадратных единицах – квадратных сантиметрах, квадратных метрах, квадратных километрах и так далее.
3
Умножьте площадь основания на высоту пирамиды. Высота – перпендикуляр, опущенный из вершины пирамиды на ее основание. Перемножив эти величины, вы получите объем куба с тем же основанием и высотой, как у пирамиды.
- В нашем примере высота равна 9 см: 25 см² × 9 см = 225 см³
- Не забывайте, что объем измеряется в кубических единицах, в данном случае в кубических сантиметрах.
4
Разделите полученный результат на 3 и вы найдете объем квадратной пирамиды.
- В нашем примере: 225 см³ / 3 = 75 см³.
- Объем измеряется в кубических единицах.
Реклама

1
Если вам дана либо площадь, либо высота пирамиды и ее апофема, вы можете найти объем пирамиды, используя теорему Пифагора. Апофема – это высота наклонной треугольной грани пирамиды, проведенная из вершины треугольника к его основанию. Для вычисления апофемы используйте сторону основания пирамиды и ее высоту.
- Апофема делит сторону основания пополам и пересекает ее под прямым углом.
2
Рассмотрите прямоугольный треугольник, образованный апофемой, высотой и отрезком, соединяющим центр основания и середину его стороны. В таком треугольнике апофема является гипотенузой, которую можно найти по теореме Пифагора. Отрезок, соединяющий центр основания и середину его стороны, равен половине стороны основания (этот отрезок является одним из катетов; вторым катетом является высота пирамиды).
- Напомним, что теорема Пифагора записывается так: a² + b² = c², где «a» и «b» – катеты, «c» – гипотенуза прямоугольного треугольника.
- Например, дана пирамида, у которой сторона основания равна 4 см, а апофема – 6 см. Чтобы найти высоту пирамиды, подставьте эти значения в теорему Пифагора.
  - a² + b² = c²
  - a² + (4/2)² = 6²
  - a² = 32
  - a = √32 = 5,66 см Вы нашли второй катет прямоугольного треугольника, который является высотой пирамиды (аналогично, если была бы дана апофема и высота пирамиды, вы бы могли найти половину стороны основания пирамиды).
3
Используйте найденное значение, чтобы найти объем пирамиды по формуле: a² × (1/3)h.
- В нашем примере вы вычислили, что высота пирамиды равна 5,66 см. Подставьте необходимые значения в формулу для вычисления объема пирамиды:
  - a² × (1/3)h
  - 4² × (1/3)(5,66)
  - 16 × 1,89 = 30,24 см³.
4
Если вам не дана апофема, используйте ребро пирамиды. Ребро – это отрезок, соединяющий вершину пирамиды с вершиной квадрата в основании пирамиды. В этом случае вы получите прямоугольный треугольник, катетами которого являются высота пирамиды и половина диагонали квадрата в основании пирамиды, а гипотенузой – ребро пирамиды. Так как диагональ квадрата равна √2 × сторону квадрата, то вы можете найти сторону квадрата (основания), разделив диагональ на √2. Затем вы сможете найти объем пирамиды по вышеописанной формуле.
- Например, дана квадратная пирамида с высотой 5 см и ребром 11 см. Вычислите половину диагонали следующим образом:
  - 5² + b² = 11²
  - b² = 96
  - b = 9,80 см.
  - Вы нашли половину диагонали, поэтому диагональ равна: 9,80 см × 2 = 19,60 см.
  - Сторона квадрата (основания) равна √2 × диагональ, поэтому 19,60 / √2 = 13,90 см. Теперь найдите объем пирамиды по формуле:a² × (1/3)h
  - 13,90² × (1/3)(5)
  - 193,23 × 5/3 = 322,05 см³
Реклама

Советы

В квадратной пирамиде ее высота, апофема и сторона основания связаны теоремой Пифагора: (сторона ÷ 2)² + (высота)² = (апофема)²
В любой правильной пирамиде апофема, сторона основания и ребро связаны теоремой Пифагора: (сторона ÷ 2)² + (апофема)² = (ребро)²

Об этой статье

Эту страницу просматривали 11 790 раз.

Была ли эта статья полезной?

Источник

Download Article

A square pyramid is a three-dimensional solid characterized by a square base and sloping triangular sides that meet at a single point above the base. If represents the length of one of the square base’s sides and represents the height of the pyramid (the perpendicular distance from the base to the point), the volume of a square pyramid can be calculated with the formula $V={frac {1}{3}}s^{2}h$ . It doesn’t matter whether the pyramid is the size of a paperweight or larger than the Great Pyramid of Giza – this formula works for any square pyramid. The volume can also be calculated using what is called the “slant height” of the pyramid.

1

Measure the side length of the base. Since, by definition, square pyramids have bases that are perfectly square, all of the sides of the base should be equal in length. Thus, for a square pyramid, you only need to find the length of one side.^[1]
2
Calculate the area of the base. Finding the volume begins by finding the two-dimensional area of the base. This is done by multiplying the base’s length times its width. Because the base of a square pyramid is a square, its sides all have equal lengths, so the area of the base is equal to the length of one side squared (times itself).^[2]
- In the example, since the side lengths of the pyramid’s base are all 5 cm, you can find the base’s area as:
  - ${text{area}}=s^{2}=(5{text{cm}})^{2}=25{text{cm}}^{2}$
- Remember that two-dimensional areas are expressed in square units – square centimeters, square meters, square miles, and so on.
Advertisement
3
Multiply the area of the base by the pyramid’s height. Next, multiply the base area by the height of the pyramid. As a reminder, the height is the distance of the line segment stretching from the apex of the pyramid to the plane of the base at perpendicular angles to both.^[3]
- In the example, suppose the pyramid has a height of 9 cm. In this case, multiply the area of the base by this value as follows:
  - $25{text{cm}}^{2}*9{text{cm}}=225{text{cm}}^{3}$
- Remember that volumes are expressed in cubic units. In this case, because all the linear measurements are centimeters, the volume is in cubic centimeters.
4
Divide this answer by 3. Finally, find the volume of the pyramid by dividing the value you just found from multiplying the base area by the height by 3. This will give you a final answer that represents the volume of the square pyramid.^[4]
- In the example, divide 225 cm³ by 3 to get an answer of 75 cm³ for the volume.

1

Measure the pyramid’s slant height. Sometimes you will not be told the perpendicular height of the pyramid. Instead, you may be told – or may have to measure – the pyramid’s slant height. With the slant height, you will be able to use the Pythagorean Theorem to calculate the perpendicular height.^[5]
2

Imagine a right triangle. To use the Pythagorean Theorem, you need a right triangle. Imagine a right triangle slicing through the middle of the pyramid and perpendicular to the base of the pyramid. The slant height of the pyramid, called , is the hypotenuse of this right triangle. The base of this right triangle is one half the length of , the side of the square base of the pyramid.^[6]
3
4
5

Use the height and base to calculate volume. After using the calculations with the Pythagorean Theorem, you now have the information you need to calculate the volume of the pyramid as you normally would. Use the formula $V={frac {1}{3}}s^{2}h$ and solve, making sure to label your answer in cubic units.^[9]

1
Measure the pyramid’s edge height. The edge height is the length of the edge of the pyramid, measured from the apex to one of the corners of the pyramid’s base. As before, you will then use the Pythagorean Theorem to calculate the perpendicular height of the pyramid.^[10]
- For this example, assume that the edge height can be measured to be 11 cm and you are given that the perpendicular height is 5 cm.
2

Imagine a right triangle. As before, you need a right triangle to use the Pythagorean Theorem. In this case, however, your unknown value is the base of the pyramid. You know the perpendicular height and the edge height. If you imagine cutting the pyramid diagonally from one corner to the opposite corner and opening it up, the exposed inside face is a triangle. The height of that triangle is the perpendicular height of the pyramid. It divides the exposed triangle into two symmetrical right triangles. The hypotenuse of either right triangle is the edge height of the pyramid. The base of either right triangle is one-half the diagonal of the base of the pyramid.
3
4

Calculate the diagonal of the square base. You will need to rearrange the equation to isolate the variable and then solve for its value.^[11]
5
Find the side of the base from the diagonal. The base of the pyramid is a square. The diagonal of any square is equal to the length of a side times the square root of 2. Conversely, you can find the side of the square from its diagonal by dividing by the square root of 2.^[12]
- For this sample pyramid, the diagonal has been calculated to be 19.6 cm. Therefore, the side is equal to:
  - $s={frac {19.6}{{sqrt {2}}}}={frac {19.6}{1.41}}=13.90$
6

Add New Question

Question

If I have only the volume, how do I solve for height?

You cannot solve for height if all you know is the volume.
Question

In method 1, why did you divide 225 by 3?

Because that’s the formula for the volume: one-third of the product of the base area and the height.
Question

How do I find length?

To find the length of one side of the square base, you must know the height and the volume of the pyramid. To get the length, multiply the volume by three, divide that by the height, and then take that number and find its square root.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Video

In a square pyramid, the perpendicular height, slant height, and length of the edge of the base face are all related by the Pythagorean theorem.

Thanks for submitting a tip for review!

References

About This Article

Article SummaryX

To calculate the volume of a square pyramid, first find the length of one of the sides of the base of the pyramid. Then, calculate the area of the base by squaring the length of the side, and multiply the area by the pyramid’s height. Finally, divide the answer by 3 to find the volume of the square pyramid, and write your answer in units cubed. For tips on finding the volume using slant height or height edge, scroll down!

Did this summary help you?

Thanks to all authors for creating a page that has been read 377,701 times.

Did this article help you?

Источник

Автор:
John Pratt

Дата создания:
15 Январь 2021

Дата обновления:
23 Май 2023

Видео: 11 класс. Геометрия. Объём пирамиды. 28.04.2020.

Содержание

меры
подсказки

Квадратная пирамида представляет собой трехмерное твердое тело, характеризующееся квадратным основанием и наклонными треугольными сторонами, которые встречаются в определенной точке над основанием. Если он представляет длину одной стороны основания и представляет собой высоту пирамиды (расстояние, перпендикулярное основанию до точки), объем квадратной пирамиды можно рассчитать по формуле. Неважно, размером ли это с пресс-папье или больше, чем Великая пирамида в Гизе, формула работает для любой квадратной пирамиды. Объем также можно рассчитать, используя так называемую «наклонную высоту» пирамиды.

меры

Метод 1 из 3: определение объема с учетом площади основания и высоты

Измерьте длину стороны основания. Поскольку по определению пирамиды этого типа имеют идеально квадратные основания, все стороны должны быть равны по длине. Итак, в случае квадратной пирамиды просто определите длину одной стороны.
- Представьте себе пирамиду, основание которой представляет собой квадрат с длинными сторонами. Это значение, которое будет использоваться для определения базовой площади.
- Если стороны основания не равны по длине, у вас будет прямоугольная пирамида вместо квадратной пирамиды. Формула объема в этом случае очень похожа на использованную в другом. Если он представляет длину основания пирамиды и представляет собой ширину, общий объем будет выражен как.
Рассчитайте базовую площадь. Определение объема начинается с шага вычисления двумерной площади основания. Делается это путем умножения длины основания на его ширину. Поскольку основание пирамиды этого типа квадратное, его стороны будут равной длины и, следовательно, площадь основания эквивалентна длине стороны, возведенной в квадрат (умноженной на саму себя).
- В этом примере, поскольку стороны основания пирамиды измеряются, вы можете определить площадь основания как:
- Помните, что двумерные площади выражаются в квадратных единицах – квадратных сантиметрах, квадратных метрах, квадратных милях и т. Д.
Умножьте площадь основания на высоту пирамиды. Затем умножьте площадь основания на высоту пирамиды. Стоит помнить, что высота эквивалентна расстоянию отрезка линии, идущего от вершины пирамиды до основания под углами, перпендикулярными обоим.
- Предположим в этом примере, что пирамида имеет высоту, эквивалентную. В этом случае умножьте базовую площадь на это значение следующим образом:
- Помните, что объемы выражаются в кубических единицах. В этом случае, поскольку линейные размеры указаны в сантиметрах, объем указывается в кубических сантиметрах.
Разделите ответ на. Наконец, определите объем пирамиды, разделив его на значение, полученное при умножении площади основания на высоту. Это приведет к окончательному ответу, который представляет объем квадратной пирамиды.
- В этом примере разделите на, чтобы получить ответ для объема, равного.

Метод 2 из 3: определение объема по наклонной высоте

Измерьте наклонную высоту пирамиды. Иногда вы не знаете, какой высоты пирамида перпендикулярна. Вместо этого вы можете знать или должны измерить свой наклонный рост. С этим значением вы сможете использовать теорему Пифагора при вычислении перпендикулярной высоты.
- Наклонная высота эквивалентна расстоянию от вершины пирамиды до середины одной стороны основания. Следите за тем, чтобы не перепутать середину с одним из углов основания. В этом примере вы могли указать высоту наклона пирамиды, эквивалентную, с длиной стороны.
- Напоминаем, что теорема Пифагора может быть выражена уравнением, где и – перпендикулярные стороны прямоугольного треугольника, а – гипотенуза.
Представьте себе прямоугольный треугольник. Чтобы использовать теорему Пифагора, необходим прямоугольный треугольник. Представьте себе треугольный срез, проходящий через середину пирамиды и перпендикулярный ее основанию. Наклонная высота, называемая, представлена гипотенузой этого прямоугольного треугольника. Его основание, с другой стороны, эквивалентно половине боковой длины квадратного основания.
Установите переменные в значения. Теорема Пифагора использует переменные, и, но полезно заменить эти значения, чтобы они имели реальный смысл в вашей проблеме. В нем наклонная высота занимает место, а катет прямоугольного треугольника, то есть, занимает место. Вы рассчитаете высоту пирамиды, которая займет место.
- Замещение можно выразить следующим образом:
Используйте теорему Пифагора, чтобы вычислить высоту перпендикуляра. Введите измеренные значения и перейдите к решению уравнения:
- (исходное уравнение)
- (квадратный корень с обеих сторон)
- (заменить значения)
- (упростить дробь)
- (упростить квадрат)
- (Вычитание)
- (упростить квадратный корень)
Используйте высоту и базу, чтобы рассчитать объем. После выполнения вычислений по теореме Пифагора у вас теперь будет информация, необходимая для обычного вычисления объема пирамиды. Используйте формулу и решите вопрос, не забывая указывать ответ в кубических единицах.
- В результате расчетов было установлено, что высота пирамиды равна. Используйте это значение со стороной основания, которая эквивалентна, для расчета объема:

Метод 3 из 3. Определите объем, используя высоту границы

Измерьте высоту края пирамиды. Это длина края от вершины до одного из углов основания. Как и раньше, для вычисления перпендикулярной высоты пирамиды необходимо будет использовать теорему Пифагора.
- В этом примере предположим, что высота границы будет указана в, а высота перпендикуляра равна.
Представьте себе прямоугольный треугольник. Как и раньше, для использования теоремы Пифагора необходимо иметь прямоугольный треугольник. Однако в этом случае неизвестное значение представляет собой основание пирамиды. Вы знаете значения перпендикулярной высоты и высоты кромки. Представьте, что вы разрезаете его по диагонали от одного конца до противоположного конца и открываете его: открытая внутренняя часть будет состоять из треугольника. Высота этого треугольника будет перпендикулярной высотой пирамиды, которая делит ее на два симметричных прямоугольных треугольника. Гипотенуза любого из них представляет собой наклонную высоту пирамиды, а основание обоих равно диагональной половине основания пирамиды.
Определите переменные. Используйте этот воображаемый прямоугольный треугольник и определите значения теоремы Пифагора. Вы знаете высоту перпендикуляра ,, которая состоит из одной из ножек, или. Высота ребра пирамиды ,, – это гипотенуза воображаемого прямоугольного треугольника, который занимает место. Неизвестная диагональ основания, в свою очередь, будет оставшимся катетом прямоугольного треугольника, или. После выполнения необходимых замен уравнение будет выражено следующим образом:
Вычислите диагональ квадратного основания. Потребуется переупорядочить уравнение, чтобы изолировать переменную, чтобы найти ее значение.
- (пересмотренное уравнение)
- (заменить с обеих сторон)
- (квадратный корень с обеих сторон)
- (введите числовые значения)
- (упростите высокие значения)
- (вычтите значения)
- (упростить квадратный корень)
- Удвойте это значение, чтобы определить диагональ квадратного основания пирамиды. Следовательно, диагональ будет эквивалентна.
Определите базовую сторону по диагонали. Основание пирамиды – квадрат. Диагональ любого квадрата, в свою очередь, равна длине одной стороны, умноженной на квадратный корень из. И наоборот, вы также можете определить размер стороны квадрата от диагонали, разделив значение на квадратный корень из.
- В этом примере пирамиды было вычислено, что диагональ эквивалентна. Следовательно, сторона будет равна:
Используйте сторону и высоту для расчета объема. Вернитесь к исходной формуле, чтобы рассчитать объем, используя значения для стороны и перпендикулярной высоты.

подсказки

В квадратной пирамиде перпендикулярная высота, наклонная высота и длина основания связаны теоремой Пифагора.

Источник

Объем объекта определяется как трехмерное пространство, которое он занимает, но было бы проще представить его как количество воды, газа или любого другого вещества, которое может удерживать указанный объект. В любом случае, столкнувшись с пирамидой с квадратным основанием – представьте, например, пирамиды Египта – вы можете найти его объем, используя простую формулу, которая требует высоты пирамиды и длины одной стороны вдоль ее база.

TL; DR (слишком длинный; Не читал)

Чтобы найти объем квадратной пирамиды, используйте формулу V = А(час/ 3), где V это объем и А площадь основания.

Соберите, измерьте или вычислите высоту пирамиды и длину одной стороны вдоль ее основания. Рассмотрим пример квадратной пирамиды, у которой одна сторона основания пирамиды составляет 5 дюймов, а высота пирамиды – 6 дюймов.

Оба измерения должны производиться в одних и тех же единицах. Кроме того, чтобы использовать эту формулу, высота должна быть расстоянием от самой верхней вершины пирамиды (ее вершины) до середины основания, нет наклонная высота от вершины пирамиды до одной из ее нижних вершин.

Если вам дана наклонная высота пирамиды, она представляет собой гипотенузу прямоугольного треугольника, образованного им самим, высоту пирамиды и 1/2 длины основания пирамиды. Воспользуйтесь теоремой Пифагора:

а ^ 2 + Ь ^ 2 = с ^ 2

найти высоту пирамиды. В таком случае c наклонная высота пирамиды, а составляет 1/2 длины основания, а б будет высота пирамиды.

Возвести в квадрат длину основания пирамиды или, другими словами, умножить длину на себя. Это дает вам площадь основания пирамиды в квадратных единицах. Чтобы продолжить пример, это будет:

5 text {дюймы} × 5 text {дюймы} = 25 text {дюймы} ^ 2

Умножьте площадь основания пирамиды на высоту пирамиды, затем разделите ответ на 3. Результат – объем вашей пирамиды, записанный в кубах. Чтобы продолжить пример, у вас есть:

25 text {дюймы} ^ 2 × 6 text {дюймы} = 150 text {дюймы} ^ 3

Разделите это на три, чтобы получить объем пирамиды:

150 text {дюймы} ^ 3 ÷ 3 = 50 text {дюймы} ^ 3

Советы

Вы можете использовать ту же процедуру, чтобы найти объем пирамиды с прямоугольным основанием, с одной небольшой модификацией. Вместо того, чтобы находить площадь основания, возводя в квадрат одну сторону от его длины, вы должны найти длину и ширину основания, а затем умножить их вместе, чтобы найти площадь основания. Таким образом, если основание пирамиды имеет размер 5 дюймов на 4 дюйма, площадь ее основания будет 20 дюймов в квадрате.

Источник

Оглавление:

📝 Как это работает?
🤔 Частые вопросы и ответы
📋 Похожие материалы
📢 Поделиться и комментировать

Что считает калькулятор

Калькулятор объема пирамиды — это онлайн инструмент, который используется для быстрого расчета объема пирамиды по ее известным параметрам. Объем пирамиды представляет собой объем пространства, которое занимает эта фигура в трехмерном пространстве.

Калькулятор объема пирамиды может быть полезным инструментом для учебных заданий или практических задач, связанных с расчетами объемов таких геометрических фигур. Он также может использоваться в различных профессиональных областях, где необходимы точные расчеты объемов, например, в архитектуре, инженерии, физике и т.д.

Где можно применить калькулятор объема пирамиды

Калькулятор объема пирамиды можно применить в различных сферах, где требуется вычислить объем пирамиды, например:

Строительство: при проектировании зданий и сооружений инженерам и архитекторам часто нужно вычислить объем пирамиды, например, для расчета объема кровли или фундамента.
Геометрия: в математике пирамиды являются важным объектом изучения, и вычисление их объема – одна из основных задач геометрии.
Производство: в производстве может потребоваться вычислить объем пирамиды для расчета необходимых материалов, например, для производства упаковки.
Учебные цели: калькулятор объема пирамиды может быть использован студентами и учениками при изучении геометрии или математики.
Игры и развлечения: калькулятор объема пирамиды может быть использован в играх и развлечениях, где требуется решить задачу по вычислению объема пирамиды.

В целом, калькулятор объема пирамиды может быть полезен во всех ситуациях, где требуется вычислить объём данной фигуры.

В чем преимущество пирамиды

Пирамида — многогранник, основание которого является многоугольником, а остальные грани – треугольниками, имеющими общую вершину.

Пирамидальная форма имеет несколько преимуществ:

Стабильность. Пирамида имеет широкое основание и суживающийся верх, что делает ее очень стабильной. Это свойство делает пирамиду идеальным выбором для многих инженерных и архитектурных конструкций.
Эффективность использования пространства. Пирамидальная форма позволяет использовать пространство более эффективно. Благодаря своей форме пирамида может поместить больше материала на меньшей площади, чем другие формы.
Видимость. Пирамиды обычно имеют значительную высоту и суживающуюся вершину, что делает их легко заметными издалека. Это свойство делает пирамиды идеальным выбором для монументальных сооружений, таких как пирамиды в Египте или Латинской Америке.
Эстетика. Пирамидальная форма может быть очень эстетичной и привлекательной. Она может использоваться в различных областях, таких как дизайн зданий, декоративное искусство, упаковка продуктов и многое другое.

В целом, пирамидальная форма имеет множество преимуществ, которые делают ее полезной в различных областях. Однако, как и любая другая форма, она может иметь свои недостатки в зависимости от контекста, в котором она используется.

Как вычислить объем пирамиды

Калькулятор объема пирамиды использует стандартные математические формулы для расчета объема пирамиды с основанием любой формы.

Как вычислить объем пирамиды по высоте и площади основания

Формула расчета объема пирамиды, которая основана на ее высоте и площади основания, выглядит следующим образом:

V = 1/3 * S * h

где: V – объем пирамиды S – площадь основания пирамиды h – высота пирамиды

Для того, чтобы вычислить объем пирамиды, нужно знать ее высоту и площадь основания. Подставьте известные значения в соответствующие поля калькулятора и получите необходимое значение объема.

Например, для пирамиды с площадью основания 20см²и высотой 5см расчёт объема будет выглядеть таким образом:

V = 1/3 * S * h = 1/3 * 20 * 5 = 33.3см³

Как вычислить объем пирамиды с правильным многоугольным основанием

Правильная пирамида – это пирамида, в основании которой лежит правильный многоугольник, а высота проходит через центр вписанной в основание окружности.

Объем пирамиды с правильным многоугольным основанием можно вычислить по формуле:

V = (n * a² * h) / (12 * tan(180^о/n))

где h – высота пирамиды, а – сторона основания, n – количество сторон в основании

Например, объем правильной многоугольной пирамиды с высотой 100см, стороной основания 12см и количеством сторон 6 равен:

V = (n * a² * h) / (12 * tan(180^о/n)) = (6 * 12² * 100) / (12 * tan(180^о/6)) = 12470.7658см³

Как вычислить объем правильной треугольной пирамиды

Правильная треугольная пирамида – это пирамида, у которой основанием является равносторонний треугольник и грани равные равнобедренные треугольники.

Объем пирамиды с правильным треугольным основанием можно вычислить по формуле:

V = h * a² / 4 * √3

где h – высота пирамиды, а – сторона основания

Таким образом, чтобы вычислить объем правильной треугольной пирамиды, необходимо знать длину стороны основания и длину ее высоты, и затем использовать вышеуказанную формулу.

Например, объем правильной треугольной пирамиды с высотой 100см и стороной основания 12см равен:

V = h * a² / 4 * √3 = 100 * 12² / 4 * √3 = 2078.461см³

Как вычислить объем правильной четырехугольной пирамиды

Правильная четырехугольная пирамида – это пирамида, у которой основанием является квадрат и грани равные равнобедренные треугольники.

Объем пирамиды с правильным четырехугольным основанием можно вычислить по формуле:

V = 1 / 3 * h * a²

где h – высота пирамиды, а – сторона основания.

Например, объем правильной четырехугольной пирамиды с высотой 100см и стороной основания 12см равен:

V = 1 / 3 * h * a² = 1 / 3 * 100 * 12² = 4800см³

Как вычислить объем тетраэдра

Тетраэдр – пирамида, у которой все грани – равносторонние треугольники.

Объем пирамиды с правильным треугольным основанием можно вычислить по формуле:

V = a³ * √2 / 12

где а – сторона основания.

Таким образом, чтобы вычислить объем правильной треугольной пирамиды, необходимо знать длину стороны основания, и затем использовать вышеуказанную формулу.

Например, объем тетраэдра со стороной основания 12см равен:

V = a³ * √2 / 12 = 12³ * √2 / 12 = 203.6468см³

❓ Вопросы и ответы

А вот несколько ответов на часто задаваемы вопросе о пирамиде и ее параметрах.

Как найти площадь основания пирамиды?

Площадь основания пирамиды зависит от ее формы. Если основание пирамиды имеет форму прямоугольника, площадь вычисляется по формуле S = a * b, где a и b – длины сторон прямоугольника. Если основание пирамиды имеет форму треугольника, площадь вычисляется по формуле S = (a * b * sin(α)) / 2, где a и b – длины сторон треугольника, α – угол между ними.

Как определить высоту пирамиды?

Высоту пирамиды можно определить с помощью теоремы Пифагора. Для этого необходимо построить прямую, проходящую через вершину пирамиды и перпендикулярную к основанию. Затем нужно измерить длину этой прямой и длину отрезка, соединяющего середины двух сторон основания. Высота пирамиды равна квадратному корню из разности квадратов этих длин.

Как найти боковую поверхность пирамиды?

Боковая поверхность пирамиды состоит из треугольников, каждый из которых имеет общую вершину в вершине пирамиды и стороны, соединяющие эту вершину с точками на основании. Площадь каждого такого треугольника можно вычислить по формуле S = (a * h) / 2, где a – длина стороны основания, h – высота боковой грани. Общая площадь боковой поверхности пирамиды равна сумме площадей всех ее боковых граней.

Как вычислить полную поверхность пирамиды?

Для вычисления полной поверхности пирамиды нужно сложить площади всех ее боковых граней и площадь ее основания. Формула для вычисления площади боковой грани зависит от формы пирамиды. Например, если пирамида имеет правильную многоугольную основу, то ее боковые грани будут равными равнобедренными треугольниками. Площадь такой грани можно вычислить по формуле: Sбок = (1/2) * Периметр основания * Высота боковой грани, где Периметр основания – периметр многоугольной основы пирамиды, Высота боковой грани – расстояние от вершины пирамиды до середины ребра ее основания.

Советы

Об этой статье

Была ли эта статья полезной?

Video

References

About This Article

Did this article help you?

Содержание

меры

Метод 1 из 3: определение объема с учетом площади основания и высоты

Метод 2 из 3: определение объема по наклонной высоте

Метод 3 из 3. Определите объем, используя высоту границы

подсказки

TL; DR (слишком длинный; Не читал)

Советы

Что считает калькулятор

Где можно применить калькулятор объема пирамиды

В чем преимущество пирамиды

Как вычислить объем пирамиды

Как вычислить объем пирамиды по высоте и площади основания

Как вычислить объем пирамиды с правильным многоугольным основанием

Как вычислить объем правильной треугольной пирамиды

Как вычислить объем правильной четырехугольной пирамиды

Как вычислить объем тетраэдра

❓ Вопросы и ответы

Как найти площадь основания пирамиды?

Как определить высоту пирамиды?

Как найти боковую поверхность пирамиды?

Как вычислить полную поверхность пирамиды?

Похожие калькуляторы

Есть что добавить?

Добавить комментарий Отменить ответ

Советы

Об этой статье

Была ли эта статья полезной?

Video

References

About This Article

Did this article help you?

Содержание

меры

Метод 1 из 3: определение объема с учетом площади основания и высоты

Метод 2 из 3: определение объема по наклонной высоте

Метод 3 из 3. Определите объем, используя высоту границы

подсказки

TL; DR (слишком длинный; Не читал)

Советы

Что считает калькулятор

Где можно применить калькулятор объема пирамиды

В чем преимущество пирамиды

Как вычислить объем пирамиды

Как вычислить объем пирамиды по высоте и площади основания

Как вычислить объем пирамиды с правильным многоугольным основанием

Как вычислить объем правильной треугольной пирамиды

Как вычислить объем правильной четырехугольной пирамиды

Как вычислить объем тетраэдра

❓ Вопросы и ответы

Как найти площадь основания пирамиды?

Как определить высоту пирамиды?

Как найти боковую поверхность пирамиды?

Как вычислить полную поверхность пирамиды?

Похожие калькуляторы

Есть что добавить?

Вам также может понравиться

Как найти клиентов на портреты

Как найти затвердевшую окаменелость в террарии

Как найти в ворде стиралку

Добавить комментарий Отменить ответ