Найти массу, плотность или объем онлайн
На данной странице калькулятор поможет найти плотность, массу или объем вещества онлайн. Для расчета введите значения в калькулятор.
Объем, масса и плотность
Найти
Масса:
Объем:
Плотность:
Ответы:
Формула для нахождения массы тела через плотность и объем:
m – масса; V – объем; p – плотность.
Формула для нахождения объема тела через плотность и массу:
m – масса; V – объем; p – плотность.
Формула для нахождения плотности тела через объем и массу:
m – масса; V – объем; p – плотность.
Калькулятор
Формула массы через плотность и объем является одной из базовых формул физики, изучаемых в рамках школьной программы еще в седьмом классе. Она пригодится в решении многих задач.
Формула зависимости массы от объема и плотности
Для того, чтобы найти плотность жидкости или твердого вещества, существует базовая формула: плотность равна массе, поделенной на объем.
Записывается это так:
ρ = m / V
И из нее можно вывести еще две формулы.
Формулу для объема тела:
V = m / ρ
А также формулу для расчета массы:
m = V * ρ
Как видите, запомнить последнюю очень легко: это единственная формула, где две единицы нужно умножить.
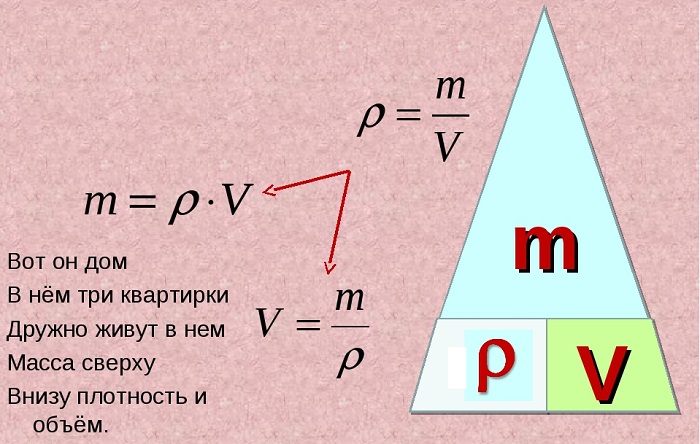
Для запоминания этой зависимости можно использовать рисунок в виде «пирамидки», разделенной на три секции, в вершине которой находится масса, а в нижних углах – плотность и объем.
Несколько иначе обстоят дела с газами. Рассчитать их вес гораздо сложнее, так как у газов нет постоянной плотности: они рассеиваются и занимают весь доступный им объем.
Для этого пригодится понятие молярной массы, которую можно найти, сложив массу всех атомов в формуле вещества при помощи данных из периодической таблицы.
Вторая единица, которая нам понадобится – количество вещества в молях. Его можно вычислить по уравнению реакции. Подробнее об этом можно узнать в рамках курса химии.
Другой способ нахождения мольного количества – через объем газа, который нужно поделить на 22,4 литра. Последнее число – это объемная постоянная, которую стоит запомнить.
В итоге, зная две предыдущие величины, мы можем определить массу газа:
m = n * M,
где M – это молярная масса, а n – количество вещества.
Результат получится в граммах, поэтому для решения физических задач важно не забыть перевести его в килограммы, поделив на 1000. Числа в этой формуле часто могут оказываться достаточно сложными, поэтому для вычислений может понадобиться калькулятор.
Еще один нестандартный случай, с которым можно столкнуться – необходимость найти плотность раствора. Для этого существует формула средней плотности, построенная аналогично формулам других средних величин.
Для двух веществ посчитать ее можно так:
(m1 + m2) / V1 + V2.
Также из этой формулы можно вывести несколько других в зависимости от того, какие из величин известны по условию задачи.
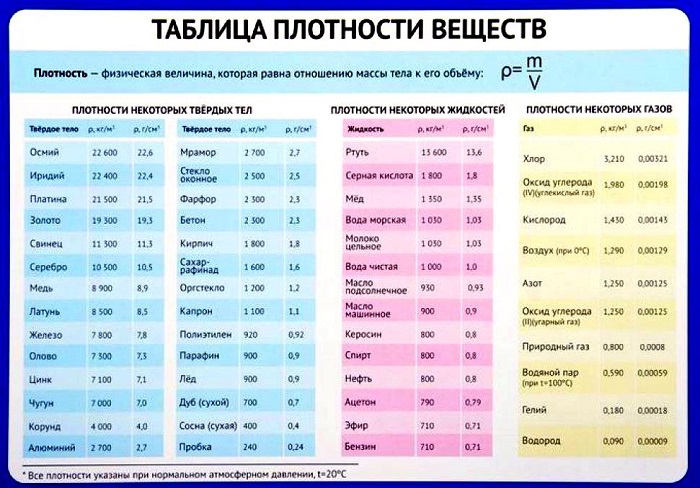
Таблица плотности некоторых веществ
Плотность многих веществ известна заранее и легко находится по соответствующей таблице.
В работе с ней важно обращать внимание на размерности и не забывать о том, что все данные собраны при нормальных условиях: комнатной температуре в 20 градусов Цельсия, а также определенном давлении, влажности воздуха и так далее.
Плотности других, более редких веществ можно найти онлайн.
Как минимум одно из значений плотности стоит запомнить, так как оно часто появляется в задачах. Это плотность воды – 1000 кг/м3 или 1 г/см3.
Примеры решения задач
Задача 1
Условие: имеется алюминиевый брусок со сторонами 3, 5 и 7 сантиметров. Какова его масса?
Решение:
Найдем объем бруска:
V = a * b * c;
V = 3 * 5 * 7 = 105 см3;
Табличное значение плотности алюминия: 2800 кг/м3 или 2,8 г/см3;
Вычислим массу бруска:
m = V * ρ;
m = 105 * 2,8 = 294 г.
Ответ: m = 294 г.
Задача 2
Задача по смежной теме.
Условие: сколько энергии потребуется для того, чтобы довести воду комнатной температуры (20 градусов Цельсия) из стакана (ёмкость 200 мл) до температуры кипения?
Решение:
Найдем недостающую информацию: температура кипения воды t2 = 100 градусов Цельсия, удельная теплоемкость воды с = 4200 Дж/кг * С, плотность воды 1 г/см3, 1 мл воды = 1 см3;
Найдем массу воды:
m = V * ρ;
m = 200 * 1 = 200 г = 0,2 кг;
Найдем энергию:
Q = c * m * (t2 – t1);
Q = 4200 * 0,2 * (100 – 20) = 67200 Дж = 67,2 кДж.
Ответ: Q = 67,2 кДж.
Задача 3
Задача с молярной массой.
Условие: найдите массу CO2 при объеме в 5,6 л.
Решение:
Найдем молярную массу CO2 :
M = 12 + 16 * 2 = 44 г/моль;
Найдем количество вещества через объем:
n = 5,6 / 22,4 = 0,25 моль;
Найдем массу:
m = n * M;
m = 0,25 * 44 = 11 г.
Ответ: m = 11 г.
Содержание:
- § 1 Расчет массы и объема вещества по его плотности
- § 2 Решение задач
- § 3 Важно запомнить
§ 1 Расчет массы и объема вещества по его плотности
В этом уроке мы изучим, как можно определить массу и объем тела, если известна плотность вещества.
Плотность – скалярная физическая величина, показывающая, чему равна масса вещества, взятого в объеме 1 м3, и равная отношению массы тела к его объему: p = m : v.
Из формулы плотности следует, что масса тела равна произведению плотности вещества на объем этого тела: m = ρ · V.
Чтобы вычислить объем тела, нужно массу тела разделить на его плотность: v = m : p.
Для правильного решения задач нужно уметь верно переводить единицы измерения величин в Международную систему единиц: 1 г = 0,001 кг, 1 л = 1 дм3 = 0,001 м3, 1 см3 = 0,000 001 м3, 1 г/см3 = 1000 кг/м3.
§ 2 Решение задач
Какова масса подсолнечного масла в бутылке объемом 3 л, если плотность масла равна 930 кг/м3?
Запишем условие задачи. Нам известны объем бутылки (обозначается буквой V) 3 л, и плотность подсолнечного масла (обозначается буквой ρ) 930 кг/м3. Выразим объем бутылки в Международной системе единиц. 1 л = 0,001 м3, следовательно, 3 л составляют 0,003 м3.
Решение: Чтобы найти массу тела, нужно плотность умножить на объем: m = ρ · V. Подставим числовые значения величин: 930 кг/м3 · 0,003 м3 = 2,79 кг.
Сколько штук строительного кирпича размером 250 мм х 120 мм х 65 мм допускается перевозить на автомашине грузоподъемностью 4 т? Плотность кирпича 1800 кг/м3.
Запишем условие задачи и выразим данные в Международной системе единиц. Известны размеры кирпича: длина а = 250 мм = 0,25 м, ширина b= 120 мм = 0,12 м, высота с = 60 мм = 0,06 м, плотность кирпича ρ = 1800 кг/м3, грузоподъемность – наибольшая масса груза, которую может перевезти автомобиль – m = 4 т = 4000 кг. Найти количество кирпичей – обозначим латинской буквой N.
Решение: Количество кирпичей можно найти, поделив общую массу всех кирпичей на массу одного кирпича: N = m/m1. Чтобы найти массу одного кирпича, нужно плотность умножить на его объем: m1 = ρ · V. Кирпич имеет форму прямоугольного параллелепипеда, следовательно, его объем равен произведению длины, ширины и высоты кирпича. Подставим числовые значения известных величин и вычислим. Объем кирпича равен 0,0018 м3. Масса одного кирпича m1 равна 1800 кг/м3 , умножим на 0,0018 м3 , равно 3,24 кг. Тогда число кирпичей равно N 4000 кг, разделим на 3,24 кг и получим 1234, 567 штук или число целых кирпичей 1234 штуки.
Медный шар имеет массу 840 г при объеме 120 см3. Сплошной этот шар или полый? Плотность меди 8900 кг/м3.
Запишем условие задачи. Известна масса шара m 840 г, что в системе СИ составляет 0,84 кг, объем шара V=120 см3, в СИ 0,00 012 м3, плотность меди ρ = 8900 кг/м3. Определить, сплошной шар или содержит внутри пустое пространство?
Решение. Представим, что на рычажных весах лежат два медных шара, один сплошной, второй содержит внутри пустое пространство, то есть полый шар. Если у них массы одинаковы, то объем полого шара должен быть больше, чем объем сплошного шара (рис 1).
Определим, каков объем шара, состоящего полностью из меди. Если объем окажется равным 120 см3, то шар сплошной и пустот не содержит. Если же вычисленный объем окажется меньше 120 см3, значит, внутри есть полость.
Чтобы найти объем сплошного медного шара, массу шара разделим на его плотность. Для упрощения проведем вычисления в граммах и кубических сантиметрах.
§ 3 Важно запомнить
Плотность – скалярная физическая величина, показывающая, чему равна масса вещества, взятого в объеме 1 м3, и равная отношению массы тела к его объему: p = m : v.
Масса тела равна произведению плотности вещества на объем этого тела: m = ρ · V.
Чтобы вычислить объем тела, нужно массу тела разделить на его плотность: V = m : p.
Список использованной литературы:
- Волков В.А. Поурочные разработки по физике: 7 класс. – 3-е изд. – М.: ВАКО, 2009. – 368 с.
- Волков В.А. Тесты по физике: 7-9 классы. – М.: ВАКО, 2009. – 224 с. – (Мастерская учителя физики).
- Кирик Л.А. Физика -7. Разноуровневые самостоятельные и контрольные работы. – М.: Илекса, 2008. – 192 с.
- Контрольно-измерительные материалы. Физика: 7 класс / Сост. Зорин Н.И. – М.: ВАКО, 2012. – 80 с.
- Марон А.Е., Марон Е.А. Физика. 7 Дидактические материалы. – М.: Дрофа, 2010. – 128 с.
- Перышкин А.В. Физика. 7 класс – М.: Дрофа, 2011.
- Тихомирова С.А. Физика в пословицах и поговорках, стихах и прозе, сказках и анекдотах. Пособие для учителя. – М.: Новая школа, 2002. – 144 с.
Использованные изображения:
Плотность тела — зависимость массы и объема
Например, железный куб с ребром 10 см имеет массу 7,8 кг, алюминиевый куб тех же размеров имеет массу 2,7 кг, а масса такого же куба изо льда 0,9 кг. Величина, характеризующая массу, приходящуюся на единичный объём данного вещества, называется плотностью. Плотность равна частному от массы тела и его объёма, т.е.
ρ = m/V, где ρ (читается «ро») плотность тела, m — его масса, V объём.
В Международной системе единиц СИ плотность измеряется в килограммах на кубический метр (кг/м3); также часто используются внесистемные единицы, например, грамм на кубический сантиметр (г/см3). Очевидно, 1 кг/м3 = 0,001 г/см3. Заметим, что при нагревании веществ их плотность уменьшается или (реже) увеличивается, но это изменение так незначительно, что при расчётах им пренебрегают.
Сделаем оговорку, что плотность газов непостоянна; когда говорится о плотности какого-нибудь газа, обычно имеется ввиду его плотность при 0 градусов по Цельсию и нормальном атмосферном давлении (760 миллиметров ртутного столба).
Определение массы и плотности жидкостей
Определение массы жидкостей, кроме непосредственного взвешивании. — с известной погрешностью можно производить объемным методом — с помощью пипеток, бюреток, мерных цилиндров, колб, мензурок и т. п. по формуле:
m = Vp
где m — масса жидкости, г; V — ее объем, см3; р—плотность жидкости, г/см3.
Плотность жидкостей и растворов находят по справочным таблицам или определяют самостоятельно. В лабораторной практике наибольшее распространение получили два метода определения плотности: 1) определение степени погружения денсиметра з жидкость; 2) взвешивание жидкости в сосуде известного объема.
При определении плотности с помощью денсиметр а последний погружают в цилиндр с жидкостью, термостатированной при определенной температуре, обычно при 20 или 15 °С. (рис. 25).
Для измерения температуры жидкости используют термометр с ценой деления не менее 0,5°С: неточность в измерении температуры в 1°С дает ошибку в значении плотности до 0,1%. Шкала денсиметров проградупрозана непосредственно в единицах плотности. Значение плотности жидкости считывают по делению шкалы, находящемуся на одном уровне с мениском жидкости.
Рис. 21. Определение плотности жидкости с помощью денсиметра.
Цена деления таких денсиметров 0,001 г/см3, а весь набор охватывает интервал плотностей от 0,700 до 1,840 г/см3. Иногда удобнее пользоваться приборами, шкала которых проградуирована в единицах концентрации для растворов определенных веществ. Такие приборы принято называть ареометрами.
В тех случаях, когда количество жидкости, находящейся в распоряжении экспериментатора, слишком мало, ее плотность определяют посредством пикнометров— небольших (от 1 до 100 мл) мерных колб.
На каждый находящийся в работе пикнометр должен быть нанесен номер титановым карандашом и заведена индивидуальная карточка, в которую закосят его точную массу (взвешивают чистый сухой пикнометр вместе с пробкой на аналитических весах) и значение «водной константы». Водная константа — эта масса воды в объеме пикнометра, приведенная к массе воды при 4 °С (температура, при которой плотность воды равна 1 г/см3).
С целью определения водной константы нового пикнометра его тщательно моют и заполняют предварительно прокипяченной (для удаления растворенного воздуха) дистиллированной водой немного выше метки.
Наполненный пикнометр выдерживают в течение 20 мин в водяном термостате при 20°С, после чего с помощью капилляра или тонких полосок фильтровальной бумаги отбирают лишнюю воду, доводя ее уровень в шейке пикнометра до метки по нижнему краю мениска. Верхнюю часть шейки пикнометра и шлиф протирают досуха кусочком фильтровальной бумаги, закрывают пикнометр пробкой, тщательно вытирают его снаружи, обсушивают 20—25 мин, после чего взвешивают на аналитических весах. Вычитая из массы пикнометра с водой массу сухого пикнометра получают массу воды в объеме пикнометра при 20 °С. Частное от деления полученного значения на 0,99823 г (масса 1 мл воды при 20 °С) и есть водная константа пикнометра.
При определении плотности какой-либо жидкости проделывают тс же операции, что и при определении водной константы. Для вычисления относительной плотности вещества d массу жидкости в объеме данного пикнометра делят на величину его водной константы
К оглавлению
см. также
- Правила работы с весами
- Определение массы и плотности жидкостей
Расчет массы и объема тела
В повседневной жизни мы часто сталкиваемся с необходимостью рассчитывать массы и объёмы разных тел. Это удобно делать, применяя плотность.
Плотности разных веществ определяются по таблицам, например, плотность воды 1000 кг/м3, плотность этилового спирта 800 кг/м3.
Из определения плотности следует, что масса тела равна произведению его плотности и объёма. Объём же тела равен частному от массы и плотности. Этим пользуются при расчётах:
m = ρ * V; или V = m / p;
гдн m масса данного тела, ρ его плотность, V объём тела.
Как найти массу воды: узнай все
#1
Вода является источником жизни, одним из самых распространённых элементов в природе. Тем не менее, она остаётся самым важным соединением на планете, содержится в каждом живом организме. Кроме того, также она есть и во многих неорганических смесях и препаратах, используемых на производстве. Часто становится актуален вопрос как найти массу воды в определённой ёмкости или предмете, рассчитать её массовую долю.
#2
Массовая доля — отношение массы вещества ко всему весу тела. Например, организм человека на две трети состоит из воды, а огурец — на 90 %. Это значит, что в теле массой 75 килограммов, содержится 50 литров воды. Переходя к вопросу как перевести объём в массу, необходимо разобраться с таким понятием, как плотность вещества. Плотность является скалярной величиной и определяется как отношение веса к объёму.
#3
Также плотность определяется через количество вещества. Для этого необходимо, как рассчитать молярную массу, так и количество вещества. Рассмотрим пример: арбуз на 80% состоит из жидкости, объём арбуза 5 литров. Сколько килограммов воды в данном арбузе. Сначала вычислим объём воды в арбузе. 5 литров * 0,8 (это 80 %) = 4 литра. Теперь остаётся вычислить массу 4-х литров воды. Плотность воды составляет 1 кг/литр, следовательно 4 л * 1 кг/л = 4 кг. Ответ: 4 килограмма.
#4
Зная, как найти массу через плотность, можно вычислить не только массу воды, но и массу других веществ. Достаточно знать плотность необходимого элемента, для этого существуют специальные таблицы плотностей. Решим обратную задачу. Стальной брусок имеет массу 1 кг. Вычислить его объём. Для этого воспользуемся таблицей, установим плотность стали (7,8 кг/литр) . Далее разделим массу на объём, получим 1 (кг) / 7,8 (кг/литр) = 0,8 литра.
#5
Также может возникнуть задача, как найти массу, зная объем неоднородного вещества. Решим такую задачу. Трёхлитровую ёмкость полностью наполнили водой и ацетоном в соотношении 3 к 1. Вычислить массу полученной смеси, массой ёмкости пренебречь. Для начала, выясним какой объём воды и ацетона. Если соотношение было 3 к 1, то необходимо разделить всю ёмкость на 3+1 = 4 части. 3 литра / 4 = 0,5 литра приходится на одну часть.
#6
Следовательно, воды будет 3 * 0,5 = 2,5 литра, а ацетона 1*0,5 = 0,5 литра. Теперь можно приступить к вычислению масс. Плотность воды нам уже известна (1 кг/литр) , плотность ацетона, согласно таблице равна 0,8 кг/литр. Далее вычисляем массу воды: 2,5 литра * 1 кг/литр = 2,5 кг; и ацетона: 0.5 литра * 0,8 кг/литр = 0,6 кг. Сложим полученные результаты: 2,5 + 0,6 = 2.5 килограммов. Задаче решена.
Рассмотрим более сложный пример расчета
Слиток из двух металлов с плотностями ρ1 и ρ2 , имеет массу m и объём V. Определить объём этих металлов в слитке.
Решение. Пусть V1 объём первого металла, V2 объём второго металла. Тогда V1 + V2 = V; V1 = V V2; ρ1V1 + p2V2 = ρ1V1 + ρ2 (V V1) = m
Решив это уравнение относительно V1 , получаем:
V1= (m ρ2V)/(ρ1 ρ2)
Теперь найдём V2:
V2= V — (m ρ2V)/(ρ1 ρ2)
Ответ: объём первого тела равен (m ρ2V)/(ρ1 ρ2), второго V — (m ρ2V)/( ρ1 ρ2). Заметим, однако, что при ρ1 = ρ2 задача не имеет однозначного решения.
Формула зависимости массы от объема и плотности
Для того, чтобы найти плотность жидкости или твердого вещества, существует базовая формула: плотность равна массе, поделенной на объем.
Записывается это так:
И из нее можно вывести еще две формулы.
Формулу для объема тела:
А также формулу для расчета массы:
Как видите, запомнить последнюю очень легко: это единственная формула, где две единицы нужно умножить.
Для запоминания этой зависимости можно использовать рисунок в виде «пирамидки», разделенной на три секции, в вершине которой находится масса, а в нижних углах – плотность и объем.
Несколько иначе обстоят дела с газами.
Рассчитать их вес гораздо сложнее, так как у газов нет постоянной плотности: они рассеиваются и занимают весь доступный им объем.
Для этого пригодится понятие молярной массы, которую можно найти, сложив массу всех атомов в формуле вещества при помощи данных из периодической таблицы.
Вторая единица, которая нам понадобится – количество вещества в молях. Его можно вычислить по уравнению реакции. Подробнее об этом можно узнать в рамках курса химии.
Другой способ нахождения мольного количества – через объем газа, который нужно поделить на 22,4 литра. Последнее число – это объемная постоянная, которую стоит запомнить.
В итоге, зная две предыдущие величины, мы можем определить массу газа:
где M – это молярная масса, а n – количество вещества.
Результат получится в граммах, поэтому для решения физических задач важно не забыть перевести его в килограммы, поделив на 1000. Числа в этой формуле часто могут оказываться достаточно сложными, поэтому для вычислений может понадобиться калькулятор.
Еще один нестандартный случай, с которым можно столкнуться – необходимость найти плотность раствора
. Для этого существует формула средней плотности, построенная аналогично формулам других средних величин.
Для двух веществ посчитать ее можно так:
Также из этой формулы можно вывести несколько других в зависимости от того, какие из величин известны по условию задачи.
Формула зависимости массы от объема и плотности
Для того, чтобы найти плотность жидкости или твердого вещества, существует базовая формула: плотность равна массе, поделенной на объем.
Записывается это так:
И из нее можно вывести еще две формулы.
Формулу для объема тела:
А также формулу для расчета массы:
Как видите, запомнить последнюю очень легко: это единственная формула, где две единицы нужно умножить.
Для запоминания этой зависимости можно использовать рисунок в виде «пирамидки», разделенной на три секции, в вершине которой находится масса, а в нижних углах – плотность и объем.
Несколько иначе обстоят дела с газами.
Рассчитать их вес гораздо сложнее, так как у газов нет постоянной плотности: они рассеиваются и занимают весь доступный им объем.
Вес делить на плотность
Письмо с инструкцией по восстановлению пароля будет отправлено на вашу почту
В этом уроке мы изучим, как можно определить массу и объем тела, если известна плотность вещества.
Плотность – скалярная физическая величина, показывающая, чему равна масса вещества, взятого в объеме 1 м3, и равная отношению массы тела к его объему: p = m : v.
Из формулы плотности следует, что масса тела равна произведению плотности вещества на объем этого тела: m = ρ · V.
Чтобы вычислить объем тела, нужно массу тела разделить на его плотность: v = m : p.
Для правильного решения задач нужно уметь верно переводить единицы измерения величин в Международную систему единиц: 1 г = 0,001 кг, 1 л = 1 дм3 = 0,001 м3, 1 см3 = 0,000 001 м3, 1 г/см3 = 1000 кг/м3.
Какова масса подсолнечного масла в бутылке объемом 3 л, если плотность масла равна 930 кг/м3?
Запишем условие задачи. Нам известны объем бутылки (обозначается буквой V) 3 л, и плотность подсолнечного масла (обозначается буквой ρ) 930 кг/м3. Выразим объем бутылки в Международной системе единиц. 1 л = 0,001 м3, следовательно, 3 л составляют 0,003 м3.
Решение: Чтобы найти массу тела, нужно плотность умножить на объем: m = ρ · V. Подставим числовые значения величин: 930 кг/м3 · 0,003 м3 = 2,79 кг.
Сколько штук строительного кирпича размером 250 мм х 120 мм х 65 мм допускается перевозить на автомашине грузоподъемностью 4 т? Плотность кирпича 1800 кг/м3.
Запишем условие задачи и выразим данные в Международной системе единиц. Известны размеры кирпича: длина а = 250 мм = 0,25 м, ширина b= 120 мм = 0,12 м, высота с = 60 мм = 0,06 м, плотность кирпича ρ = 1800 кг/м3, грузоподъемность – наибольшая масса груза, которую может перевезти автомобиль – m = 4 т = 4000 кг. Найти количество кирпичей – обозначим латинской буквой N.
Масса через плотность и объем, формула
Масса тела выражается через плотность и объем следующей формулой:
Масса тела — есть произведение плотности вещества из которого состоит тело на его объем.
[ m = ρV ]
Здесь:
V — объем тела (м³),
m — масса тела, (килограмм),
ρ — плотность вещества, (кг/м³).
Вычислить, найти массу твердых тел или жидкостей через плотность и объем по формуле (1)
Выберите вещество ▼
| ρ (плотность вещества, x103 кг/м³) |
| V (объем тела, м³) |
Вычислить
нажмите кнопку для расчета
Вычислить, найти массу газа через плотность и объем по формуле (1)
Выберите вещество ▼
| ρ (плотность газа, кг/м³) |
| V (объем газа, м³) |
Вычислить
нажмите кнопку для расчета
Масса через плотность и объем |
стр. 443 |
|---|