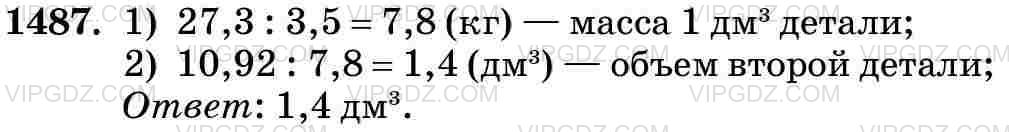Как найти объем металлической детали

1. Расчет обЪема и веса детали

На рисунке 1
приведена схема разбивки детали на
элементарные объемы. Объем детали будет
равен алгебраической сумме элементарных
объемов.

Рисунок 1 – Схема
разбивки детали на элементарные объемы

Рассмотрим элемент,
объем которого мы можем найти по формуле
(1)

V_Ι
= V₁-V_А-V_В–
V_С-V_Д-V_Е-V_Ж
V_З ,
(1)

где
объем V₁
– объем полого цилиндра:

V_{пол.
цил.} = 0,785 ∙
h
∙ (D²
– d²),
(2)

V₁=0,785∙
34 ∙ (192,776²
– 97²)=740743,22
мм³

объем V_А
– объем четверти тора:

V_А=2,47r²(D-0,848r),
(3)

V_А=2,47∙10²((97+20)-0,848∙10)=26804,44мм³

объем V_В
– объем
четверти тора:

V_В=2,47r²(D+0,848r),
(4)

V_В=2,47∙10²((172-20)+0,848∙10)=39638,56мм³

объем V_С
– объем полового цилиндра, находим по
формуле (2)

V_С=0,785∙10²(152²-117²)=
73907,75 мм³

объем V_Д
– объем
восьми отверстий, имеющих форму цилиндра:

V_цил.
= 0,785∙h∙D²,
(5)

V_Д=8∙0,785∙7∙9²=3560,76
мм³

объем V_Е
– объем восьми отверстий, имеющих форму
усеченного конуса:

V_Е=
H(D²+Dd+d²),
(6)

V_Е
=
∙3(15²+15∙9+9²)=2769,48мм³

объем V_ж–
объем полового цилиндра, находим по
формуле (2)

V_ж=0,785∙14(175²+113²)
= 6237,44 мм³

объем V_з
– объем четверти тора, находится по
формуле (4)

V_з
= 19596,58 мм³

V_Ι
= 378228,20 мм³

Рассмотрим второй
элемент, объем которого мы можем найти
по формуле (6)

V_ΙΙ
= V₂-V_К-V_И
, (7)

где
объем V₂–
объем цилиндра, находим по формуле (5)

V₂
= 0,785∙97²∙56=413619,64
мм³

объем V_К–
объем цилиндра, находим по формуле (5)

V_К
= 0,785∙77²∙56=260638,84
мм³

объем V_И–
объем двух конических кольца:

V_И
= 0,524(3D-2d)dH
, (8)

V_И
= 2∙0,524(3∙97-2∙3,5)3,5∙11=11458,83 мм³

V_ΙΙ=141521,97
мм³

Рассмотрим третий
элемент объем, которого V_ΙΙΙ
– это объем зубьев колеса, и он равен
объему полого цилиндра (формула (2)),
умноженному на коэффициент, равный
0,55:

V_ΙΙΙ
=∙0,55 0,785∙34(210,78²
– 192,78²)
= 106655,70мм³,
(9)

Складывая объемы
трех этих элементов найденные по формулам
(1), (7), (9) получим объем всей детали:

V_Д
= V_Ι+V_ΙΙ+V_ΙΙΙ ,
(10)

где
V_Д– объем детали;

V_Ι
,V_ΙΙ,V_ΙΙΙ
– объемы,
получаемые по формулам (1,7,9).

V_Д=
626405,87 мм³
= 626,406 см³

Теперь, зная объем
детали, найдем массу детали по формуле
(11):

М_Д
= V_Д
∙ ρ,
(11)

где
ρ
– плотность материала,
=7,8
г/см³.

М_Д
= 626,406 ∙ 7,8 = 4917,29 г

1. Определение группы металла , группы сложности , группы точности , исходного индекса

Расчет ведем по
ГОСТ 7505-89.

Группа стали
назначается, исходя из среднего массового
содержания углерода или легирующих
элементов. Материал – Cталь
20ХН3А ГОСТ 4543-71, суммарная массовая доля
легирующих элементов 4%, а значит группа
стали М2.

Степень сложности
определяется путем вычисления следующего

отношения
(11):

С_i
=
,
(12)

где
V_ПОК
– объем поковки;

V_Ф
– объем геометрической фигуры, в которую
вписывается форма детали (рисунок 2).

Рисунок 2 –
Геометрическая фигура, в которую
вписывается форма детали

Для
данной детали описанной фигурой будет
являться цилиндр, размеры которого
увеличены на 1,05. Найдем объем этого
цилиндра по формуле (2):

V_Ф
= 0,785 ∙ 58,8 ∙ 221,32²
= 2260936,19 (мм³).

Объем
поковки на данном этапе находится по
формуле (13):

V_ПОК
= V_Д
∙
К_Р,
(13)

где
К_Р
– расчетный коэффициент, К_Р
= 1,7.

V_ПОК
=626405,87
∙ 1,7 = 1064889,97 (мм³).

С_i
=
= 0,47.

По
расчету получаем степень сложности
поковки С₂.

Класс
точности поковки устанавливается в
зависимости от технологического процесса
и оборудования для ее изготовления, а
также исходя из предъявляемых требований
к точности размеров поковки. Согласно
ГОСТ 7505-89 выбираем
4-й класс точности
– Т4.

Массу
поковки найдем по формуле, аналогичной
формуле (11):

М_ПОК
= 1064,889 ∙ 7,8 = 8306,1 г

Исходный
индекс для последующего назначения
основных припусков, допусков и допускаемых
отклонений определяется в зависимости
от массы, марки стали, степени сложности
и класса точности поковки по ГОСТ
7505-89.
В данном случае исходный индекс
14.

ГДЗ и решебники
вип уровня