Объёмы многогранников
Куб
V = a3 , где а — ребро куба

Прямоугольный параллелепипед
V = a * b * c, где a, b, c — рёбра фигуры: высота, ширина и длина

Параллелепипед
V = Sоснования * h, где h — высота параллепипеда.

Призма
V = Sоснования * h, где h — высота призмы

Пирамида
V = 1/3 Sоснования * h, где h — высота пирамиды


Объёмы тел вращения
Цилиндр
V = πR2h, где R — радиус основания, h — высота
Конус
V = 13 Sоснования * h
Шар
V = 43πR3 , где R — радиус шара

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Многогранники
Многогранник – это поверхность, составленная из многоугольников, ограничивающая некоторое геометрическое тело.
В данной теме мы рассмотрим составные многогранники (многогранники, состоящие обычно из нескольких параллелепипедов).
Объемы различных многогранников:
- Призма $V=S_{осн}·h$
- Пирамида $V={1}/{3}S_{осн}·h$
- Параллелепипед $V=a·b·c$, где $a, b$ и $c$ – длина, ширина и высота.
- Куб $V=а^3$, где $а$ – сторона куба
Задачи на нахождение объема составного многогранника:
- Первый способ.
- Составной многогранник надо достроить до полного параллелепипеда или куба.
- Найти объем параллелепипеда.
- Найти объем лишней части фигуры.
- Вычесть из объема параллелепипеда объем лишней части.
Пример:
Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).
Решение:
1. Достроим составной многогранник до параллелепипеда.
Найдем его объем. Для этого перемножим все три измерения параллелепипеда:
$V=10·9·4=360$
2. Найдем объем лишнего маленького параллелепипеда:
Его длина равна $9-4=5$
Ширина равна $4$
Высота равна $7$
$V=7·4·5=140$
3. Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:
$V=360-140=220$
Ответ: $220$
- Второй способ
- Разделить составной многогранник на несколько параллелепипедов.
- Найти объем каждого параллелепипеда.
- Сложить объемы.
Задачи на нахождение площади поверхности составного многогранника.
– Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:
$S_{полн.пов.}=P_{осн}·h+2S_{осн}$
Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.
Пример:
Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
Представим данный многогранник как прямую призму с высотой равной $12$.
$S_{полн.пов.}=P_{осн}·h+2S_{осн}$
$P_{осн}=8+6+6+2+2+4=28$
Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:
$S_1=6·6=36$
$S_2=2·4=8$
$S_осн=36+8=44$
Далее подставим все данные в формулу и найдем площадь поверхности многогранника
$S_{полн.пов.}=28·12+2·44=336+88=424$
Ответ: $424$
– Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.
Задачи на нахождение расстояния между точками составного многогранника.
В данных задачах приведены составные многогранники, у которых двугранные углы прямые. Надо соединить расстояние между заданными точками и достроить его до прямоугольного треугольника. Далее остается воспользоваться теоремой Пифагора для нахождения нужной стороны.
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$АС^2+ВС^2=АВ^2$
Задачи на нахождение угла или значения одной из тригонометрических функций обозначенного в условии угла составного многогранника.
Так как в данных задачах приведены составные многогранники, у которых все двугранные углы прямые, то достроим угол до прямоугольного треугольника и найдем его значение по тригонометрическим значениям.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$:
Для острого угла $В: АС$ – противолежащий катет; $ВС$ – прилежащий катет.
Для острого угла $А: ВС$ – противолежащий катет; $АС$ – прилежащий катет.
- Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Задачи на рассмотрение подобия фигур.
При увеличении всех линейных размеров многогранника в $k$ раз, площадь его поверхности увеличится в $k^2$ раз.
При увеличении всех линейных размеров многогранника в $k$ раз, его объём увеличится в $k^3$ раз.
Формулы объёма и площади поверхности. Многогранники.
Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:
- Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
- Элементарная логика.
Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.
 Куб |
|
|
 Параллелепипед |
|
|
 Прямоугольный параллелепипед |
|
|
 Призма |
|

|
 Пирамида |
|

|
Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».
Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.
Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.
Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.
Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.
Задача 1.Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Решение:

Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб 🙂
Очевидно, их 6, поскольку у куба 6 граней.
Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше – читайте о приемах решения задач по стереометрии.
Разберем задачи, где требуется найти площадь поверхности многогранника.
Мы рассмотрим призмы и пирамиды. Начнем с призмы.
Площадь полной поверхности призмы можно найти как сумму площадей всех ее граней. А это площади верхнего и нижнего оснований плюс площадь боковой поверхности.
Площадь боковой поверхности призмы – это сумма площадей боковых граней, которые являются прямоугольниками. Она равна периметру основания, умноженному на высоту призмы.

Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.
Многогранник на рисунке – это прямая призма с высотой 12.


Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:
(больший квадрат),
(маленький прямоугольник),
Подставим все данные в формулу:  и найдем площадь поверхности многогранника:
и найдем площадь поверхности многогранника:
Ответ: 424.
Задача 3. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).

Решение.

Перевернем многогранник так, чтобы получилась прямая призма с высотой 1.
Площадь поверхности этой призмы находится по формуле:


Найдем площадь основания. Для этого разделим его на два прямоугольника и посчитаем площадь каждого:
(большой прямоугольник),
(маленький прямоугольник).
Найдем площадь полной поверхности: 
Ответ: 54
Задача 4.Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.
Покажем еще один способ решения задачи.
Посмотрим, как получился такой многогранник. Можно сказать, что к «кирпичику», то есть прямоугольному параллелепипеду со сторонами 4, 1 и 3, сверху приклеен «кубик», все стороны которого равны 1.
И значит, площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольного параллелепипеда со сторонами 4,1,3 и
куба со стороной 1, без удвоенной площади квадрата со стороной 1:
Почему мы вычитаем удвоенную площадь квадрата? Представьте себе, что нам надо покрасить это объемное тело. Мы красим все грани параллелепипеда, кроме квадрата на верхней его грани, где на него поставлен кубик. И у куба мы покрасим все грани, кроме этого квадрата.
Ответ: 42
Задача 5. . Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 120° между ними. Наибольшая из площадей боковых граней равна 35 см². Найдите площадь боковой поверхности призмы.

Решение.
Пусть АВ = 5 см, ВС = 3 см, тогда
Из по теореме косинусов найдем ребро АС:
Отрезок АС – большая сторона , следовательно,
большая боковая грань призмы.
Поэтому или
откуда

Ответ: 75
Теперь две задачи на площадь боковой поверхности пирамиды.
Задача 6. Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13, ВС = 10; ребро АD перпендикулярно к плоскости основания и равно 9. Найдите площадь боковой поверхности пирамиды.

Решение.
Площадь боковой поверхности пирамиды – это сумма площадей всех ее боковых граней.
Проведем , тогда
(по теореме о 3-х перпендикулярах), то есть DК – высота треугольника DВС.
– равнобедренный (по условию АВ = АС), то высота АК, проведенная к основанию ВС, является и медианой, то есть ВК = КС = 5.
Из прямоугольного получим:
Из прямоугольного имеем:
(по двум катетам), тогда
следовательно


Ответ: 192
Задача 8. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 37. Найдите площадь поверхности пирамиды.

Решение:
Так как четырехугольная пирамида правильная, то в основании лежит квадрат, а все боковые грани – равные равнобедренные треугольники.
Площадь поверхности пирамиды равна

где р – полупериметр основания, h – апофема (высота боковой грани правильной пирамиды), a – сторона основания.
Значит, полупериметр основания .
Апофему найдем по теореме Пифагора:
Ответ: 2256
Как решать задачи на нахождение объема многогранника сложной формы?
Покажем два способа.
Первый способ
1.Составной многогранник достроить до полного параллелепипеда или куба.
2.Найти объем параллелепипеда.
3.Найти объем лишней части фигуры.
4.Вычесть из объема параллелепипеда объем лишней части.
Второй способ.
1.Разделить составной многогранник на несколько параллелепипедов.
2.Найти объем каждого параллелепипеда.
3.Сложить объемы.
Задача 9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

1) Достроим составной многогранник до параллелепипеда.
2) Найдем объем параллелепипеда – для этого перемножим его длину, ширину и высоту:
3) Найдем объем лишней части, то есть маленького параллелепипеда.
Его длина равна 9 – 4 = 5, ширина 4, высота 7, тогда его объем
4) Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:
Ответ: 220.
Задача 10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.

Объем призмы равен , а так как призма прямая, то ее боковое ребро является и высотой, то есть
Основанием призмы является прямоугольный треугольник c катетами 6 и 7, тогда площадь основания
Ответ: 126
Задача 11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 324 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, у которого сторона в 9 раз больше, чем у первого? Ответ выразите в сантиметрах.

Решение.
Объем призмы равен
Воду перелили в другой такой же сосуд. Это значит, что другой сосуд также имеет форму правильной треугольной призмы, но все стороны основания второго сосуда в 9 раз больше, чем у первого.
Основанием второго сосуда также является правильный треугольник. Он подобен правильному треугольнику в основании первого сосуда. Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Если все стороны треугольника увеличить в 9 раз, его площадь увеличится в раз. Мы получили, что площадь основания второго сосуда в 81 раз больше, чем у первого.
Объем воды не изменился, Так как
высота воды
должна быть в 81 раз меньше, чем
Она равна
(см).
Ответ: 4
Задача 12. Объем параллелепипеда Найдите объем треугольной пирамиды

Решение.
Опустим из вершины высоту
Н на основание



Диагональ основания делит его на два равных треугольника, следовательно,
Имеем:
Ответ: 3,5
Задача 13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 8, а высота равна

Решение.
По формуле объема пирамиды,  .
.
В основании пирамиды лежит правильный треугольник. Его площадь равна
Объем пирамиды
Ответ: 96
Задача 14. Через середины сторон двух соседних ребер основания правильной четырехугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объем меньшей из частей, на которые эта плоскость делит призму, если объем призмы равен 32.

Решение.
По условию, призма правильная, значит, в ее основании лежит квадрат, а высота равна боковому ребру.
Пусть тогда
Так как точки М и К – середины АD и DС соответственно, то
Площадь треугольника MDK, лежащего в основании новой призмы, составляет часть площади квадрата в основании исходной призмы.
Высоты обеих призм одинаковые. Согласно формуле объема призмы: , и значит, объем маленькой призмы в 8 раз меньше объема большой призмы. Он равен
Ответ: 4
Докажем полезную теорему.
Теорема: Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.
Доказательство:

Плоскость перпендикулярного сечения призмы перпендикулярна к боковым ребрам, поэтому стороны перпендикулярного сечения призмы являются высотами параллелограммов.
Больше задач на формулы объема и площади поверхности здесь.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Формулы объёма и площади поверхности. Многогранники.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023

Как найти объем многогранника
Прежде всего определимся, что же такое многогранник. Это трехмерная геометрическая фигура, грани которой представлены в виде плоских многоугольников. Единой формулы поиска объема многогранника не существует, так как многогранники бывают разной формы. Для того чтобы найти объем сложного многогранника, его условно делят на несколько простых, таких как параллелепипед, призма, пирамида, а затем складывают объемы простых многогранников и получают в результате искомый объем фигуры.
1
Как найти объем многогранника – параллелепипеда
Для начала найдем площадь прямоугольного параллелепипеда. У такой геометрической фигуры все грани представлены в виде плоских прямоугольных фигур.
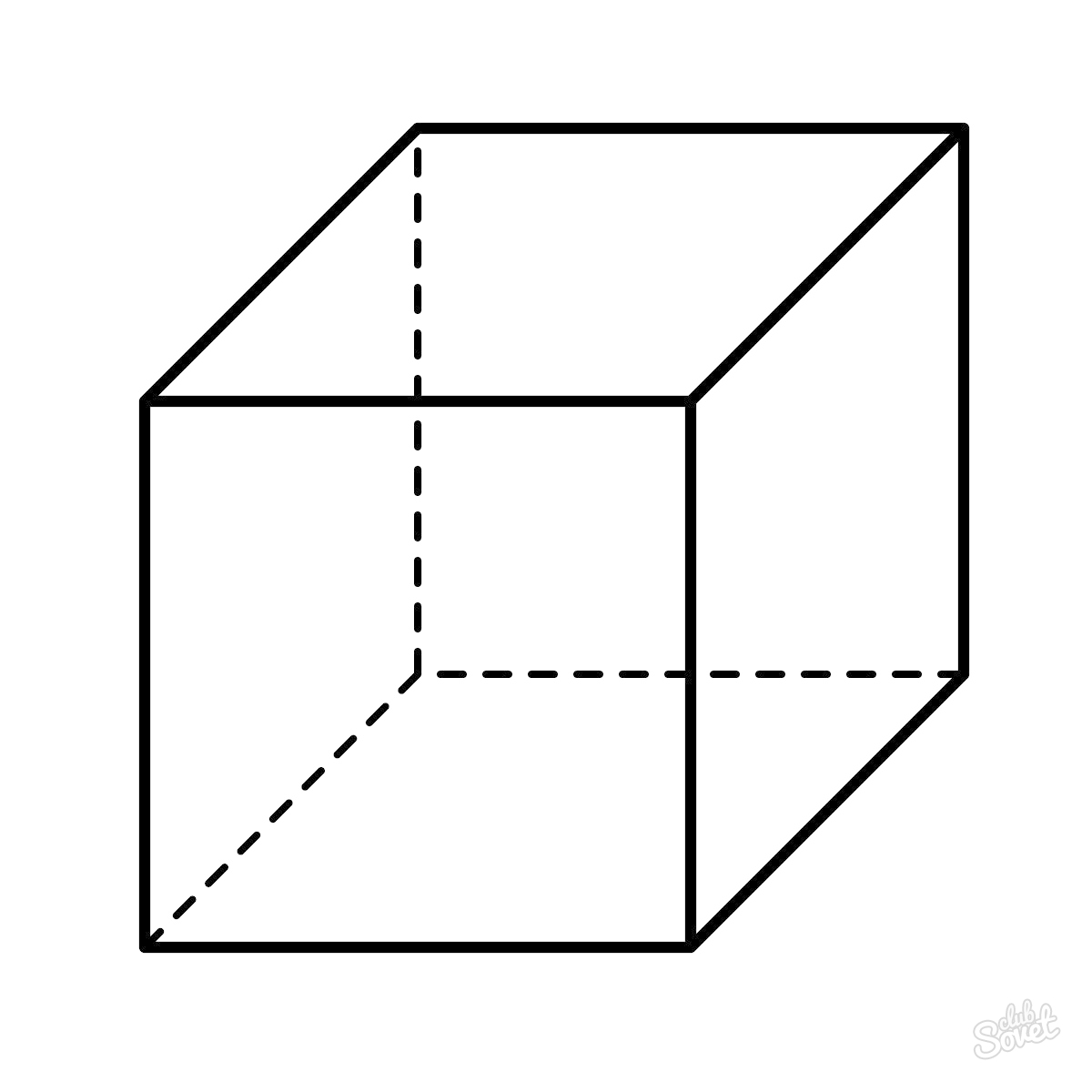
- Самый простой прямоугольный параллелепипед – это куб. Все ребра куба равны между собой. Всего у такого параллелепипеда 6 граней, то есть 6 одинаковых квадратов. Объем такой фигуры рассчитывается таким образом:
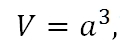
где a – длина любого ребра куба.
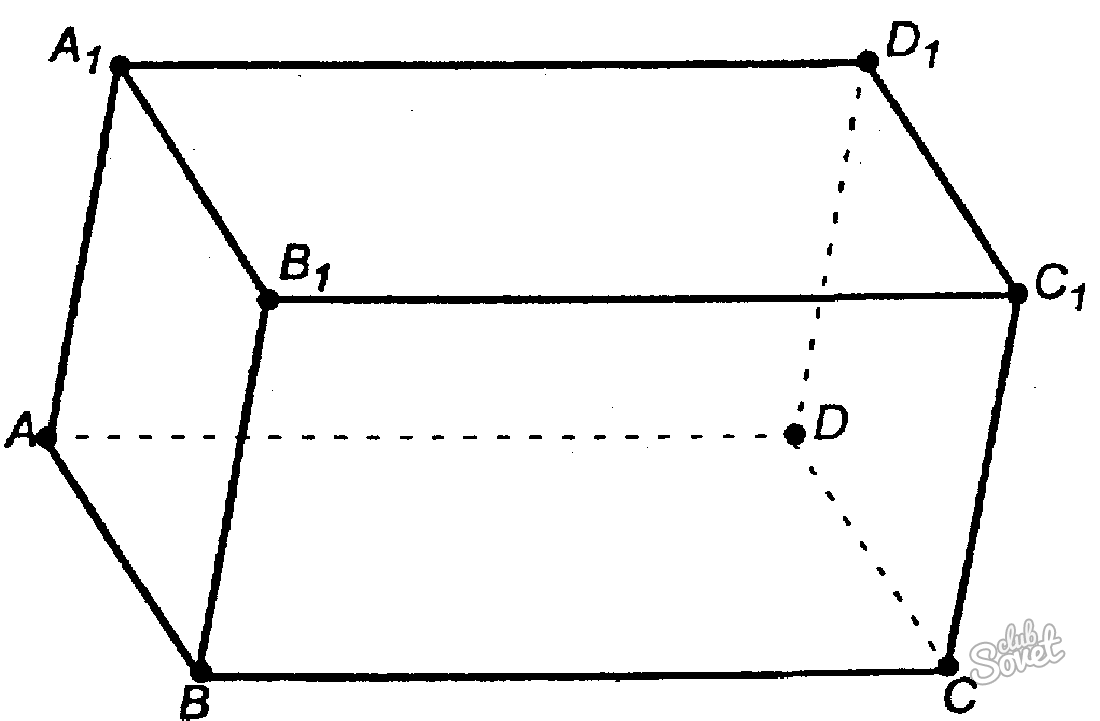
- Объем прямоугольного параллелепипеда, стороны которого имеют различные измерения, рассчитывается по следующей формуле:
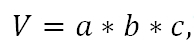
где a, b и с – длины ребер.
2
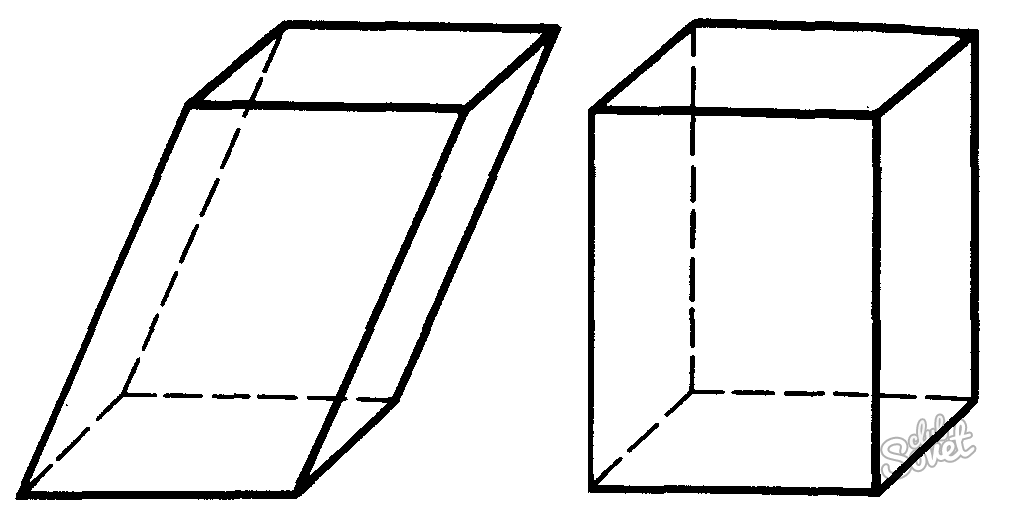
Как найти объем многогранника – наклонного параллелепипеда
У наклонного параллелепипеда так же 6 граней, 2 их них – основания фигуры, еще 4 – боковые грани. Наклонный параллелепипед отличается от прямого тем, что его боковые грани по отношению к основанию расположены не под прямым углом. Объем такой фигуры рассчитывается как произведение между площадью основания и высотой:
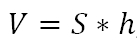
где S – это площадь четырехугольника, лежащего в основании, h – высота искомой фигуры.
3
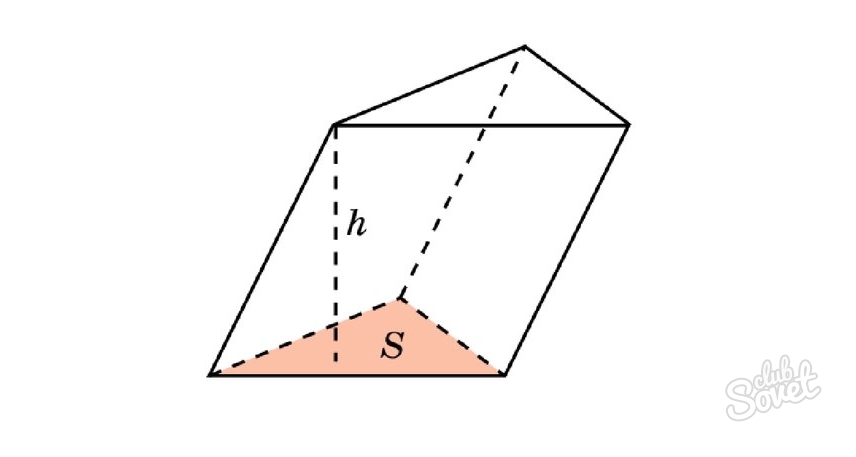
Как найти объем многогранника – призмы
Объемная геометрическая фигура, основание которой представлено многоугольником любой формы, а боковые грани – параллелограммами, имеющими общие стороны с основанием – называется призмой. У призмы два основания, а боковых граней столько, сколько сторон у фигуры, являющейся основанием.
Для нахождения объема любой призмы, как прямой, так и наклонной, умножают площадь основания на высоту:
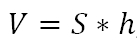
где S – площадь многоугольника в основании фигуры, а h – высота призмы.
4
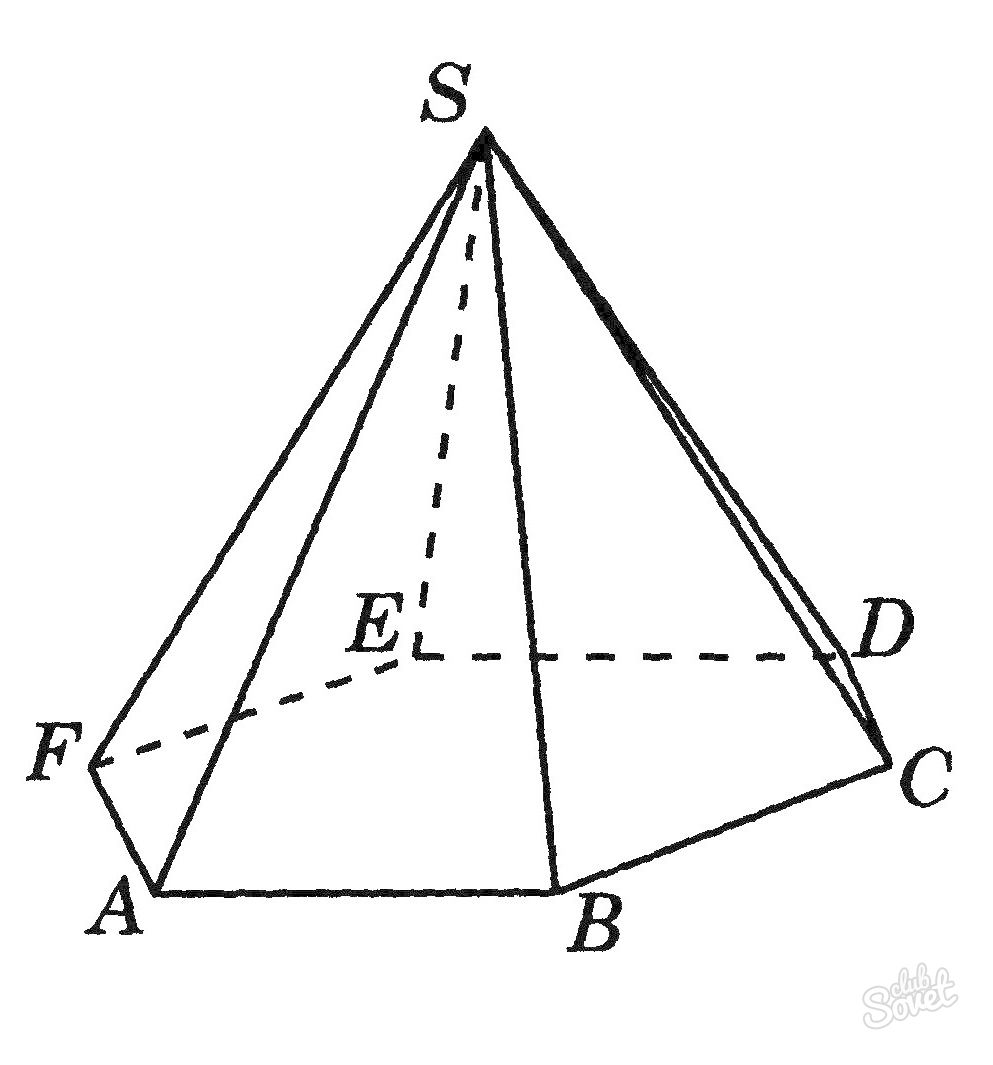
Как найти объем многогранника – пирамиды
Если в основании фигуры расположен многоугольник, а боковые грани представлены в виде треугольников, смыкающихся в общей вершине, то такую фигуру называют пирамидой. Она отличается от вышеперечисленных фигур тем, что у нее имеется только одно основание, кроме этого, у нее есть вершина. Чтобы найти объем пирамиды, ее основание умножают на высоту, и делят результат на 3:
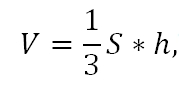
здесь S – площадь основания искомой геометрической фигуры, а h – высота.
Площадь простого многогранника найти достаточно просто, гораздо сложнее найти площадь фигуры, состоящей из множества многогранников. Особое внимание придется уделить правильному разделению сложного многогранника на простые.
Содержание материала
- Предварительный просмотр:
- Видео
- Понятие объема
- Как найти объем многогранника – наклонного параллелепипеда
- По теме: методические разработки, презентации и конспекты
- Методическое пособие к решению задач по дисциплине «Техническая механика»
- МЕТОДИЧЕСКИЕ УКАЗАНИЯ по решению контрольных заданий для обучающихся по заочной форме обучения по предмету «Элементы математической логики» Специальность: .. «Информационные системы»
- Методические указания и контрольные задания для студентов очной и заочной формы обучения по курсу: Основы электротехники, Электротехника и электронная техника для специльностей .. Электрификация и автоматизация с/х и .. Механизация с/х
- Тема. «Объёмы тел вращения». Методическое пособие по решению задач для студентов курса СПО. Дистанционная форма обучения.
Предварительный просмотр:
Тема. «Объёмы многогранников».
Методическое пособие по решению задач для студентов 2 курса СПО.
Дистанционная форма обучения.
1. Теоретический материал.
Вид многогранника
Формула объёма 1. Призма
V=S осн H 2. Прямоугольный параллелепипед
V=abc 3. Куб
V=a 3 4. Пирамида
V= S осн H 5.Усеченная пирамида
V= h
2. Решение задач.
Задача № 1
Найдите объем прямой призмы, в основании которой лежит ромб с диагоналями, равными 25 и 60, и боковым ребром, равным 25.
Дано:
АВСДА 1 В 1 С 1 Д 1 — прямая четырехугольная призма
АС = 60; ВД = 25; АА 1 = 25
Найти: V призмы
Решение
V призмы = S осн H; Н=АА 1
АВСД — ромб, следовательно S осн = ;
S осн = ; V призмы = 750 25=18750
Ответ. 18750
Задача № 2
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 8 и 15, боковое ребро равно 9. Найдите объем призмы.
Дано:
АВСА 1 В 1 С 1 — прямая треугольная призма.
АВС — прямоугольный; АС и ВС — катеты
АС = 15; ВС = 8; АА 1 = 9
Найти: V призмы
V призмы = S осн H; Н=АА 1
АВС — прямоугольный треугольник,
следовательно S осн = ;
S осн = ; V призмы = 60 9=540
Ответ. 540
Задача № 3.
В основании наклонной треугольной призмы лежит треугольник со сторонами 14; 12 и 12. Боковое ребро равно 6 и наклонено к плоскость основания под углом 30 . Найти объём призмы.
Дано:
АВСА 1 В 1 С 1 — наклонная треугольная призма.
АС = 12; ВС = 12; АВ = 14; СС 1 = 6; С 1 СО=30 .
Найти: V призмы
V призмы = S осн H;
ОСС 1 — прямоугольный треугольник, так как
С 1 О плоскости АВС; С 1 СО = 30 ;
С 1 О = С 1 С sin 30 = 6 = 3
Н=ОС 1 = 3
S осн = ; р= ;
р = ;
S осн =
V призмы =
Ответ. 21
Задача № 4.
Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба.
Дано: прямоугольный параллелепипед;
а=4; в=6; с=9. V п.п = V к
Найти : d
Решение:
V п.п =авс; V п.п = 4 6 9=216;
V к = d 3 ; d 3 = 216; d =
Ответ. 6
Задача № 5
От треугольной пирамиды, объем которой равен 34, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
Дано:
V SАВС = 34; SМN — сечение SАВС
MN — средняя линия треугольника АВС
Найти: V SMNC
Решение:
Так как MN — средняя линия треугольника АВС, то
MN = АВ , поэтому АВС подобен MNC.
Коэффициент подобия к=2, следовательно
; 2 2 ; 4;
Так как высоты пирамид SАВС и SMNC совпадают, то
V SMNC = V SАВС : 4= 34:4=8,5
Ответ. 8,5
Задача № 6
Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.
Дано: SABCD — пирамида; ABCD — прямоугольник;
АВ=3; ВС = 4; V SABCD = 16
Найти: H
Решение:
V= S осн H; V SABCD = S АВСD H;
S АВСD = АВ ВС; S АВСD = 3 4=12;
16= ; 4Н=16; Н=4
Ответ. 4
Задача № 7
Сторона основания правильной четырехугольной пирамиды равна 6 см, боковая грань наклонена к плоскости основания под углом 60°. Найти объем пирамиды.
Дано: SABCD — правильная четырехугольная пирамида;
АВ= 6 см ; SKO= 60°
Найти: V SABCD
Решение:
V SABCD = S осн H;
S осн = AB 2 ; S осн = (6 ) 2 = 36 3=108(см 2 )
SKO — прямоугольный треугольник, так как
SO — высота пирамиды;
SKO — линейный угол двугранного угла при основании пирамиды SABCD, следовательно
SKO = 60 ; ОК= АВ; ОК= 6 =3 (см)
; SO=OK tg60°=3 =9(cм);
Н=SО = 9см;
V SABCD = 108 9=324(см 3 )
Ответ. 324 см 3
Задача № 8
Основанием пирамиды является прямоугольник со сторонами 6см и 8см. Все боковые ребра равны 13 см. Найти объём пирамиды.
Дано: SABCD — пирамида; ABCD — прямоугольник;
АВ=6см; ВС = 8си; SA=SB=SC=SD=13cм.
Найти: V SABCD
Решение:
V SABCD = S осн H;
S АВСD = АВ ВС; S АВСD = 6 8=48(см 2 )
АВС — прямоугольный, по теореме Пифагора
АС 2 = АВ 2 + ВС 2 ; АС 2 = 6 2 + 8 2 =100; АС=10; AO=5см
SO АВСD, поэтому SАO прямоугольный, по теореме Пифагора
SO 2 = АS 2 — AO 2 ; SO 2 = 13 2 — 5 2 =169-25=144; SO=12см
Н=SO
V SABCD = 48 12=192(cм 3 )
Ответ. 192см 3
Задача № 9
Найдите высоту правильной треугольной пирамиды, стороны основания которой равны
2см, а объем равен см 3 .
Дано: SABC-правильная треугольная пирамида; АВ=2см;
V SABC = см 3
Найти: Н
Решение:
V SABC = S осн H;
АВС — правильный, поэтому S ABC = AB AC sin60 ;
S ABC = 2 2 sin60 =2 (см 2 );
= Н; Н= (см)
Ответ. 3
Задача № 10
Стороны оснований правильной четырехугольной усеченной пирамиды равны 3см и 5см. Найдите объем пирамиды, если ее боковое ребро равно 2 см и наклонено к плоскости основания под углом 60 градусов .
Дано: ABCDA 1 B 1 C 1 D 1 -правильная усеченная четырехугольная пирамида;
АВ=5см; A 1 B 1 = 3 см; DD 1 = 2 см; D 1 F (ABCD);
D 1 DF=60
Найти: V
Решение:
V= h
S 1 = ; S 2 = ; h = D 1 F
=АВ 2 ; = 5 2 = 25(см 2 )
=А 1 В 1 2 ; = 3 2 = 9(см 2 );
D 1 DF — прямоугольный, поэтому D 1 F= D 1 D sin60 ;
D 1 F = 2 sin60 = 2 (см);
V= (cм 3 )
Ответ. 49 см 3
Задания для самостоятельного решения
1. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна .
2. В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.
4 . Основанием прямой призмы является ромб со стороной 12см и углом 60º. Меньшее из диагональных сечений призмы является квадратом. Найти объем призмы.
5. В кубе AD 1 через середину ребер АВ, DС и вершину D 1 проведено сечение. Найдите объем куба, если площадь этого сечения равна .
Понятие объема
У людей давно возникла необходимость подсчитывать или отмерять необходимое количество разных веществ.

При измерении жидких и сыпучих материалов это было сделать легко, поместив их в сосуд известного объема. Для определения вместимости любых пространственных форм в стереометрии было введено понятие объема. Величина, описывающая размер части пространства, которую занимает геометрическое тело, называется его объемом и обозначается латинской буквой V. Для величины объема верны две аксиомы:
На величину объема никак не влияет ни пространственное местонахождение тела, ни то, каким образом оно делится на части. Как физическая величина объем выражается через массу и плотность вещества.
Чтобы понять, какая из емкостей более вместительная, можно заполнить одну жидкостью, а потом перелить в другую и увидеть, сколько жидкости останется или не хватит. Но это очень неудобно, и при решении геометрических задач пользуются понятием единицы измерения объема. Она равна объему куба, длина ребра которого — это единица длины.
Исторически известны разные меры емкостей — бушель, галлон, ведро, бочка и т. п. , объем нефти и сейчас измеряется в баррелях. В СИ за единицу объема принят 1 кубический метр, равный количеству вещества, вмещаемого кубом с длиной грани 1 м. В стереометрии обычно используются кубические сантиметры.
Видео
Как найти объем многогранника – наклонного параллелепипеда
У наклонного параллелепипеда так же 6 граней, 2 их них – основания фигуры, еще 4 – боковые грани. Наклонный параллелепипед отличается от прямого тем, что его боковые грани по отношению к основанию расположены не под прямым углом. Объем такой фигуры рассчитывается как произведение между площадью основания и высотой:


где S – это площадь четырехугольника, лежащего в основании, h – высота искомой фигуры.
По теме: методические разработки, презентации и конспекты

Методическое пособие к решению задач по дисциплине «Техническая механика»
Методическое пособие к решению задач предназначено для студентов строительных специальностей всех форм обучения, как вспомогательное пособие при выполнении ими самостоятельных работ и для …

МЕТОДИЧЕСКИЕ УКАЗАНИЯ по решению контрольных заданий для обучающихся по заочной форме обучения по предмету «Элементы математической логики» Специальность: .. «Информационные системы»
Методические указания по решению контрольных заданий для обучающихся по заочной форме обучения по предмету «Элементы математической логики», специальность 09.02.04 «Информационные системы»…

Методические указания и контрольные задания для студентов очной и заочной формы обучения по курсу: Основы электротехники, Электротехника и электронная техника для специльностей .. Электрификация и автоматизация с/х и .. Механизация с/х
АннотацияМетодические указания по дисциплине «Основы электротехники», «Электротехника и электронная техника» содержат четыре основных раздела курса. В каждом разделе даны краткая теория и примеры реше…

Тема. «Объёмы тел вращения». Методическое пособие по решению задач для студентов курса СПО. Дистанционная форма обучения
В данной методической разработке приведены формулы и разобраны примеры решения традиционных задач на вычисление объёмов тел вращения. Эта разработка предназначена для студентов СПО, находящихся на дис…

