Как найти обем многогранника

Многогранники

Многогранник – это поверхность, составленная из многоугольников, ограничивающая некоторое геометрическое тело.

В данной теме мы рассмотрим составные многогранники (многогранники, состоящие обычно из нескольких параллелепипедов).

Объемы различных многогранников:

• Призма $V=S_{осн}·h$
• Пирамида $V={1}/{3}S_{осн}·h$
• Параллелепипед $V=a·b·c$, где $a, b$ и $c$ – длина, ширина и высота.
• Куб $V=а^3$, где $а$ – сторона куба

Задачи на нахождение объема составного многогранника:

• Первый способ.

1. Составной многогранник надо достроить до полного параллелепипеда или куба.
2. Найти объем параллелепипеда.
3. Найти объем лишней части фигуры.
4. Вычесть из объема параллелепипеда объем лишней части.

• Второй способ

1. Разделить составной многогранник на несколько параллелепипедов.
2. Найти объем каждого параллелепипеда.
3. Сложить объемы.

Задачи на нахождение площади поверхности составного многогранника.

– Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:

$S_{полн.пов.}=P_{осн}·h+2S_{осн}$

Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.

– Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.

Задачи на нахождение расстояния между точками составного многогранника.

В данных задачах приведены составные многогранники, у которых двугранные углы прямые. Надо соединить расстояние между заданными точками и достроить его до прямоугольного треугольника. Далее остается воспользоваться теоремой Пифагора для нахождения нужной стороны.

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$АС^2+ВС^2=АВ^2$

Задачи на нахождение угла или значения одной из тригонометрических функций обозначенного в условии угла составного многогранника.

Так как в данных задачах приведены составные многогранники, у которых все двугранные углы прямые, то достроим угол до прямоугольного треугольника и найдем его значение по тригонометрическим значениям.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$:

Для острого угла $В: АС$ – противолежащий катет; $ВС$ – прилежащий катет.

Для острого угла $А: ВС$ – противолежащий катет; $АС$ – прилежащий катет.

1. Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	${1}/{2}$	${√2}/{2}$	${√3}/{2}$
$cosα$	${√3}/{2}$	${√2}/{2}$	${1}/{2}$
$tgα$	${√3}/{3}$	$1$	$√3$
$ctgα$	$√3$	$1$	${√3}/{3}$

Задачи на рассмотрение подобия фигур.

При увеличении всех линейных размеров многогранника в $k$ раз, площадь его поверхности увеличится в $k^2$ раз.

При увеличении всех линейных размеров многогранника в $k$ раз, его объём увеличится в $k^3$ раз.

Объемы геометрических тел

Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.

01 апреля 2019

Объемы геометрических тел

Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров «Российского учебника» учитель высшей категории Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.

Определение объема

Объем можно определить как функцию V на множестве многогранников, удовлетворяющую следующим аксиомам:

• V сохраняется при движениях.
• V удовлетворяет принципу Кавальери.
• Если внутренности многогранников M и N не пересекаются, то V(M ∪ N) = V(M) + V(N).
• Объем прямоугольного параллелепипеда V = abc.

Принцип Кавальери (итальянского математика, ученика Галилея). Если при пересечении двух тел плоскостями, параллельными одной и той же плоскости, в сечениях этих тел любой из плоскостей получаются фигуры, площади которых относятся как m : n, то объемы данных тел относятся как m : n.

В открытом банке заданий ЕГЭ есть много задач для отработки этого способа определения объема.

Примеры

Задача 1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.

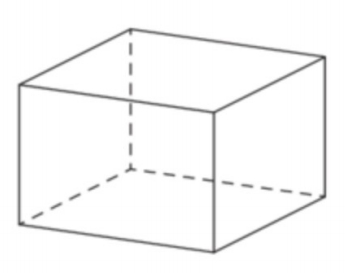
Задача 2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

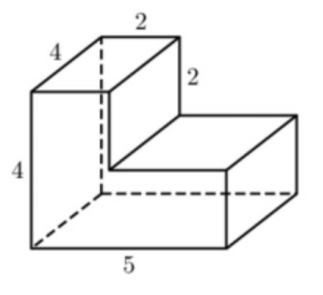
Задача 3. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

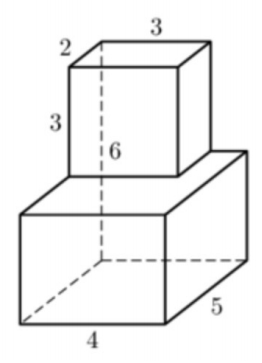
Разберем, как можно вычислять объемы изучаемых в школе фигур.

Объем призмы

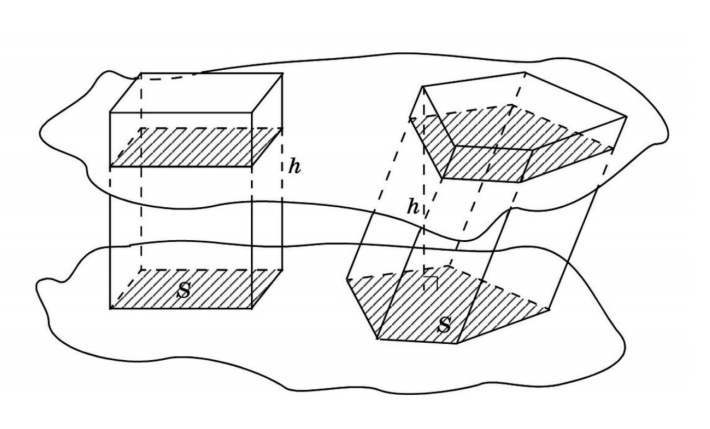
В представленном случае известны площадь основания и высота призмы. Чтобы найти объем, используем принцип Кавальери. Рядом с призмой (Ф₂) поместим прямоугольный параллелепипед (Ф₁), в основании которого — прямоугольник с такой же площадью, как у основания призмы. Высота у параллелепипеда такая же, как у наклонного ребра призмы. Обозначим третью плоскость (α) и рассмотрим сечение. В сечении виден прямоугольник с площадью S и, во втором случае, многоугольник тоже с площадью S. Далее вычисляем по формуле:

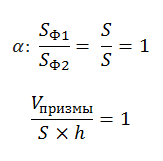
V S_осн h

Объем пирамиды

Лемма: две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики. Докажем это, используя принцип Кавальери.

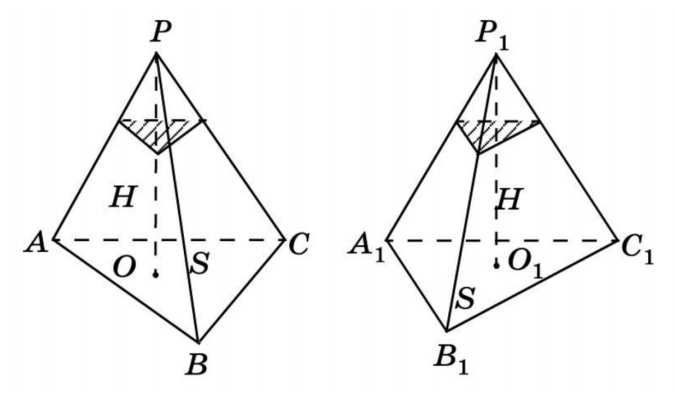
Возьмем две пирамиды одинаковой высоты и заключим их между двумя параллельными плоскостями α и β. Обозначим также секущую плоскость и треугольники в сечениях. Заметим, что отношения площадей этих треугольников связаны непосредственно с отношением оснований.

V ₁/V₂ = 1 <=> V₁ = V₂

Известно, что объем любой пирамиды равен одной трети произведения площади основания на высоту. Данной теоремой апеллируют довольно часто. Однако откуда в формуле объема пирамиды появляется коэффициент 1/3? Чтобы понять это, возьмем призму и разобьем ее на 3 треугольные пирамиды:

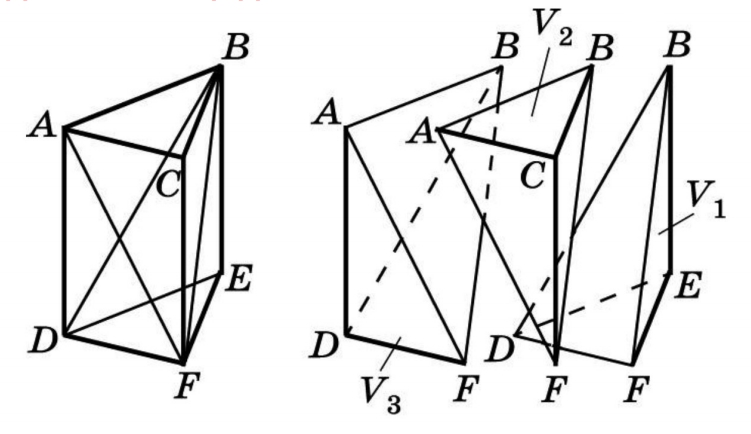
V₁ = V₂

V₂ = V₃

V_призмы S h = 3V

V = 1/3 Sh

Объем цилиндра

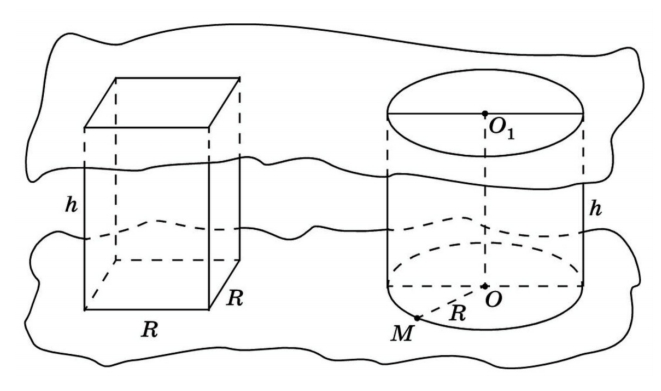
Возьмем прямой круговой цилиндр, в котором известны радиус основания и высота. Рядом поместим прямоугольный параллелепипед, в основании которого лежит квадрат. Рассмотрим:

V_цил = πh × R²

Объем конуса

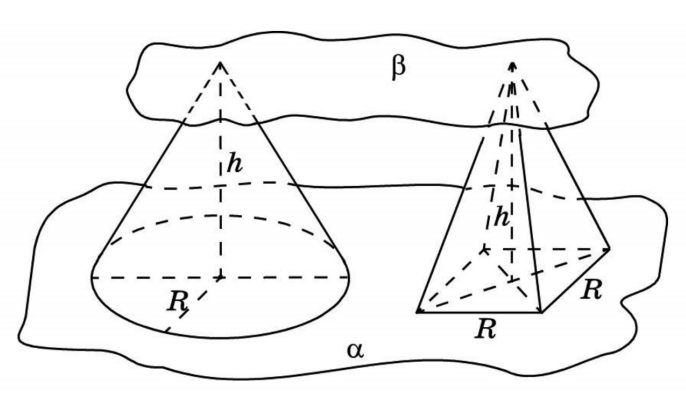
Конус лучше всего сравнивать с пирамидой. Например, с правильной четырехугольной пирамидой с квадратом в основании. Две фигуры с равными высотами заключаем в две параллельные плоскости. Обозначив третью плоскость, в сечении получаем круг и квадрат. Представления о подобиях приводят к числу π.

S_Ф1/S_Ф2 = π

V_конуса = 1/3 πR² h

Объем шара

Объем шара — одна из наиболее сложных тем. Если предыдущие фигуры можно продуктивно разобрать за один урок, то шар лучше отложить на последующее занятие.

Чтобы найти объем шара, шар часто предлагается сравнить со сложным геометрическим телом, которое связано с конусом и цилиндром. Но не стоит строить цилиндр, из которого вырезан конус, или вроде того. Возьмем половину шара с высотой R и радиусом R, а также конус и цилиндр с аналогичными высотами и радиусами оснований. Обратимся к полезным материалам на сайте
«Математические этюды», где объем шара рассматривается с использованием весов Архимеда. Цилиндр располагается на одной стороне уравновешенных весов, конус и половина шара — на другой.

Заключаем геометрические фигуры в две параллельные плоскости и смотрим, что получается в сечении. У цилиндра — круг с площадью πR². Как известно, если внутренности геометрических тел не пересекаются, то объем их объединения равен сумме объемов. Пусть в конусе и в половине шара расстояние до плоскости сечения будет x. Радиус — тоже x. Тогда площадь сечения конуса — π ∙ x². Расстояние от середины верха половины шара к краю сечения — R. Площадь сечения половины шара: π(R² — x²).

Заметим, что: πR² + πR² — πR² = πR²

V_цил = πR² × R = πR³ = 1/3 R³ π + V_шара

V_шара = 4/3 πR³

Итак, чтобы найти объем нового, не изученного геометрического тела, нужно сравнить его с тем телом, которое наиболее на него похоже. Многочисленные примеры заданий из открытого банка задач показывают, что в работе с фигурами имеет смысл использовать представленные формулы и аксиомы.

#ADVERTISING_INSERT#

Тема. «Объёмы многогранников».

Методическое пособие по решению задач для студентов 2 курса СПО.

Дистанционная форма обучения.

1. Теоретический материал.

Вид многогранника	Формула объёма
1. Призма	V=Sосн H
2. Прямоугольный  параллелепипед	V=abc
3. Куб	V=a3
4. Пирамида	V=Sосн H
5.Усеченная  пирамида	V=h

2. Решение задач.

Задача № 1

Найдите объем прямой призмы, в основании которой лежит ромб с диагоналями, равными 25 и 60, и боковым ребром, равным 25.

Дано:                                                                                                                                            АВСДА1В1С1Д1 – прямая четырехугольная призма  АС = 60; ВД = 25; АА1 = 25  Найти: V призмы  Решение V призмы = Sосн H;      Н=АА1 АВСД – ромб, следовательно     Sосн = ; Sосн = ;  V призмы = 75025=18750 Ответ.  18750

Задача № 2

Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 8 и 15, боковое ребро равно 9. Найдите объем призмы.

Дано: АВСА1В1С1 – прямая треугольная призма.  АВС – прямоугольный; АС и ВС – катеты АС = 15; ВС = 8;  АА1 = 9 Найти:   V призмы V призмы = Sосн H;      Н=АА1 АВС – прямоугольный треугольник, следовательно     Sосн = ; Sосн = ;  V призмы = 609=540 Ответ.  540

Задача №  3.

В основании наклонной треугольной призмы лежит треугольник со сторонами 14; 12 и 12. Боковое ребро равно 6 и наклонено к плоскость основания под углом 30. Найти объём призмы.

Дано: АВСА1В1С1 – наклонная треугольная призма. АС = 12; ВС = 12;  АВ = 14;  СС1 = 6; С1СО=30. Найти:   V призмы V призмы = Sосн H;       ОСС1 – прямоугольный треугольник, так как С1О  плоскости  АВС;    С1СО = 30; С1О = С1С sin 30= 6= 3 Н=ОС1 = 3 Sосн =  ; р=; р =; Sосн = V призмы = Ответ.  21

Задача №  4.

Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба. 

Дано: прямоугольный параллелепипед; а=4; в=6; с=9. Vп.п = Vк Найти : d Решение: Vп.п =авс; Vп.п = 469=216; Vк = d3;   d3 = 216;  d = Ответ. 6

Задача №  5

От треугольной пирамиды, объем которой равен 34, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

Дано: VSАВС = 34;   SМN – сечение SАВС MN – средняя линия треугольника АВС Найти: VSMNC Решение: Так как MN – средняя линия треугольника АВС, то MN = АВ , поэтому АВС подобен MNC. Коэффициент подобия к=2, следовательно ;     22;     4;   Так как высоты пирамид  SАВС и  SMNC совпадают, то VSMNC = VSАВС : 4= 34:4=8,5 Ответ. 8,5

Задача  № 6

 Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.

Дано: SABCD – пирамида; ABCD – прямоугольник; АВ=3; ВС = 4; VSABCD = 16 Найти: H Решение:  V=Sосн H;  VSABCD =  SАВСDH; SАВСD = АВВС; SАВСD = 34=12; 16=; 4Н=16;  Н=4 Ответ. 4

Задача №  7

Сторона основания правильной четырехугольной пирамиды равна 6см, боковая грань наклонена к плоскости основания под углом 60°. Найти объем пирамиды.

Дано: SABCD – правильная четырехугольная пирамида; АВ=6см; SKO=60° Найти: VSABCD Решение: VSABCD =Sосн H; Sосн = AB2;  Sосн = (6)2 = 363=108(см2) SKO – прямоугольный треугольник, так как SO – высота пирамиды;  SKO  – линейный угол двугранного угла при основании пирамиды SABCD, следовательно   SKO = 60;   ОК=АВ;   ОК=6=3(см) ;    SO=OKtg60°=3=9(cм); Н=SО = 9см; VSABCD =108 9=324(см3) Ответ. 324 см3

Задача №  8

Основанием пирамиды является прямоугольник со сторонами 6см и 8см. Все боковые ребра равны 13 см. Найти объём пирамиды.

Дано: SABCD – пирамида; ABCD – прямоугольник; АВ=6см; ВС = 8си; SA=SB=SC=SD=13cм. Найти: VSABCD Решение:  VSABCD =Sосн H;   SАВСD = АВВС; SАВСD = 68=48(см2) АВС – прямоугольный, по теореме Пифагора АС2 = АВ2 + ВС2 ;  АС2 = 62 + 82 =100; АС=10; AO=5см SO АВСD, поэтому SАO прямоугольный, по теореме Пифагора SO2 = АS2 – AO2 ;  SO2 = 132 – 52 =169-25=144; SO=12см Н=SO VSABCD =48 12=192(cм3) Ответ. 192см3

Задача №  9

Найдите высоту правильной треугольной пирамиды, стороны основания которой равны

2см, а объем равен  см3.

Дано: SABC-правильная треугольная пирамида; АВ=2см; VSABC = см3 Найти: Н Решение: VSABC =Sосн H; АВС – правильный, поэтому SABC = ABACsin600; SABC = 22sin600=2(см2); =Н;  Н=(см) Ответ. 3

Задача №  10

Стороны оснований правильной четырехугольной усеченной пирамиды равны 3см и 5см. Найдите объем пирамиды, если ее боковое ребро равно 2см и   наклонено к плоскости основания под углом 60 градусов​.

Дано: ABCDA1B1C1D1-правильная усеченная четырехугольная пирамида; АВ=5см; A1B1 = 3 см;  DD1 = 2см; D1F(ABCD);  D1DF=600 Найти: V Решение: V=h S1 =;         S2 =;     h = D1F =АВ2;      = 52 = 25(см2) =А1В12;  = 32 = 9(см2); D1DF – прямоугольный, поэтому  D1F= D1Dsin600; D1F = 2sin600=2(см); V=(cм3) Ответ. 49 см3

Задания для самостоятельного решения

1. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна .

2. В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.

3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.

4. Основанием прямой призмы является ромб со стороной 12см и углом 60º. Меньшее из диагональных сечений призмы является квадратом. Найти объем призмы.

5. В кубе AD1 через середину ребер АВ, DС и вершину D1 проведено сечение. Найдите объем куба, если площадь этого сечения равна .

Объём многогранника

Объёмы многогранников

Куб 

V = a3 , где а — ребро куба

Прямоугольный параллелепипед 

V = a * b * c, где a, b, c — рёбра фигуры: высота, ширина и длина

Параллелепипед

V = Sоснования * h, где  h — высота параллепипеда.

Призма

V = Sоснования * h, где  h — высота призмы

Пирамида

V = 1/3 Sоснования * h, где  h — высота пирамиды

Объёмы тел вращения

Цилиндр 

V = πR2h, где R — радиус основания, h — высота

Конус

V = 13 Sоснования * h

Шар

V = 43πR3 , где R — радиус шара