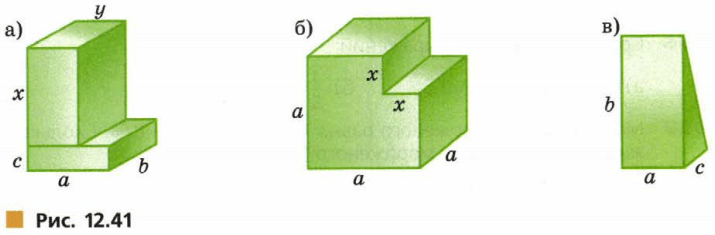
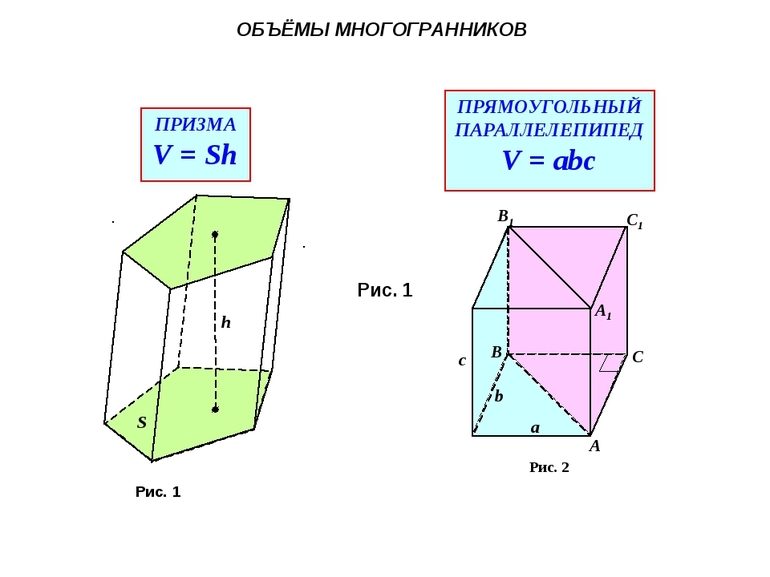
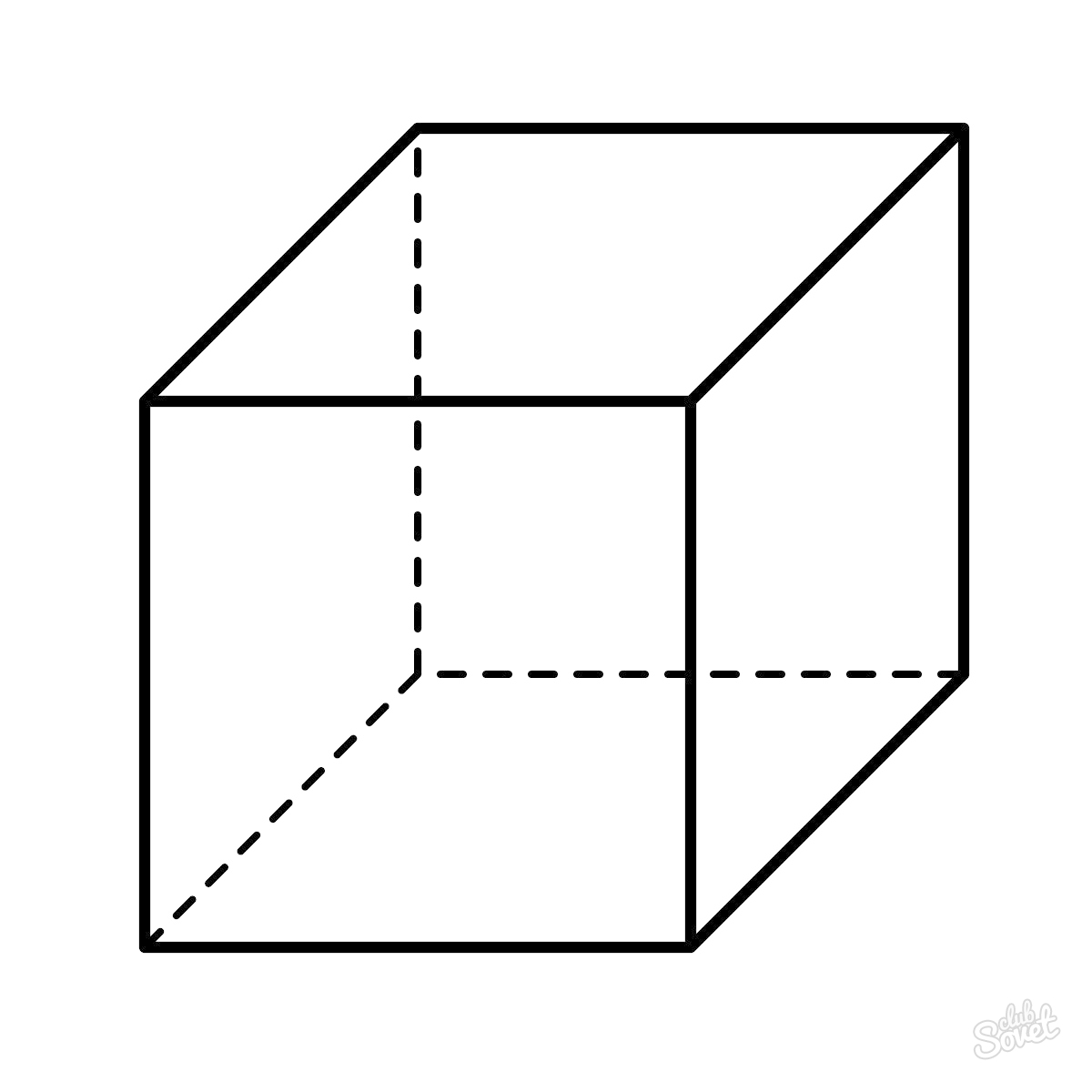
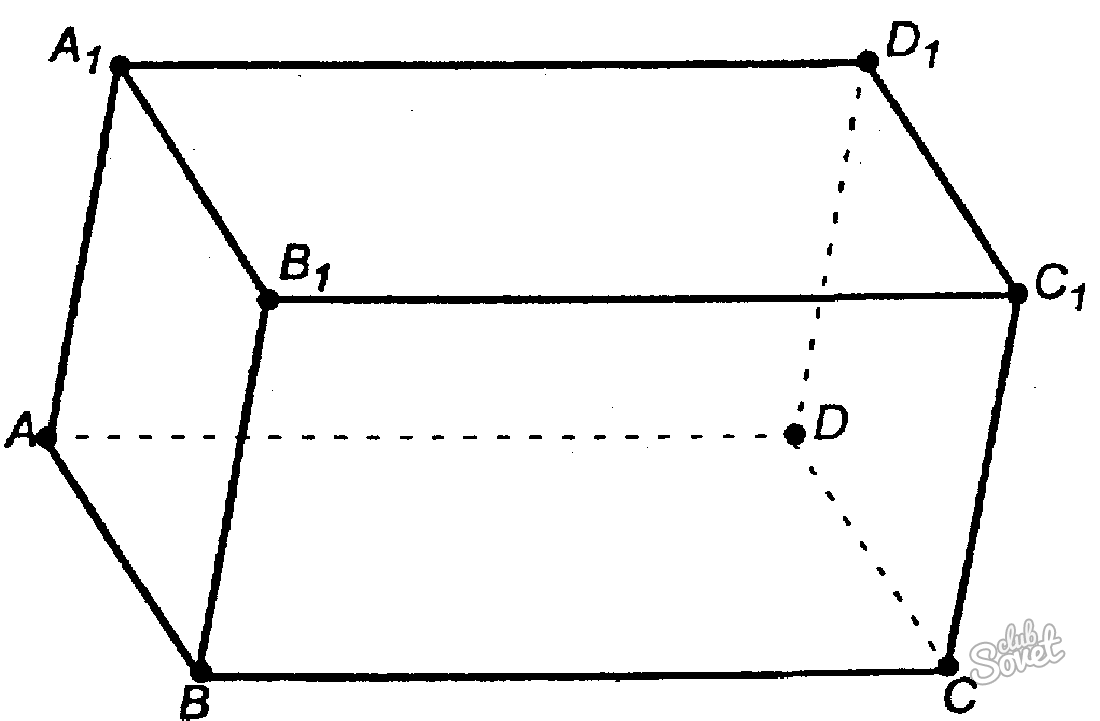
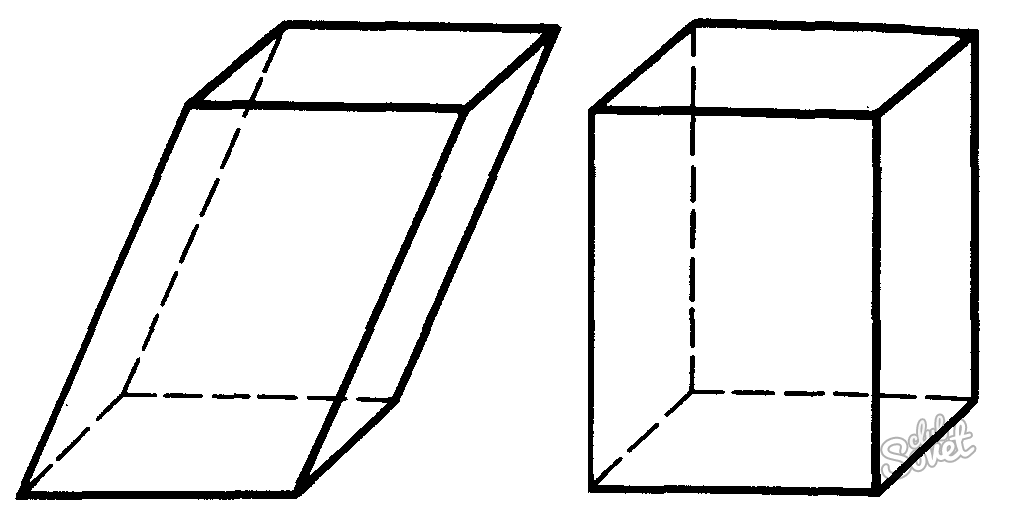
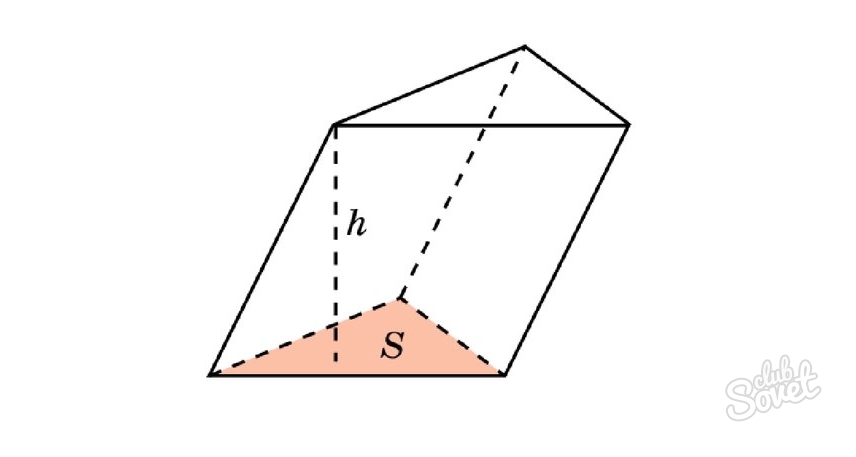
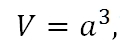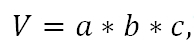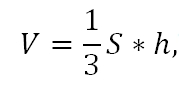Запишите формулу для вычисления объема V многогранника (рис.12.41,а−в).
reshalka.com
ГДЗ учебник по математике 6 класс Дорофеев. 12.3 Призма. Номер №1051
Решение а
1) x * y * b − объем верхней фигуры;
2) c * a * b − объем нижней фигуры;
3) x * y * b + c * a * b = b(xy + ac) − объем многогранника.
Ответ: V = b(xy + ac)
Решение б
1)
a
∗
a
∗
a
=
a
3
− объем куба;
2)
x
∗
x
∗
a
=
x
2
∗
a
− объем выпиленной части;
3)
a
3
−
x
2
∗
a
=
a
(
a
2
−
x
2
)
− объем многогранника.
Ответ:
V
=
a
(
a
2
−
x
2
)
Решение в
1) a * b * c − объем прямоугольного параллелепипеда;
2)
a
∗
b
∗
c
:
2
=
a
b
c
2
− объем многогранника.
Ответ:
V
=
a
b
c
2
В стереометрии изучаются свойства самых разнообразных объемных тел, в том числе приводятся доказательства формул объемов многогранников от самого простого — куба — до сложных геометрических тел с n-м количеством граней.
Определение геометрических тел
Один из разделов геометрии — стереометрия — изучает самые разнообразные пространственные фигуры и их свойства. В общем случае геометрическое тело — это часть пространства, имеющая наружные границы в виде замкнутой поверхности. Сугубо геометрическое определение описывает любую пространственную форму как компактную совокупность множества точек, каждые две из которых можно соединить отрезком и он будет полностью находиться внутри заданного ограниченного контура.
Совокупность всех точек, которые находятся на границе тела, составляет его поверхность. Кроме того, можно сказать, что любое геометрическое тело образовано множеством внутренних точек. В
иды пространственных фигур:
- многогранники;
- тела вращения.
Конечное число плоских многоугольников, ограничивающих пространственное тело, называется многогранником. При этом должны соблюдаться два свойства:
- Любая сторона каждого из многоугольников одновременно является стороной другого многоугольника и только их двоих. Соприкасающиеся стороны называются смежными.
- Все многоугольники связаны между собой — от каждого из них можно проложить путь до любого другого через смежные стороны.
В геометрии многоугольники, образующие сложный пространственный многогранник, называют гранями, отрезки, образованные местом соединения двух смежных граней — ребрами, а углы, образованные соединенными в одной точке гранями — вершинами.
Общий принцип названий таких геометрических тел заключается в указании количества их сторон.
Таким образом, если число граней обозначить n, то название образуется как n-гранник:
- 4 грани — четырехгранник;
- 5 граней — пятигранник;
- 6 граней — шестигранник;
- 8 граней — восьмигранник.
Если весь многогранник находится только с одной стороны каждой своей грани, то его называют выпуклым, в противном случае — вогнутым или невыпуклым. Звездчатые многогранники, состоящие из множества правильных пространственных фигур, относятся к невыпуклым.
Отрезок, проложенный между двумя вершинами, принадлежащими разным граням и соединяющий их — диагональ многогранника.
Понятие объема
У людей давно возникла необходимость подсчитывать или отмерять необходимое количество разных веществ.
При измерении жидких и сыпучих материалов это было сделать легко, поместив их в сосуд известного объема. Для определения вместимости любых пространственных форм в стереометрии было введено понятие объема. Величина, описывающая размер части пространства, которую занимает геометрическое тело, называется его объемом и обозначается латинской буквой V. Для величины объема верны две аксиомы:
- Полный объем любого многогранника равен сумме объемов всех его простых частей. Это свойство используется при вычислении объемов составных пространственных фигур.
- У равных тел и объемы равные, что доказывается принципом наложения, и при параллельном переносе их объем не изменяется.
На величину объема никак не влияет ни пространственное местонахождение тела, ни то, каким образом оно делится на части. Как физическая величина объем выражается через массу и плотность вещества.
Чтобы понять, какая из емкостей более вместительная, можно заполнить одну жидкостью, а потом перелить в другую и увидеть, сколько жидкости останется или не хватит. Но это очень неудобно, и при решении геометрических задач пользуются понятием единицы измерения объема. Она равна объему куба, длина ребра которого — это единица длины.
Исторически известны разные меры емкостей — бушель, галлон, ведро, бочка и т. п. , объем нефти и сейчас измеряется в баррелях. В СИ за единицу объема принят 1 кубический метр, равный количеству вещества, вмещаемого кубом с длиной грани 1 м. В стереометрии обычно используются кубические сантиметры.
Виды многогранников
Различают несколько условных классов пространственных фигур.
К обычным или классическим относятся параллелепипеды всех разновидностей, пирамиды и призмы. Правильными или Платоновыми телами называют отдельную группу из пяти многогранников, состоящих только из правильных многоугольников. Полуправильными или Архимедовыми телами называют усеченные Платоновы тела.
Отдельно рассматриваются сложные многогранники, такие как звездчатые, криволинейные или составленные из классических геометрических тел. Следует отметить, что одно и то же геометрическое тело может относиться к разным классам или являться частным случаем другого. Например, параллелепипед — частный случай призмы, а куб — правильный многогранник и частный случай параллелепипеда. Объем произвольных многогранников определяется как сумма объемов его простых частей.
Призма и параллелепипед
Такие многогранники всегда образованы двумя конгруэнтными основаниями, принадлежащими параллельным плоскостям, и n-м числом параллелограммов, являющихся их боковыми гранями. Если все ребра перпендикулярны основаниям призмы, то она называется прямой. У наклонной призмы величина углов между ребрами и основаниями отличается от 90º. Для правильной призмы обязательно выполнение условия — ее основание должно быть правильным многоугольником.
Высота — важная характеристика этого многогранника, она обозначается как h и в численном выражении представляет собой длину перпендикулярного отрезка между его основаниями. У прямой призмы высота равна длине ее ребра.
Формула для призмы: V = Sо·h, где Sо — площадь основания.
Параллелепипед является частным случаем призмы с основанием в виде четырехугольного многоугольника — параллелограмма. Тела такой формы тоже могут быть прямыми или наклонными и имеют две пары противоположных граней и четыре смежных. Если в основании параллелепипеда лежит прямоугольник, а его грани перпендикулярны основаниям, то он называется прямоугольным.
Формула объема многогранника прямоугольного параллелепипеда: V = a·b·c, где a и b — длина и ширина основания, а c — высота ребра.
К другой разновидности призм относится призматоид, если его изобразить на рисунке, то легко заметить, что грани такого тела — треугольники, одна сторона которых совпадает со стороной верхнего или нижнего основания, или трапеции, основания которых совпадают со сторонами оснований призматоида. Формула Симпсона: V = h/6 x (Sо + 4S + S1), где Sо и S1 — обозначения площадей оснований, а S — площадь параллельного и равноудаленного от оснований сечения.
Разновидности пирамиды
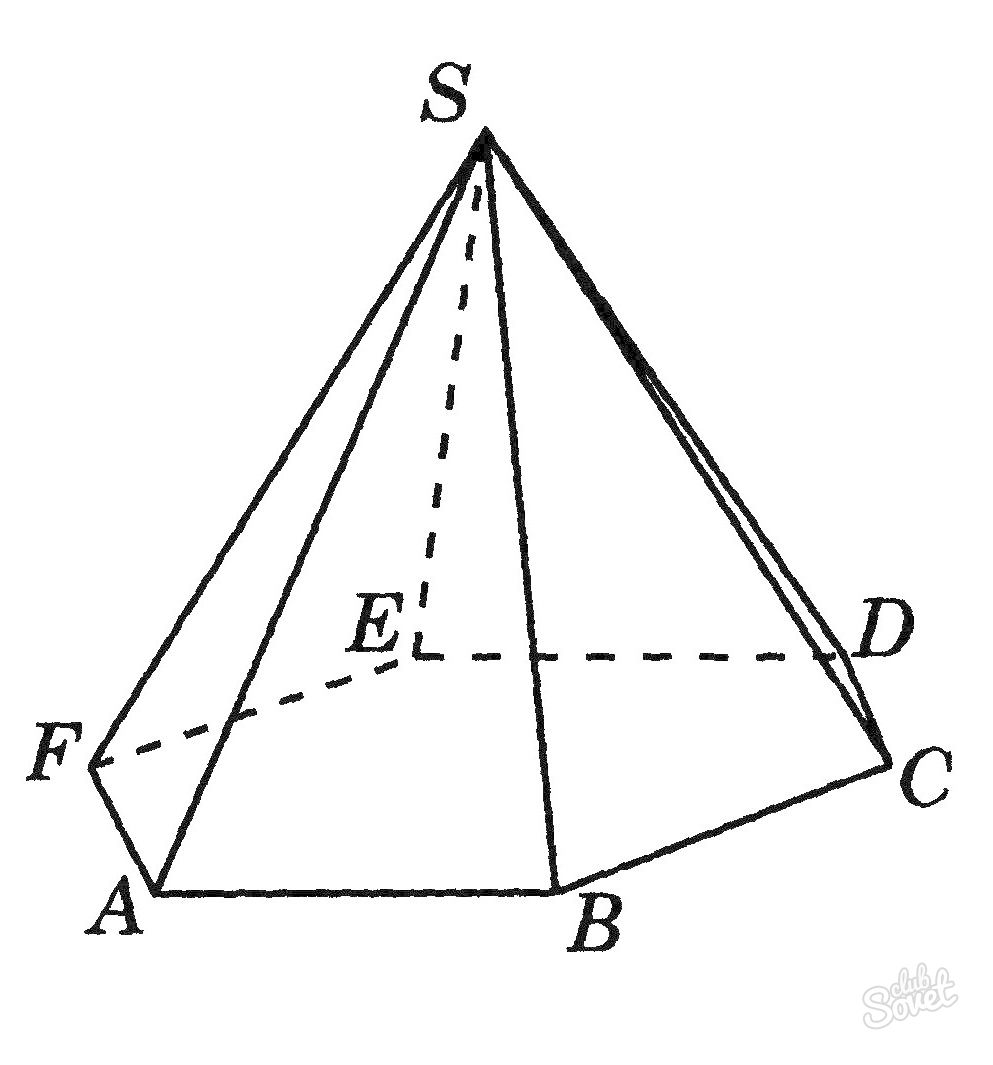
Пирамида представляет собой многогранник, строение которого включает в себя одно основание и n-е число треугольных граней, сходящихся в одной точке — вершине. К пирамидам относится простейший многогранник — четырехгранная пирамида, сторонами которой являются треугольники. В зависимости от того, какой многоугольник является основанием пирамиды, она может быть треугольной, четырехугольной, пятиугольной и т. д. Если при этом основания — правильные фигуры
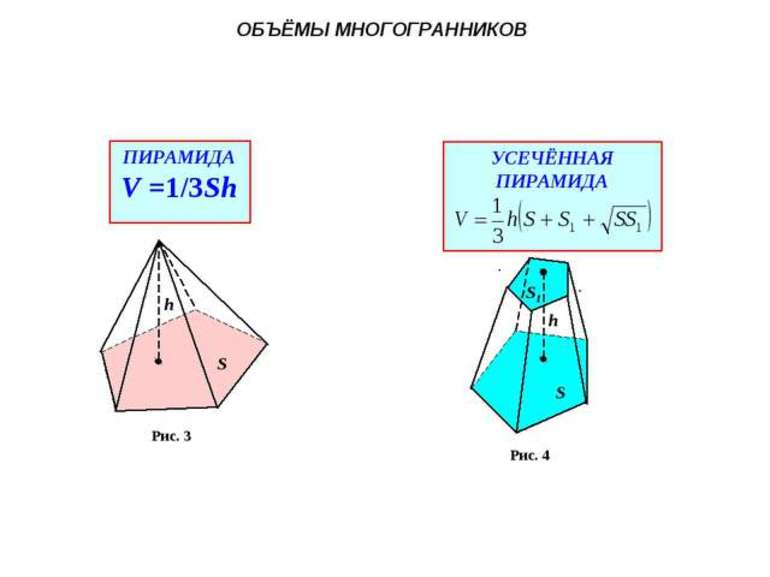
Формула расчета для пирамиды: V = 1/3 x So·h, где So — площадь основания, h — высота пирамиды, соединяющая ее вершину и центр основания.
Усеченная пирамида получается, если часть полной пирамиды отсекается параллельной основанию плоскостью. Получившееся сечение образует второе основание пирамиды.
Для усеченной пирамиды: V = 1/3 x h x (S1 + √(S1·S2) +S2), где S1 — площадь нижнего, а S2 — площадь верхнего оснований.
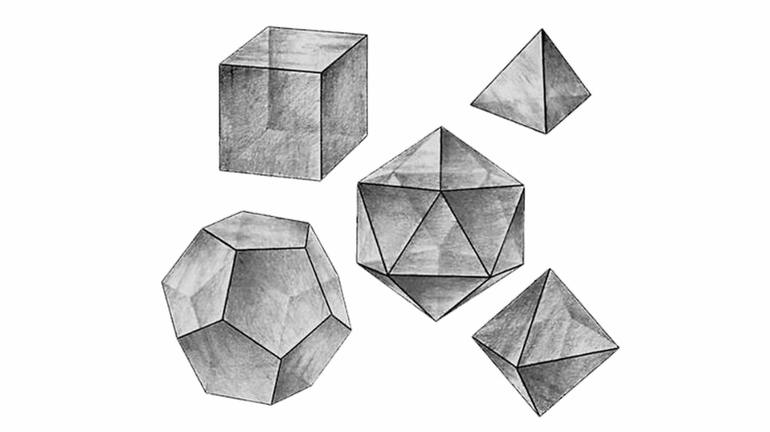
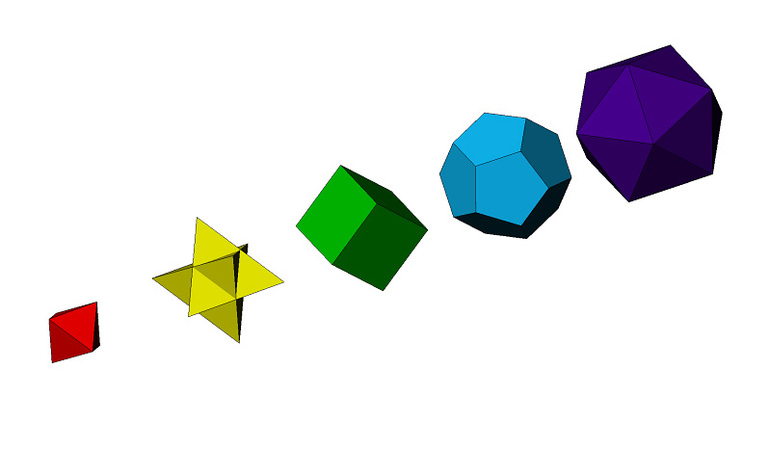
Правильные многогранники
Платоновы тела относятся к выпуклым многогранникам, обладают пространственной симметрией и состоят из одинаковых правильных многоугольников. Тетраэдр имеет форму пирамиды и состоит из четырех равносторонних треугольников. Его объем можно вычислить по стандартной формуле для пирамиды или так: V = √2/12 x a³, где a — длина ребра.
Следующий правильный многоугольник — это гексаэдр, который обычно называется кубом, у него шесть квадратных граней, следовательно, длины всех ребер равны между собой.
Формула объема куба: V = a³, где a — длина ребра.
Октаэдр имеет восемь треугольных граней. Формула объема этого правильного многогранника: V = (a³√2)/3.
Икосаэдр состоит из двадцати треугольных граней. Формула: V = (5a³(3 + √5))/12. Додекаэдр имеет 12 пятиугольных граней, а его объем вычисляется так: V = (a³(15 + 7√5))/4.
Тела вращения
Если какую-либо плоскую геометрическую фигуру вращать вокруг оси, расположенной в той же плоскости, то получится объемное тело вращения.
Шар образуется при вращении круга вокруг своей оси. Если сделать оборот прямоугольника вокруг одной из его сторон, то получится цилиндр. Конус образуется вращением треугольника по линии одного из его катетов. Окружность, вращающаяся вокруг прямой, ее не пересекающей, образует тор. Объемы сложных криволинейных тел определяются по специальной формуле с помощью интеграла.
Формулы для определения объема тел вращения приведены в таблице.
| Тело | Формула объема |
| Цилиндр | V = π R² h, R — радиус основания цилиндра, h — высота |
| Конус | V = 1/3 x π R² h, R — радиус основания конуса, h — высота |
| Шар | V = 4/3 x π R³, R — радиус, π — число пи, равное 3,14 |
Объемы деталей, представляющих собой составные многогранники можно вычислить с помощью онлайн-калькулятора.
Как найти объем многогранника
Прежде всего определимся, что же такое многогранник. Это трехмерная геометрическая фигура, грани которой представлены в виде плоских многоугольников. Единой формулы поиска объема многогранника не существует, так как многогранники бывают разной формы. Для того чтобы найти объем сложного многогранника, его условно делят на несколько простых, таких как параллелепипед, призма, пирамида, а затем складывают объемы простых многогранников и получают в результате искомый объем фигуры.
1
Как найти объем многогранника – параллелепипеда
Для начала найдем площадь прямоугольного параллелепипеда. У такой геометрической фигуры все грани представлены в виде плоских прямоугольных фигур.
- Самый простой прямоугольный параллелепипед – это куб. Все ребра куба равны между собой. Всего у такого параллелепипеда 6 граней, то есть 6 одинаковых квадратов. Объем такой фигуры рассчитывается таким образом:
где a – длина любого ребра куба.
- Объем прямоугольного параллелепипеда, стороны которого имеют различные измерения, рассчитывается по следующей формуле:
где a, b и с – длины ребер.
2
Как найти объем многогранника – наклонного параллелепипеда
У наклонного параллелепипеда так же 6 граней, 2 их них – основания фигуры, еще 4 – боковые грани. Наклонный параллелепипед отличается от прямого тем, что его боковые грани по отношению к основанию расположены не под прямым углом. Объем такой фигуры рассчитывается как произведение между площадью основания и высотой:
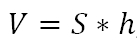
где S – это площадь четырехугольника, лежащего в основании, h – высота искомой фигуры.
3
Как найти объем многогранника – призмы
Объемная геометрическая фигура, основание которой представлено многоугольником любой формы, а боковые грани – параллелограммами, имеющими общие стороны с основанием – называется призмой. У призмы два основания, а боковых граней столько, сколько сторон у фигуры, являющейся основанием.
Для нахождения объема любой призмы, как прямой, так и наклонной, умножают площадь основания на высоту:
где S – площадь многоугольника в основании фигуры, а h – высота призмы.
4
Как найти объем многогранника – пирамиды
Если в основании фигуры расположен многоугольник, а боковые грани представлены в виде треугольников, смыкающихся в общей вершине, то такую фигуру называют пирамидой. Она отличается от вышеперечисленных фигур тем, что у нее имеется только одно основание, кроме этого, у нее есть вершина. Чтобы найти объем пирамиды, ее основание умножают на высоту, и делят результат на 3:
здесь S – площадь основания искомой геометрической фигуры, а h – высота.
Площадь простого многогранника найти достаточно просто, гораздо сложнее найти площадь фигуры, состоящей из множества многогранников. Особое внимание придется уделить правильному разделению сложного многогранника на простые.
Многогранник – это объемное тело, ограниченное замкнутой поверхностью, которая состоит из конечного числа многоугольников.
Содержание:
- Объемы многогранников
- Понятие объема фигур
- Принцип Кавальери
- Объем призмы
- Объем пирамиды
Понятие объема фигур
Объем — это величина, удовлетворяющая следующим основным свойствам:
1. Каждая фигура имеет определенный объем, выраженный положительным числом.
2. Равные фигуры имеют равные объемы.
3. Если фигура разбита на несколько частей, то ее объем равен сумме объемов всех этих частей.
4. Единицей измерения объема является объем куба с длиной ребра е, где е — единица измерения длины. Этот объем обозначается 
Если за единицу длины принимается 1 мм, то единицей объема является 


5. Объем куба со стороной 


где 
Мы будем говорить об объемах многогранников: кубе, прямоугольном параллелепипеде, призме, пирамиде и т. д.
Можно доказать теорему об объеме прямоугольного параллелепипеда:
Теорема 1. Объем прямоугольного параллелепипеда равен произведению трех его измерений.
где 
Из доказанной теоремы можно вывести следующее следствие.
Следствие. Любую грань прямоугольного параллелепипеда можно принять за основание; тогда сторонами его основания будут соответствующие два измерения, а высотой — третье измерение. Следовательно, объем прямоугольного параллелепипеда равен произведению площади его основания на высоту.
где S — площадь основания параллелепипеда, h — его высота.
Принцип Кавальери
Для вычисления объемов воспользуемся результатами, полученными итальянским математиком Бонавентура Кавальери (1598—1647), учеником Галилея, который сформулировал так называемый «принцип Кавальери» для вычисления объемов всех интересующих нас фигур. Поясним смысл этого принципа.
Представим себе физическую модель, очень похожую на четырехугольную пирамиду, сложенную из тонких (например, картонных) квадратиков последовательно убывающих размеров. На рисунке 2.511 изображена обычная пирамида, а на рис. 2.512 — приближенная ее модель из квадратных карточек.
Теперь допустим, что мы просверлили в предложенной модели узкое отверстие, ведущее от вершины к некоторой точке основания, и вставили в него стержень так, чтобы он пробивал каждую квадратную пластинку. Тогда можно, не меняя положения нижнего конца стержня на основании «пирамиды», наклонить стержень. Форма модели тогда изменится, но ее объем останется прежним. Дело в том, что объем нашей «пирамиды» — это просто общий объем всех квадратных пластинок, а этот общий объем не меняется, когда пластинки скользят одна по другой.
Сформулируем этот принцип в более общей ситуации.
Допустим, что мы имеем две фигуры, основания которых лежат в одной плоскости. Можно считать, что эта плоскость горизонтальна (рис. 2.513).
Если все горизонтальные поперечные сечения двух наших фигур, находящиеся на одном и том
же уровне, имеют одну и ту же площадь, то две наши фигуры имеют один и тот же объем.
Принцип Кавальери мы принимаем как основное свойство измерения объемов (можно это свойство считать аксиомой геометрии).
Пусть нам даны две фигуры 


Объем призмы
Определение. Поперечным сечением призмы называют пересечение призмы с плоскостью, параллельной плоскости ее основания.
Можно доказать теорему о свойствах поперечных сечений для случая треугольной призмы.
Теорема 2. Все поперечные сечения треугольной призмы равны ее основанию.
Это свойство верно для любых видов призм.
Имеет место теорема о свойстве площадей поперечных сечений призмы.
Теорема 3. Все поперечные сечения призмы имеют одну и ту же площадь.
Все выше сказанное позволяет доказать теорему об объеме призмы.
Теорема 4. Объем призмы равен произведению площади ее основания на высоту.
Итак,
где S — площадь основания призмы, a h — высота призмы.
Пример:
Найдите объем четырехугольной прямой призмы, высота которой равна h, диагонали наклонены к плоскости основания под углами 

Решение:
Из условия задачи имеем:
1. Четырехугольная призма 
2. Диагональ наклонена к плоскости основания под углом 
3. Острый угол между диагоналями основания равен
4. Найдите объем призмы 
Так как высота призмы дана, решение сводится к отысканию площади ее основания ABCD, которое является выпуклым четырехугольником.
Возникает самостоятельный вопрос: как найти площадь выпуклого четырехугольника? Известен такой факт:
площадь выпуклого четырехугольника выражается через его диагонали 


Следует также разобраться с данными п. 2.
5. 
6. 
7. Из треугольников 
8. Найдем площадь четырехугольника ABCD (рис. 2.515), диагонали которого АС и BD пересекаются в точке О.
9. 
Объем пирамиды
Горизонтальные поперечные сечения определяются для пирамиды так же, как и для призмы.
Определение. Поперечным сечением пирамиды называют ее пересечение с плоскостью, параллельной основанию.
На рисунке 2.516 



По мере того как горизонтальная плоскость движется от основания пирамиды к ее вершине, площадь поперечного сечения все время убывает, до тех пор, пока она не станет равной нулю.
В следующей теореме мы выведем формулу, показывающую, как изменяется площадь поперечного сечения для треугольной пирамиды:
Теорема 5. Каждое поперечное сечение треугольной пирамиды, заключенное между основанием и вершиной, является треугольником, подобным основанию. Если h — высота пирамиды и k — расстояние от вершины до плоскости поперечного сечения, то площадь поперечного сечения равна площади основания, умноженной на число 
Площади поперечных сечений ведут себя так: независимо от того, какую форму имеет основание пирамиды, отношение площадей всегда равно 
Теорема 6. Отношение площади поперечного сечения к площади основания пирамиды равно 
Приведенные выше теоремы позволяют нам доказать еще одну теорему.
Теорема 7. Если две пирамиды имеют одну и ту же площадь основания и одну и ту же высоту, то их поперечные сечения, равноудаленные от вершин, имеют одну и ту же площадь.
Имеет место одно из важнейших свойств пирамиды.
Теорема 8. Если две пирамиды имеют одну и ту же площадь основания и одну и ту же высоту, то они имеют один и тот же объем.
Можно также доказать теорему о нахождении объема треугольной пирамиды.
Теорема 9. Объем треугольной пирамиды равен одной трети произведения площади ее основания на высоту.
Тот же результат сохраняется и для любых пирамид.
Теорема 10. Объем пирамиды равен одной трети произведения площади ее основания на высоту.
Итак,
где S — площадь основания пирамиды, a h — высота пирамиды.
Теорема 11. Объем усеченной пирамиды с площадями оснований 
Пример:
Основание пирамиды — равнобедренный треугольник со сторонами 6 см, 6 см и 8 см. Все боковые ребра равны 9 см. Найдите объем пирамиды.
Решение:
Из условия задачи имеем:
1. РАВС — треугольная пирамида.
2. 
3. РА = РВ = PC = 9 см.
4. 
5. Итак, нахождение объема пирамиды сводится к нахождению площади основания — 
6. Проведем высоту пирамиды — РО = Н (построение) (рис. 2.518).
7. Так как боковые ребра пирамиды равны, основание О высоты пирамиды РО есть центр описанной около основания окружности (1,3, свойство пирамиды).
8. Основание высоты — точка О — принадлежит высоте равнобедренного треугольника ABC, проведенной к основанию АВ (6, 7, свойства пирамиды).
Нам будет удобно отдельно рассмотреть основание пирамиды — 
Возникает задача на плоскости: в равнобедренном треугольнике ABC АВ = б см, АС = б см, ВС = = 8 см. Найти ОБ — центр описанной около 
9. Соединим точку О с точкой Бис точкой М — серединой стороны АВ (построение) (рис. 2.519).
10. РО отыскивается по формуле 
Нам осталось найти радиус R.
Радиус R описанной около треугольника ABC окружности можно найти из треугольника АМО, где МО — серединный перпендикуляр к отрезку АВ. Это тоже отдельная задача на плоскости.
11. Обозначим угол МАО через 


12. 
13. 
14. Если D — середина ВС, то AD — высота основания. BD = CD = 

15. Площадь основания 
16. Объем пирамиды
Эта лекция взята со страницы полного курса лекций по изучению предмета “Математика”:
- Математика решение заданий и задач
Смотрите также дополнительные лекции по предмету “Математика”:
Лекции:
- Приложения определенного интеграла
- Дифференциальное вычисление функции одной переменной
- Решение слау
- Каноническое уравнение параболы
- Линейные (векторные) n – мерные пространства
- Решение задачи Коши
- Дифференциальные уравнения
- Алгебраические комплексные числа
- Рациональная функция
- Несобственный интеграл второго рода
Статьи
Среднее общее образование
Геометрия
Математика
Объемы геометрических тел
Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.
01 апреля 2019
Объемы геометрических тел
Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров «Российского учебника» учитель высшей категории Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.
Определение объема
Объем можно определить как функцию V на множестве многогранников, удовлетворяющую следующим аксиомам:
- V сохраняется при движениях.
- V удовлетворяет принципу Кавальери.
- Если внутренности многогранников M и N не пересекаются, то V(M ∪ N) = V(M) + V(N).
- Объем прямоугольного параллелепипеда V = abc.
Принцип Кавальери (итальянского математика, ученика Галилея). Если при пересечении двух тел плоскостями, параллельными одной и той же плоскости, в сечениях этих тел любой из плоскостей получаются фигуры, площади которых относятся как m : n, то объемы данных тел относятся как m : n.
В открытом банке заданий ЕГЭ есть много задач для отработки этого способа определения объема.
Примеры
Задача 1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
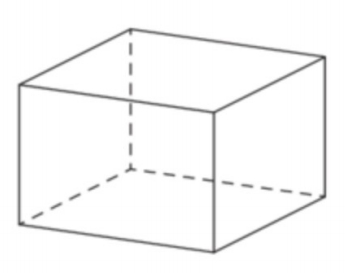
Задача 2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
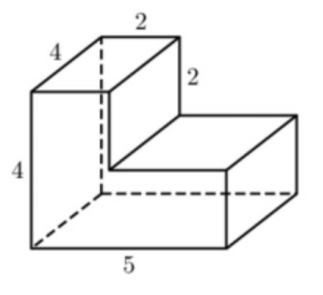
Задача 3. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
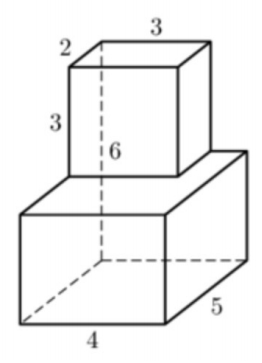
Разберем, как можно вычислять объемы изучаемых в школе фигур.
Объем призмы
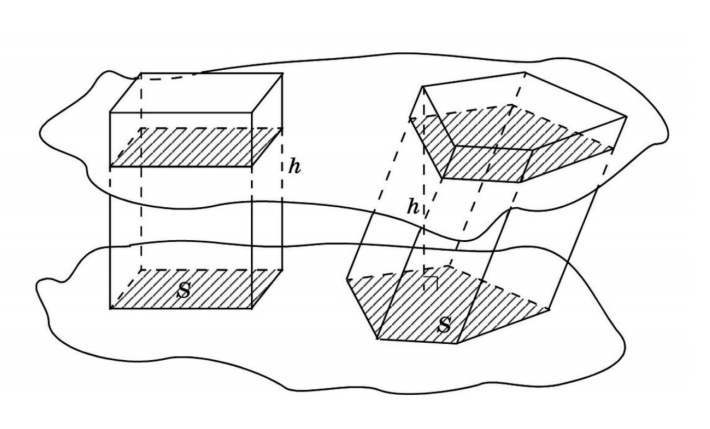
В представленном случае известны площадь основания и высота призмы. Чтобы найти объем, используем принцип Кавальери. Рядом с призмой (Ф2) поместим прямоугольный параллелепипед (Ф1), в основании которого — прямоугольник с такой же площадью, как у основания призмы. Высота у параллелепипеда такая же, как у наклонного ребра призмы. Обозначим третью плоскость (α) и рассмотрим сечение. В сечении виден прямоугольник с площадью S и, во втором случае, многоугольник тоже с площадью S. Далее вычисляем по формуле:
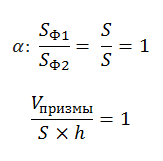
V Sосн h

Математика. Геометрия. Углублённый уровень. 11 класс. Задачник.
Задачник является Частью УМК для 10-11 классов, предназначенного для изучения предмета на углубленном уровне, и содержит более 1000 задач разной степени трудности, помогающих изучению и усвоению материала, изложенного в учебнике.
Пособие соответствует Федеральному государственному образовательному стандарту среднего (полного) общего образования.
Купить
Объем пирамиды
Лемма: две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики. Докажем это, используя принцип Кавальери.
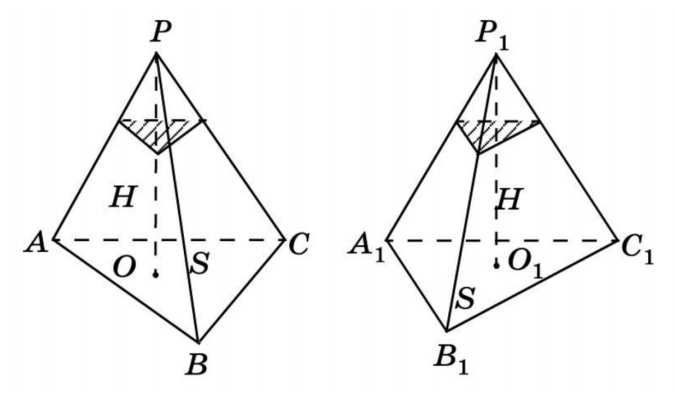
Возьмем две пирамиды одинаковой высоты и заключим их между двумя параллельными плоскостями α и β. Обозначим также секущую плоскость и треугольники в сечениях. Заметим, что отношения площадей этих треугольников связаны непосредственно с отношением оснований.

V 1/V2 = 1 <=> V1 = V2
Известно, что объем любой пирамиды равен одной трети произведения площади основания на высоту. Данной теоремой апеллируют довольно часто. Однако откуда в формуле объема пирамиды появляется коэффициент 1/3? Чтобы понять это, возьмем призму и разобьем ее на 3 треугольные пирамиды:
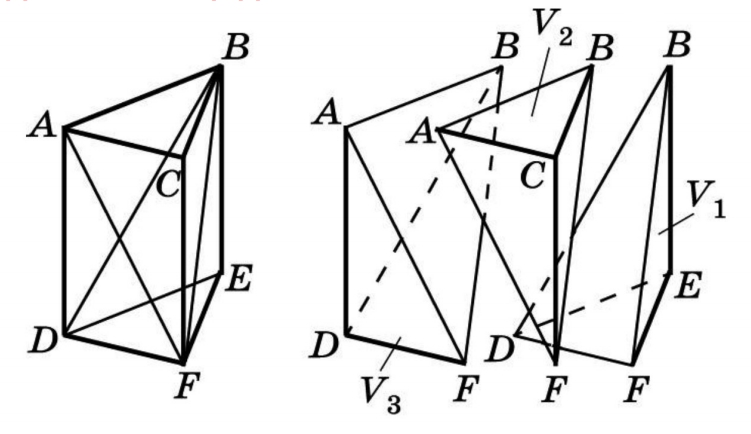
V1 = V2
V2 = V3
Vпризмы S h = 3V
V = 1/3 Sh
Объем цилиндра
Возьмем прямой круговой цилиндр, в котором известны радиус основания и высота. Рядом поместим прямоугольный параллелепипед, в основании которого лежит квадрат. Рассмотрим:

Vцил = πh × R2
Объем конуса
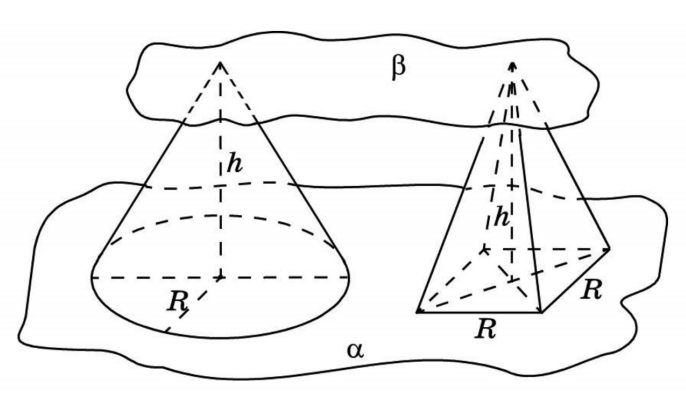
Конус лучше всего сравнивать с пирамидой. Например, с правильной четырехугольной пирамидой с квадратом в основании. Две фигуры с равными высотами заключаем в две параллельные плоскости. Обозначив третью плоскость, в сечении получаем круг и квадрат. Представления о подобиях приводят к числу π.
SФ1/SФ2 = π

Vконуса = 1/3 πR2 h
Объем шара
Объем шара — одна из наиболее сложных тем. Если предыдущие фигуры можно продуктивно разобрать за один урок, то шар лучше отложить на последующее занятие.
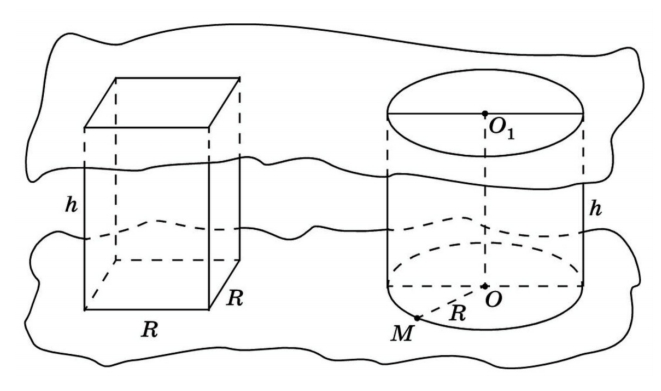
Чтобы найти объем шара, шар часто предлагается сравнить со сложным геометрическим телом, которое связано с конусом и цилиндром. Но не стоит строить цилиндр, из которого вырезан конус, или вроде того. Возьмем половину шара с высотой R и радиусом R, а также конус и цилиндр с аналогичными высотами и радиусами оснований. Обратимся к полезным материалам на сайте
«Математические этюды», где объем шара рассматривается с использованием весов Архимеда. Цилиндр располагается на одной стороне уравновешенных весов, конус и половина шара — на другой.
Заключаем геометрические фигуры в две параллельные плоскости и смотрим, что получается в сечении. У цилиндра — круг с площадью πR2. Как известно, если внутренности геометрических тел не пересекаются, то объем их объединения равен сумме объемов. Пусть в конусе и в половине шара расстояние до плоскости сечения будет x. Радиус — тоже x. Тогда площадь сечения конуса — π ∙ x2. Расстояние от середины верха половины шара к краю сечения — R. Площадь сечения половины шара: π(R2 — x2).
Заметим, что: πR2 + πR2 — πR2 = πR2
Vцил = πR2 × R = πR3 = 1/3 R3 π + Vшара
Vшара = 4/3 πR3
Итак, чтобы найти объем нового, не изученного геометрического тела, нужно сравнить его с тем телом, которое наиболее на него похоже. Многочисленные примеры заданий из открытого банка задач показывают, что в работе с фигурами имеет смысл использовать представленные формулы и аксиомы.
#ADVERTISING_INSERT#