Как найти объем многогранника решение

Как найти объем многогранника решение


СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика профильного уровня

Математика профильного уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Эксперту

Справочник

Карточки

Теория

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

1 мая

Новый сервис: можно исправить ошибки!

29 апреля

Разместили актуальные шкалы ЕГЭ  — 2023

24 апреля

Учителю: обновленный классный журнал

7 апреля

Новый сервис: ссылка, чтобы записаться к учителю

30 марта

Решения досрочных ЕГЭ по математике

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Каталог заданий.
Объем составного многогранника


Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

1

Тип 2 № 27044

i

Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

Аналоги к заданию № 27044: 4893 4903 4895 … Все

Решение

·

1 комментарий

·

Видеокурс

·

Помощь

2

Тип 2 № 27117

i

Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.

Решение

·

1 комментарий

·

Видеокурс

·

Помощь

3

Тип 2 № 27187

i

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Аналоги к заданию № 27187: 25531 25539 639857 … Все

Решение

·

Видеокурс

·

Помощь

4

Тип 2 № 27188

i

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Аналоги к заданию № 27188: 25551 25559 25553 … Все

Решение

·

Видеокурс

·

Помощь

5

Тип 2 № 27189

i

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Аналоги к заданию № 27189: 25571 25579 25573 … Все

Решение

·

Видеокурс

·

Помощь

Пройти тестирование по этим заданиям

О проекте · Редакция · Правовая информация · О рекламе

© Гущин Д. Д., 2011—2023

Источник

Многогранники

Многогранник – это поверхность, составленная из многоугольников, ограничивающая некоторое геометрическое тело.

В данной теме мы рассмотрим составные многогранники (многогранники, состоящие обычно из нескольких параллелепипедов).

Объемы различных многогранников:

  • Призма $V=S_{осн}·h$
  • Пирамида $V={1}/{3}S_{осн}·h$
  • Параллелепипед $V=a·b·c$, где $a, b$ и $c$ – длина, ширина и высота.
  • Куб $V=а^3$, где $а$ – сторона куба

Задачи на нахождение объема составного многогранника:

  • Первый способ.
  1. Составной многогранник надо достроить до полного параллелепипеда или куба.
  2. Найти объем параллелепипеда.
  3. Найти объем лишней части фигуры.
  4. Вычесть из объема параллелепипеда объем лишней части.

Пример:

Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).

Решение:

1. Достроим составной многогранник до параллелепипеда.

Найдем его объем. Для этого перемножим все три измерения параллелепипеда:

$V=10·9·4=360$

2. Найдем объем лишнего маленького параллелепипеда:

Его длина равна $9-4=5$

Ширина равна $4$

Высота равна $7$

$V=7·4·5=140$

3. Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:

$V=360-140=220$

Ответ: $220$

  • Второй способ
  1. Разделить составной многогранник на несколько параллелепипедов.
  2. Найти объем каждого параллелепипеда.
  3. Сложить объемы.

Задачи на нахождение площади поверхности составного многогранника.

– Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:

$S_{полн.пов.}=P_{осн}·h+2S_{осн}$

Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.

Пример:

Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).

Представим данный многогранник как прямую призму с высотой равной $12$.

$S_{полн.пов.}=P_{осн}·h+2S_{осн}$

$P_{осн}=8+6+6+2+2+4=28$

Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:

$S_1=6·6=36$

$S_2=2·4=8$

$S_осн=36+8=44$

Далее подставим все данные в формулу и найдем площадь поверхности многогранника

$S_{полн.пов.}=28·12+2·44=336+88=424$

Ответ: $424$

– Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.

Задачи на нахождение расстояния между точками составного многогранника.

В данных задачах приведены составные многогранники, у которых двугранные углы прямые. Надо соединить расстояние между заданными точками и достроить его до прямоугольного треугольника. Далее остается воспользоваться теоремой Пифагора для нахождения нужной стороны.

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$АС^2+ВС^2=АВ^2$

Задачи на нахождение угла или значения одной из тригонометрических функций обозначенного в условии угла составного многогранника.

Так как в данных задачах приведены составные многогранники, у которых все двугранные углы прямые, то достроим угол до прямоугольного треугольника и найдем его значение по тригонометрическим значениям.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$:

Для острого угла $В: АС$ – противолежащий катет; $ВС$ – прилежащий катет.

Для острого угла $А: ВС$ – противолежащий катет; $АС$ – прилежащий катет.

  1. Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
  2. Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
  3. Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

Значения тригонометрических функций некоторых углов:

$α$ $30$ $45$ $60$
$sinα$ ${1}/{2}$ ${√2}/{2}$ ${√3}/{2}$
$cosα$ ${√3}/{2}$ ${√2}/{2}$ ${1}/{2}$
$tgα$ ${√3}/{3}$ $1$ $√3$
$ctgα$ $√3$ $1$ ${√3}/{3}$

Задачи на рассмотрение подобия фигур.

При увеличении всех линейных размеров многогранника в $k$ раз, площадь его поверхности увеличится в $k^2$ раз.

При увеличении всех линейных размеров многогранника в $k$ раз, его объём увеличится в $k^3$ раз.

Источник

Тема. «Объёмы многогранников».

Методическое пособие по решению задач для студентов 2 курса СПО.

Дистанционная форма обучения.

1. Теоретический материал.

                    Вид многогранника

                   Формула объёма

                          1. Призма

               

V=Sосн H

     2. Прямоугольный  параллелепипед

   

V=abc

                                    3. Куб

 

V=a3

                                 4. Пирамида

         

V=Sосн H

                        5.Усеченная  пирамида

     

V=h

2. Решение задач.

Задача № 1

Найдите объем прямой призмы, в основании которой лежит ромб с диагоналями, равными 25 и 60, и боковым ребром, равным 25.

           

Дано:                                                                                                                                          

 АВСДА1В1С1Д1 – прямая четырехугольная призма

 АС = 60; ВД = 25; АА1 = 25

 Найти: V призмы 

Решение

V призмы = Sосн H;      Н=АА1

АВСД – ромб, следовательно     Sосн = ;

Sосн = ;  V призмы = 75025=18750

Ответ.  18750

Задача № 2

Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 8 и 15, боковое ребро равно 9. Найдите объем призмы.

Дано:

АВСА1В1С1 – прямая треугольная призма.

 АВС – прямоугольный; АС и ВС – катеты

АС = 15; ВС = 8;  АА1 = 9

Найти:   V призмы

V призмы = Sосн H;      Н=АА1

АВС – прямоугольный треугольник,

следовательно     Sосн = ;

Sосн = ;  V призмы = 609=540

Ответ.  540

Задача №  3.

В основании наклонной треугольной призмы лежит треугольник со сторонами 14; 12 и 12. Боковое ребро равно 6 и наклонено к плоскость основания под углом 30. Найти объём призмы.

Дано:

АВСА1В1С1 – наклонная треугольная призма.

АС = 12; ВС = 12;  АВ = 14;  СС1 = 6; С1СО=30.

Найти:   V призмы

V призмы = Sосн H;      

ОСС1 – прямоугольный треугольник, так как

С1О  плоскости  АВС;    С1СО = 30;

С1О = С1С sin 30= 6= 3

Н=ОС1 = 3

Sосн =  ; р=;

р =;

Sосн =

V призмы =

Ответ.  21

Задача №  4.

Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба. 

Дано: прямоугольный параллелепипед;

а=4; в=6; с=9. Vп.п = Vк

Найти : d

Решение:

Vп.п =авс; Vп.п = 469=216;

Vк = d3;   d3 = 216;  d =

Ответ. 6

Задача №  5

От треугольной пирамиды, объем которой равен 34, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

Дано:

VSАВС = 34;   SМN – сечение SАВС

MN – средняя линия треугольника АВС

Найти: VSMNC

Решение:

Так как MN – средняя линия треугольника АВС, то

MN = АВ , поэтому АВС подобен MNC.

Коэффициент подобия к=2, следовательно

;     22;     4;  

Так как высоты пирамид  SАВС и  SMNC совпадают, то

VSMNC = VSАВС : 4= 34:4=8,5

Ответ. 8,5

Задача  № 6

 Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.

Дано: SABCD – пирамида; ABCD – прямоугольник;

АВ=3; ВС = 4; VSABCD = 16

Найти: H

Решение:

 V=Sосн H;  VSABCD =  SАВСDH;

SАВСD = АВВС; SАВСD = 34=12;

16=; 4Н=16;  Н=4

Ответ. 4        

Задача №  7

Сторона основания правильной четырехугольной пирамиды равна 6см, боковая грань наклонена к плоскости основания под углом 60°. Найти объем пирамиды.

Дано: SABCD – правильная четырехугольная пирамида;

АВ=6см; SKO=60°

Найти: VSABCD

Решение:

VSABCD =Sосн H;

Sосн = AB2;  Sосн = (6)2 = 363=108(см2)

SKO – прямоугольный треугольник, так как

SO – высота пирамиды;

 SKO  – линейный угол двугранного угла при основании пирамиды SABCD, следовательно

  SKO = 60;   ОК=АВ;   ОК=6=3(см)

;    SO=OKtg60°=3=9(cм);

Н=SО = 9см;

VSABCD =108 9=324(см3)

Ответ. 324 см3

Задача №  8

Основанием пирамиды является прямоугольник со сторонами 6см и 8см. Все боковые ребра равны 13 см. Найти объём пирамиды.

Дано: SABCD – пирамида; ABCD – прямоугольник;

АВ=6см; ВС = 8си; SA=SB=SC=SD=13cм.

Найти: VSABCD

Решение:

 VSABCD =Sосн H;  

SАВСD = АВВС; SАВСD = 68=48(см2)

АВС – прямоугольный, по теореме Пифагора

АС2 = АВ2 + ВС2 ;  АС2 = 62 + 82 =100; АС=10; AO=5см

SO АВСD, поэтому SАO прямоугольный, по теореме Пифагора

SO2 = АS2 – AO2 ;  SO2 = 132 – 52 =169-25=144; SO=12см

Н=SO

VSABCD =48 12=192(cм3)

Ответ. 192см3

Задача №  9

Найдите высоту правильной треугольной пирамиды, стороны основания которой равны

2см, а объем равен  см3.

Дано: SABC-правильная треугольная пирамида; АВ=2см;

VSABC = см3

Найти: Н

Решение:

VSABC =Sосн H;

АВС – правильный, поэтому SABC = ABACsin600;

SABC = 22sin600=2(см2);

=Н;  Н=(см)

Ответ. 3

Задача №  10

Стороны оснований правильной четырехугольной усеченной пирамиды равны 3см и 5см. Найдите объем пирамиды, если ее боковое ребро равно 2см и   наклонено к плоскости основания под углом 60 градусов​.

Дано: ABCDA1B1C1D1-правильная усеченная четырехугольная пирамида;

АВ=5см; A1B1 = 3 см;  DD1 = 2см; D1F(ABCD);

 D1DF=600

Найти: V

Решение:

V=h

S1 =;         S2 =;     h = D1F

=АВ2;      = 52 = 25(см2)

=А1В12;  = 32 = 9(см2);

D1DF – прямоугольный, поэтому  D1F= D1Dsin600;

D1F = 2sin600=2(см);

V=(cм3)

Ответ. 49 см3

Задания для самостоятельного решения

1. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна .

2. В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.

3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.

4. Основанием прямой призмы является ромб со стороной 12см и углом 60º. Меньшее из диагональных сечений призмы является квадратом. Найти объем призмы.

5. В кубе AD1 через середину ребер АВ, DС и вершину D1 проведено сечение. Найдите объем куба, если площадь этого сечения равна .

Источник

Приветствую, сообщество Хакнем!

Сегодня в рубрике #хакнем_математика продолжим цикл статей, посвященных решению задач из ОГЭ и ЕГЭ по математике. Иногда в комментариях читатели спрашивают — зачем вы это пишите, и кому это нужно? Отвечаю — поверьте, кому-то это точно нужно! И даже, если моя статья поможет хоть 5-ти учащимся, я буду рада.

Иллюстрация защищена товарным знаком и принадлежит медиагруппе «Хакнем»
Иллюстрация защищена товарным знаком и принадлежит медиагруппе «Хакнем»

Недавно мой сын 11-классник пришёл ко мне с вопросом по задаче 8 (стереометрия) из ЕГЭ профильного уровня: «Ох, уж мне эта стереометрия, вроде решаю правильно, а ответ не сходится». Вот эта задача:

Задача 1

«Ох, уж мне эта стереометрия, вроде решаю правильно, а ответ не сходится»: задача 8 в ЕГЭ по математике. В чём подвох?

При решении этой задачи нам необходимо знать одну лишь формулу — формулу нахождения площади полной поверхности прямоугольного параллелепипеда с измерениями a, b, c: S = 2 ×(ab+ bc+ ac).

«Ох, уж мне эта стереометрия, вроде решаю правильно, а ответ не сходится»: задача 8 в ЕГЭ по математике. В чём подвох?

Как рассуждал сын? Он нашёл площадь нижнего параллелепипеда и площадь верхнего, и сложил результаты:

1. Площадь нижнего с измерениями 5×4×3 равна: S = 2 (5×4 + 4×3 + 5×3) = 94

2. Площадь верхнего с измерениями 3×2×3 равна: S = 2 (3×2 + 2×3 + 3×3) = 42

Если сложить эти два результата, получится 136. Где же ошибка?

Ошибка в том, что в найденных площадях и нижнего и верхнего параллелепипедов содержится площадь прямоугольника со сторонами 2×3 (S = 6, показана на рисунке красным, которая в площадь поверхности многогранника не входит.

«Ох, уж мне эта стереометрия, вроде решаю правильно, а ответ не сходится»: задача 8 в ЕГЭ по математике. В чём подвох?

Таким образом, из полученного результата надо вычесть две таких площади: 136 – 2×6 = 124. Ответ: 124.

Разберём ещё подобные задачи.

Задача 2

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые)
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые)

Решение:

Чтобы упростить решение задачи, достроим наш многогранник до параллелепипеда с измерениями 2×1×3.

Его площадь равна: S = 2 × (2×1 + 1×3 + 2×3) = 22.

«Ох, уж мне эта стереометрия, вроде решаю правильно, а ответ не сходится»: задача 8 в ЕГЭ по математике. В чём подвох?

Осталось вычесть площади «лишних» прямоугольников. Посмотрите на рисунок:

  • прямоугольник (его площадь), показанный розовой штриховкой, оставляем, так он входит в многогранник;
  • голубой тоже нужен;
  • а вот 2 зелёных (со сторонами 1 × 2) — лишние, их площади нужно вычесть.

Итак, S = 22 – 2 × (1×2) = 22 – 4 = 18.

Ответ: 18.

Задача 3

«Ох, уж мне эта стереометрия, вроде решаю правильно, а ответ не сходится»: задача 8 в ЕГЭ по математике. В чём подвох?

Решение:

А эту задачу решим немного другим способом. Если вы внимательно посмотрите на рис. в условии, то увидите, что это параллелепипед с вырезанным уголком (ну или с вдавленным). И если бы была такая возможность, и мы могли бы взять за уголок и потянуть, как показано стрелкой на рисунке, то параллелепипед станет «целым».

А это значит, чтобы найти искомую площадь поверхности многогранника нужно найти площадь поверхности прямоугольного параллелепипеда с измерениями 5×5×3:

S = 2 × (5×5 + 5×3 + 5×3) = 110.

Ответ: 110.

Задача 4

«Ох, уж мне эта стереометрия, вроде решаю правильно, а ответ не сходится»: задача 8 в ЕГЭ по математике. В чём подвох?

Решение:

Достроим снова для наглядности многогранник до прямоугольного параллелепипеда с измерениями 4×6×4. Его площадь:

S = 2×(4×6 + 6×4 + 4×4) = 128.

«Ох, уж мне эта стереометрия, вроде решаю правильно, а ответ не сходится»: задача 8 в ЕГЭ по математике. В чём подвох?
  • площадь жёлтого прямоугольника уже вошла в найденную площадь поверхности параллелепипеда;
  • 2 площади зелёных прямоугольников со сторонами 1×4 (S = 4) нужно добавить к найденной площади параллелепипеда;
  • 2 площади сиреневых прямоугольников со сторонами 1×2 (S = 2) — лишние, и поскольку они вошли в площадь параллелепипеда, а в искомом многограннике их на самом деле нет, то их вычтем.

Итак, S = 128 + 2×4 – 2×2 = 132.

Ответ: 132.

А в заключении приведу задачу с условием и рисунком, что и в задаче 1, но найти нужно объём многогранника.

Задача 5.

«Ох, уж мне эта стереометрия, вроде решаю правильно, а ответ не сходится»: задача 8 в ЕГЭ по математике. В чём подвох?

Решение:

Здесь всё намного проще. Достаточно найти объёмы 2-х параллелепипедов с измерениями 4×5×3 и 3×2×3 и сложить их.

Вспоминаем, что объём прямоугольного параллелепипеда с измерениями a, b, c находится по формуле: V = a×b×c.

V1 = 4 × 5 × 3 = 60;

V2 = 3 × 2 × 3 = 18;

V = 60 + 18 = 78.

Ответ: 78.

Не путайте на экзамене объём и площадь поверхности.

Вы всегда можете распечатать решение этих задач из Дзен или скопировать себе ссылку на статью, а при подготовке к экзамену ещё раз перечитать решение и вспомнить.

Удачи!

Кстати, принесла эти задачи своим коллегам на работу (не в школу, так как моя работа никак с ней не связана), так вот они с интересом эти задачки порешали. В ход пошли различные подручные “модели” и сложенные фигурки из бумаги. Ведь самое сложное в них — понять что лишнее, а что уже входит. Хорошая гимнастика ума!

Источник фото: proobraz27.ru
Источник фото: proobraz27.ru

Если нашли ошибку или опечатку, пишите в комментариях, буду благодарна.

#хакнем_математика (👈 подпишись на этот хэштег, чтобы получать новый интересный и познавательный контент по математике 🥳

Автор: #ирина_чудневцева координатор канала Хакнем Школа, 42 года, город Ярославль

Похожие статьи автора:

«Ох, уж мне эта стереометрия, вроде решаю правильно, а ответ не сходится»: задача 8 в ЕГЭ по математике. В чём подвох?

Если у вас есть познавательный материал, тёплые воспоминания и интересные истории из школьной жизни, которые вы хотели бы опубликовать в нашем канале, или вы просто хотите стать автором канала, напишите нам об этом 👉 story@haknem.com

«Ох, уж мне эта стереометрия, вроде решаю правильно, а ответ не сходится»: задача 8 в ЕГЭ по математике. В чём подвох?
Источник

Статьи

Среднее общее образование

Геометрия

Математика

Объемы геометрических тел


Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.

01 апреля 2019

Объемы геометрических тел

Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров «Российского учебника» учитель высшей категории Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.

Определение объема

Объем можно определить как функцию V на множестве многогранников, удовлетворяющую следующим аксиомам:

  • V сохраняется при движениях.
  • V удовлетворяет принципу Кавальери.
  • Если внутренности многогранников M и N не пересекаются, то V(M ∪ N) = V(M) + V(N).
  • Объем прямоугольного параллелепипеда V = abc.

Принцип Кавальери (итальянского математика, ученика Галилея). Если при пересечении двух тел плоскостями, параллельными одной и той же плоскости, в сечениях этих тел любой из плоскостей получаются фигуры, площади которых относятся как m : n, то объемы данных тел относятся как m : n.

В открытом банке заданий ЕГЭ есть много задач для отработки этого способа определения объема.

Примеры

Задача 1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.

Рисунок 1

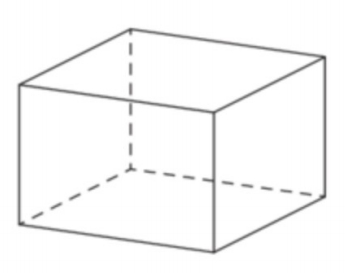
Задача 2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Рисунок 2

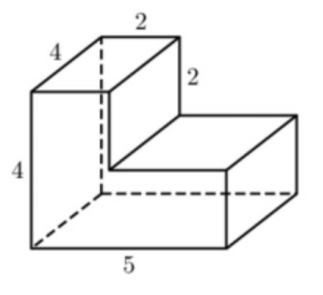
Задача 3. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Рисунок 3

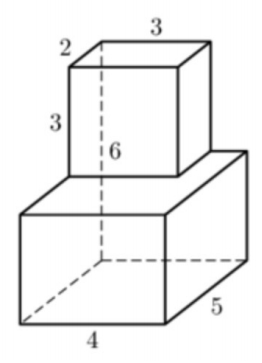
Разберем, как можно вычислять объемы изучаемых в школе фигур.

Объем призмы

Рисунок 4

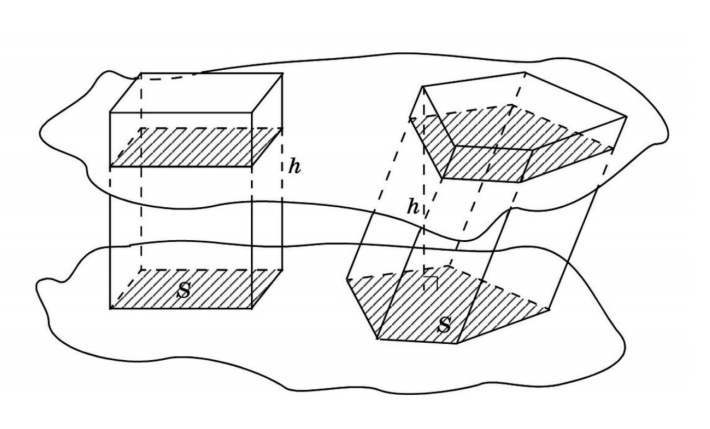
В представленном случае известны площадь основания и высота призмы. Чтобы найти объем, используем принцип Кавальери. Рядом с призмой (Ф2) поместим прямоугольный параллелепипед (Ф1), в основании которого — прямоугольник с такой же площадью, как у основания призмы. Высота у параллелепипеда такая же, как у наклонного ребра призмы. Обозначим третью плоскость (α) и рассмотрим сечение. В сечении виден прямоугольник с площадью S и, во втором случае, многоугольник тоже с площадью S. Далее вычисляем по формуле:

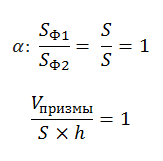
V Sосн h

Математика. Геометрия. Углублённый уровень. 11 класс. Задачник.

Математика. Геометрия. Углублённый уровень. 11 класс. Задачник.

Задачник является Частью УМК для 10-11 классов, предназначенного для изучения предмета на углубленном уровне, и содержит более 1000 задач разной степени трудности, помогающих изучению и усвоению материала, изложенного в учебнике.
Пособие соответствует Федеральному государственному образовательному стандарту среднего (полного) общего образования.

Купить

Объем пирамиды

Лемма: две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики. Докажем это, используя принцип Кавальери.

Рисунок 5

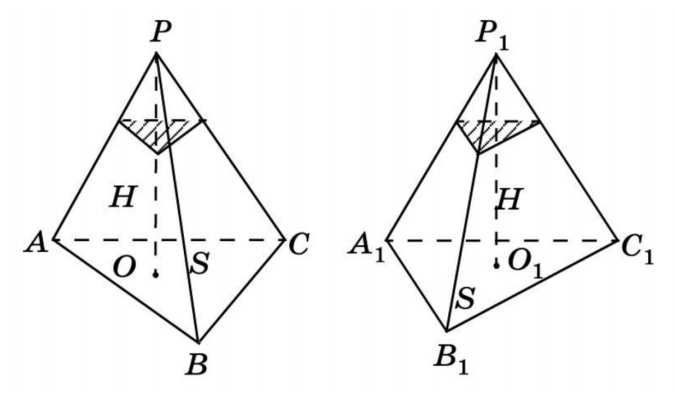
Возьмем две пирамиды одинаковой высоты и заключим их между двумя параллельными плоскостями α и β. Обозначим также секущую плоскость и треугольники в сечениях. Заметим, что отношения площадей этих треугольников связаны непосредственно с отношением оснований.

V 1/V2 = 1 <=> V1 = V2

Известно, что объем любой пирамиды равен одной трети произведения площади основания на высоту. Данной теоремой апеллируют довольно часто. Однако откуда в формуле объема пирамиды появляется коэффициент 1/3? Чтобы понять это, возьмем призму и разобьем ее на 3 треугольные пирамиды:

Рисунок 6

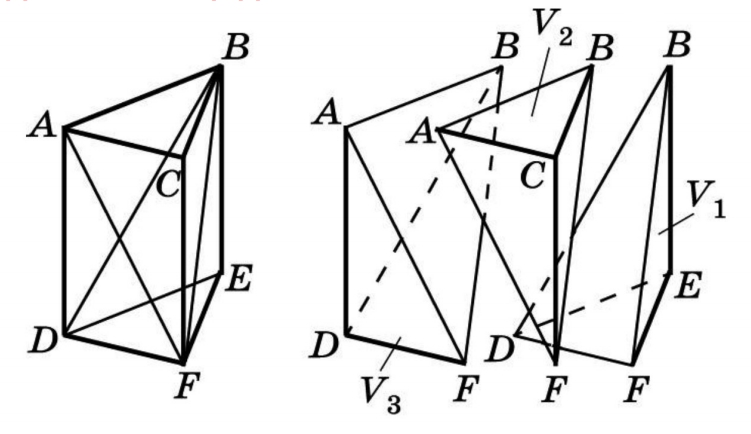
V1 = V2


V2 = V3


Vпризмы S h = 3V


V = 1/3 Sh

Объем цилиндра

Рисунок 7

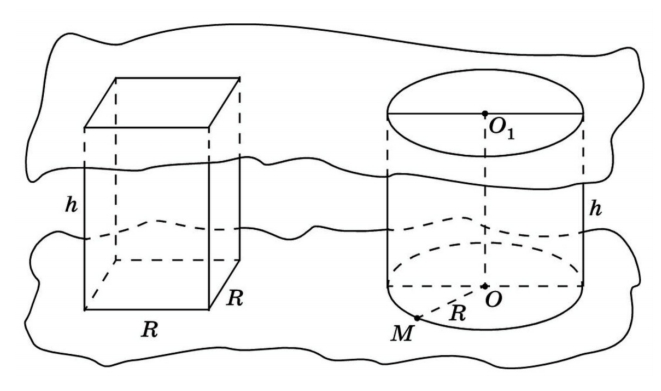
Возьмем прямой круговой цилиндр, в котором известны радиус основания и высота. Рядом поместим прямоугольный параллелепипед, в основании которого лежит квадрат. Рассмотрим:

Vцил = πh × R2

Объем конуса

Рисунок 8

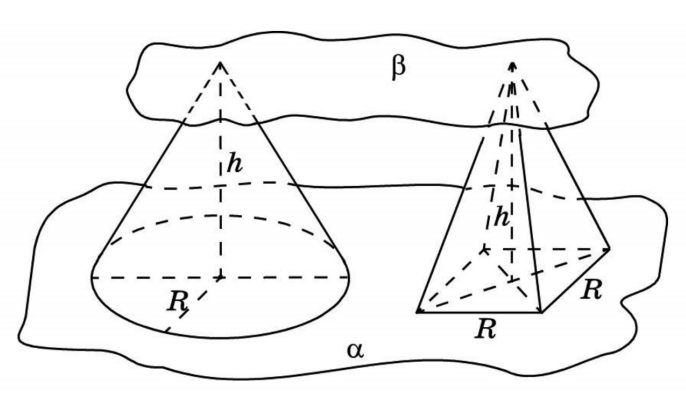
Конус лучше всего сравнивать с пирамидой. Например, с правильной четырехугольной пирамидой с квадратом в основании. Две фигуры с равными высотами заключаем в две параллельные плоскости. Обозначив третью плоскость, в сечении получаем круг и квадрат. Представления о подобиях приводят к числу π.

SФ1/SФ2 = π


Vконуса = 1/3 πR2 h

Объем шара

Объем шара — одна из наиболее сложных тем. Если предыдущие фигуры можно продуктивно разобрать за один урок, то шар лучше отложить на последующее занятие.

Чтобы найти объем шара, шар часто предлагается сравнить со сложным геометрическим телом, которое связано с конусом и цилиндром. Но не стоит строить цилиндр, из которого вырезан конус, или вроде того. Возьмем половину шара с высотой R и радиусом R, а также конус и цилиндр с аналогичными высотами и радиусами оснований. Обратимся к полезным материалам на сайте
«Математические этюды», где объем шара рассматривается с использованием весов Архимеда. Цилиндр располагается на одной стороне уравновешенных весов, конус и половина шара — на другой.

Заключаем геометрические фигуры в две параллельные плоскости и смотрим, что получается в сечении. У цилиндра — круг с площадью πR2. Как известно, если внутренности геометрических тел не пересекаются, то объем их объединения равен сумме объемов. Пусть в конусе и в половине шара расстояние до плоскости сечения будет x. Радиус — тоже x. Тогда площадь сечения конуса — π ∙ x2. Расстояние от середины верха половины шара к краю сечения — R. Площадь сечения половины шара: π(R2 — x2).

Заметим, что: πR2 + πR2 — πR2 = πR2

Vцил = πR2 × R = πR3 = 1/3 R3 π + Vшара


Vшара = 4/3 πR3

Итак, чтобы найти объем нового, не изученного геометрического тела, нужно сравнить его с тем телом, которое наиболее на него похоже. Многочисленные примеры заданий из открытого банка задач показывают, что в работе с фигурами имеет смысл использовать представленные формулы и аксиомы.

#ADVERTISING_INSERT#

Источник

Добавить комментарий