Как найти объем многоугольной призмы

Определение призмы

Призма — многогранное тело, основаниями которого являются два равных многоугольника, лежащие в параллельных плоскостях. Остальными гранями являются параллелограммы.

Такие параллелограммы в призме называются боковыми.

Онлайн-калькулятор объема призмы

Призмы разделяют на некоторые типы:

1. Треугольная призма — у нее основания — треугольники;
2. Четырехугольная призма — у нее основания — четырехугольники;
3. Пентапризма — пятиугольная призма.

Деление, в общем, продолжается до бесконечности.

Виды призм

Прямая — у такой призмы боковые грани образуют с основаниями прямой угол.
Правильная — ее основанием является какой-либо правильный многоугольник.
Усеченной называется призма, у которой основания не параллельны друг другу.

Формула объема призмы

Объем прямой призмы находится так же, как и объем других многогранников — путем умножения площади основания на высоту.

Объем призмы

V=Sосн⋅hV=S_{text{осн}}cdot h

SоснS_{text{осн}} — площадь основания призмы;
hh — высота призмы.

Разберем задачу на нахождение объема прямой призмы.

Задача

Найти объем призмы, если ее основанием является равнобедренный треугольник с равными сторонами по 5 см5text{ см} и основанием в 6 см6text{ см}. Высота призмы равна 10 см10text{ см}.

Решение

a=5a=5
b=6b=6
h=10h=10

Вычисляем площадь основания. Нужно провести высоту в данном равнобедренном треугольнике. Тогда, по теореме Пифагора, получаем:

a2=l2+(b2)2a^2=l^2+Big(frac{b}{2}Big)^2,

где ll — высота равнобедренного треугольника.

Отсюда:

l2=a2−(b2)2l^2=a^2-Big(frac{b}{2}Big)^2

l=a2−(b2)2l=sqrt{a^2-Big(frac{b}{2}Big)^2}

l=25−9l=sqrt{25-9}

l=4l=4

Площадь равнобедренного треугольника SS это половина от произведения его основания на высоту:

S=12⋅b⋅l=12⋅6⋅4=12S=frac{1}{2}cdot bcdot l=frac{1}{2}cdot 6cdot 4=12

В нашем случае этот треугольник является основанием призмы, поэтому:

S=SоснS=S_{text{осн}}

Тогда объем призмы найдется по формуле:

V=Sосн⋅h=12⋅10=120 см3V=S_{text{осн}}cdot h=12cdot 10=120text{ см}^3

Ответ

120 см3.120text{ см}^3.

На нашем сайте вы можете оформить решение задач на заказ по самым низким ценам!

Тест по теме «Объем призмы»

В данной публикации мы рассмотрим, как можно найти объем призмы и разберем примеры решения задач для закрепления материала.

• Формула вычисления объема призмы

• Примеры задач

Формула вычисления объема призмы

Объем призмы равняется произведению площади ее основания на высоту.

V = S_осн ⋅ h

• S_осн – площадь основания, т.е. в нашем случае – четырехугольника ABCD или EFGH (равны между собой);
• h – высота призмы.

Приведенная выше формула подходит для следующих видов призм: 

• прямой – боковые ребра перпендикулярны основанию;
• правильной – прямая призма, основанием которой является правильный многоугольник;
• наклонной – боковые ребра расположены под углом по отношению к основанию.

Примеры задач

Задание 1
Найдите объем призмы, если известно, что площадь ее основания равна 14 см², а высота – 6 см.

Решение:
Подставляем в формулу известные нам значения и получаем:
V = 14 см² ⋅ 6 см = 84 см³.

Задание 2
Объем призмы равняется 106 см³. Найдите ее высоту, если известно, что площадь основания составляет 10 см².

Решение:
Из формулы расчета объема следует, что высота равняется объему, разделенному на площадь основания:
h = V / S_осн = 106 см³ / 10 см² = 10,6 см.

Что такое призма

Призма — это трехмерное геометрическое тело с двумя равными основаниями и плоскими гранями. Название зависит от фигуры, которая лежит в ее основании. Например, если это треугольник, призму называют «треугольной».

Эта объемная фигура может быть нескольких видов:

1. Прямая. То есть с боковыми ребрами, перпендикулярными основанию.
2. Правильная. В основании лежит правильный многоугольник.
3. Наклонная. Ее ребра расположены под углом к основанию.

Формулы вычисления объема правильной призмы

Правильные призмы могут быть разных видов, в зависимости от многоугольника, который лежит в их основании. Формула вычисления объема во всех случаях выглядит одинаково:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

(V=Scdot h)

Разница лишь в том, каким образом находится площадь S для каждой из фигур.

Треугольная

Чтобы вычислить объем призмы, в основании которой лежит правильный треугольник, используем формулу:

(V=frac{sqrt3}4cdot a^2cdot h)

Где (frac{sqrt3}4cdot a^2=S) — площадь правильного треугольника в основании, a — сторона треугольника, h — высота всей фигуры.

Четырехугольная  

Для фигуры, в основании которой лежит квадрат, используем следующую формулу для вычисления объема:

(V=a^2cdot h)

Где a — сторона квадрата.

Пятиугольная

В этом случае объем будет вычисляться по формуле:

(V=frac52cdot acdotsqrt{left(frac a{2sinleft({displaystylefracpi5}right)}right)^2-frac{a^2}4}cdot h\)

Шестиугольная

Для призмы с правильным шестиугольником в основании формула объема выглядит так:

(x = V=frac{3sqrt3}2cdot a^2cdot h\)

Объем наклонной и прямой

Он находится через произведение площади основания на высоту:

(V=Scdot h\)

Таким образом, формула вычисления объема совпадает с предыдущими вариантами и зависит лишь от фигуры в основании.

С прямой призмой все то же самое. Сначала нужно вычислить площадь ее основания, а потом умножить на высоту.

Примеры задач

Решение:

Так как уже дана площадь основания, нам не важно какая фигура лежит в основании. Подставляем известные значения в формулу:

(V=Scdot h=12cdot5=60 ) (см^3)

Ответ: V=60 (см^3.)

Решение:

Так как сначала для вычисления объема нам нужно определить площадь четырехугольника, будем использовать уравнение: (V=acdot bcdot h)

Подставляем значения: (V=6cdot3cdot10=180) (см^3)

Ответ: V=180 (см^3.)

На этой странице вы узнаете

• Чем упаковка стикеров похожа на призму?
• Как можно попасть в призму в реальной жизни?
• Как сложить игральные кости из листа бумаги?
• Как найти объем воды в аквариуме? 

Слышали такое выражение «смотреть сквозь призму чего-либо»? Оно значит ситуацию, в которой мы воспринимаем что-либо под влиянием каких-то убеждений или представлений. Замысловато, конечно… Возможно, потому что и сама призма — непростое понятие. Давайте разберемся с ней с точки зрения математики.

Определение призмы

Многие из нас пользуются стикерами. Для записи своих дел, для закладок, для пометок при ведении конспектов. Даже если мы ими не пользуемся, то наверняка видели их в магазинах или у родственников и друзей. 

Один такой стикер можно принять за плоскость. Теперь вспомним, как выглядит упаковка с ними. Много-много стикеров накладываются друг на друга и получается небольшая объемная фигура, сверху и снизу которой лежат два абсолютно одинаковых листа. При этом сразу заметим, что нижний и верхний стикеры будут параллельны друг другу. 

На самом деле, упаковка со стикерами является не чем иным, как призмой! 

Призма — это многогранник, в котором две грани являются равными многоугольниками и лежат в параллельных плоскостях, а все остальные — параллелограммами. 

Определение может показаться немного запутанным, но в нем нет ничего страшного. Разберемся, поближе взглянув на составные призмы. 

Строение призмы

Представим себе обычную коробку. Ее дно и крышка равны между собой и лежат в параллельных плоскостях. Это и есть равные многоугольники. Также их называют основаниями призмы. 

Посмотрим на стенки коробки. Они являются параллелограммами, просто с прямыми углами. Подробнее про параллелограммы можно прочитать в статье «Параллелограмм». Эти параллелограммы называются боковыми гранями призмы. 

Возьмем линейку и измерим расстояние между основаниями призмы. Для этого из любой точки одного основания проведем перпендикуляр к другому. 

Подробнее про расстояния между плоскостями можно узнать в статьях «Углы в пространстве» и «Расстояния между фигурами». 

Может возникнуть вопрос, что мы сейчас нашли? Мы нашли высоту призмы. 

Высота призмы — перпендикуляр, опущенный из любой точки одного основания на другое основание призмы. 

В задачах намного удобнее опускать перпендикуляр не из произвольной точки, а из вершины призмы. 

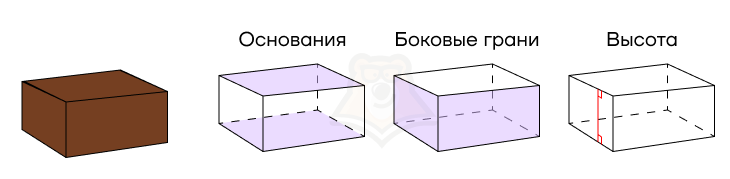
Рассмотрим элементы призмы. 

Ребро — это линия пересечения двух плоскостей. 

Представим, что вместо картонных стенок в нашей коробке ткань, которую нам нужно натянуть на каркас так, чтобы коробка не изменилась. В этом случае все прямые этого каркаса и будут ребрами.

Ребра бывают двух видов: 

• ребра оснований,
• боковые ребра. 

Отличить их также легко: ребра основания являются стороной многоугольника, который в нем лежит, в то время как боковые ребра не принадлежат основаниям. 

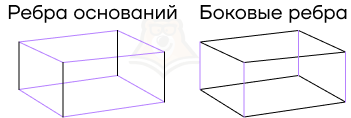
У боковых ребер есть одно очень важное свойство: они равны между собой и параллельны. 

Диагональ призмы — отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. 

Например, мы можем взять клетку попугая и от угла до угла сделать ему жердочку, чтобы птичке было весело жить. Эта жердочка и будет диагональю призмы. 

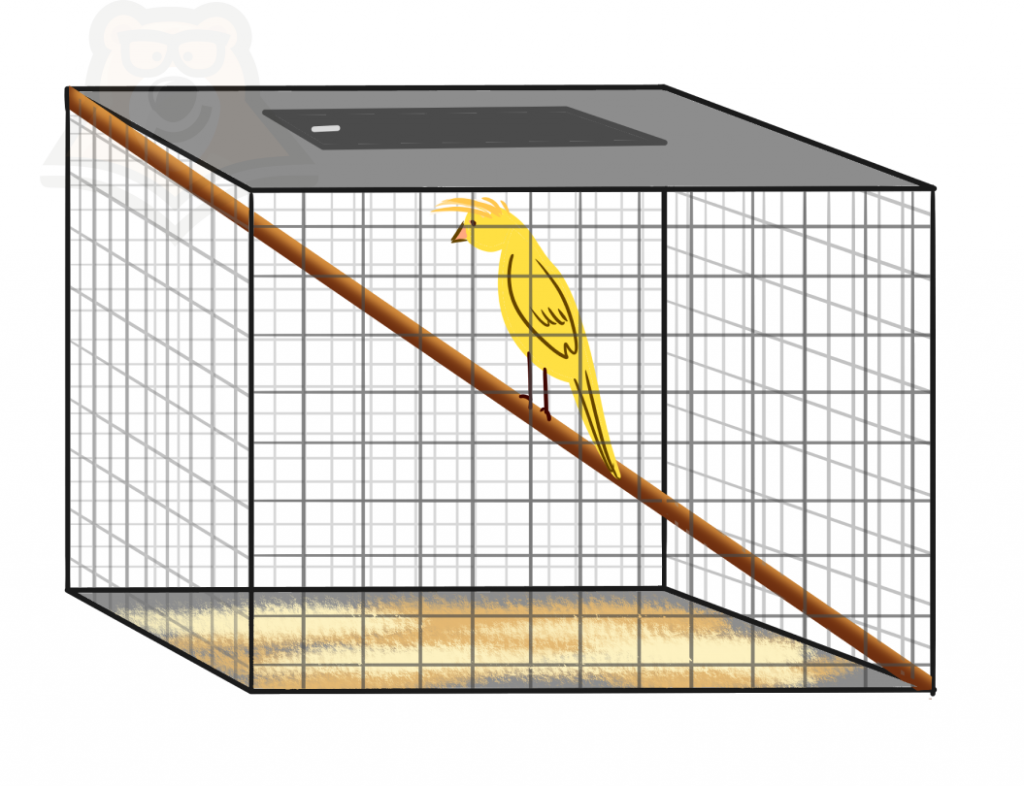
Виды призм

Вернемся к рассуждениям о том, чем упаковка стикеров похожа на призму. Например, куб и параллелепипед будут отличаться. А если в основании призмы будет лежать треугольник или шестиугольник? Или двадцатиугольник? Разделим призмы на несколько видов.

Мы рассмотрим две классификации. 

В первом случае будем рассматривать призмы по фигурам, которые лежат в основании. В многоугольнике может быть множество сторон, а значит, и в основании призмы может быть треугольник, четырехугольник, шестиугольник, десятиугольник и так далее. 

В зависимости от фигуры в основании призмы могут называться по-разному. Вот три основных, которые чаще всего встречаются при решении заданий:

• треугольная призма,

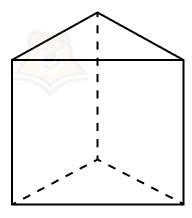
• четырехугольная призма,

• шестиугольная призма. 

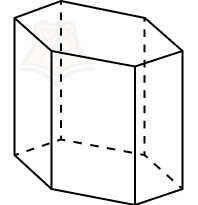
Аналогичным образом можно дать название любой призме, например, десятиугольная призма или стоугольная призма. 

В определении призмы сказано, что в боковых гранях лежат параллелограммы. До этого мы чертили только прямоугольники, но в боковых гранях могут лежать не только они. 

С этим связана вторая классификация призм. По этому признаку призмы делятся всего на два вида:

• прямые,
• наклонные. 

Разберемся в них чуть подробнее. 

Прямая призма — призма, боковые ребра которой перпендикулярны основаниям. 

В этом случае боковые ребра и ребра оснований действительно образовывают прямоугольник. 

Наклонная призма — призма, боковые ребра которой находятся под углом к основаниям. 

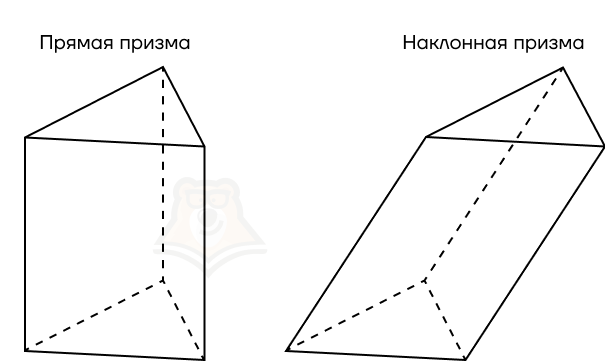
Где мы можем найти прямые и наклонные призмы? Оказывается, в архитектуре. Обычный жилой дом типовой застройки будет прямой призмой. А вот примером наклонной призмы может служить комплекс зданий “Ворота Европы” в Мадриде. 

Чуть подробнее остановимся на прямых призмах. Они встречаются достаточно часто и обладают несколькими важными свойствами. 

Посмотрите на свою комнату. Если по плану квартиры она будет многоугольником, то вы как бы сидите в призме. Теперь ответим на вопрос: как найти высоту комнаты? 

Простой ответ: померить по стене. А если посмотреть на угол, то можно заметить, что ребро призмы совпадает с высотой. Таким образом, мы получаем первое свойство прямых призм. 

Свойство 1. Высота прямой призмы совпадает с её боковым ребром. 

Посмотрим на стены комнаты, на их форму. Они все являются прямоугольниками, верно? 

Свойство 2. Все боковые грани прямой призмы — прямоугольники. 

Если мы в основании прямой призмы разместим правильный многоугольник, у нас получится правильная призма.

Правильная призма — прямая призма, в основании которой лежит правильный многоугольник. 

Например,  в правильной треугольной призме будет лежать равносторонний треугольник, а в правильной шестиугольной призме — правильный шестиугольник. 

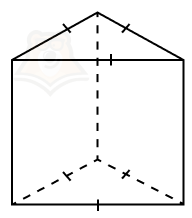
Определение параллелепипеда

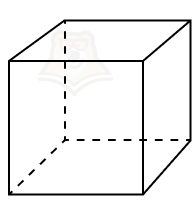
Еще одной разновидностью прямоугольной призмы является параллелепипед. 

Параллелепипед — это четырехугольная призма, все грани которой являются параллелограммами. 

Параллелепипеды встречаются повсюду: коробки, мебель, комнаты, здания, склады, магазины. Поэтому изучить их не составит труда. 

Свойство параллелепипеда, видимое невооруженным глазом: противоположные грани параллелепипеда равны. Как пример, вспомним ту же комнату: потолок и пол равны, так же как и стены, находящиеся напротив друг друга. 

Нельзя не упомянуть про одно очень важное свойство параллелепипеда: 

• Все его диагонали пересекаются в одной точке и этой точкой делятся пополам. Это свойство справедливо для всех видов параллелепипеда. 

Какие бывают параллелепипеды? 

Параллелепипеды также бывают прямыми и наклонными. В этих случаях все определения такие же, как и для всех остальных призм. 

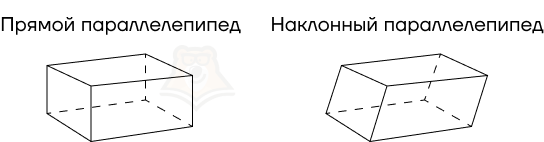
Прямой параллелепипед

Рассмотрим несколько интересных свойств прямого параллелепипеда. 

1 свойство. Боковые ребра прямого параллелепипеда перпендикулярны основаниям. 

2 свойство. Высота прямоугольного параллелепипеда равна длине его бокового ребра. 

3 свойство. Боковые грани, которые лежат напротив друг друга, равны между собой и являются прямоугольниками. 

Прямые параллелепипеды можно разделить еще на два вида:

• Прямой параллелепипед: в основании лежит параллелограмм;

• Прямоугольный параллелепипед: в основании лежит прямоугольник. 

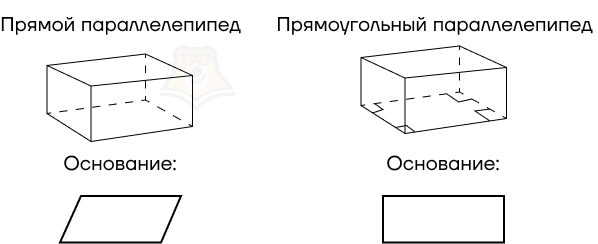
Рассмотрим свойства прямоугольного параллелепипеда. 

1 свойство. Все грани прямоугольного параллелепипеда являются прямоугольниками. 

2 свойство. Все углы в прямоугольном параллелепипеде, образованные двумя гранями, равны 90°. 

3 свойство. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин его ширины, длины и высоты. 

Таким образом, мы получаем важную формулу для параллелепипеда. 

d² = a² + b² + c²

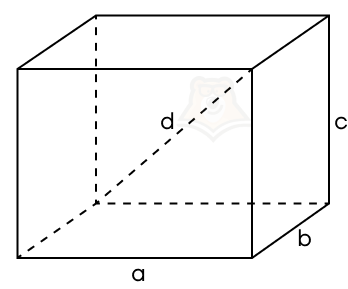
Пример 1. Дан прямоугольный параллелепипед. Два ребра, выходящие из одной его вершины, равны (sqrt{35}) и (sqrt{46}). Диагональ параллелепипеда равна 15. Найдите третье ребро параллелепипеда. 

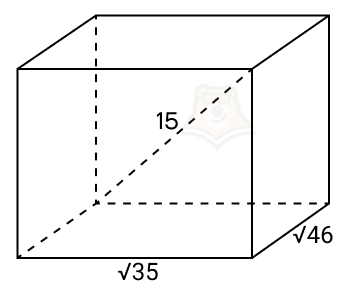
Решение. Пусть третье ребро параллелепипеда равняется х. Получаем уравнение:

(15^2 = (sqrt{35})^2 + (sqrt{46})^2 + x^2)
225 = 35 + 46 + x²
x² = 144
x = 12

Ответ: 12. 

У прямоугольного параллелепипеда существует еще несколько видов. Прямоугольные параллелепипеды делятся на:

• Произвольный прямоугольный параллелепипед. В основании может лежать прямоугольник. 

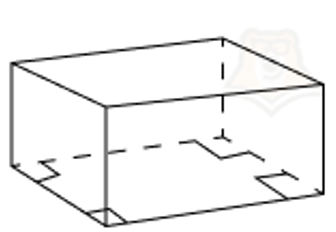
• Правильный прямоугольный параллелепипед. В основании лежит правильный четырехугольник, то есть квадрат. 
  При этом боковые ребра не равны ребрам основания. Следовательно, в основаниях будут лежать квадраты, а в боковых гранях прямоугольники. 

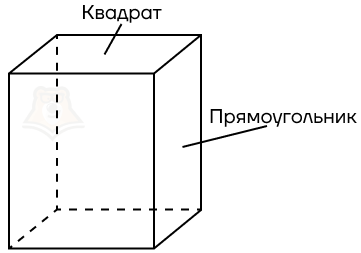
• Куб. В основании лежит квадрат, а боковые ребра равны ребрам основания. 
  В кубе все ребра равны, а все его грани будут квадратом. 

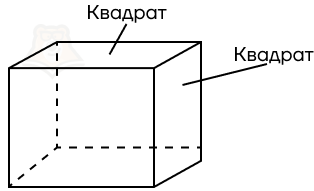
Таким образом, мы рассмотрели все виды параллелепипеда. 

Формулы для призмы

Однако ни одна задача не может быть решена без формул. Поэтому необходимо рассмотреть несколько основных формул, которые могут встретиться не только в задачах, но и в жизни. 

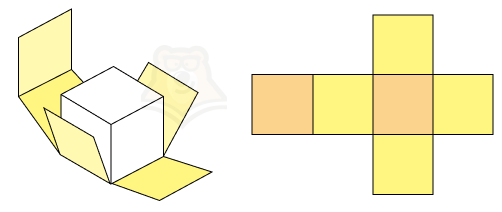
Немного вспомним моделирование, а именно развертку кубика. Мы знаем, что из листа бумаги без труда можно сложить кубик, если правильно его вычертить. 

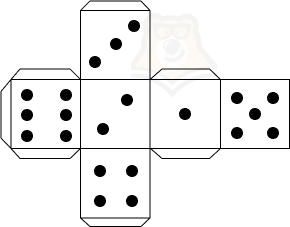
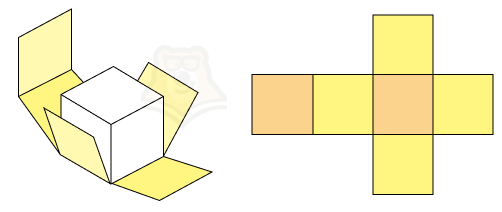
На рисунке оранжевым показаны основания, а желтым боковые грани нашего будущего кубика. А теперь представим, что нам нужно найти площадь боковой поверхности. Как это сделать?

Нужно найти площади желтых квадратиков и сложить их. 

Площадь боковой поверхности призмы — сумма площадей всех боковых ее граней. 

Единой формулы тут нет, поскольку призмы могут очень сильно отличаться друг от друга. В произвольных призмах придется считать площадь каждой боковой грани, а уже после их складывать. 

Но есть один фокус! Правда, он работает только для прямой призмы. Если по условию дана прямая призма, то можно воспользоваться формулой 

S_бок. = P * h

В этой формуле Р — периметр основания, h — высота призмы, которая совпадает с высотой боковой грани. 

Пример 1. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равняется 2, а высота 10. 

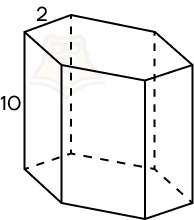
Решение. 

Шаг 1. Поскольку правильная призма по определению прямая, мы можем воспользоваться формулой S = Ph. 

Шаг 2. В основании правильной призмы лежит правильный шестиугольник, следовательно, периметр основания будет равен 6 * 2 = 12. 

Шаг 3. Осталось найти только площадь боковой поверхности. Подставляем данные в формулу и получаем: S = 12 * 10 = 120. 

Ответ: 120. 

Пример 2. Дана прямая треугольная призма, в основании которой лежит прямоугольный треугольник с катетами 12 и 5. Высота призмы равна 13. Найдите площадь ее боковой поверхности. 

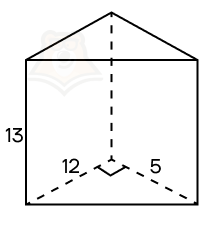
Решение. 

Шаг 1. Поскольку призма прямая, можно воспользоваться формулой S = Ph. 

Шаг 2. Найдем периметр основания. Для этого необходимо найти гипотенузу треугольника. Воспользуемся теоремой Пифагора: (sqrt{12^2 + 5^2} = sqrt{144 + 25} = sqrt{169} = 13). 

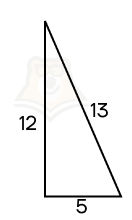
Шаг 3. Найдем периметр основания: P = 12 + 5 + 13 = 30. 

Шаг 4. Осталось найти только площадь боковой поверхности. Подставляем данные в формулу и получаем: S = 30 * 13 = 390. 

Ответ: 390. 

Мы научились находить площадь боковой поверхности. А как найти всю площадь призмы? Вспомним нашу развертку с кубиком. Чтобы найти всю площадь кубика, нужно найти площадь всех квадратов, из которых он состоит. То есть и площадь боковой поверхности, и площадь оснований. 

Площадь полной поверхности призмы — сумма площадей всех граней. 

Следовательно, нам нужно сложить площади всех боковых граней и дважды площадь основания. Получаем следующую формулу. 

S = S_бок + 2S_осн

Вспомним обычный хлеб, черный или белый. Его форма очень приближена к параллелепипеду. Тогда его корочка будет площадью полной поверхности параллелепипеда. А все что внутри, то есть мякиш, можно принять за объем. 

Пример 3. Дана прямая призма, в основании которой лежит ромб с диагоналями 12 и 16. Боковое ребро призмы равно 25. Найдите площадь поверхности призмы. 

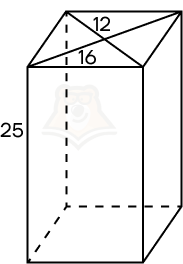
Решение. 

Шаг 1. Найдем площадь основания. Площадь ромба можно найти по формуле (frac{1}{2} * D_1 * D_2). Следовательно, площадь ромба равна (frac{1}{2} * 12 * 16 = 96). 

Шаг 2. Заметим, что диагонали ромба образуют четыре равных прямоугольных треугольника. Следовательно, чтобы найти сторону ромба, достаточно рассмотреть прямоугольный треугольник с катетами 6 и 8. По теореме Пифагора сторона ромба будет равна (sqrt{6^2 + 8^2} = sqrt{36 + 64} = sqrt{100} = 10).

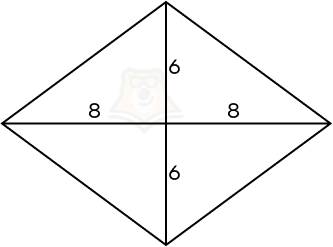
Шаг 3. Периметр ромба будет равен 4 * 10 = 40. Тогда площадь боковой поверхности равна 40 * 25 = 1000. 

Шаг 4. Площадь полной поверхности будет равняться 1000 + 2 * 96 = 1000 + 192 = 1192.

Ответ: 1192

Пример 4. Площадь поверхности правильной четырехугольной призмы равняется 1980. Сторона основания равна 5. Найдите боковое ребро этой призмы. 

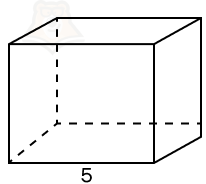
Решение. 

Шаг 1. Воспользуемся формулой S = S_бок + 2S_осн. Площадь основания будет равняться площади квадрата, то есть 5 * 5 = 25. 

Шаг 2. Подставим известные величины в формулу: 

1980 = S_бок + 2 * 25
S_бок = 1930

Шаг 3. Площадь боковой поверхности равна произведению периметра основания на высоту призмы. Периметр равен 5 * 4 = 20. Тогда получаем уравнение:

20h = 1930
h = 96,5

Шаг 4. Поскольку по условию дана правильная призма, то высота совпадает с боковым ребром. Следовательно, боковое ребро равняется 96,5.

Ответ: 96,5. 

Теперь рассмотрим, как найти объем призмы. Допустим, мы налили в прямоугольный аквариум немного воды. Как определить, сколько воды мы налили?

Для этого достаточно воспользоваться формулой объема призмы. 

V = S_осн. * h

Эта формула общая, однако для каждой призмы она может принять свой вид в зависимости от того, какую формулу нужно использовать для поиска площади основания или высоты. 

Например, чтобы найти объем воды в аквариуме, необходимо длину умножить на ширину и на высоту, а значит формула принимает вид V = abh. 

Пример 5. Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 12 и 15. Боковое ребро призмы равно 4. Найдите объем этой призмы. 

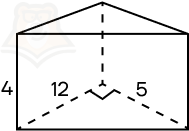
Решение. 

Шаг 1. Для начала найдем площадь основания. В этом случае мы можем воспользоваться формулой (frac{1}{2}ab). Площадь равна (frac{1}{2} * 12 * 15 = 90).

Шаг 2. Воспользуемся формулой объема призмы и подставим известные величины: 

V = 90 * 4 = 360.

Ответ: 360. 

Пример 6. Дан сосуд, в основании которого лежит правильный треугольник. В этот сосуд налили 3000 см³ воды. Высота жидкости оказалась равной 10 см. После этого в сосуд опустили шарик и высота изменилась с 10 см на 14 см. Найдите объем шарика. 

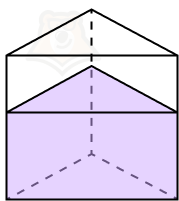
Решение. Немного вспомним физику, а именно тот факт, что объем вытесненной жидкости равен объему тела. Значит, чтобы найти объем шарика, необходимо найти насколько изменился объем воды. 

Шаг 1. Найдем площадь основания сосуда. Для этого немного преобразуем формулу объема: 
(S = frac{V}{h})
Тогда:
(S = frac{3000}{10} = 300)

Шаг 2. А теперь найдем объем после того, как в воду погрузили шарик. Он будет равен 300 * 14 = 4200. 

Шаг 3. Объем вытесненной жидкости равен 4200 — 3000 = 1200.

Ответ: 1200. 

Мы рассмотрели основные формулы, которые применяются для решения задач. Стоит заметить, что они универсальны, и в каждой задаче их рационально преобразовывать под ситуацию. 

Фактчек 

• Призма — это многогранник, в котором две грани являются равными многоугольниками и лежат в параллельных плоскостях, а все остальные — параллелограммами. Равные многоугольники называются основаниями призмы, а остальные стороны — боковыми гранями. В призме есть ребра — линии пересечения двух ее граней. Ребра как бы образуют каркас призмы. 
• Призмы можно разделить на несколько видов по тому, какая фигура лежит в основании: треугольник, четырехугольник, шестиугольник или любой другой многоугольник. Призмы бывают прямые и наклонные. В прямых призмах боковые ребра перпендикулярны основанию, а в наклонных — нет. Правильная призма — прямая призма, в основании которой лежит правильный многоугольник. 
• Параллелепипед — это четырехугольная призма, все грани которой являются параллелограммами. Параллелепипеды бывают наклонными и прямыми. Прямые параллелепипеды включают в себя прямоугольные параллелепипеды, которые, в свою очередь, делятся на произвольные, правильные и кубы. 
• В призме можно найти площадь боковой поверхности, площадь полной поверхности и объем. Для каждого из этих случаев необходимо пользоваться формулами. 

Проверь себя

Задание 1.
Что такое диагональ призмы?

1. Отрезок, соединяющий две соседние вершины в призме.
2. Отрезок, соединяющий противоположные углы в боковой грани призмы.
3. Отрезок, соединяющий противоположные углы в основании призмы.
4. Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.  

Задание 2.
Что такое прямая призма?

1. Призма, боковые ребра которой перпендикулярны основаниям.
2. Призма, боковые ребра которой расположены под острым углом относительно основания.
3. Призма, боковые ребра которой расположены под тупым углом относительно основания.
4. Призма, в основании которой лежит прямоугольник.

Задание 3.
Как найти высоту прямой призмы?

1. Высоту нужно найти с помощью оснований.
2. Высота совпадает с боковым ребром.
3. Необходимо найти расстояние между двумя вершинами, не принадлежащими одной грани.
4. В прямой призме невозможно найти высоту. 

Задание 4.
Какая фигура лежит в основании прямоугольного параллелепипеда?

1. Параллелограмм с острыми углами.
2. Ромб с острыми углами.
3. Трапеция.
4. Прямоугольник. 

Задание 5. 
Как найти площадь полной поверхности призмы?

1. Нужно найти сумму площадей всех боковых граней.
2. Нужно сложить площадь боковой поверхности и площадь основания.
3. Нужно сложить площадь боковой поверхности и удвоенную площадь основания.
4. Нужно сложить площади оснований. 

Ответы: 1. — 4 2. — 1 3. — 2 4. — 4 5. — 3