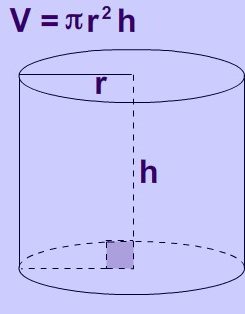
Цилиндр (круговой цилиндр) – тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, – образующими цилиндра.
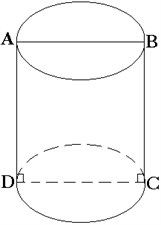
Цилиндр называется прямым, если его образующие перпендикулярны плоскостям основания. Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг одной из сторон как оси. Существуют и другие виды цилиндра – эллиптический, гиперболический, параболический. Призму так же рассматривают, как разновидность цилиндра.
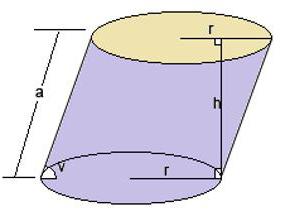
На рисунке 2 изображён наклонный цилиндр. Круги с центрами О и О1 являются его основаниями.
Радиус цилиндра – радиус его основания. Высота цилиндра – расстояние между плоскостями оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим. Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением. Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведённому через эту образующую, называется касательной плоскостью цилиндра.
Плоскость, перпендикулярная оси цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.
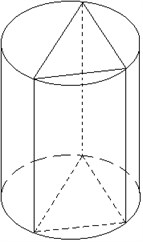
Площадь боковой поверхности цилиндра можно вычислить, умножив длину образующей на периметр сечения цилиндра плоскостью, перпендикулярной образующей.
Площадь боковой поверхности прямого цилиндра можно найти по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой h и длиной P, которая равна периметру основания. Следовательно, площадь боковой поверхности цилиндра равна площади его развёртки и вычисляется по формуле:
Sb = Ph.
В частности, для прямого кругового цилиндра:
P = 2πR, и Sb = 2πRh.
Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований.
Для прямого кругового цилиндра:
Sp = 2πRh + 2πR2 = 2πR(h + R)
Для нахождения объёма наклонного цилиндра существуют две формулы.
Можно найти объём, умножив длину образующей на площадь сечения цилиндра плоскостью, перпендикулярной образующей.
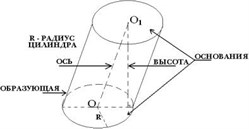
V = Sh = S l sin α,
где l – длина образующей, а α – угол между образующей и плоскостью основания. Для прямого цилиндра h = l.
Формула для нахождения объёма кругового цилиндра выглядит следующим образом:
V = π R2 h = π (d2 / 4)h,
где d – диаметр основания.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Объем наклонного цилиндра с учетом боковой кромки Калькулятор
| Search | ||
| Дом | математика ↺ | |
| математика | Геометрия ↺ | |
| Геометрия | 3D геометрия ↺ | |
| 3D геометрия | Наклонный цилиндр ↺ | |
| Наклонный цилиндр | Объем наклонного цилиндра ↺ |
|
✖Радиус наклонного цилиндра — это расстояние между центром и любой точкой на окружности базовой круглой грани наклонного цилиндра.ⓘ Радиус наклонного цилиндра [r] |
+10% -10% |
||
|
✖Боковой край наклонного цилиндра — это край, образующий боковую грань косого цилиндра.ⓘ Боковая кромка наклонного цилиндра [le(Lateral)] |
+10% -10% |
||
|
✖Угол наклона наклонного цилиндра — это измерение угла, под которым цилиндр опирается на основание наклонного цилиндра.ⓘ Угол наклона косого цилиндра [∠Slope] |
+10% -10% |
|
✖Объем косого цилиндра – это общее количество трехмерного пространства, заключенного во всей поверхности косого цилиндра.ⓘ Объем наклонного цилиндра с учетом боковой кромки [V] |
⎘ копия |
Объем наклонного цилиндра с учетом боковой кромки Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Радиус наклонного цилиндра: 5 метр –> 5 метр Конверсия не требуется
Боковая кромка наклонного цилиндра: 12 метр –> 12 метр Конверсия не требуется
Угол наклона косого цилиндра: 60 степень –> 1.0471975511964 Радиан (Проверьте преобразование здесь)
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
816.209713905305 Кубический метр –> Конверсия не требуется
5 Объем наклонного цилиндра Калькуляторы
Объем наклонного цилиндра с учетом боковой кромки формула
Объем наклонного цилиндра = pi*(Радиус наклонного цилиндра^2)*Боковая кромка наклонного цилиндра*sin(Угол наклона косого цилиндра)
V = pi*(r^2)*le(Lateral)*sin(∠Slope)
Что такое наклонный цилиндр?
Наклонный цилиндр — это тот, который «наклоняется», когда стороны не перпендикулярны основаниям. Напротив «правого цилиндра». В косом цилиндре основания (концы) остаются параллельными друг другу, но стороны наклоняются под углом, не равным 90°. Если они расположены под прямым углом к основаниям, то такой цилиндр называется прямым.
Объем цилиндра
Цилиндр – это твердое тело, состоящее из двух конгруэнтных круглых областей, расположенных в параллельных плоскостях. Он также содержит их внутренности, а также все отрезки, параллельные отрезку, содержащему центр каждого круга, и его конечные точки на круглой области.
[Ознакомьтесь с этой статьей для получения общей информации о цилиндрах. ] (https://www.cuemath.com/geometry/cylinder/)
Объем цилиндра
Объем цилиндра – это его вместимость. Это определяет, сколько материала он может вместить. Конкретный объем цилиндрической формулы используется в геометрии для определения того, сколько жидкости или твердого тела может быть погружено в него. Цилиндр — это трехмерная фигура, имеющая два одинаковых параллельных основания. Есть много типов цилиндров. Эти:
Каков объем цилиндра?
Объем цилиндра относится к числу кубов (кубов с единичной длиной), которые могут поместиться внутри него. Это площадь, занимаемая цилиндром, как и любой трехмерной формой. Кубические единицы используются для измерения цилиндрических объемов, таких как см^3 и м3.
Объем правого кругового цилиндра
Мы знаем, что основанием правильного кругового цилиндра является круг, а площадь круга с радиусом r равна p*r^2. Объем (V) прямоугольного цилиндрического цилиндра рассчитывается по приведенной выше формуле.
r: радиус основания (окружности) цилиндра
p: относится к константе, значение которой может быть либо 22/7, либо 3,142.
Объем цилиндра напрямую зависит от его высоты, а также прямо зависит от квадрата его радиуса. Это означает, что если радиус станет вдвое больше диаметра цилиндра, то его объем увеличится в четыре раза.
Объем наклонного цилиндра
Формула для вычисления объема наклонного цилиндра такая же, как и для вычисления объема в прямоугольном цилиндрическом цилиндре. Объем (V) наклонного цилиндра, радиус основания и высота которого равны «r», а высота «h» такая же, как и у прямого кругового цилиндра.
Объем эллиптического цилиндра
Известно, что эллипс имеет два радиуса. Мы также знаем, что площадь эллипса с радиусом «а» или «b» равна p*a*b. Объем эллиптического цилиндра равен,
a, b: радиус основания (эллипса) цилиндра
p: константа, значение которой может быть либо 22/7, либо 3,142.
Объем правого круглого полого цилиндра
Правильный круглый полый цилиндр состоит из двух правильных круглых полых цилиндров, соединенных друг с другом внутри. Его объем можно рассчитать, вычитая объем из внешнего цилиндра. Объем (V) прямоугольного полого цилиндра равен .
V = p (R ^ 2 – r ^ 2) * ч
R: Радиус, на котором основание внешнего цилиндра встречается
r: радиус основания внутренней цилиндрической
p: константа, значение которой может быть либо 22/7, либо 3,142.
Таблица преобразования и единиц объема
Вот самые популярные единицы объема:
Автор статьи
Parmis Kazemi
Пармис – создатель контента, который любит писать и создавать новые вещи. Она также очень интересуется технологиями и любит узнавать что-то новое.
Калькулятор Объема Цилиндра русский
Опубликовано: Thu Mar 10 2022
В категории Математические калькуляторы
Добавьте Калькулятор Объема Цилиндра на свой сайт
Здание Планетария Тихо Браге, Копенгаген, его крыша является примером цилиндрического сечения
Цили́ндр (др.-греч. κύλινδρος — валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Связанные определения[править | править код]
- Цилиндрическая поверхность — поверхность, образуемая однопараметрическим семейством параллельных прямых (называемых образующими) и проходящими через точки некоторой кривой (называемой направляющей).
- Плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями, ограничивающими цилиндр, называются основаниями этого цилиндра.
- Часть цилиндрической поверхности, находящаяся между плоскостями оснований, называется боковой поверхностью цилиндра.
- Высотой цилиндра называется отрезок, высекаемый плоскостями его оснований на прямой, перпендикулярной им, или длина этого отрезка.
Типы цилиндров[править | править код]
- Прямым называется цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), прямая между которыми перпендикулярна плоскостям этих оснований. Данная прямая называется осью цилиндра.
- Косым называется цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), отрезок между которыми не перпендикулярен плоскостям этих оснований.
- Круговым называется цилиндр с окружностью в роли направляющей.
- Цилиндром вращения, или прямым круговым цилиндром (часто под цилиндром подразумевают именно его) называется цилиндр, который можно получить вращением (то есть тело вращения) прямоугольника вокруг одной из его сторон, содержащая которую прямая в таком случае будет осью этого цилиндра и его осью симметрии.
- Цилиндр, основания которого являются эллипсами, параболами или гиперболами, называют соответственно эллиптическим, параболическим и гиперболическим; последние два имеют бесконечный объём.
- Призма также является разновидностью цилиндра — с основанием в виде многоугольника.
- Равносторонним называется цилиндр вращения, диаметр основания которого равен его высоте[1].
Свойства[править | править код]
- Если плоскость основания цилиндра параллельна плоскости направляющей, то граница этого основания будет по форме совпадать с направляющей кривой.
Площадь поверхности цилиндра[править | править код]
Площадь боковой поверхности[править | править код]
К вычислению площади боковой поверхности цилиндра
Площадь боковой поверхности цилиндра равна длине образующей, умноженной на периметр сечения цилиндра плоскостью, перпендикулярной образующей.
Площадь боковой поверхности прямого цилиндра вычисляется по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой 

В частности, для прямого кругового цилиндра:
, и
, здесь и далее
— радиус основания цилиндра.
Для наклонного цилиндра площадь боковой поверхности равна длине образующей, умноженной на периметр сечения, перпендикулярного образующей:
Простой формулы, выражающей площадь боковой поверхности косого цилиндра через параметры основания и высоту, в отличие от объёма не существует. Для наклонного кругового цилиндра можно воспользоваться приближёнными формулами для периметра эллипса, а затем умножить полученное значение на длину образующей.
Площадь полной поверхности[править | править код]
Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований.
Для прямого кругового цилиндра:

Объём цилиндра[править | править код]
Для наклонного цилиндра существуют две формулы:
- Объём равен длине образующей, умноженной на площадь сечения цилиндра плоскостью, перпендикулярной образующей.
,
- Объём равен площади основания, умноженной на высоту (расстояние между плоскостями, в которых лежат основания):
,
- где
— длина образующей, а
— угол между образующей и плоскостью основания. Для прямого цилиндра
.
Для прямого цилиндра 


Для кругового цилиндра:

где d — диаметр основания.
Примечания[править | править код]
- ↑ Математический справочник
Вопрос, как найти объем цилиндра, может возникнуть не только у школьника. Ведь такую форму имеет, к примеру, кастрюля, емкость которой иногда срочно нужно узнать. Вот тогда потребуется знание специальной формулы.
Что нужно знать о цилиндре?
Геометрическое тело, о котором мы говорим, образуется в результате вращения прямоугольника вокруг одной из его сторон, и всегда будет прямым. То есть угол между образующей цилиндра и его основанием в данном случае равен 90 градусам. Если выполнить это простое движение не удается, и угол уже не 90 градусов, то идет речь о наклонном цилиндре.
Каким бы ни был вид тела, все равно нужно знать о том, как найти объем цилиндра. Но сначала нужно определиться с некоторыми теоретическими данными.
Как называются отдельные элементы цилиндра и что о них известно?
Отрезки, которые соединяют попарно соответствующие точки на двух основаниях, называются образующими. У любого цилиндра они равны и параллельны друг другу. Если он прямой, то длина образующей совпадает с высотой тела.
В основании может лежать окружность или эллипс, тогда цилиндр будет круговым или эллиптическим соответственно. В формулах этот факт потребуется учесть. Потому что чаще всего они даются для кругового цилиндра. В эллиптическом, до того как вычислить объем цилиндра, нужно будет узнать, по какой формуле определить площадь овала.
Формулы объема для прямого и наклонного цилиндров
Здесь и далее приняты такие обозначения.
| Буква-обозначение | математическая величина |
| V | объем |
| S | площадь основания |
| h | высота |
| r | радиус окружности |
| l | длина образующей |
| α | угол между образующей и основанием |
В любом случае потребуется формула, в которой высота тела, умножается на площадь основания. Она выглядит так:
V = Sh
Если требуется узнать, как найти объем цилиндра прямого, то здесь высота по длине полностью совпадает с образующей. Основанием чаще всего является круг, тогда его площадь будет сосчитана по формуле:
S = πr2.
Когда в задаче идет речь об эллиптическом цилиндре, то потребуется такая формула площади основания:
S = π ab, здесь буквами a и b обозначены малая и большая полуоси овала.
При решении задач о наклонном цилиндре потребуется ввести некоторые дополнения в формулу. Например, если не известна высота, но идет речь об образующей и угле между ней и основанием. Тогда букву h потребуется заменить таким выражением:
h = l * sin α.
Как быть, если нужно определить объем на практике?
В задачах обычно уже известны значения угла или высоты с образующей. А возможно, какие-то другие элементы, через которые их можно найти. В жизни приходится делать измерения самостоятельно.
Тогда вопрос о том, как определить объем цилиндра, сводится к тому, чтобы правильно сделать измерения его высоты и радиуса. Для этого потребуются: линейка, карандаш и прямоугольный лист бумаги.
Чаще всего в быту нас окружают прямые круговые цилиндры. Измерить их высоту обычно не составляет труда. Нужно просто приложить линейку сбоку и измерить расстояние от низа до верха тела. Это будет высота — h.
С радиусом окружности все не так легко. Нужно немного вспомнить геометрию. Здесь потребуется лист бумаги с прямым углом и карандаш.
Что дает теория по геометрии? Вокруг прямоугольного треугольника можно описать окружность. Причем его прямой угол окажется на ней, а гипотенуза совпадет с диаметром.
Нужно взять лист бумаги и положить его так, чтобы прямой угол касался края основания. Тогда две его стороны, которые образуют этот угол, в некоторых точках пересекутся с окружностью. В этих местах потребуется сделать метки. По ним провести отрезок. Он окажется гипотенузой и искомым диаметром основания цилиндра.
Как найти объем цилиндра, в нашем случае? В формуле фигурирует радиус. Он равен половине диаметра. То есть длину получившегося отрезка нужно разделить на два.
Осталось только подставить результаты измерений в формулу объема и сосчитать. Причем учесть, что ответ получится в см3. Если объем нужно узнать в кубических метрах, то число нужно будет разделить на миллион. Чтобы получить объем в литрах, делителем окажется тысяча.
Задача
Условие. Даны два цилиндра. Высота первого в два раза больше второго. Радиус второго вдвое больше, чем у первого. Необходимо узнать, во сколько раз объем первого цилиндра больше или мегьше объема второго.
Решение. Сначала потребуется ввести обозначения. Пусть высота и радиус первого тела будут иметь индекс 1, а второго — 2.
Теперь можно записать данные в условии значения в виде выражений:
h1 = 2h2 и r2 = 2r1.
Формулы объемов обоих цилиндров примут такой вид:
v1 = π r12 h1 и v2 = π r22 h2.
В задаче требуется найти:
v1 : v2 = (π r12 h1) : (π r22 h2).
После сокращения πи замены h1 и r2введенными выражениями, получается:
v1 : v2 = (r12 2h2) : (4r12 h2).
То есть v1 : v2 = 1 : 2. Это означает, что объем первого цилиндра в два раза меньше.
Ответ. v1 = v2 : 2.