Наклонная призма — это призма, боковые рёбра которой не перпендикулярны основанию.

— основания призмы.
— бoковые грани. Вcе бoковые грани наклонной призмы являются параллелограммами.
— боковые рёбра. Боковые рёбра параллельны между собой и равны.
— высота наклонной призмы (перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания). Часто перпендикуляр проводят с одной из вершин верхнего основания.
— угол между боковым ребром и плоскостью основания.
Площадью боковой поверхности наклонной призмы называется сумма площадей её боковых граней.
Площадью полной поверхности наклонной призмы называется сумма площадей всех её граней.
Объём наклонной призмы равен произведению площади основания на высоту
Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра.
Объём наклонной призмы равен площади перпендикулярного сечения на боковое ребро.
Перпендикулярное сечение — пересечение призмы и плоскости, перпендикулярной её боковому ребру.
Источники:
Рис. 1. Наклонная призма, © ЯКласс.
Сегодня на уроке мы выведем формулу для нахождения
объёма наклонной призмы.
Прежде чем приступить к изучению нового материала
давайте вспомним формулу для нахождения объёма геометрического тела ,
повторим формулу для вычисления объёма прямой призмы .
Давайте сформулируем и докажем теорему.
Объём наклонной призмы равен произведению площади
основания на высоту.
Доказательство.
Сначала докажем эту теорему для треугольной наклонной призмы.
Рассмотрим треугольную призму с объёмом ,
площадью основания и
высотой .
Отметим на одном из оснований призмы точку и
направим ось перпендикулярно
основаниям.
Рассмотрим сечение призмы плоскостью,
перпендикулярной к оси и,
значит, параллельной плоскости основания. Обозначим буквой абсциссу
точки пересечения этой плоскости с осью ,
а через –
площадь получившегося сечения.
Теперь давайте покажем, что площадь .
Четырёхугольник –
параллелограмм, значит, .
Аналогично, четырёхугольник –
параллелограмм, значит, .
Четырёхугольник –
параллелограмм, значит, и отрезки .
Тогда получим, что треугольники по
трём сторонам, то есть мы доказали, что площади этих треугольников равны .
Теперь давайте применим основную формулу для
вычисления объёмов тел .
Теперь давайте докажем эту теорему для произвольной
призмы высоты и
площадью основания .
Такую призму можно разбить на треугольные призмы с
общей высотой .
Рассмотрим, например, выпуклую пятиугольную призму.
Вычислим объём каждой полученной треугольной призмы
по доказанной нами формуле. Мы знаем, что если тело
составлено из нескольких тел, то его объём равен сумме объёмов этих тел.
Тогда объём нашей пятиугольной призмы равен сумме
объёмов треугольных призм.
Поскольку мы разбивали пятиугольную призму на
треугольные с общей высотой, то в сумме объёмов высоту можно вынести за скобки.
В скобках получим сумму площадей треугольников, на которые мы разбили
пятиугольник. То есть в скобках мы получили площадь пятиугольника, который
лежит в основании призмы. Тогда получим, что объём наклонной призмы равен ,
что и требовалось доказать.
Но объём наклонной призмы можно вычислить по другой
формуле.
Объём наклонной призмы равен .
Эту формулу мы доказывать не будем, просто рассмотрим несколько задач и
посмотрим случаи, в которых проще вычислить объём призмы именно с помощью этой
формулы.
Решим несколько задач.
Задача:
найти объём наклонной призмы, у которой основанием является треугольник со
сторонами ,
,
,
а боковое ребро, равное ,
составляет с плоскостью основания угол в .
Решение:
для вычисления объёма призмы, воспользуемся только что доказанной формулой.
Площадь основания вычислим по формуле Герона.
Получим, что площадь основания призмы равна
Теперь давайте проведем высоту призмы и рассмотрим .
Так как –
высота, значит, треугольник прямоугольный. По условию, боковое ребро равно ,
а угол между боковым ребром и плоскостью основания равен .
Это будет угол между боковым ребром призмы и его ортогональной проекцией на
плоскость основания. В данном случае, это будет ,
тогда .
По свойству катета, лежащего напротив угла в тридцать градусов, .
Тогда по теореме Пифагора нетрудно найти чему равна высота призмы. Высота
призмы равна .
Подставим найденные значения в формулу для вычисления
объёма призмы и получим, что объём призмы равен .
Задача:
найти объём наклонной призмы, основанием которой является параллелограмм .
Сторона ,
сторона ,
.
Высота призмы равна .
Решение:
воспользуемся только что доказанной формулой.
Для вычисления площади параллелограмма, лежащего в
основании, воспользуемся формулой: .
Площадь основания будет равна .
Подставим полученное значение в формулу для
вычисления объёма, получим, что объём призмы равен .
Задача:
найти объём наклонной треугольной призмы, если расстояния между ее боковыми рёбрами
равны ,
и
,
а площадь боковой поверхности равна .
Решение:
расстояния между боковыми рёбрами – длина перпендикуляров. Таким образом,
проведя все перпендикуляры мы получим треугольник, который будет
перпендикулярным сечением призмы.
Поэтому нетрудно увидеть, что для вычисления объёма
мы воспользуемся тем, что объём наклонной призмы равен .
Но прежде вспомним, что площадь боковой поверхности
наклонной призмы равна .
Периметр перпендикулярного сечения равен .
Тогда длина бокового ребра равна .
Вычислим площадь перпендикулярного сечения по
формуле Герона. Получим, что площадь сечения равна
Подставим полученные значения в формулу для
вычисления объёма и получим, что объём призмы равен .
Итоги:
Сегодня на уроке мы вывели формулу для вычисления
объёма наклонной призмы.
Показали ещё одну формулу для вычисления объёма
наклонной призмы. Решили несколько задач.
Конспект урока: Объём наклонной призмы
Объем
План урока
- Объём наклонной призмы;
- Примеры.
Цели урока
- Знать формулу объёма наклонной призмы;
- Уметь применять формулу объёма наклонной призмы для решения задач.
Разминка
- Чему равен объём правильной четырехугольной призмы, сторона основания которой равна 3, а боковое ребро – 4?
- Объём какой фигуры равен произведению площади основания на высоту?
Объём наклонной призмы
Наклонная призма — это призма, боковые рёбра которой не перпендикулярны основанию. Объём прямой призмы мы находить умеем. Также известно, что объём тела можно вычислить с помощью интеграла по формуле: V=∫abSxdx.
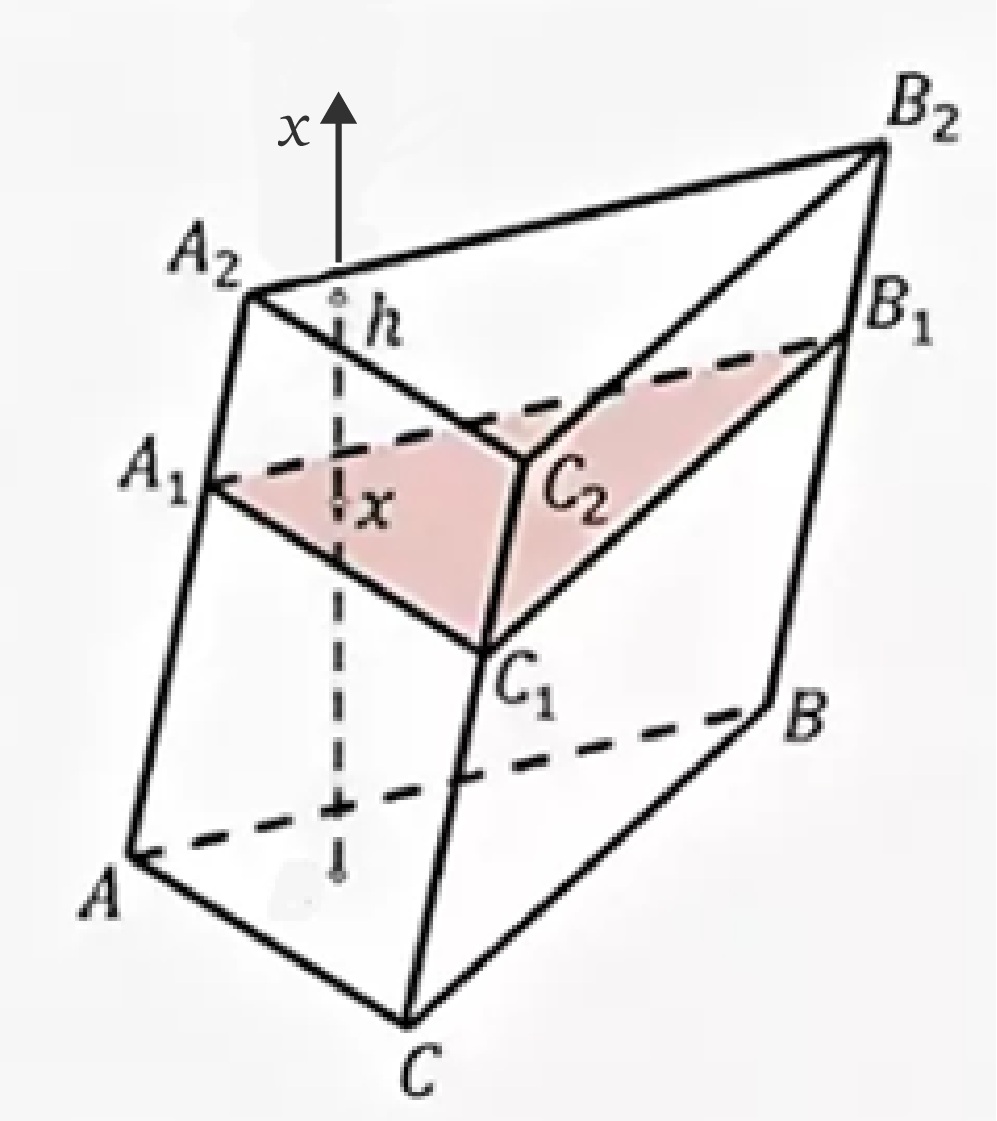
Рис. 1. Наклонная треугольная призма
Воспользуемся этой формулой для нахождения объёма наклонной треугольной призмы.
Рассмотрим наклонную треугольную призму ABCA2B2C2 (рис. 1). Пусть площадь основания этой призмы S, а высота h. Найдем её объём. Отметим точку O на одном из оснований и направим ось Ox перпендикулярно к основаниям. Построим сечение A1B1C1 перпендикулярно высоте призмы, при этом x – абсцисса точки пересечения этой плоскости с высотой призмы. Обозначим площадь сечения через Sx.
Тогда, используя формулу объёма через определенный интеграл, получим, что объём призмы равен:
V=∫0hSxdx.
Обратим внимание, что высота призмы перпендикулярна плоскостям основания, а также построенной плоскости. Следовательно, плоскости ABC и A1B1C1 параллельны, значит, AC∥A1C1, AB∥A1B1 и BC∥B1C1. Тогда ACC1A1, ABB1A1 и BCC1B1 – параллелограммы, т.е. AC=A1C1, AB=A1B1 и BC=B1C1. Значит, треугольники ABC и A1B1C1 равны, соответственно равны и их площади S=Sx. Таким образом площадь любого сечения, которое перпендикулярно высоте наклонной призмы, равна площади основания.
Тогда формула объёма примет следующий вид:
V=∫0hSxdx=∫0hSdx=S∫0hdx=S·x0h=S·h.
Получили, что объём наклонной треугольной призмы равен произведению площади основания на высоту.
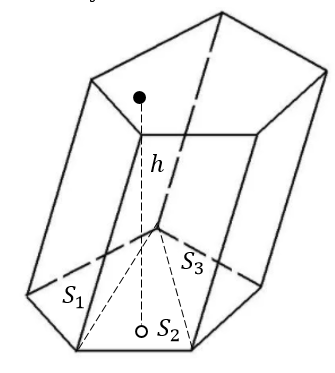
Рис. 2. Наклонная призма
Теперь рассмотрим произвольную наклонную призму с площадью основания S и высотой h. Можем разбить эту призму на треугольные призмы с высотой h (на рис. 2. разбиение выпуклой пятиугольной призмы). Объём каждой из них равен произведению площади основания на высоту. Объём призмы равен сумме объёмов треугольных призм, а площадь основания равна сумме площадей оснований треугольных призм. Тогда
V=S1·h+S2·h+S3·h=S1+S2+S3·h=S·h.
Мы доказали следующую теорему.
Теорема
Объём наклонной призмы равен произведению площади основания на высоту.
Для наклонной призмы существует и другой способ вычисления его объема.
Теорема
Объем наклонной призмы равен произведению бокового ребра на площадь перпендикулярного ему сечения.
Пример 1
Найдите объём наклонной призмы, основанием которой является параллелограмм ABCD. Сторона AB равна 3 см, сторона AD равна
5 см, ∠A=45°. Высота призмы равна 8 см.
Решение
Объём призмы равен произведению площади основания на высоту.
Площадь параллелограмма равна произведению смежных сторон на синус угла между ними.
Тогда
V=S·h=AB·AD·sinA·h=3·5·22·8=602 см3.
Ответ: 602 см3.
Пример 2
Дана треугольная призма ABCA1B1C1 (рис. 3). Найти ее объем, если AB=10 см, BC=10 см и AC=12 см, а боковое ребро AA1=8 см и составляет с плоскостью основания угол α=30°.
Решение
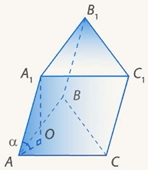
Рис. 3. Призма
Опустим перпендикуляр из точки A1 на плоскость ABC. Тогда A1O – высота призмы.
Рассмотрим прямоугольный треугольник AOA1. Катет A1O лежит напротив угла в 30°, значит, A1O=12AA1=4 см.
Площадь треугольника ABC найдем с помощью формулы Герона: S=pp-ap-bp-c где p=a+b+c2=10+10+122=16 см.
Тогда
V=S·h=pp-ap-bp-c·A1O=
=1616-1016-1016-12·4=192 см3.
Ответ: 192 см3.
Упражнение 1
1. Найти объём наклонной призмы, основанием которой является ромб АВСD. Сторона АВ=7 см, ∠A=30°. Высота призмы равна 10 см.
2. Дана треугольная призма ABCA1B1C1. Найти ее объем, если в основании лежит равносторонний треугольник со стороной 10, а боковое ребро AA1=14 и составляет с плоскостью основания угол α, равный 60°.
Контрольные вопросы
1. Как найти объём призмы?
2. Какой вид имеет призма, если высота совпадает с боковым ребром?
Ответы
Упражнение 1
1. 245 см3.
2. 525.
Предыдущий урок
Объём пирамиды
Объем
Следующий урок
Вычисление объёмов тел с помощью определённого интеграла
Объем
Введение
Вы уже знаете, как вычислять объемы некоторых тел, таких как куб, прямоугольный параллелепипед, прямая призма и цилиндр, в пространстве. Надо еще научиться вычислять объёмы наклонной призмы, конуса, шара пирамиды и других тел. Для этого попытаемся разбить искомое тело на уже известные нам фигуры, а их объёмы сложить.
Вычисление объема через определенный интеграл
Рассмотрим произвольную фигуру ![]() в пространстве, пусть это будет пирамида (на ее месте может быть любая другая фигура). Обозначим ее объем через
в пространстве, пусть это будет пирамида (на ее месте может быть любая другая фигура). Обозначим ее объем через ![]() – его нам и надо найти. Также будем считать, что тело
– его нам и надо найти. Также будем считать, что тело ![]() ограничено двумя параллельными плоскостями (одна совпадает с плоскостью основания, другая содержит вершину пирамиды). (См. Рис. 1.)
ограничено двумя параллельными плоскостями (одна совпадает с плоскостью основания, другая содержит вершину пирамиды). (См. Рис. 1.)

Рис. 1. Пирамида (фигура ![]() ) и две параллельные плоскости
) и две параллельные плоскости
Далее введем ось ![]() , перпендикулярную рассмотренным плоскостям, предположим, что координаты точек пересечения плоскостей и оси –
, перпендикулярную рассмотренным плоскостям, предположим, что координаты точек пересечения плоскостей и оси – ![]() и
и ![]() соответственно. (См. Рис. 2.)
соответственно. (См. Рис. 2.)

Рис. 2. Ось ![]() , пересекающая плоскости в точках
, пересекающая плоскости в точках ![]() и
и ![]()
Теперь разобьем отрезок ![]() на
на ![]() равных отрезков точками
равных отрезков точками ![]() и
и ![]() . (См. Рис. 3.)
. (См. Рис. 3.)

Рис. 3. Разбиение отрезка ![]() на
на ![]() равных отрезков
равных отрезков
Через каждую из этих точек проведем плоскость, перпендикулярную оси ![]() . (См. Рис. 4.)
. (См. Рис. 4.)

Рис. 4. Плоскости, перпендикулярные оси ![]()
Тогда тело ![]() разбилось на
разбилось на ![]() слоев, каждый из которых представляет из себя практически прямую призму (основание – не всегда многоугольник (если за тело
слоев, каждый из которых представляет из себя практически прямую призму (основание – не всегда многоугольник (если за тело ![]() взять конус или сферу, основанием будет круг), и верхнее основание не совсем равно нижнему). Значит, объем каждой части можно приближенно посчитать как объем прямой призмы, то есть как площадь основания, умноженную на высоту. (См. Рис. 5.)
взять конус или сферу, основанием будет круг), и верхнее основание не совсем равно нижнему). Значит, объем каждой части можно приближенно посчитать как объем прямой призмы, то есть как площадь основания, умноженную на высоту. (См. Рис. 5.)

Рис. 5. Разбиение пирамиды на слои
Через ![]() обозначим площадь сечения тела
обозначим площадь сечения тела ![]() плоскостью, проходящей через точку оси с абсциссой
плоскостью, проходящей через точку оси с абсциссой ![]() перпендикулярно этой оси.
перпендикулярно этой оси.
Тогда площадь слоя (прямой призмы) (см. Рис. 6) можно посчитать по формуле ![]() . То есть
. То есть ![]() . Учитывая, что
. Учитывая, что ![]() – постоянная величина, то ее можно вынести за знак суммы
– постоянная величина, то ее можно вынести за знак суммы ![]() .
.

Рис. 6. Слой пирамиды
Очевидно, что, увеличивая количество промежутков n и устремляя его к бесконечности, мы получим все более точное значение для объема. Тогда ![]() . Видим, что правая часть – это определенный интеграл функции
. Видим, что правая часть – это определенный интеграл функции ![]() на отрезке
на отрезке ![]() . В таком случае
. В таком случае ![]() .
.
Эта формула очень пригодится как на этом уроке, так и в дальнейшем, когда мы будем находить объемы пирамиды и конуса.
Объем наклонной призмы
Рассмотрим треугольную наклонную призму. Пусть дана треугольная наклонная призма ![]() и ось
и ось ![]() , перпендикулярная обоим основаниям призмы. (См. Рис. 7.)
, перпендикулярная обоим основаниям призмы. (См. Рис. 7.)

Рис. 7. Призма ![]() и ось
и ось ![]()
Докажем, что для произвольного ![]() на оси площадь перпендикулярного сечения
на оси площадь перпендикулярного сечения ![]() равна площади
равна площади ![]() основания призмы. Проведем сечение
основания призмы. Проведем сечение ![]() . Плоскости сечения и основания параллельны, так как они перпендикулярны одной прямой. (См. Рис. 8.)
. Плоскости сечения и основания параллельны, так как они перпендикулярны одной прямой. (См. Рис. 8.)

Рис. 8. Сечение ![]()
Значит, и прямые пересечения плоскостей с любой плоскостью параллельны. В частности, ![]() . Но тогда
. Но тогда ![]() – параллелограмм по определению, ведь боковые ребра призмы также параллельны (
– параллелограмм по определению, ведь боковые ребра призмы также параллельны (![]() ). (См. Рис. 9.)
). (См. Рис. 9.)

Рис. 9. ![]() – параллелограмм
– параллелограмм
А значит, ![]() . Аналогично
. Аналогично ![]() и
и ![]() . Значит,
. Значит, ![]() (по трем сторонам), а тогда их площади равны. (См. Рис. 10.)
(по трем сторонам), а тогда их площади равны. (См. Рис. 10.)

Рис. 10. ![]()
Отсюда следует, что ![]() для любого
для любого ![]() , где
, где ![]() – площадь произвольного сечения,
– площадь произвольного сечения, ![]() – площадь основания призмы. А значит, объем призмы равен (высоту примем за
– площадь основания призмы. А значит, объем призмы равен (высоту примем за ![]() ):
): ![]() .
.
Итак, объем треугольной наклонной призмы равен площади основания, умноженной на высоту ![]() .
.
Осталось заметить, что если разбить произвольную наклонную призму на треугольные (см. Рис. 11), то их высоты будут одинаковыми, а значит, объем исходной призмы можно вычислить так:
![]() .
.

Рис. 11. Разбиение многоугольной призмы на треугольные
Таким образом, формула ![]() верна для любой призмы. Что и требовалось доказать.
верна для любой призмы. Что и требовалось доказать.
Пример 1
Дана треугольная призма ![]() . Найти ее объем, если
. Найти ее объем, если ![]() см,
см, ![]() см и
см и ![]() см, а боковое ребро
см, а боковое ребро ![]() см и составляет с плоскостью основания угол
см и составляет с плоскостью основания угол ![]() . (См. Рис. 12.)
. (См. Рис. 12.)

Рис. 12. Иллюстрация к примеру 1
Решение. Найдем площадь основания призмы. Проведем высоту ![]() в равнобедренном треугольнике. Она будет и медианой. Отсюда получаем, что половина основания
в равнобедренном треугольнике. Она будет и медианой. Отсюда получаем, что половина основания ![]() см, а высота основания
см, а высота основания ![]() см (
см (![]() ), значит, площадь основания
), значит, площадь основания ![]() . (См. Рис. 13.)
. (См. Рис. 13.)

Рис. 13. Основание призмы
Далее, если ![]() – боковое ребро и
– боковое ребро и ![]() – высота, то
– высота, то ![]() прямоугольный, и по условию в нем
прямоугольный, и по условию в нем ![]() . Отсюда получается, что высота
. Отсюда получается, что высота ![]() см.
см.
Осталось подставить это в формулу для нахождения объема призмы ![]() .
.
Ответ: ![]() .
.
Теорема
Теорема.
Объем наклонной призмы равен произведению бокового ребра и площади сечения призмы, перпендикулярного боковой стороне
.
(См. Рис. 14.)

Рис. 14. Ребро призмы и перпендикулярное ему сечение
Обратите внимание: площадь сечения не равна площади основания. Она равна только в том случае, если призма прямая.
Другая формула нахождения объема наклонной призмы
Докажем, что объем наклонной призмы ![]() равен произведению бокового ребра
равен произведению бокового ребра ![]() на площадь перпендикулярного сечения
на площадь перпендикулярного сечения ![]() :
: ![]() . (См. Рис. 1.)
. (См. Рис. 1.)

Рис. 1. Иллюстрация к доказательству
Сначала вспомним, что ![]() (См. Рис. 2.)
(См. Рис. 2.)

Рис. 2. Высота, проведенная к основанию
Теперь рассмотрим точки ![]() и
и ![]() – точки пересечения прямых
– точки пересечения прямых ![]() и
и ![]() и прямых
и прямых ![]() и
и ![]() соответственно (прямые лежат в одинаковых гранях, так что можно их пересечь). Следует заметить, что плоскость
соответственно (прямые лежат в одинаковых гранях, так что можно их пересечь). Следует заметить, что плоскость ![]() – это то же самое, что и плоскость
– это то же самое, что и плоскость ![]() . (См. Рис. 3.)
. (См. Рис. 3.)

Рис. 3. Пересечение прямых ![]() и
и ![]() и прямых
и прямых ![]() и
и ![]()
Значит, угол между плоскостями ![]() и
и ![]() – это линейный угол
– это линейный угол ![]() двугранного угла. (См. Рис. 4.)
двугранного угла. (См. Рис. 4.)

Рис. 4. Линейный угол ![]() двугранного угла, образованного плоскостями
двугранного угла, образованного плоскостями ![]() и
и ![]()
По теореме площадь проекции некоторой фигуры равна произведению площади исходной фигуры на косинус угла между плоскостями, то есть ![]() .
.
Далее заметим, что ![]() , потому что плоскость
, потому что плоскость ![]() (т. к.
(т. к. ![]() и
и ![]() ) и
) и ![]() . И если рассмотреть высоту
. И если рассмотреть высоту ![]() треугольника
треугольника ![]() , то
, то ![]() (по построению) и
(по построению) и ![]() (т. к.
(т. к. ![]() ). Значит,
). Значит, ![]() и
и ![]() (
(![]() перпендикулярна двум пересекающимся прямым из основания), а тогда
перпендикулярна двум пересекающимся прямым из основания), а тогда ![]() , откуда
, откуда ![]() – высота.
– высота.
Теперь рассмотрим Рис. 5.

Рис. 5. Выносной рисунок
Из него видно, что ![]() . Тогда
. Тогда ![]()
Имеем, что ![]() и
и ![]() . Значит,
. Значит, ![]() . Что и требовалось доказать.
. Что и требовалось доказать.
Пример 2
Найти объем наклонной треугольной призмы ![]() , если расстояния между ее боковыми ребрами
, если расстояния между ее боковыми ребрами ![]() ;
; ![]() ;
; ![]() , а площадь боковой поверхности
, а площадь боковой поверхности ![]() . (См. Рис. 15.)
. (См. Рис. 15.)

Рис. 15. Иллюстрация к примеру 2
Решение. Площадь боковой поверхности равна сумме площадей боковых граней. Каждая грань представляет собой параллелограмм, причем у этих параллелограммов есть сторона ![]() (все боковые стороны призмы равны), а высота каждого параллелограмма – это высота между боковыми ребрами. (См. Рис. 16.)
(все боковые стороны призмы равны), а высота каждого параллелограмма – это высота между боковыми ребрами. (См. Рис. 16.)

Рис. 16. ![]() – боковое ребро призмы
– боковое ребро призмы
Тогда ![]() . Значит, боковое ребро призмы
. Значит, боковое ребро призмы ![]() .
.
Теперь заметим, что перпендикулярное сечение – треугольник со сторонами ![]() ,
, ![]() и
и ![]() . Действительно, если рассмотреть перпендикуляры
. Действительно, если рассмотреть перпендикуляры ![]() и
и ![]() к боковому ребру
к боковому ребру ![]() , равные
, равные ![]() и
и ![]() , то плоскость
, то плоскость ![]() , содержащая их, будет перпендикулярна боковому ребру
, содержащая их, будет перпендикулярна боковому ребру ![]() , а тогда она перпендикулярна и оставшимся двум боковым ребрам
, а тогда она перпендикулярна и оставшимся двум боковым ребрам ![]() и
и![]() , т.к.
, т.к. ![]() , а значит, оставшаяся сторона сечения
, а значит, оставшаяся сторона сечения ![]() (См. Рис. 17.)
(См. Рис. 17.)

Рис. 17. Перпендикулярное сечение – треугольник со сторонами 13, 30 и 37
Найдем площадь этого треугольника по формуле Герона. Полупериметр ![]() , значит
, значит
![]() .
.
Окончательно, ![]() .
.
Ответ:![]() .
.
Заключение
На этом уроке мы выяснили, как находить объем фигуры через определенный интеграл ![]() , и с помощью него была выведена формула для нахождения объема произвольной призмы (в дальнейшем выведем формулы для объема пирамиды, конуса и шара). Кроме того, мы познакомились с еще одной формулой для вычисления объема наклонной призмы
, и с помощью него была выведена формула для нахождения объема произвольной призмы (в дальнейшем выведем формулы для объема пирамиды, конуса и шара). Кроме того, мы познакомились с еще одной формулой для вычисления объема наклонной призмы ![]() И решили несколько задач на использование этих формул.
И решили несколько задач на использование этих формул.
Список литературы
1. Геометрия. Учебник для 10-11 классов. Атанасян Л.С. и др. 18-е изд. – М.: Просвещение, 2009. – 255 с.
2. А.В. Погорелов. Геометрия 11 класс. – М.: Просвещение, 2002.
3. Бутузов В.Ф., Глазков Ю.А., Юдина И.И. Геометрия. 11 класс. Рабочая тетрадь. 8-е изд. – М.: Просвещение, 2013. – 78 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-сайт «ЯКласс» (Источник)
2. Интернет-сайт 900igr.net (Источник)
3. Интернет-сайт obmir.ru (Источник)
Домашнее задание
1. Основанием наклонной призмы является равнобедренный треугольник с боковой стороной ![]() см и углом при вершине
см и углом при вершине ![]() . Боковое ребро призмы равно
. Боковое ребро призмы равно ![]() см и образует с плоскостью основания угол
см и образует с плоскостью основания угол ![]() . Найдите объем призмы.
. Найдите объем призмы.
2. Все грани призмы – равные ромбы со стороной ![]() см и острым углом
см и острым углом ![]() . Найдите объем призмы.
. Найдите объем призмы.
3. Боковое ребро наклонной треугольной призмы равно ![]() и удалено от противоположной боковой грани на расстояние
и удалено от противоположной боковой грани на расстояние ![]() . Расстояние между двумя другими боковыми ребрами равно
. Расстояние между двумя другими боковыми ребрами равно ![]() . Найдите объем призмы.
. Найдите объем призмы.
Умение определять объем пространственных фигур является важным для решения геометрических и практических задач. Одной из таких фигур является призма. Рассмотрим в статье, что она собой представляет, и покажем, как вычислять объем наклонной призмы.
Что понимают под призмой в геометрии?
Речь идет о правильном полиэдре (многограннике), который образован двумя одинаковыми основаниями, находящимися в параллельных плоскостях, и несколькими параллелограммами, соединяющими отмеченные основания.
Основаниями призмы могут быть произвольные многоугольники, например, треугольник, четырехугольник, семиугольник и так далее. Причем число углов (сторон) многоугольника определяет название фигуры.
Любая призма, имеющая в основании n-угольник (n – число сторон), состоит из n+2 граней, 2 × n вершин и 3 × n ребер. Из приведенных чисел видно, что количества элементов призмы соответствуют теореме Эйлера:
3 × n = 2 × n + n + 2 – 2
Ниже рисунок показывает, как выглядят треугольные и четырехугольные призмы, сделанные из стекла.

Виды фигуры. Наклонная призма
Выше уже было сказано, что название призмы определяется числом сторон многоугольника в основании. Однако существуют и другие особенности в ее строении, определяющие свойства фигуры. Так, если все параллелограммы, образующие боковую поверхность призмы, представлены прямоугольниками или квадратами, то такая фигура называется прямой. Для прямой призмы расстояние между основаниями равно длине бокового ребра любого прямоугольника.
Если же некоторые или все боковые стороны являются параллелограммами, то речь идет о наклонной призме. Высота ее уже будет меньше, чем длина бокового ребра.
Еще один критерий, по которому проводят классификацию рассматриваемых фигур — это длины сторон и углы многоугольника в основании. Если они равны друг другу, то многоугольник будет правильным. Прямая фигура с правильным многоугольником в основаниях называется правильной. С ней удобно работать при определении площади поверхности и объема. Наклонная призма в этом плане представляет некоторые трудности.
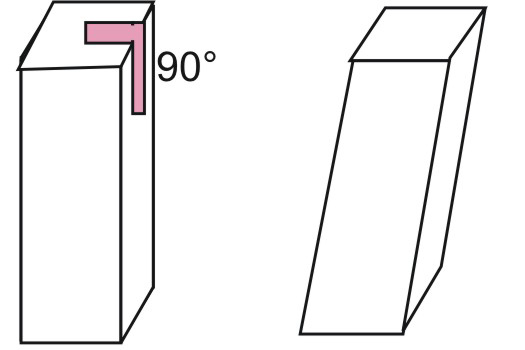
На приведенном рисунке показаны две призмы, имеющие четырехугольное основание. Угол 90° показывает принципиальную разницу между прямой и наклонной призмой.
Формула для определения объема фигуры
Часть пространства, ограниченная гранями призмы, называется ее объемом. Для рассматриваемых фигур любого типа эту величину можно определить по следующей формуле:
V = h × So
Здесь символом h обозначена высота призмы, которая является мерой дистанции между двумя основаниями. Символ So – одного основания площадь.
Площадь основания найти несложно. Учитывая тот факт, является правильным многоугольник или нет, а также зная количество его сторон, следует применить соответствующую формулу и получить So. Например, для правильного n-угольника с длиной стороны a площадь будет равна:
Sn = n / 4 × a2 × ctg (pi / n)
Теперь перейдем к высоте h. Для прямой призмы определение высоты не представляет никаких трудностей, однако для призмы наклонной – это непростая задача. Решать ее можно различными геометрическими методами, отталкиваясь от конкретных начальных условий. Тем не менее существует универсальный способ определения высоты фигуры. Опишем его кратко.
Идея заключается в нахождении расстояния от точки в пространстве до плоскости. Предположим, что плоскость задана уравнением:
A × x+ B × y + C × z + D = 0
Тогда от точки с координатами (x1; y1; z1) плоскость будет находиться на расстоянии:
h = |A × x1 + B × y1 + C × z1 + D| / √ (A2 + B2 + C2)
Если координатные оси расположить так, что точка (0; 0; 0) будет лежать в плоскости нижнего основания призмы, тогда уравнение для плоскости основания можно записать так:
z = 0
Это означает, что формула для высоты запишется так:
h = z1
Достаточно найти координату z любой точки верхнего основания, чтобы определить высоту фигуры.
Пример решения задачи
На рисунке ниже дана четырехугольная призма. Основанием наклонной призмы является квадрат со стороной 10 см. Необходимо вычислить ее объем, если известно, что длина бокового ребра равна 15 см, а острый угол фронтального параллелограмма равен 70°.

Поскольку высота h фигуры также является высотой параллелограмма, то используем формулы для определения его площади, чтобы найти h. Обозначим стороны параллелограмма так:
a = 10 см;
b = 15 см
Тогда можно записать для него следующие формулы для определения площади Sp:
Sp = a × b × sin (α);
Sp = a × h
Откуда получаем:
h = b × sin (α)
Здесь α – острый угол параллелограмма. Поскольку основанием является квадрат, то формула объема наклонной призмы примет вид:
V = a2 × b × sin (α)
Подставляем из условия данные в формулу и получаем ответ: V ≈ 1410 см3.
