Как найти объем образца материала

Как найти объем образца материала

ЛЕКЦИЯ
11

Тема:
Определение объемной массы.

План

1       
Определение объемной массы образца
правильной геометрической формы.

2       
Определение объемной массы образца
неправильной геометрической формы.

      
Объемной массой тела принято называть отношение массы тела m
к занимаемому этим телом объему V вместе
с трещинами и порами (г/см3, кг/м3),

                                 
Y0=m/V

      
Объемная масса может совпадать с плотностью или быть близкой к ней лишь тогда,
когда тело будет абсолютно плотным, без газовых включений и пор (стекло, сталь
и т. д.).

      
Массу образца определяют взвешиванием на весах соответствующей степени точности.
Объем образца определяют в зависимости от его формы и пористости различными
способами.

       1.
Объем образцов правильной геометрической формы, представляющих собой куб,
параллелепипед и др. можно определить измерением и вычислить по известным геометрическим
формулам. Для прямого параллелепипеда V=S/h,
для куба V=h3
и т.д. Линейные измерения производят штангенциркулем. Если образец имеет форму
параллелепипеда или куба, то производят по три измерения: длины, ширины,
высоты, причем каждую грань измеряют в трех местах и находят среднее значение.
Перемножив средние значения высоты, длины и ширины, вычисляют объем образца.

       У образцов,
имеющих цилиндрическую форму на двух параллельных основаниях, проводят по два
взаимно перпендикулярных диаметра и измеряют их величину. Одновременно измеряют
диаметр по середине цилиндра. Высоту образца измеряют в точках пересечения
диаметров с окружностью. Величину диаметра берут как среднее из пяти замеров, а
значение высоты – как среднее из четырех измерений. Объем параллелепипеда и
цилиндра находят по приведенным выше формулам.

       2.Если
испытуемый материал не имеет правильной геометрической формы, из него вырезают
или выпиливают кубики размером 50х50х50 мм, а из пористых материалов – кубики
размером 70х70х70 мм и измеряют, как указано выше.

        Если
тело не имеет правильной геометрической формы, то объемную массу его находят гидростатическим
взвешиванием в инертной по отношению к нему жидкости или по объему вытесненной
им жидкости при погружении в нее. Вес тела определяют обычным взвешиванием.

                              
Контрольные вопросы

1.     Что
называется объемной массой тела?

2.    
Как определить объемную массу образца
правильной геометрической формы?

3.    
Как определить объемную массу образца
неправильной геометрической формы?

                                 
Литература

1. Клюковский Г.
И., Ульянова Г. Г. Лабораторный практикум по общей технологии строительных
материалов. М.: Высшая школа, 1982, с. 20-26.

Источник

Объем – образец

Cтраница 1

Объем образца, принимающий участие в колебаниях, определяется двумя фиксированными точками, показанными на рисунке. Комбинация светоизлучаю-щего диода и фототранзистора является приемником автоколебаний вибратора. Обратная связь с возбуждающей катушкой осуществляется через усилитель. Вибратор помещен в запаянный стеклянный резервуар с двойной оболочкой, заполненной тешюпроводящим газом. Температура вибратора поддерживается постоянной путем циркуляции термостатированной жидкости в оболочке резервуара. Датчиком температуры служит терморегулятор, помещенный между ветвями V-образной трубки. С целью компенсации влияния температуры на показания денсиметра авторами [67] использована конструкция с двумя осцилляторами. Экспериментально было установлено, что погрешность при определении плотности в этом случае снижается с 6 – 10 до 0 3 – 10 г см-3.
 [2]

Объем образца в такой ампуле ( чаще всего изготавливаемой из стекла), как правило, равен 0 03 – 0 05 мл, тогда как для обычных цилиндрических ампул этот объем равен примерно 0 4 мл. Некоторые ампулы имеются в продаже, но их очень трудно промывать.
 [4]

Объем образца определяют как разность между уровнем песка с образцом в приборе и первоначальным уровнем песка в приборе без образца.
 [5]

Объем образца определяют по количеству вытесненной им воды или по потере в весе образца, взвешенного в воде. Потом взвешивают образец, насыщенный водой ( Pz), который предварительно насухо обтирают.
 [6]

Объем образцов не должен превышать 50 % всего объема воздуха в эксикаторе над соответствующим раствором. Испытания проводят при постоянной температуре окружающего воздуха 20 2 С.
 [8]

Объем образца в м3 определяют умножением длины на ширину и толщину образца в метрах. Объем образцов теплоизоляционных материалов изделий в зависимости от их вида устанавливают одним из следующих методов. Объем жестких и гибких теплоизоляционных изделий определяют на основании линейных размеров.
 [9]

Объем образца определяют как среднее из ряда измерений. Образец взвешивают сперва в сухом виде и затем пропитанным водой.
 [10]

Объем образца для анализа и точность определения находятся в прямой зависимости.
 [11]

Объем образца определяют путем гидростатического взвешивания.
 [12]

Объем образца также определяют по его размерам, если наделить его правильной геометрической формой, а объем пор – по методу взвешивания.
 [13]

Объем образца для однократного разделения достигает 20 мл.
 [14]

Объем образца ( монолита) непористой скальной породы находится самым простым способом – путем погружения образца в воду и замера вытесненного при этом объема воды. С равным успехом при этом определении может быть использован известный – физический принцип измерения объема тела по потере его веса при погружении в воду за счет веса вытесненной при этом воды.
 [15]

Страницы:  

   1

   2

   3

   4

   5

Источник

Любые физические показатели можно измерить опытным путем и рассчитать производные от них. Например, измерив объем и массу, мы можем найти плотность — производную от них величину, или зная высоту поверхности и вес вещи можем рассчитать энергию.

Эксперименты по определению и изучению основных физических показателей помогут наглядно продемонстрировать и понять суть физических законов, которые действуют в нашем мире.

С помощью практических опытов ученики смогут легче запомнить формулы, разобраться с теоремами, уверенно объяснять физические явления, а также ответить на вопрос, какими экспериментами в физике можно это подтвердить. Например, изучить плавучесть, земное притяжение или доказать взаимосвязь массы и энергии.

Формула зависимости массы от объема и плотности

Для того, чтобы найти плотность жидкости или твердого вещества, существует базовая формула: плотность равна массе, поделенной на объем.

Записывается это так:

И из нее можно вывести еще две формулы.

Формулу для объема тела:

А также формулу для расчета массы:

Как видите, запомнить последнюю очень легко: это единственная формула, где две единицы нужно умножить.

Для запоминания этой зависимости можно использовать рисунок в виде «пирамидки», разделенной на три секции, в вершине которой находится масса, а в нижних углах – плотность и объем.

Несколько иначе обстоят дела с газами.

Рассчитать их вес гораздо сложнее, так как у газов нет постоянной плотности: они рассеиваются и занимают весь доступный им объем.

Для этого пригодится понятие молярной массы, которую можно найти, сложив массу всех атомов в формуле вещества при помощи данных из периодической таблицы.

Вторая единица, которая нам понадобится – количество вещества в молях. Его можно вычислить по уравнению реакции. Подробнее об этом можно узнать в рамках курса химии.

Другой способ нахождения мольного количества – через объем газа, который нужно поделить на 22,4 литра. Последнее число – это объемная постоянная, которую стоит запомнить.

В итоге, зная две предыдущие величины, мы можем определить массу газа:

где M – это молярная масса, а n – количество вещества.

Результат получится в граммах, поэтому для решения физических задач важно не забыть перевести его в килограммы, поделив на 1000. Числа в этой формуле часто могут оказываться достаточно сложными, поэтому для вычислений может понадобиться калькулятор.

Еще один нестандартный случай, с которым можно столкнуться – необходимость найти плотность раствора

. Для этого существует формула средней плотности, построенная аналогично формулам других средних величин.

Для двух веществ посчитать ее можно так:

Также из этой формулы можно вывести несколько других в зависимости от того, какие из величин известны по условию задачи.

Проект: «Объём и вытеснение воды»

В ходе эксперимента установим, как объем вытесненной воды зависит от объема погруженной вещи.

Впервые соответствие объема воды, вытесненной объектом, и объема этого объекта установил Архимед, когда опустился в ванную и крикнул «Эврика!». В проекте мы наглядно покажем объем вымещения воды, а затем попробуем спрогнозировать результат.

Что нам понадобится:

  • три стакана, два из которых полностью одинаковые;
  • вода;
  • карандаш;
  • монеты;
  • камни, по размеру крупнее монет;
  • другие предметы для погружения в стакан;
  • емкость для контроля объема вылитой воды.

Ход эксперимента:

  1. Возьмем одинаковые стаканы, которые не полностью, но одинаково наполним водой.
  2. Отметим уровень воды в обоих стаканах.
  3. Поочередно бросим сначала монету в один стакан, а потом камень во второй стакан. Что стало с уровнем воды?
  4. Бросим по 10 монет и камней в каждый стакан. Что произошло с уровнем воды?
  5. Бросаем монеты и камни до тех пор, пока вода не выливается через край стаканов. Сколько поместилось монет, а сколько камней, пока вода не стала вытекать?
  6. Возьмем третий стакан, также наполним его водой.
  7. Попробуем угадать, сколько монет или камней поместиться в стакан, прежде чем вода начнет вытекать? Проверяем на практике.
  8. Проделаем такой же опыт со стаканами других параметров, а также иными объектами.
  9. Предположим, сколько монет или камней нужно будет бросить в стакан, чтобы уровень воды стал таким же, как у стакана с другими объектами. Сравним их объем.

Вывод:

Погружая в воду различные объекты, по объему вытесненной жидкости мы смогли установить их объем, тем самым проверив закон Архимеда на практике.

Архимед установил, что объект, опущенный в воду, вытесняет такой объём жидкости, который равен объёму самого объекта. Соответственно, если объектов несколько (10 монет или камней), то объем вытекшей жидкости будет равен совокупному объему всех помещенных в воду объектов.

Таблица плотности некоторых веществ

Плотность многих веществ известна заранее и легко находится по соответствующей таблице.

В работе с ней важно обращать внимание на размерности и не забывать о том, что все данные собраны при нормальных условиях: комнатной температуре в 20 градусов Цельсия, а также определенном давлении, влажности воздуха и так далее.

Плотности других, более редких веществ можно найти онлайн.

Как минимум одно из значений плотности стоит запомнить, так как оно часто появляется в задачах. Это плотность воды – 1000 кг/м3 или 1 г/см3.

Как пользоваться калькулятором плотности:

Следуйте данным инструкциям по расчету с помощью этого онлайн-инструмента. С помощью этого калькулятора вы можете производить расчеты в простом и продвинутом режимах. Давайте взглянем!

Входы:

  • Прежде всего, выберите во вкладке то, что вам нужно найти.
  • Затем введите значения во все обозначенные поля в соответствии с выбранной опцией.
  • Наконец, нажмите кнопку “Рассчитать”.

Выходы:

Как только вы заполните все поля, калькулятор покажет:

  • Плотность объекта
  • Масса объекта
  • Объем объекта
  • Корень кубический из объема

Заметка:

Есть дополнительное поле, где вы можете ввести категорию материала и название материала, этот калькулятор найдет плотность выбранного материала. Если вы не знаете значение объема, используйте предварительный вариант этого калькулятора для расчета объема, в противном случае используйте простой режим.

Расчет плотности тела и формулы расчета массы и объема тела по плотности

Окружающий мир состоит из множества различных веществ. Так, например, лавочка в парке или баня за городом сделаны из дерева, платформа утюга и сковорода сделаны из металла, покрышка на колесе и ластик на карандаше сделаны из резины. Различные предметы имеют различный вес — любой человек без труда донесёт с рынка сочный спелый арбуз, а вот гирю такого же размера вряд ли удастся оторвать от земли.

Всем известная знаменитая шутка: «Что тяжелее — килограмм ваты или килограмм гвоздей?» очень точно характеризует понятие плотности тела. Почему разные предметы, имея одинаковый объём, различаются по весу? Потому что они состоят из различных веществ и имеют разную плотность. В системе измерений данную величину принято измерять в кг/м³, но также возможно использование и других единиц: кг/л, г/см³.

Видео о плотности тела

Какие факторы влияют на плотность тела?

Плотность одних и тех же тел зависит от давления и температуры. Как правило, при высоком давлении молекулы утрамбованы плотнее, и, соответственно, вещество имеет бо́льшую плотность. Обычно при повышении температуры расстояние между молекулами увеличивается, что приводит к уменьшению плотности. Бывают случаи, когда такая зависимость имеет обратное значение. Так, например, плотность воды меньше плотности льда, несмотря на то что лёд имеет более низкую температуру. Причина такого явления — молекулярная структура льда. Часто вещество, переходя из жидкого в твёрдое состояние, изменяет свою молекулярную структуру таким образом, что расстояние между молекулами сокращается, и, соответственно, плотность становится больше. Когда образуется лёд, расстояние между молекулами и их объём становятся больше, а плотность — меньше. Поэтому в зимнее время, если забыть слить с труб воду, она замёрзнет, в результате чего труба разорвётся.

На плотность воды влияют и примеси, которые в ней находятся. Так, например, у морской воды плотность больше, чем у пресной. Если налить в сосуд солёную воду, а сверху — пресную, то последняя будет «плавать» на поверхности морской воды. Поскольку визуально данное явление увидеть сложно, то для эксперимента можно заполнить резиновый шар пресной водой и поместить его в солёную. Шар будет плавать на её поверхности. Можно сказать, что человеческое тело также представляет собой оболочку, наполненную пресной водой, поскольку, как известно, оно состоит из воды примерно на 50-75%. Поэтому держаться на поверхности солёной воды гораздо легче, чем пресной. И чем больше концентрация соли в воде, тем более она плотная.

Как рассчитать плотность тела?

Расчет плотности тела производится по следующей формуле:

К примеру, вода имеет плотность 1000 кг/м³, а лёд — 900 кг/м³. Поскольку лёд имеет меньшую массу по сравнению с водой, то зимой на водоёме он всегда находится на поверхности воды. В данном случае можно определить, что, если плотность льда равняется 900 кг/м³, значит, ледяной куб со стороной 1 м будет весить 900 кг.

Для того чтобы рассчитать плотность, необходимо знать его объём и массу. Это значит, что вещество можно взвесить, измерить, и на основании полученных данных вычислить плотность по формуле. Поскольку плотность измеряется в кг/л или в г/см³, то иногда приходится пересчитывать одни величины в другие. Делается это очень просто:

  • 1 грамм = 0,001 кг, а 1 см³ = 0,000001 м³, и соответственно:
  • 1 г/(см)^3 =1000кг/м^3

Иногда необходимо рассчитать плотность газообразного вещества. Для этого используется та же формула для расчета плотности тела, но несколько в другом виде:

где М — молярная масса газа, Vm— молярный объём (равен приблизительно 22,4 л/моль).

Масса всех тел всегда зависит не только от их размеров, но и от веществ, из которых они состоят. Так, тела, имеющие одинаковый объём, но состоящие из различных веществ, будут отличаться друг от друга своими массами. И наоборот, если у тел массы одинаковы, но состоят они из разных веществ, то их объёмы также будут отличаться. Например:

  • Куб из железа с рёбрами по 10 см весит 7,8 кг.
  • Куб из алюминия такого же размера весит 2,7 кг.
  • Ледяной куб с аналогичными размерами весит 0,9 кг

Расчет массы тела и объёма по плотности

Часто возникает необходимость рассчитать массу или объём тела. При этом следует знать, что каждое тело имеет постоянную определённую плотность. К примеру, вода имеет плотность 1000 кг/м³, этиловый спирт — 800 кг/м³.

Поскольку величины постоянные, то для каждого вещества существуют специальные таблицы, которыми пользуются при расчетах.

Исходя из основной формулы определения плотности тела, можно легко рассчитать и его объём или массу:

Для примера можно решить простые задачи:

Необходимо определить массу детали, выполненной из стали, если известно, что её объём составляет 120 см³.

Для того чтобы вычислить массу, требуется знать объём и плотность вещества. По условию задачи объём известен, а плотность необходимо найти по таблице (плотность стали = 7,8 г/см³). Тогда расчет массы тела по его плотности и объёму будет иметь следующий вид:

Требуется рассчитать объём бутылки подсолнечного масла, если известно, что её масса составляет 930 г.

Для того чтобы определить объём, необходимо знать массу и плотность. Масса известна, а плотность нужно найти по таблице (плотность подсолнечного масла = 0.93 г/см³). Тогда:

Расчет массы и объёма тела по плотности выполняется при помощи следующих таблиц:

Плотность воды

  • Если плотность вещества больше, чем плотность воды, то оно будет полностью погружаться в воду. И наоборот, предметы, сделанные из материала, плотность которого ниже плотности воды, будут плавать на её поверхности. Примером данного правила является лёд, плотность которого меньше плотности воды. Поэтому кусочек льда, брошенный в воду или другой напиток, сделанный из воды, всплывёт на поверхность.
  • В практической жизни эти свойства веществ часто используются человеком. К примеру, конструируя корпуса судов, инженеры используют материалы, плотность которых выше, чем плотность воды. Поскольку таким материалам свойственно тонуть в воде, то в корпусах суден необходимо создавать полости с воздухом — ведь его плотность значительно ниже плотности воды.
  • В другом примере, когда требуется, чтобы предмет погружался в воду, необходимо выбирать материалы с плотностью выше, чем плотность воды. К примеру, чтобы лёгкая наживка для рыб во время рыбалки погрузилась в воду на достаточную глубину, рыболов привязывает к леске грузило, сделанное из материала высокой плотности. Обычно в качестве грузила используется свинец.
  • Плотность масла, жира, нефти меньше, чем плотность воды, поэтому, если их пролить в воду, они будут плавать на её поверхности. Это свойство очень помогает в ситуациях, когда в морях или океанах при транспортировке нефти она проливается в воду. Благодаря тому, что пролитая нефть не смешивается с водой и плавает на её поверхности, уже было предотвращено множество экологических катастроф, поскольку вода была быстро очищена от вредного для природы вещества.
  • В кулинарии свойство жира всплывать на поверхность воды помогает эффективно удалять его излишки из ёмкости с блюдом. В супе, охлаждённом в холодильнике, жир застывает, что позволяет очень легко удалить его с поверхности. Это свойство жира помогает уменьшить количество калорий и холестерина в еде.
  • Правило о плотности жидких веществ хорошо известно профессиональным барменам. При приготовлении многослойных коктейлей используются жидкости с разными плотностями. Для этого жидкость, обладающую меньшей плотностью, необходимо аккуратно налить на более плотную жидкость.
  • Иногда низкая плотность жира может, наоборот, мешать. Так, например, в процессе приготовления холодных десертов или фруктовых коктейлей жирные продукты очень трудно смешивать с водой, на поверхности которой может образоваться отдельный слой из жира, ухудшив при этом внешний вид и вкус блюда.

Видео о расчете массы и объема тела по плотности

Метод вытеснения жидкости

Как уже известно, для определения плотности тела необходимо знать две величины — объём и массу. Если масса легко определяется с помощью обычных весов, то как посчитать плотность тела, если неизвестен его объём, может показаться довольно сложной задачей.

Но для определения объёма тела также существует очень простой метод, изобретённый Архимедом:

  • Необходимо налить воду в мерный стакан и зафиксировать количество налитой воды.
  • Затем следует полностью погрузить в эту воду предмет, объём которого требуется определить.
  • Из количества воды, которая находилась в сосуде изначально, до погружения в неё тела, необходимо вычесть то количество воды, которое осталось после его погружения.

Конечно, такой метод нельзя использовать для вычисления объёма фотоаппарата или других предметов, которые испортятся от контакта с водой. Следует помнить, что данный метод не будет работать при погружении в воду тел, которые склонны её поглощать (например, плюшевый медвежонок).

В какой сфере жизни Вам пригодились знания о плотности тела? Расскажите об этом в комментариях.

Источник: www.rutvet.ru

Проект: «Масса или вес»

Масса и вес – это синонимы или есть различия? Выполнив настоящий проект, мы опытным путем узнаем отличие веса тела от массы.

Масса – это количество материи, содержащейся в объекте, тогда как вес – это сила притяжения, которая воздействует на объект.

Масса предмета или человека не изменяется при перемещении в пространстве. Что нельзя сказать о весе, который напрямую зависит от силы гравитации. Поэтому на Луне, где сила притяжения меньше чем на Земле, предметы всегда будут весить меньше.

В свою очередь сила гравитации зависит от массы. Чем выше масса предмета, тем выше показатель силы притяжения.

Научный проект способствует приобщению учеников к исследованиям, изучению массы, использованию контрольной точки, установлению зависимых и независимых переменных, сбору данных. Ученики составляют презентации, учатся принимать решения на основании полученных опытным путем данных. Дети смогут почувствовать себя настоящими учеными.

Что нам понадобится:

  • канцелярские ножницы;
  • степлер;
  • маркер;
  • весы;
  • губка;
  • водяной шарик;
  • фрукт;
  • камень;
  • пачка попкорна.

Ход эксперимента:

  1. Подготовим все материалы, необходимые для проведения опыта. По желанию, для фотоотчета, можно взять фотоаппарат. Сделаем по две копии ниже представленных таблиц.
  2. Выбираем себе человека в пару, который, не зная ваши результаты, повторит все шаги, а потом оформим наблюдения таблицей.
  3. Определяем приблизительный вес каждого выбранного нами предмета по собственным ощущениям. Раскладываем все предметы по убыванию веса: от самого тяжелого до самого легкого.
  4. Пронумеруем расставленные предметы. Самый легкий – номер 1 и т.д.
  5. Теперь можно приступить к самому эксперименту – взвешиваем каждый предмет на весах по отдельности.
  6. Сверяем полученные результаты с записанными ранее. На сколько совпал вес? Как вы оценивали вес предмета без измерительного прибора? Возможно, вас смутил размер предмета?
  7. Все шаги, начиная с 4 пункта, заканчивая 7 пунктом, повторяет партнер.
  8. Сравниваем данные, записанные в вашей таблице, с результатами партнера. Все совпало? Вами допущены одинаковые ошибки? На каком этапе?
  9. Проанализируем полученные результаты. К какому выводу вы пришли? Опишите проект с использованием установленных данных, а также списка использованной литературы.

Таблица с упорядоченными по собственным ощущениям предметами: от более тяжелого объекта

Моя последовательность
Последовательность моего партнёра

Таблица с упорядоченными предметами на основании измерений весами

Объекты Настоящий вес
пачка попкорна
фрукт
камень
ножницы
фломастер
губка
шарик с водой
степлер
денежная купюра
монета

Вывод:

Как определяется масса воды в опыте? В ходе проекта мы установили, что массу тела можно измерить с помощью весов. Как вы думаете, на что влияет масса и вес предмета? Как с помощью массы рассчитать вес?

Зная массу можно рассчитать силу притяжения, то есть вес тела. Получается, что вес напрямую зависит от массы тела. Поскольку масса Луны меньше Земли, то вес объектов на этом небесном теле будет меньше. Луна гораздо слабее притягивает к себе предметы, чем Земля. Значение силы земного притяжения трудно переоценить, ведь она помогает нам сохранять равновесие и не падать при ходьбе.

Калькулятор массы

Для различных изделий сложной формы и профиля, с наличием прорезей и отверстий очень трудно рассчитать вес, а это очень важный момент – для транспортировки, для расчета монтажных параметров, для конструкторской документации и других целей. Процесс взвешивания также представляет собой сложности, особенно, когда изделия крупногабаритные – например, трубы, валы, турбины, металлические или деревянные конструкции, изделия из бетона и железобетона и т.д., или же вес небольшой детали, но сложной конфигурации.

Проект: «Работа и энергия»

Выполнив проект, мы узнаем, что такое энергия и работа, как их измерить, как наклонная поверхность, вес объекта влияют на расстояние, до которого скатиться предмет.

Чтобы понять, что такое энергия, в ходе эксперимента будем изменять угол наклона поверхности и вес объекта.

Для того чтобы рассчитать энергию воспользуемся формулой: E = HxW, где E – энергия, H – высота, а W – вес.

Единицы измерения энергии — граммы на сантиметры: в граммах измеряем вес выбранной вещи, сантиметрах — высоту.

В качестве предмета удобно взять банку, вес которой можно регулировать, наполняя водой. Что даст совершенно разные результаты, поскольку при плескании воды в банке часть энергии теряется.

Что нам понадобится:

  • гладкая, ровная доска, шириной минимум 30 см, длиной около 120 см;
  • две банки (одну большего размера, другую меньшего) цилиндрической формы с крышкой и широким горлышком. Например, банки из-под томатной пасты, майонеза, чипсов и т.д.;
  • вода;
  • карандаш;
  • книги, учебники или другие вещи для подпорки доски;
  • фотоаппарат;
  • скотч.

Ход эксперимента:

  1. С использованием книг устанавливаем доску под наклоном так, чтобы расстояние от поднятой стороны до поверхности было 8 см. В этом месте начертим линию на доске.
  2. Приклеиваем скотч по длине доски, для того чтобы потом быть уверенными, что банка катиться по прямой.
  3. Десять раз скатываем большую банку по доске, начиная от размеченной линии. После каждого скатывания измеряем расстояние от нижнего края доски до места остановки банки. Подсчитываем средний результат.
  4. Увеличиваем угол наклона доски, подложив под нее еще одну книгу. Находим участок на доске, расстояние от которого до поверхности 8 см, чертим на этом месте линию. Далее повторяем действия из пункта 3. Изменились ли результаты? Что будет, если скатывать банку не с отмеченной линии, а выше или ниже?
  5. Теперь повторяем шаги 2-4 с маленькой банкой. Есть ли разница между полученными результатами, если рассчитывать энергию по вышеописанной формуле.

Для сравнения повторим шаги 2-4 для большой банки, наполненной водой. Как объяснить полученные результаты?

Вывод:

Результаты проекта показали, что неважно, на каком расстоянии над поверхностью земли мы начинаем скатывать предмет, независимо от угла наклона банка всегда останавливалась на одном расстоянии от конца доски. Как вы думаете, почему так происходит и, причем здесь энергия?

Такие результаты легко объяснимы, если рассчитать количество энергии, которое необходимо для скатывания банки. Расстояние, на которое прокатиться банка напрямую зависит от энергии, которой она будет обладать, когда докатиться до нижнего края доски.

Проделанный опыт подтверждает, что энергия у банки становится больше, если увеличиваются наклон доски или вес банки за счет наполнения ее водой.

За счет изменения энергии совершается работа всех внутренних и внешних сил, действующих на банку с разной мощностью.

Но, узнать точную массу таких изделий можно гораздо проще на нашем сайте

Мы предлагаем Вашему вниманию универсальный интерактивный калькулятор массы для самостоятельного расчета массы изделий самой разной формы из материалов цилиндрической или листовой формы. Его особенность в том, что он позволяет узнать вес детали или изделия не только из металлопроката и сплавов, но и любых других материалов: дерева и МДФ, пластиков и полимеров, бумаги, картона, резины, бетона, кирпича. Сделать это можно просто внеся габаритные показатели детали с вычетом размеров отверстий и прорезей, а также, величину коэффициента плотности материала, из которого деталь изготовлена. Точные данные можно найти в представленной рядом таблице.

Диаметр Длина Плотность
мм мм кг/мм 3
Масса общая
кг
Длина Ширина Толщина Плотность
мм мм мм кг/мм 3
Масса общая
кг
Длина Ширина Количество
мм мм шт

Масса цилиндрической детали рассчитывается следующим образом:

• В соответствующие поля калькулятора массы внести размерные показатели: диаметр, длину и справочную плотность материала – калькулятор рассчитает общую массу изделия. • Второй шаг – если на изделии есть выступы, ступени – надо добавить их габариты. • И третий шаг – вычесть размеры отверстий, выемок, прорезей. • Результат – точная расчетная масса цилиндрической детали.

Масса детали из листа рассчитывается следующим образом:

• В соответствующие поля калькулятора массы внести размерные показатели: ширину, длину, толщину и справочную плотность материала – калькулятор рассчитает общую массу изделия. • Второй шаг – если на изделии есть выступы – надо добавить их габариты. • И третий шаг – вычесть размеры прямоугольных или круглых отверстий. • Результат – точная расчетная масса детали из листа.

Наш калькулятор массы изделий будет полезен как конструктору, так и для заказчиков, ведь он позволяет очень быстро и почти со 100%-точностью получить необходимые данные относительно веса изделия без сложных математических расчетов и процедуры взвешивания.

Обратите внимание, что по умолчанию в калькуляторе стоит масса марки стали 40 ГОСТ 1050-88.

Источник: azmen.a-idea.ru

Источник

Просмотров 3.3к. Опубликовано 28.06.2022

Единицей измерения молекулярной опухоли является л/моль, и эта величина постоянна при нормальных условиях, поэтому молекулярная опухоль составляет 22,4 л/моль.

Как найти объем в химии ℹ️

Вы знаете, что один и тот же химикат любого вещества содержит одинаковое количество структурных единиц. Однако у каждого вещества есть своя структурная единица массы. Поэтому масса одной и той же химической массы разных веществ также отличается.

Молекулярная масса — это масса той части вещества, которая приходится на один моль химической массы.

Молекулярная масса вещества X обозначается символом m(x). Она равна отношению массы конкретного вещества M(x) (г или кг) к химической массе N(x) (моль).

В Международной системе единиц молекулярный вес выражается в кг/моль. В химии чаще используется единица измерения Г/моль.

Определите молекулярную массу углерода. Масса углерода в одном моле стехиометрической массы составляет 0,012 кг или 12 г. Поэтому:.

Молекулярная масса любого вещества численно равна его относительной молекулярной массе, выраженной в Г/моль.

На рисунке 47 показан образец материала (H2O, CACO3

На рисунке 47 показан пример веществ (H2O, CACO3и Zn) с одинаковой химической массой — 1 моль. Как видите, массы различных веществ с одним молем химической массы различны.

Молекулярный вес является важной характеристикой всех образцов.

Молекулярный вес является важной характеристикой всех индивидуальных веществ. Она отражает взаимосвязь между массой вещества и его химическим количеством. Знание одной из этих величин позволяет определить массу другой — химической — величины.

И наоборот, химическое количество по массе:.

А также количество структурных подразделений:.

Связь между свойствами этих трех веществ в их кумулятивном состоянии можно представить с помощью простой диаграммы.

Формула и алгоритм нахождения объёма

Сегодня мы изучаем важный навык в химии — как находить количество различных растворов и других веществ. Эти знания необходимы, потому что они помогут вам решить многие проблемы как в тетради, так и в жизни. Все, что вам нужно знать, — это состоявшийся человек.

Важно понимать, что тип опухоли, которую нужно найти, может варьироваться в зависимости от сущности, которую нужно найти, а точнее, от общего состояния этой сущности. Типы нахождения объемов газа и жидкости противоположны друг другу.

Точный и правильный вид для нахождения объема жидкости: C = n/v.

  1. C – молярная масса раствора (моль на литр).
  2. n – количество вещества (моль).
  3. V – объём вещества-жидкости (литры).

Используя другую задачу и другие данные, существует второй тип для нахождения объема жидкости: v = m/p.

  1. V – объём и измеряется он в миллилитрах.
  2. m – масса, измеряется в граммах.
  3. p – плотность, измеряется в граммах, делённых на миллилитры.

Если в дополнение к объему вам нужно найти массу, вы можете сделать это, зная тип и количество интересующего вас вещества. Используя тип вещества, найдите его молекулярную массу, сложив атомные массы всех элементов, входящих в его состав.

Например, возьмем M(AUSO2). В наших расчетах мы должны получить 197 + 32 + 16 * 2 = 261 г/моль. После этих вычислений находим массу по типу m = n*m: где

  1. m – масса.
  2. n – количество вещества, которое измеряется в молях (моль).
  3. M – молярная масса вещества: граммы, делённые на моль.

Количество вещества обычно указывается в задаче. Если нет, то это может быть опечатка или ошибка в задаче, и вместо того, чтобы пытаться самостоятельно вычислить несуществующую цену, следует обратиться за помощью и объяснениями к преподавателю. В этой статье приведены основные алгоритмы типов и разрешений.

Существует также тип для определения количества газа. Это: v= n*vm:.

  1. V – объём газа (литры).
  2. n – количество вещества (моль).
  3. Vm – молярный объём газа (литры/моль).

Однако существуют определенные исключения. Исключением является то, что при нормальных условиях, т.е. при определенном давлении и температуре, объем газа постоянен и составляет 22,3 л/моль.

Существует и третья вероятность. ... Если сама работа ...

Также возможен третий вариант. Если сама задача содержит уравнения реакций, то решение должно проходить по-другому. Из полученных уравнений вы можете найти количество каждого вещества, равное коэффициенту. Например, Ch4 + 2O2 = CO2+H2O. Из этого уравнения следует, что при взаимодействии 1 моль метана и 2 моль кислорода образуется 1 моль углерода и 1 моль воды. Учитывая, что речь идет о количестве вещества одного компонента, нетрудно найти количества всех остальных веществ. Если количество метана составляет 0,3 моль, то n(Ch4) = 0,6 моль, n(CO2) = 0,3 моль и n(H2O) = 0,3 моль.

б) Газовые законы объем газа

В дополнение к приведенным выше формулам, для решения задач вычислительной химии часто необходимо использовать газовые законы, известные из физики.

При постоянной температуре объем данного количества газа обратно пропорционален давлению, при котором он находится.

При постоянном давлении изменение объема газа прямо пропорционально температуре.

Комбинированный закон Бойля-Мариотта и Гей-Люссака для газов.

Кроме того, если известна масса или количество газа, его объем можно рассчитать по формуле Менделеева-Клапейрона

где n — число молекул вещества, m — масса (г), b — молекулярная масса газа (г/моль) и R — глобальная газовая постоянная, равная 8,31 Дж/(моль х К).

4. определение объема газа очень примитивно, если это газ при почти стандартных условиях. Помните, что один моль газа при этих условиях занимает 22,4 литра. Затем можно произвести расчеты, исходя из заданных условий.

Ключевые слова: решение задач на количество вещества, решение задач по химии на массу и объем, количество содержащегося вещества, количество содержащихся молекул, определение объема (v.o.), обнаружение массы, ее массовые частицы, масса определенных молекул, названия веществ, обнаружение массы молекул, определение абсолютной массы молекул, количество содержащихся атомов, относительная плотность. Определение.

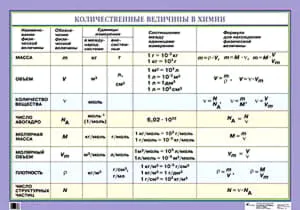
Количество вещества — это число строительных блоков (атомов, молекул, ионов), содержащихся в конкретном образце этого вещества. Единицей измерения количества вещества является моль. Количество вещества (n) связано с числом строительных блоков (N), массой (m) и объемом (V) (для газообразных веществ при температуре нулевой концентрации), содержащихся в образце вещества, следующей формулой

Решение задач с количеством, массой и объемом

В котором.

Vm = 22,4 л/моль (мл/моль, м 3/кмоль) в н.у., Na = 6,02-10 23 (постоянная Авогадро) и молекулярная масса (М) численно равна относительной молекулярной массе вещества:.

Молекулярная масса ...

Существование такой связи означает, что знание одной из величин (количества, массы, объема или числа структурных единиц вещества) позволяет определить все остальные величины.

РЕШЕНИЯ ПРОСТЫХ ЗАДАЧ

Вопрос 1: Сколько вещества содержится в 33 г оксида углерода (IV)?

Ответ: ν(CO2) = 0,75 моль.

Задача № 2. Сколько молекул содержится в 2,5 моль кислорода?

Ответ: n (O2) = 1,505-1024.

Внимание. В этом сборнике лекций вы будете решать задачи общей сложности. Решения сложных задач и задач с кратким ответом см. в конспекте лекций «Решение упражнений по количественным свойствам».

Задача №3. Определите объем (н.у.), занимаемый 0,25 моль водорода.

Задача № 4. Какова масса куска оксида серы (IV) в объеме 13,44 л (об.)?

Вопрос № 5. Если 3 моль кислорода O2Чтобы. Определите массу кислорода, его количество и число молекул кислорода.

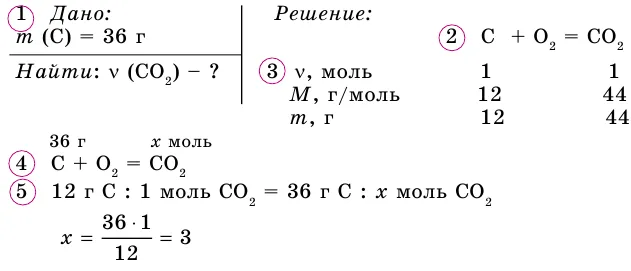
Ответ: m = 96 g- v = 67. 2 l- n(o2) = 1.81-10 24.

Работа №6. масса водорода h2. Определите количество водорода, его количество se. Количество доступных молекул водорода.

Ответ: 5 моль-112 L- 3,01- 10 24.

Работа № 7. Пример количества хлора.2 Н.О.С. Найдите количество хлора, его массу и число молекул хлора.

Ответ: 2,5 моль- 177,5 г- 1,5- 10 24.

Работа № 8. 2.4-10 23. Есть молекулы монооксида углерода (IV) CO2. Определите количество углекислого газа, его массу и количество углекислого газа (Н.С.).

Ответ: 0,4 моль — 17,6 г — 8,96 л.

Вопрос нет. 9. какова масса участка оксида азота (IV), содержащего 4,816-10 23 точки? Каков его объем (Н.С.)?

Вопрос нет. 10. 1,806-10 Масса простого отрезка вещества, содержащего 24 точки, равна 6 г. Определите молекулярный вес вещества и назовите его.

Внимание. В данном пособии рассматриваются задачи нормальной сложности. Нажмите на кнопку ниже, чтобы перейти к решению задач на количество и краткому ответу …

Решайте задачи на количество, массу и объем. Выберите следующие шаги: 1.

4. определение объема газа очень примитивно, если это газ при почти стандартных условиях. Помните, что один моль газа при этих условиях занимает 22,4 литра. Затем можно произвести расчеты, исходя из заданных условий.

Молярный объем: общая информация

Чтобы рассчитать молекулярный вес химического вещества, молекулярный вес вещества делится на его плотность. Таким образом, молекулярный вес рассчитывается по следующему типу

где VM — молекулярный вес вещества, m — молекулярная масса, p — плотность. В международной системе СИ это количество измеряется в кубических метрах на моль (м 3 /моль).

Том ...

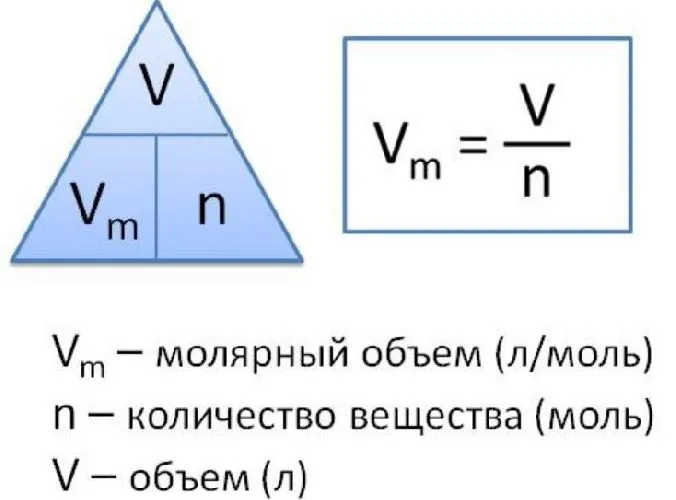
Рисунок 1.Типы молекулярных опухолей.

Молекулярная масса газов отличается от молекулярной массы жидкостей и твердых тел тем, что один молярный элемент газа всегда занимает один и тот же объем (при соблюдении одинаковых параметров).

При расчете объема газа при нормальных условиях, так как объем газа зависит от температуры и давления. Нормальными условиями являются температура 0°C и давление 101 325 кПа.

Молекулярный объем одного моля газа при нормальных условиях всегда одинаков и равен 22,41 DM3 /моль. Этот объем называется молекулярным весом идеального газа. Это означает, что для одного моля газа (кислорода, водорода, воздуха) объем составляет 22,41 дм3 /м.

Молекулярная масса при нормальных условиях может быть получена с помощью законного уравнения для идеального газа, называемого уравнением Клайперона-Менделеева

Где r — глобальная постоянная газа, r = 8,314 дж/моль*k = 0,0821 л*атм/моль k

Объем молярного газа v = rt/p = 8,314*273,15/101,325 = 22,413 л/моль, где t и p — значения температуры (к) и давления при нормальных условиях.

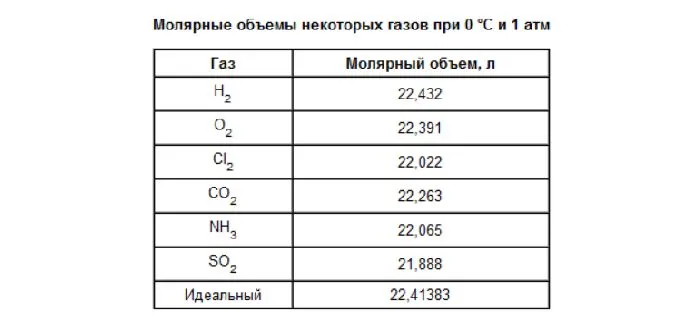
Опухоль ...

Рисунок 2.Таблица молекулярных опухолей.

Закон Авогадро

В 1811 году А. Авогадро предположил, что равные объемы различных газов (температура и давление) содержат одинаковые молекулы. Впоследствии этот случай был подтвержден и стал законом, названным в честь великого итальянского ученого.

Амедео Авогадро

Рисунок 3: Амедео Авогадро.

Закон становится понятным, если вспомнить, что расстояние между частицами в виде газа несравненно больше, чем размер самих частиц.

Таким образом, из закона Авогадро можно сделать следующие выводы.

  • В равных объёмах любых газов, взятых при одной и той же температуре и при одном и том же давлении, содержится одно и то же число молекул.
  • 1 моль совершенно различных газов при одинаковых условиях занимает одинаковый объем.
  • Один моль любого газа при нормальных условиях занимает объем 22,41 л.

Следствия закона Авогадро и понятие молекулярного объема основаны на том, что молекулы любого вещества содержат число частиц (в случае газов и молекул), равное постоянной Авогадро.

Чтобы найти количество молей растворенного вещества в литре раствора, необходимо определить молекулярную концентрацию вещества по формуле c = n / V Где n — количество растворенного вещества, выраженное в молях; V — объем раствора, выраженный в литрах C — молекулярный.

При расчетах газа часто необходимо преобразовать заданные условия в нормальные и наоборот. Таким образом, полезно использовать уравнения, полученные из законов газовой связи Бойля-Мариотта и Гей-Люссака.

Молярный объем

В этом видео учащиеся вспоминают основные формулы и физические величины, знакомятся с новыми понятиями молекулярного объема и учатся решать задачи на основе новых материалов. Это значительно облегчает изучение новых тем.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к видеоурокам этого и других наборов, необходимо приобрести их в каталоге и добавить в личный кабинет.

Конспект урока «Молярный объем»

Молекулярный объем — это объем одного моля вещества. Понятие молекулярного объема применимо к газам. Например, если взять 1 моль воды, то 18 г воды не взвешивают на весах, потому что это совершенно неудобно. Зная, что плотность воды составляет 1 г/мл, мы измеряем ее объем в цилиндре или мензурке.

В этом случае молекулярный объем воды составит 18 мл/моль. Молекулярный объем твердых тел и жидкостей зависит от их плотности. Вода, кислота, сахар и соль имеют разную плотность и, следовательно, разный молекулярный объем.

Если проглотить одну молекулу кислорода, одну молекулу углекислого газа и одну молекулу водорода, то при одинаковых нормальных условиях они занимают одинаковый объем, равный 22,4 л. Эти газы также содержат одинаковое число частиц, т.е. 6,02-1023. Нормальные условия или a.c. — это температура 0°C (градусов Цельсия) и давление 760 мм рт.ст. (миллиметров рт.ст.) или 101,3 кПа (килопаскалей).

Таким образом, молекулярный объем — это объем одного моля газа. Как и другие объемы, он обозначается как молекулярный объем, но с символом V.m .

Молекулярный объем — это также физическая величина, равная отношению объема вещества к количеству вещества. Он может быть записан в следующих типах форматов

Vm =

V — объем газа, а n — количество вещества.

Из этого уравнения также можно найти V.

V = n-Vm

Единицей измерения молекулярной опухоли является л/моль, и эта величина постоянна при нормальных условиях, поэтому молекулярная опухоль составляет 22,4 л/моль.

Объем 1 кмоль называется объемным объемом и измеряется в м 3 / кмоль. То есть 22,4 м 3 / кмоль, а объем 1 ммоль называется объемным объемом и измеряется в мл / моль. Другими словами, объем составляет 22, 4 мл/моль.

Используйте новую формулу для решения задачи.

1. найдите объем азота (N2 ) объемом 2 моль.

Найдите объем азота (N2) в объеме 2 моль. По условию, дано 2 моль азота. Найдите объем азота. Чтобы решить эту задачу, используйте уравнение, чтобы найти объем газа относительно объема вещества. Другими словами, умножьте объем молекулы на объем вещества. Подставьте значение в формулу. То есть 22,4 литра на моль, умноженные на 2 моля, дают 44,8 литра. Таким образом, 2 моль азота занимают объем 44,8 л.

2. найти объем озона (O3 ) имеет объем 67,2 литра.

Согласно этой задаче, учитывая объем озона — 67,2 литра, необходимо найти количество вещества озона. Чтобы решить проблему, используйте тип. Объем делится на молекулярный вес, и значения в формуле обмениваются. Итак, разделив 67,2 литра на 22,4 литра на молекулу, получаем 3 молекулы. Таким образом, 3 моль озона занимают объем 67,2 л.

Таким образом, молекулярный объем — это объем одного моля газа. Как и другие объемы, он обозначается как молекулярный объем, но с символом V.m .

Закон объемных отношений

Если в результате реакции также образуется газ, напишите уравнение реакции между газами.

Соотношение объемов реактора и вещества: 2:1:2. Получим соотношение этих газовых опухолей при нормальных условиях.

Истинно вычислительный

Истинно вычислительный

Как видите, коэффициент газовой опухоли соответствует отношению предыдущего коэффициента типа вещества в уравнении.

В этой же ситуации объемы реакционных газов и газообразных продуктов реакции относятся друг к другу как небольшие целые числа. Это закон Гей-Лоссака о пропорциональности объемов.

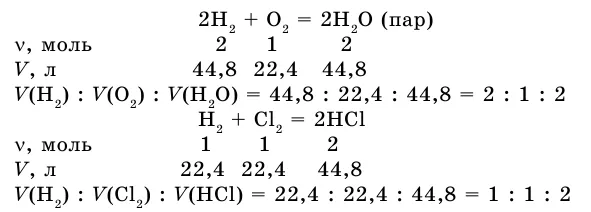
Истинно вычислительный

Из изученных примеров можно сделать вывод, что при решении задачи удобно использовать коэффициенты, так как они указывают на количество вещества в уравнении химической реакции.

Согласно уравнению, определите количество кислорода, необходимое для окисления 60 л серы (IV) оксидом серы (VI).

Истинно вычислительный

  • 1. Моль — мера количества вещества. В 1 моль любого вещества содержится число Авогадро структурных единиц (6,02-1023).
  • 2. Молярная масса вещества (М) численно равна относительной молекулярной массе (Мг).
  • 3. Расчеты по химическим уравнениям производятся на основе закона сохранения масс веществ.
  • 4. В равных объемах газов, взятых при одинаковых условиях, содержится одинаковое число молекул. (Закон Авогадро.)
  • 5. Относительной плотностью одного газа по отношению к другому газу (Dy(X)) называется отношение масс газов, взятых в равных объемах при одинаковых условиях.
  • 6. Объемы реагирующих газообразных веществ относятся между собой и к объемам образующихся газообразных продуктов, как небольшие целые числа, равные коэффициентам в уравнении химической реакции. (Закон объемных отношений Гей-Люссака.)
  • 7. При нормальных условиях (н. у.) любой газ занимает 22,4 л. Эта величина называется молярным объемом (У = 22,4 л/моль).

Услуги в области химии:.

Лекции по химии:.

Лекции по неорганической химии:.

Лекции по органической химии:.

Отправляйте задания в любое время дня и ночи

Официальный сайт Брилёновой Натальи Валерьевны, профессора факультета информатики Екатеринбургского государственного института.

Все права интеллектуальной собственности на загруженный материал сохраняются за бенефициарами этого материала. Коммерческое и/или иное использование запрещено за пределами материалов предварительного изучения NataliblileNova.ru. Публикация и распространение опубликованных материалов не предназначены для получения коммерческой и/или иной выгоды.

Этот сайт предназначен для облегчения образовательного пути студентов. Наталья Брилёнова не предлагает и не оказывает товары и услуги.

Обязательно ссылайтесь на сайт Natalibrilenova.ru в случае создания копий материалов.

Источник

Средней
плотностью
называют массу единицы объема материала
в естественном состоянии, т.е. вместе с
порами и пустотами. Средняя плотность
определяется по формуле:

0=,
[г/см3], (3.1)

где m
– масса образца,
г;

V
– объем образца в естественном состоянии,
см3.

Для вычисления
средней плотности материала определяют
массу образца и его объем в естественном
состояния. Одно и то же количество
материала в естественном состояние
занимает больший объем, чем в плотном.
Поэтому средняя плотность каменных
материалов всегда меньше истинной
плотности.

В практике
определения средней плотности твердого
материала возможны два случая:

а) образец материала
имеет правильную форму;

б) образец имеет
неправильную форму.

Среднюю плотность
материала можно определять руководствуясь
ГОСТ 30629-99, в соответствии с изложенной
ниже методикой.

3.1. Определение
средней плотности образцов правильной
формы

Образцы правильной
геометрической формы должны иметь
наименьшее измерение не менее 10 см, если
материал пористый, и не менее 4 см, если
материал плотный. Испытания проводят
на 5-ти образцах кубической или
цилиндрической формы. Образцы взвешивают
на технических весах с точностью до 0,1
г, (если масса образца менее 500 г). Перед
взвешиванием образцы должны быть
высушены до постоянной массы.

Для определения
объема образцы измеряют с помощью
штангенциркуля с точностью до 0,1 мм.
Например, если измеряемый образец имеет
форму куба или параллелепипеда, то
каждую грань измеряют в трех местах по
длине, ширине, высоте (рис.3.1.). За
окончательный размер каждой грани
принимают среднее арифметическое трех
измерений. Объем образца получают
перемножением средних размеров трех
граней образца.

Рис.3.1. Схема
измерения образцов правильной
геометрической формы

Среднюю плотность
вычисляют по формуле:

0=,
[г/см3], (3.2)

Для обеспечения
точности результатов среднюю плотность
вычисляют как среднее арифметическое
пяти определений.

3.2. Определение
средней плотности образцов неправильной
формы

При работе с
образцами неправильной формы, сложность
представляет измерение объема. В этом
случае определение производят методом
гидростатического взвешивания или с
помощью объемомера.

Точность такого
определения в
значительной
степени зависит от пористости материалов,
так как образец, погружаемый в воду, не
только вытесняет, но и частично впитывает
ее в свои поры, а это приводит к искажению
результатов.

3.2.1. Определение
средней плотности методом гидростатического
взвешивания

Независимо от
метода определения средней плотности
перед определением объема образец либо
насыщают водой до постоянной массы,
т.е. до полного заполнения пор, либо
покрывают его поверхность водонепроницаемым
слоем предварительно расплавленного
парафина.

Опыт выполняют
следующим образом. На поверхность
предварительно высушенного и взвешенного
с точностью до 0,01 г образца небольшой
кистью или погружением в расплав наносят
тонкий слой парафина. Охлажденный
образец снова взвешивают вместе с
парафином. Объем парафина на образце
вычисляют по формуле:

,
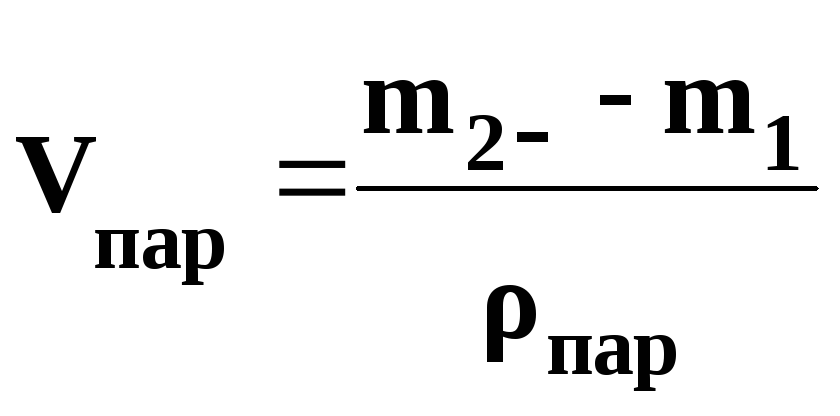[cм3], (3.3)

где m1
 – масса
образца на воздухе без парафина, г;

m2
– масса образца на воздухе с парафином,
г;

Vпар–
объем парафина, см3;

пар–
средняя плотность парафина, г/см3,
(0,93 г/см3).

Взвешивание образца
в воде осуществляется следующим образом:
образец, покрытый парафином, подвешивают
к коромыслу весов и погружают в сосуд
с водой так, чтобы он не касался стенок,
и взвешивают (рис. 3.2.).

Величину средней
плотности образца материала определяют
по формуле:

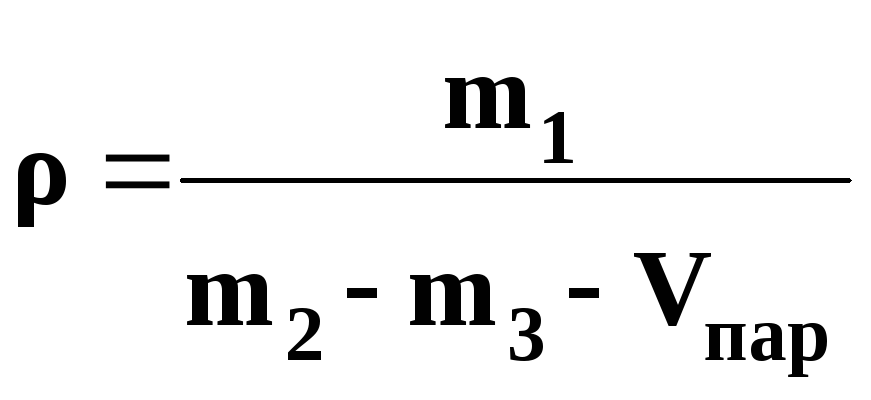,[г/см3], (3.4)

где m1
 – масса
образца на воздухе без парафина, г;

m2
– масса образца на воздухе с парафином,
г;

m3
– масса образца с парафином в воде, г;

Vпар–
объем парафина, см3.

Среднюю плотность
материала вычисляют как среднее
арифметическое результатов определений
средней плотности пяти образцов.
Расхождение между результатами
параллельных определений средней
плотности материала не должно превышать
20 кг/м3.

Рис. 3.2. Весы для
гидростатического взвешивания

3.2.2. Определение
средней плотности с помощью обьемомера

Определить среднюю
плотность можно также при помощи
объемомера (рис.3.3).

В объемомер с
избытком наполняют воду и ждут, пока
избыток стечет. Затем под горловину
подставляют взвешенный стакан. Каждый
образец высушивают, взвешивают, покрывают,
как и в предыдущем опыте, слоем
расплавленного парафина, привязывают
на прочную нить и вторично взвешивают.
При погружении испытуемого образца в
обьемомер вытесняемая вода будет
вытекать из горловины в стакан. После
того. как вытекание воды прекратится,
стакан с водой взвешивают и определяют
мaccy
воды, вытесненную образцом. Среднюю
плотность образца вычисляют по формуле:

0=,
[г/см3], (3.5)

где m1
– масса сухого образца, г;

V1
– объем
образца с парафином (равный массе воды,

вытесненной образцом, см3.

Vпар–
объем парафина, см3.

Объем парафина
Vпар,
затраченного на покрытие образца
определяют по формуле:

Vпар=,
[cм3], (3.6)

где m1
 – масса
образца на воздухе без парафина, г;

m2
– масса образца на воздухе с парафином,
г;

пар–
средняя плотность парафина, г/см3,
(0,93 г/см3).

Рис. 3.3. Объемомер:

1 — цилиндрический
сосуд; 2 — горловина; 3 — стакан; 4 —
образец

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Добавить комментарий