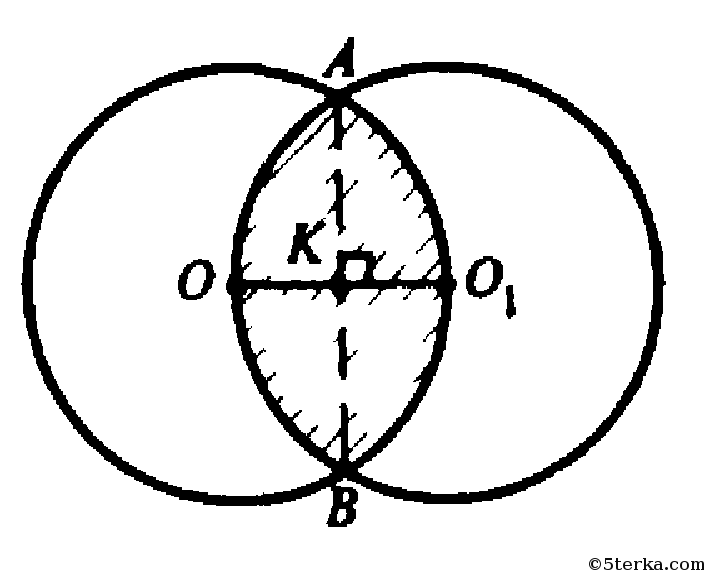
Cечение шаров проходит через их центры О и О1. Хорда АВ⊥ОО1, ОО1=r, r — радиусы шаров. Общая часть заштрихована и состоит из двух одинаковых шаровых сегментов. Их объемы:
Объем шара
Задача 1.
Объем шара находят по формуле
V=4πR³:3
Объем цилиндра находят по формуле
V= πR²h
4πR³:3=πR²h сократим одинаковые члены уравнения
h=4R:3
———–
Задача 2.
Два равных шара расположены так, что центр одного лежит на поверхности другого.Как относится объём общей части шаров к объёму одного шара?
Объем шара
V=4 π R³:3
Объем шарового сегмента
V=π h²( R−1/3 h)
объём общей части шаров= 2 π h²( R−1/3 h
Отношение ообъема бщей части к объему одного шара
2 π h²( R−1/3 h)
4 π R³:3
После сокращения получим
h²( R−1/3 h)3
2 R³
Но высота сегмента здесь равна половине радиуса,
вместо h нужно подставить ¹/₂ R и затем упростить.
⅟₄ R² ( R−1/6 R)3
2 R³
23.1. Объем и площадь боковой поверхности цилиндра
Найдем объем и площадь боковой поверхности
прямого цилиндра радиусом
и высотой
.
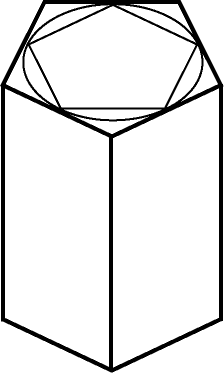
Впишем в цилиндр и опишем вокруг него
по прямой
-угольной
призме с высотой
.
Тогда объем цилиндра будет заключен в
следующих границах:
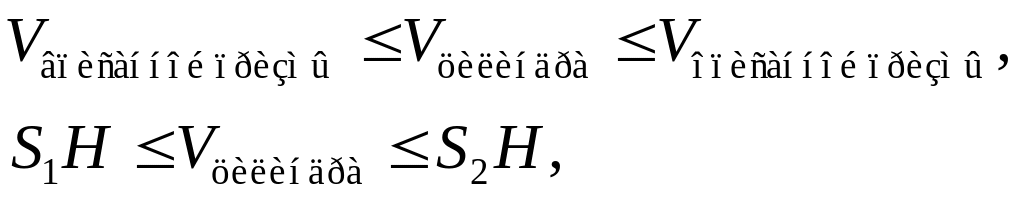
где
и
– площади оснований вписанной и описанной
призмы.
Устремим число
к бесконечности. Тогда площади
-угольной
в основании призм будут стремиться к
площади основания цилиндра и по теореме
о предельном переходе в неравенствах,
получим объем цилиндра равен произведению
площади основания на высоту
.
Аналогичным образом периметры оснований
призм будут стремиться к пирометру
основания цилиндра, и площадь боковой
поверхности цилиндра равняется
произведению длины окружности на высоту
.
23.2. Объем и площадь боковой поверхности конуса
Найдем объем и площадь боковой поверхности
прямого конуса радиусом
и высотой
.

Впишем в цилиндр и опишем вокруг него
по прямой
-угольной
пирамиде с высотой
.
Тогда, проводя рассуждения, аналогичные
приведенным в предыдущем разделе,
получаем, что объем конуса равен одно
трети произведения площади основания
на высоту
,
площадь боковой поверхности равняется
произведению полупериметра основания
на образующую (которая в пределе
совпадает с апофемами вписанной и
описанной пирамид)
.
23.3. Объем шара и площадь сферы
Объем любого тела, образованного
вращением кривой
(
)
вокруг оси абсцисс, может быть вычислен
по формуле:
.
Поскольку поверхность шара может быть
получена вращением половины окружности
,
то объем шара можно вычислить по
вышеприведенной формуле, где
при
:

Таким образом, объем шара радиусом
равняется
.
Площадь поверхности любого тела вращения
может быть рассчитана по формуле:
.
Тогда для площади поверхности сферы,
где
имеем:
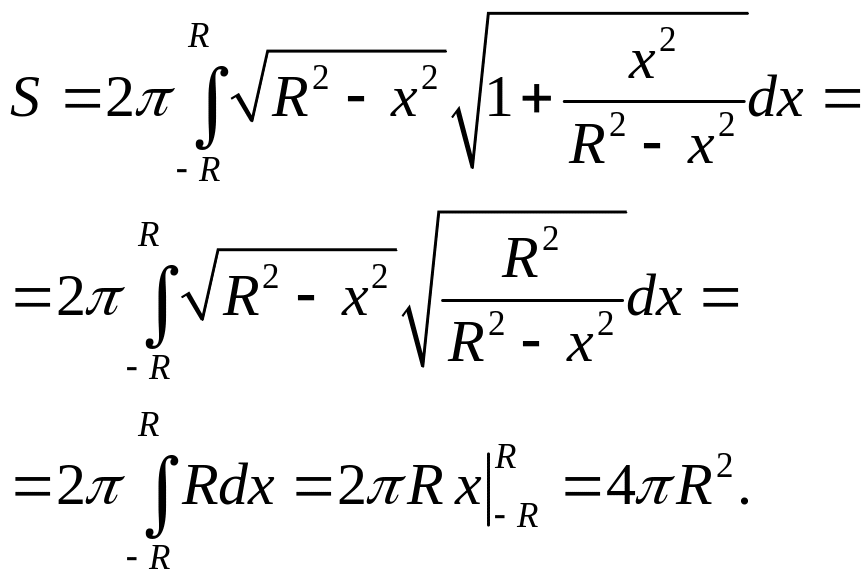
Таким образом, площадь поверхности
сферы радиусом
равняется
.
23.4. Объем шарового сектора и шарового сегмента
Шаровым сегментом называется часть
шара, отсекаемая от него плоскостью.
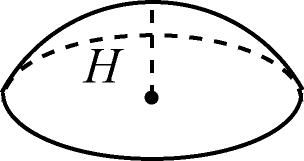
Формула для объема шарового сегмента
высотой
получается аналогично формуле для
объема шара:
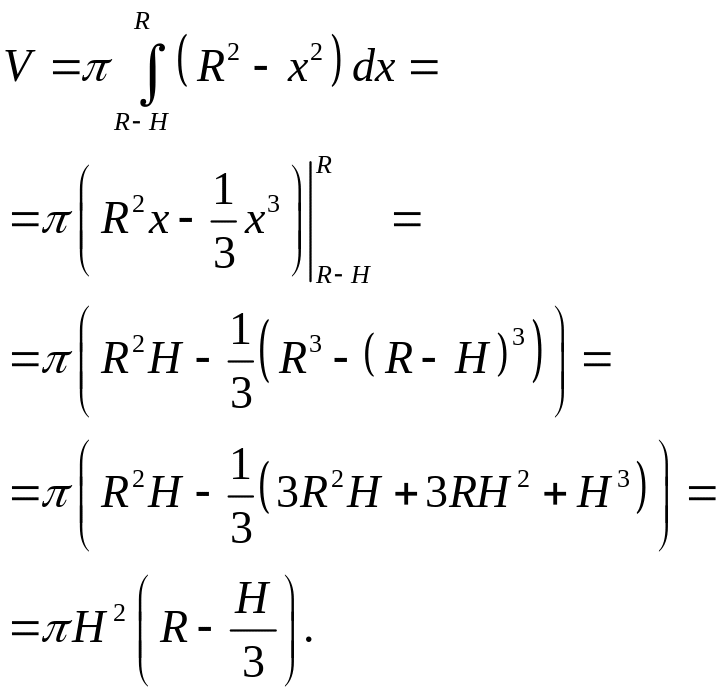
Шаровым
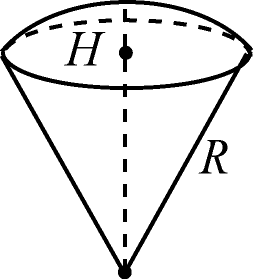
сектором называется тело, которое
получается из шарового сегмента и
конуса, вершиной которого является
центр шара, а основание совпадает с
основанием сегмента.
Объем шарового сектора получается как
сумма объемов сегмента высотой
и конуса с радиусом основания
и высотой
:
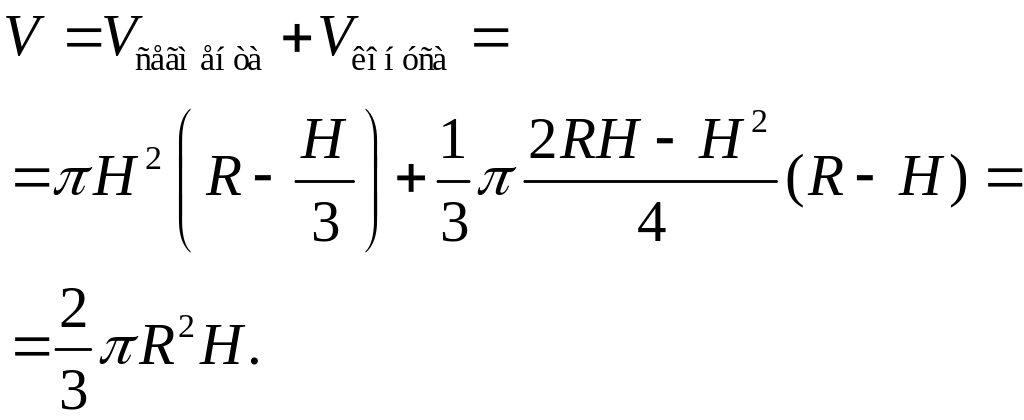
Задачи
-
В цилиндр вписана правильная треугольная
призма, а в призму вписан цилиндр. Найти
отношение объемов цилиндров. -
Осевым сечение конуса является
равнобедренный прямоугольный треугольник
с площадью 9. Найти объем конуса. -
Равносторонний треугольник вращается
вокруг своей стороны.
Найти объем полученного тела вращения. -
Найти объем усеченного конуса с
радиусами оснований
и
и высотой
.
-
Усеченный конус, у которого радиусы
оснований 4 и 22, и равновеликий цилиндр
имеют одинаковую высоту. Чему равен
радиус основания цилиндра? -
Из деревянного цилиндра, высота которого
равна диаметру основания, выточен
наибольший шар. Сколько процентов
материала сточено? -
Два равных шара расположены так, что
центр одного лежит на поверхности
другого. Как относится объем общей
части шаров к объему целого шара? -
Диаметр шара, равный 30, является осью
цилиндра, у которого радиус основания
равен 12. Найти объем части шара,
заключенной внутри цилиндра. -
Шар радиуса 10 цилиндрически просверлен
по оси. Диаметр отверстия равен 12. Найти
объем тела. -
Полукруг свернут в коническую
поверхность. Найти угол между образующей
и осью конуса. -
Доказать, что полная поверхность
равностороннего конуса равновелика
поверхности шара, построенного на его
высоте как на диаметре.
21
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
[03.12.2013 20:10]
Решение 1881:
Два равных шара расположены так, что центр одного лежит на поверхности другого. Как относитс
…
Подробнее смотрите ниже
Номер задачи на нашем сайте: 1881
ГДЗ из решебника:
Тема:
23. Объемы и поверхности тел вращения
Нашли ошибку? Сообщите в комментариях (внизу страницы)
|
Раздел: Геометрия Полное условие: Два равных шара расположены так, что центр одного лежит на поверхности другого. Как относится объем общей части шаров к объему целого шара?Решение, ответ задачи 1881 из ГДЗ и решебников: Этот учебный материал представлен 1 способом:
|
||
| Счетчики: 4348 | Добавил: Admin |
| Добавить комментарий
Добавлять комментарии могут только зарегистрированные пользователи. [ Регистрация | Вход ] |
Слайды и текст этой презентации
Слайд 1
Зачет по теме: «Объем шара, его частей» и

«Площадь сферы»
МКОУ «Погорельская СОШ»
Слайд 2
Формулы
V=πR2H
V=1/3∏R2H
V=1/3∏H(R2+r2+Rr)
V=4/3∙∏R3

Слайд 3
Площадь сферы равна:
S = 4πR2 ,
где R

– это радиус сферы
Объем шара равен:
V = 1⅓πR3 =
4/3πR3
где R – это радиус шара
Объем шарового сегмента равен:
V
=πh2( R – ⅓h) ,
где R – это радиус шара, а h – это высота сегмента
Объем шарового слоя равен:
V = V1 – V2 ,
где V1 – это объем одного шарового сегмента, а V2 – это объем второго шарового сегмента
Объем шарового сектора равен:
V = ⅔πR2h ,
где R – это радиус шара, а h – это высота шарового сегмента
Формулы для вычисления объема:
шара, шарового сектора, шарового слоя, шарового сектора и площади сферы
Слайд 4
Теоретический диктант
Вариант 1
Вписать в текст недостающие по

смыслу слова.
Всякое сечение шара плоскостью есть круг. Центр этого
круга есть …………………… перпендикуляра , опущенного из центра шара на
секущую плоскость.
2. Центр шара является его ………………….……. симметрии.
3. Осевое сечение шара есть ………………………….
4. Линии пересечения двух сфер есть…………………
5. Плоскости, равноудаленные от центра, пересекают шар по ………………кругам.
6. Около любой правильной пирамиды можно описать сферу , причем ее центр лежит на ……………….. пирамиды.
основание
центром
круг
окружность
равным
высоте
Слайд 5
Теоретический диктант
Вариант 2
Вписать в текст недостающие по

смыслу слова.
Любая диаметральная плоскость шара является его ………………… симметрии.
2.
Осевое сечение сферы есть………………..
3. Центр шара ,
описанного около правильной пирамиды , лежит на …………………. пирамиды.
4. Радиус сферы , проведенный в точку касания сферы и плоскости ………………………………………..к касательной плоскости.
5. Касательная плоскость имеет с шаром только одну общую точку …………………….
6. В любую правильную пирамиду можно вписать сферу , причем ее центр лежит на ……………… .…….пирамиды.
плоскостью
окружность
высоте
перпендикулярен
касания
высоте
Слайд 6
Карточка №1
Плоскость перпендикулярная диаметру шара, делит его части

3см и 9см. Найдите объем шара?
288П см³
Карточка №2
Два равных
шара расположены так, что центр одного лежит на поверхности другого.
Как относится объем общей части шаров к объему целого шара?
Карточка №3
Какую часть объема шара составляет объем шарового сегмента, у которого высота равна 0,1 диаметра шара, равного 20см?
5/16
0,028
Слайд 7
Задача №1
Объем шара радиуса R равен V. Найдите:

объем шара радиуса: а) 2R б) 0,5R
Задача №2
Чему
равен объем шарового сектора, если радиус окружности основания равен 60см,
а радиус шара-75см.
Слайд 8
БЫСТРО И КРАТКО НАПИШИТЕ ОТВЕТЫ

НА ВОПРОСЫ:
Сколько сфер можно провести:
а) через одну и
ту же окружность;
б) через окружность и точку, не принадлежащую
её плоскости?
2. Сколько сфер можно провести через четыре точки, являющиеся вершинами:
а) квадрата;
б) равнобедренной трапеции;
в) ромба?
3. Верно ли, что через любые две точки сферы проходит один большой круг?
4. Через какие две точки сферы можно провести несколько окружностей большого круга?
5. Как должны быть расположены две равные окружности, чтобы через них могла пройти сфера того же радиуса?
одну
бесконечно
Ни одной
бесконечно
бесконечно
Нет
Диаметрально противоположные
Иметь общий центр
Слайд 9
Теоретический диктант
Вариант 2
Вписать в текст недостающие по

смыслу слова.
Любая диаметральная плоскость шара является его ………………… симметрии.
2.
Осевое сечение сферы есть………………..
3. Центр шара ,
описанного около правильной пирамиды , лежит на …………………. пирамиды.
4. Радиус сферы , проведенный в точку касания сферы и плоскости ………………………………………..к касательной плоскости.
5. Касательная плоскость имеет с шаром только одну общую точку …………………….
6. В любую правильную пирамиду можно вписать сферу , причем ее центр лежит на ……………… .…….пирамиды.
плоскостью
окружность
высоте
перпендикулярен
касания
высоте
Слайд 10
Тестовая самостоятельная работа ур.52
Уровень1 Вариант 1
1.На расстоянии 12

см от центра шара проведено сечение, радиус которого равен
9см. Найдите объем шара и площадь его поверхности.
2. Сфера радиуса
3см имеет цент в точке О (4;-2;1). Составьте уравнение сферы, в которую перейдет данная сфера при симметрии относительно плоскости ОХУ. Найдите объем шара, ограниченного данной сферой.
Уровень 1 Вариант 2
1.Через точку, лежащую на сфере, проведено сечение радиуса 3см под углом 60° к радиусу сферы, проведенному в данную точку. Найдите площадь сферы и объем шара.
2. Сфера радиуса 3 имеет центр в точке О (-2;5;3). Составьте уравнение сферы, в которую перейдет данная сфера при симметрии относительно плоскости ОХZ. Найдите площадь данной сферы.
Слайд 11
Тестовая самостоятельная работа ур.52
Уровень2 Вариант 1
1.На расстоянии 2√7см

от центра шара проведено сечение. Хорда этого сечения, равна
4см, стягивая угол 90°. Найдите объем шара и площадь его
поверхности.
2. Сфера с центром в точке О (2;1;-2) проходит через начало координат. Составьте уравнение сферы, в которую перейдет данная сфера при симметрии относительно оси абцисс. Найдите объем шара, ограниченного полученной сферой.
Уровень2 Вариант 2
1.На расстоянии 4см от центра шара проведено сечении. Хорда, удаленная от центра этого сечения на √5см, стягивая угол 120°. Найдите объем шара и площадь его поверхности.
2. Сфера с центром в точке О (-1;-2;2) проходит через начало координат. Составьте уравнение сферы, в которую перейдет данная сфера при симметрии относительно плоскости Z=1. Найдите площадь сферы.
Слайд 12
Вариант 1
Радиус шара ¾ дм. Вычислите объём шара

и площадь сферы.
2. Футбольный мяч имеет диаметр 30 дм.
Какой объём воздуха содержится в мяче?
Вариант 2
Диаметр шара ½
дм. Вычислите объём шара и площадь сферы.
2. Волейбольный мяч имеет радиус 12 дм. Какой объём воздуха содержится в мяче?
Самостоятельная работа
Слайд 13
Вариант 1
Записать формулы площади сферы, объема шара и

его частей.
Решить задачи:
№1. Объем шара равен 36Псм³. Найдите площадь
сферы, ограничивающей данный шар.
№2. В шаре радиуса 15см проведено сечение,
площадь которого равна 81см². Найдите объем меньшего шарового сегмента, отсекаемого плоскостью сечения.
№3. Найдите объем шарового сектора, если радиус шара равен 6см, а высота соответствующего сегмента составляет шестую часть диаметра шара.
Вариант 2
Записать формулы площади сферы, объема шара и его частей.
Решить задачи:
№1. Площадь поверхности шара равна 144П см². Найдите объем данного шара.
№2. На расстоянии 9м от центра шара проведено сечение, длина окружности которого равна 24П см. Найдите объем меньшего шарового сегмента, отсекаемого плоскостью сечения.
№3. Найдите объем шарового сектора, если радиус шара равен 6см, а высота конуса, образующего сектор, составляет треть диаметра шара.
Самостоятельная работа
Слайд 14
Дано: шар; V=113,04 см³,
Найти: R, S.
Дано:

шар; S=64π см²
Найти : R, V
3. Дано: шаровой
сегмент, r осн.=60 см, Rшара=75 см.
Найти: Vшарового сегмента.
Решение задач с
самопроверкой.
Решение: V=πh²(R-⅓h) О₁С=√R²-r²=√75²-60²=45
h= ОС-ОС₁=75-45=30 V=π·30²·(75-⅓·30)=58500π.
Ответ: 58500π.
Решение: S=4πR², 64π=4πR², => R=4
V=4πR³/3, V=4π4³/3=256π/3.
Ответ: 4,256π/3.
Решение: V=4πR³/3, => 113,04=4πR³/3 => R³=27, R=3.
S=4πR², S=4π3²=36π.
Ответ: 3,36π.
Слайд 15
Отрази свое настроение смайликом.
Рефлексия
Возьмите смайлик соответствующий Вашему настроению

на конец урока и, уходя прикрепите его на доске
с магнитной основой.
Слайд 16
Домашнее задание
Повторить формулы объемов шара, шарового сегмента,

шарового слоя, шарового сектора. №723, №724, №755
Учебник по геометрии
10-11 класс Атанасян Л.С., 2008 год
Гаврилова Н.Ф. Поурочные разработки по
геометрии 11 класс
Литература и интернет ресурсы



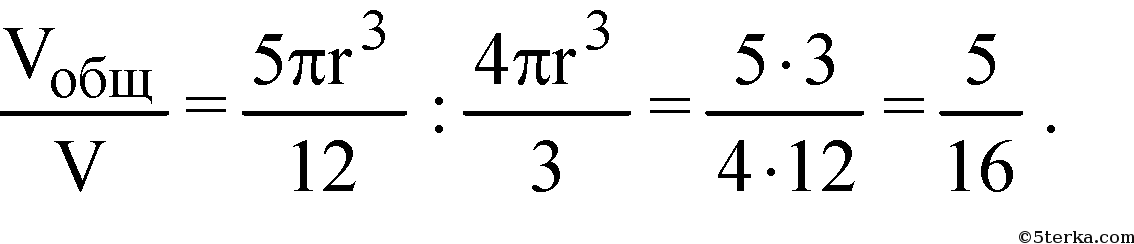

 Для просмотра в натуральную величину нажмите на картинку
Для просмотра в натуральную величину нажмите на картинку
