Перейти к содержанию
Калькуляторы объёма и площади круга, цилиндра, куба, шара (сферы), конуса
На чтение 1 мин Просмотров 29.2к.
Обновлено 10.01.2022
Содержание
- Калькулятор площади и периметра (длины окружности) круга
- Калькулятор расчета площади и объёма шара (сферы)
- Калькулятор расчета объёма цилиндра
- Калькулятор расчета объёма параллелепипеда
- Калькулятор куба-объём, площадь поверхности
 В данном разделе вы найдете сборник калькуляторов на простые фигуры и рассчитать такие параметры как площадь, объем, периметр и прочие значения
В данном разделе вы найдете сборник калькуляторов на простые фигуры и рассчитать такие параметры как площадь, объем, периметр и прочие значения
Калькулятор площади и периметра (длины окружности) круга

Калькулятор расчета площади и объёма шара (сферы)

Калькулятор расчета объёма цилиндра

Калькулятор расчета объёма параллелепипеда

Калькулятор куба-объём, площадь поверхности

Длина окружности

О чем эта статья:
6 класс, 9 класс, ЕГЭ/ОГЭ
Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так – l
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Как найти длину окружности через диаметр
Хорда — это отрезок, который соединяет две точки окружности.
Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:
π— число пи — математическая константа, примерно равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, примерно равное 3,14
r – радиус окружности
Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, примерно равное 3,14
S — площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, примерно равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
π – математическая константа, примерно равная 3,14
a – сторона квадрата
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, примерно равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен Подставим туда наши переменные и получим
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Обучение на курсах по математике поможет закрепить полученные знания на практике.
Как посчитать длину окружности
Онлайн калькулятор
Как посчитать длину окружности зная диаметр
Какая длина у окружности если
Какова длина окружности (С) если её диаметр d?
Формула
С = π⋅d , где π ≈ 3.14
Пример
Если диаметр круга равен 1 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная радиус
Какая длина у окружности если
Какова длина окружности (С) если её радиус r?
Формула
С = 2⋅π⋅r , где π ≈ 3.14
Пример
Если радиус круга равен 0.5 см, то его длина примерно равна 3.14 см.
Как посчитать длину окружности зная её площадь
Какая длина у окружности если
Какова длина окружности (С) если её площадь S?
Формула
С = 2π⋅ √ S /π , где π ≈ 3.14
Пример
Если площадь круга равна 6 см 2 , то его длина примерно равна 8.68 см.
Длина окружности
Длина окружности
Длина любой окружности больше своего диаметра в одно и то же число раз, а именно, приблизительно в 3,14 раза. Для обозначения этой величины используется маленькая (строчная) греческая буква π (пи):
Таким образом, длину окружности (C) можно вычислить, умножив константу π на диаметр (D), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
где C — длина окружности, π — константа, D — диаметр окружности, R — радиус окружности.
Так как окружность является границей круга, то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Решение: Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см).
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Решение: Сначала найдём диаметр окружности, умножив длину радиуса на 2:
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м).
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Решение: Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π:
следовательно, радиус будет равен:
| R | ≈ | 7,85 | = | 7,85 | = 1,25 (м). |
| 2 · 3,14 | 6,28 |
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Решение: Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2 ).
Ответ: 12,56 см 2 .
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Решение: Сначала найдём радиус круга, разделив его диаметр на 2:
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2 ).
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 · | 7 2 | = 3,14 · | 49 | = |
| 4 | 4 | 4 |
| = | 153,86 | = 38,465 (см 2 ). |
| 4 |
Ответ: 38,465 см 2 .
Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .
Решение: Чтобы найти радиус круга по его площади, надо площадь круга разделить π, а затем из полученного результата извлечь квадратный корень:
[spoiler title=”источники:”]
http://poschitat.online/dlina-okruzhnosti
http://izamorfix.ru/matematika/planimetriya/dlina_okruj.html
[/spoiler]
При помощи нашего калькулятора вы легко сможете узнать объем цилиндра. Так же если вам необходимо узнать объем бочки, круглой цистерны, круглого бака и т.д., то это калькулятор то, что Вам нужно.
|
|
|
| Вычислить объем цилиндра через: | |
| Длина радиуса R: | |
| Высота цилиндра h: |
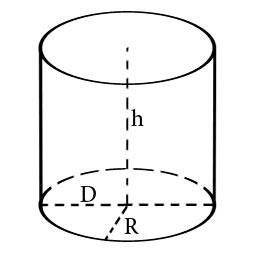
Для того что бы вычислить объем цилиндра необходимо знать его высоту и радиус или диаметр. Если нам известны указанные величины, для нас не составит труда вычислить объем.
Объем цилиндра рассчитывается по следующим формулам:
- Если нам известен радиус:
V=πR2h
- Если нам известен диаметр:
V=πD2/4h
Где V – объем, R – радиус, D – диаметр, h – высота, π – число Пи которое всегда примерно равно 3,14.
Расчет объема цилиндра |
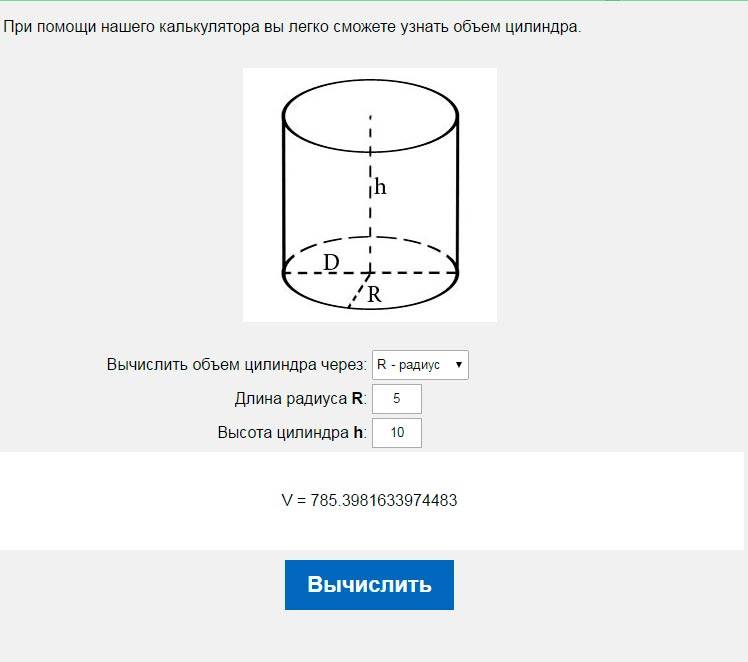 |
Formula.co.id – В этой статье мы узнаем, как рассчитать объем круга. Раньше мы уже знали, что такое круг, потому что с начальной школы мы выучили то, что называется кругом, потому что поэтому без необходимости задерживаться Опять же, давайте вместе обсудим формулу объема круга, и позже она будет сопровождаться примерами вопросов об объеме круга в качестве учебного материала для студентов. читатель.
Оглавление :
Определение Круга
Само определение круга – это набор всех точек на плоскости, которые равноудалены от фиксированной точки на плоскости. Тогда неподвижная точка называется центром круга, а расстояние от точки на окружности до его центра называется радиусом окружности.
Чтобы было понятнее значение самого круга, здесь мы подробно объясним элементы круга, обратите внимание на изображение круга ниже:
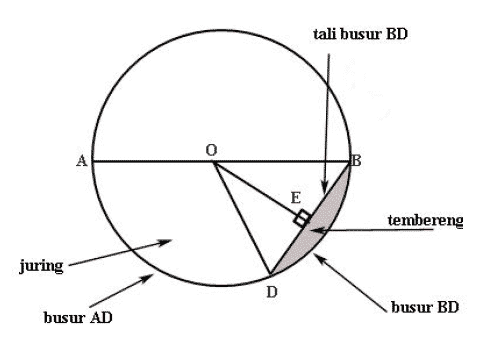
Элементы круга
- Центр круга – это точка, расположенная в середине круга.
- радиус круга ( р ) – это линия от центра окружности до кривизны окружности.
- Диаметр ( d ) представляет собой прямую, соединяющую 2 точки на кривизне окружности, проходящей через центральную точку.
- Дуга окружности – это изогнутая линия, лежащая на кривой окружности, соединяющей любые 2 точки на кривой.
- Круговая хорда – это прямая линия в окружности, соединяющая 2 точки кривизны окружности.
- Уклон – это область в окружности, ограниченная дугой и хордой.
- Радиус – это область в круге, ограниченная двумя радиусами круга, и дугой, примыкающей к двум радиусам круга.
- Апофема – это линия, соединяющая центр круга с хордой круга. Линия перпендикулярна хорде окружности.
Продолжайте обсуждать свойства кругов.
Характеристики кругов
- У круга только одна сторона.
- Круг обладает бесконечной симметрией вращения.
- У круга бесконечная симметрия и оси.
- Но у круга нет вершин.
Формула объема круга
Для получения более подробной информации на сайте formula.co.id будут обсуждаться все формулы для круга, будь то формула площади, окружности и объема самого круга. Для получения более подробной информации о формуле, рассмотрите объяснение формулы ниже:
Формула объема круга:
V = х г2
Формула окружности круга:
К = 2 х х г
Формула площади круга:
L = х г2
Информация :
- = 22/7 или 3,14
- r = радиус (см)
Вам необходимо знать, что приведенная выше формула для площади и объема одинакова, но для определения объема число должно быть в одной и той же единице, а именно в кубических единицах или (см).3 ). Переходя к последнему обсуждению, formula.co.id предоставит вам пример вопроса с кругом, чтобы вы все лучше поняли формулу круга.
Пример круга
- Если круг имеет диаметр 80 см, какова площадь полукруга?
Отвечать:
Известен = d = 80 см
r = 80 см: 2 = 40 см
Спрошено = площадь полукруга?
Площадь полукруга = x r2
= 3,14 х 40 см х 40 см: 2
= 3,14 х 40 см х 40 см: 2
= 2512 см2
Итак, площадь полукруга составляет 2512 см.2
- Круг имеет радиус 14 см, какова длина окружности круга?
Отвечать:
Известен = r = 14 см
Спрошено = окружность круга?
Периметр = K = 2. π. р
= 2 х 22/7 х 14 см
= 88 см
Итак, окружность круга 88 см.
Таким образом, полный математический материал о круге, будь то понимание, элементы, свойства, примеры задач и формула для объема круга сфер, которые могут быть переданы, могут быть полезны …
Другие формулы:
- Формула объема блока
- Формула объема цилиндра
Расчет объема цилиндра в м3 онлайн сегодня не проблема. Для тех, кому надо срочно сделать подобные исчисления, разработаны специальные сервисы. Рассчитать объем цилиндра в онлайн-калькуляторе очень просто. Для этого потребуется лишь знать его величины.
Как происходит расчет
Пользователь должен знать:
- высоту цилиндра;
- радиус его основания;
- площадь основания.
Программа выдаст детальное описание примера, его пошаговое решение и вы сможете понять, по какому алгоритму решалась задача. Это позволяет закрепить выученные сведения. При этом используется формула объема цилиндра, и вы можете узнать величину в литрах.
Чтобы рассчитать объем, нужно внести в строку известные вам величины, ввести все цифровые данные и нажать кнопку «рассчитать объем». Через несколько секунд программа выдаст вам не только решение, но и его объяснение!
По высоте и радиусу
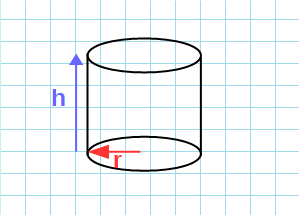
Формула объема цилиндра через высоту и радиус:
V=π·r²·h
π – константа равная (3.14); r – радиус основания; h – высота цилиндра.
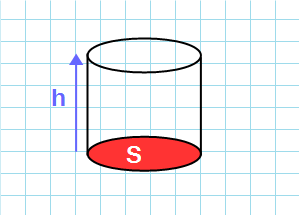
Через площадь основания и высоту
Ответы:
Формула объема цилиндра через высоту и площадь основания:
V=S·h
S – площадь основания цилиндра; h – высота цилиндра.