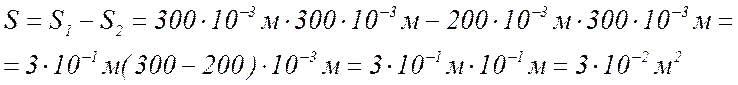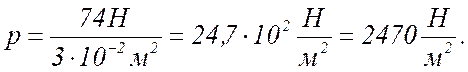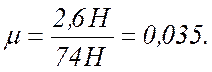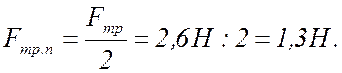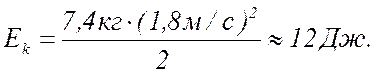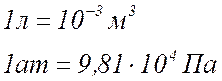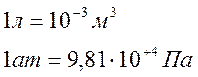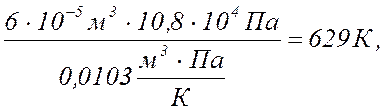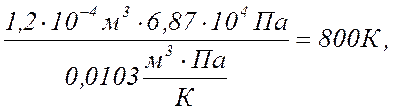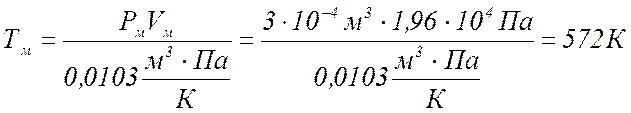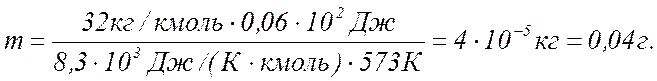Давление зависит от силы, с которой тело давит на опору и площади соприкосновения. Если тело давит под действием силы тяжести на наклонную опору, то формула такая P=mg*cosα/S, где α — угол между горизонталью и опорой.
Чем больше площадь опоры, тем меньшее давление производят на поверхность, а чем меньше площадь опоры,тем больше давление производят на поверхность.
Например: человек на лыжах производит меньшее давление на снег, чем без лыж( по нашему вышеописанному свойству)
OBRAZOVALKA.COM
OBRAZOVALKA.COM — образовательный портал
Наш сайт это площадка для образовательных консультаций, вопросов и ответов для школьников и студентов .
На вопросы могут отвечать также любые пользователи, в том числе и педагоги.
Консультацию по вопросам и домашним заданиям может получить любой школьник или студент.
Баумгертнер ·
19.11.2020 15:34
Ответов: 1
Показать ответы
0 Обсудить
Ответы
у нас изотерма, так что по закону клапейрона p1v1=p2v2
1)скорость молекул, формула: v=корень из (3kt/m0). т.е. скорость молекул зависит от массы молекул и температуры газа. температура не изменяется, масса тоже. значит, скорость не изменилась. ответ д.
2) средняя кинетическая энергия, формула: ek=mv^2/2. масса нашего газа не изменялась, как и скорость, так что кинетическая энергия не менялась. ответ д.
3)по закону клапейрона:
у нас уменьшился объем в 4 раза. значит:
p1*v1=p2*0.25v
обратно пропорциональня зависимоть, давление увеличилось в 4 раза. ответ а.
4)из условия ясно, что объем уменьшился в 4 раза. ответ г.
5) температура по условию не менялась. ответ д.
к дуговой лампе с сопротивлением 5.0 ом последовательно присоединен реостат с сопротивлением 4.5 ом. определить ток в лампе, если напряжение на зажимах генератора 127 в, а проводка выполнена медным проводом длиной 20 м и сечением 1.8 мм в квадрате.
решение
1) определим сопротивление проводки:
удельное сопротивление меди: (ро)(cu)=0,017 ом*мм^2/м
r=(ро)*l/s=0,017*20/1,8=0,19 ом
2) опредлим сопротивление всей цепи:
rобщ=rл+rр+rпр=5,0+4,5+0,19=9,69 ом
закон ома:
i=u/rобщ
где
u — эдс источника тока (в нашем случае напряжение на зажимах генератора), в
rобщ — сопротивление нагрузки, ом
i=127/9,69=13,1 а
3) для последовательного соединения проводников:
iобщ=i1=i2==in
значит ток лампы = току общему = 13,1 а
Ответ разместил: Tewr1
10.03.2019 18:48
мяч 1 секунду летит вверх и 1 секунду вниз, поэтому его вертикальная скорость
vв = g * 1 = 9,8 м/с, а наибольшая высота h = vв² / (2 * g) = 9,8² / (2 * 9,8) =
96,04 / 19,6 = 4,9 м.
m=kit из этой формулы выражаю силу тока и перевожу все величины в си
i=m/kt=0.3 х10(-3)кг/ (0.304 х10(-6)кг/кл х 600с)=1.64а
Другие вопросы по Физике
Можно ли считать земной шар материальной точкой при определении времени восхода солнца на восточной и западной границах россии?…
Расчитайте давление на платформе станции метро, находящейся на глубине 30 м, если на поверхности атмосферное давление равно 101,3кпа…
1). под каким полным давлением нужно подавать дыхательную смесь водолазам, которые работают на дне озера на глубине 13 м? атмосферное давление равно 100 кпа…
Скорость тела равна 60 км/час. чему равна скорость тела в м/с?…
Определите вес воды в бассейне размерами 25м х 4м х 2м. плотность воды 1000 кг/м3…
Какую работу совершает кран при равномерном подъеме стальной объемом 0,4м(3) на высоту 5м? плотность стали равна 7900 кг/м(3)…
Два заряда q и 3q расположены в ваккуме на расстоянии r друг от друга. как и во сколько раз изменится напряженность электростатического поля в точке, лежащей посередине между , есл…
При аварийном торможении автомобиль, движущийся со скоростью 72 км/ч остановился через 5 с. найти тормозной путь и ускорение при торможении…
Нужно решение. 1. определите значение средней кинетической энергии поступательного движения молекул гелия, имеющего при давлении 1000 кпа плотность 0, 12 км / м3 или 2. сколько мо…
Определите показания вольтметра в схемах на рисунке…
Решите номера, кроме 2,3 , можете один , если все не в состоянии….
Какое напряжение нужно приложить к свинцовой проволоке длиной 2 м, чтобы сила тока в проволоке равнялась 2 а? диаметр проволоки 0,6 мм…
Помогите!!! Очень важно! Определите площадь опоры, на которую нужно поставить груз массой 40 кг, чтобы произвести давление 8•105 Па.
1. Вычислить площадь опоры тела и его обьем 2.
Вычислить массу тела 3.
С какой силой давит тело на опору?
4. Какого давление тела на поверхтность?
5. Определить цену деления шкалы динамометра 6.
Чему равна сила трения, если тело движется равномерно, со скоростью указанной на каточке 7.
Вычислить коэффицент трения 8.
Вычислить силу трения при уменьшении силы тяги в 2 раза 9.
Чему равен импульс тела?
10. Вычислить механическую работу силы тяги на пути, указанном на карточке 11.
Вычислить мощность при движении тела 12.
Вычислить кинетическую энергию тела.

На этой странице находится вопрос 1. Вычислить площадь опоры тела и его обьем 2?, относящийся к категории
Физика. По уровню сложности данный вопрос соответствует знаниям
учащихся 5 – 9 классов. Здесь вы найдете правильный ответ, сможете
обсудить и сверить свой вариант ответа с мнениями пользователями сайта. С
помощью автоматического поиска на этой же странице можно найти похожие
вопросы и ответы на них в категории Физика. Если ответы вызывают
сомнение, сформулируйте вопрос иначе. Для этого нажмите кнопку вверху.
3.3.1
Особенности расчетов опор.
В
пособии рассматриваются расчеты бетонных
опор. Бутобетонные опоры и сборно-монолитные
опоры с армированными контурными блоками
(см. п.2.4) рассчитывают как бетонные, при
этом площади контурных блоков включают
в состав сечений опор.
Бетонные
опоры по первой группе предельных
состояний рассчитывают на прочность,
устойчивость формы и устойчивость
положения. Устойчивость формы – это
способности элемента сохранять форму
при действии продольных сил; устойчивостью
положения опоры называют ее способность
не изменять положения при действии на
нее опрокидывающих и сдвигающих сил.
По
второй группе предельных состояний
опоры рассчитывают по трещиностойкости
и по ограничению смещения верха опор.
Для опор с разрезными балочными пролетными
строениями это смещение не должно
превышать
,
см, где l0
– длина меньшего опирающегося на опору
пролетного строения, принимаемая не
менее 25 м.
На
опору в общем случае действует несколько
сил, вызванных различными нагрузками
в разных сочетаниях. Эти силы подразделяют
на вертикальные, продольные горизонтальные,
т.е. направленные вдоль оси моста, и
поперечные горизонтальные, направленные
поперек оси моста.
К
вертикальным силам относят:
–
собственный вес опоры;
–
опорные давления от веса пролетных
строений с учетом веса мостового полотна,
смотровых
приспособлений, противопожарных
обустройств и т.п.;
–
опорные давления, вызываемые временными
нагрузками на пролетном строении;
–
вертикальные силы от горизонтальных
нагрузок, получаемые при переносе этих
нагрузок
в уровень опорных частей;
–
гидростатическое давление.
Горизонтальные
продольные силы могут быть вызваны:
–
торможением подвижного состава (силой
тяги);
–
продольной ветровой нагрузкой, действующей
на пролетное строение;
–
давлением ветра непосредственно на
опору.
Кроме
того, в подвижных опорных частях возникают
силы трения (сопротивления сдвигу).
Поперечные
горизонтальные силы возникают в
результате действия:
–
поперечных ударов подвижного состава;
–
поперечной ветровой нагрузки, действующей
как на пролетное строение, так и
непосредственно
на опору;
–
поперечной ветровой нагрузки, действующей
на подвижной состав.
На
промежуточные опоры, расположенные в
русле реки, может действовать поперечная
горизонтальная сила, вызываемая давлением
льда на опору, а на судоходных реках –
нагрузка от навала судов, которая может
быть направлена как вдоль, так и поперек
оси моста. Эти нагрузки не учитывают
совместно с силой торможения. На кривых
участках пути на опору действует
горизонтальная центробежная сила,
которую не учитывают совместно с
поперечными ударами подвижного состава.
Конкретные сведения о величинах этих
нагрузок и условиях их применения
приведены в нормах проектирования и в
учебном пособии 2.
На
заднюю грань устоя действует давление
грунта от его собственного веса и
горизонтальное давление от временной
нагрузки, которая находится на насыпи
(на призме обрушения).
Все
нагрузки с пролетных строений балочных
систем передаются на опоры через опорные
части, за исключением силы торможения,
передаётся на устой. Принято, что в этом
случае торможение передаются на устой
рельсошпальной решетки, силу торможения
принимают приложенной в уровне головки
рельса.
Опорное
давление по абсолютной величине равно
опорной реакции, действующей на пролетное
строение. При определении опорных
давлений от временных нагрузок на
пролетных строениях используют их линии
влияния, которые аналогичны линиям
влияния опорных реакций.
При
одновременном действии на опору
нескольких временных нагрузок, их
учитывают в расчетах с коэффициентами
сочетаний
.
3.3.2
Назначение основных размеров опор.
Размеры
оголовков опор определяют из условий
размещения опорных частей, установленных
нормами проектирования.
Размер
подферменной плиты вдоль моста может
быть подсчитан по формуле (рис. 3.22):
,
(3.69)
где
с
– расстояние между осями опорных частей,
опирающихся на опору пролетных строений;
a1,
a2
– размеры опорных частей (вдоль оси
моста) левого и правого пролетных
строений; n
– расстояние от края опорной части до
боковой грани подферменника, которое
должно быть не менее 15 см; m
– расстояние от грани подферменника
до края подферменной плиты, назначаемое
с учетом возможности установки домкратов
для подъемки концов пролетных строений;
это расстояние должно быть не менее 15
см при пролетах от 15 до 30 м, 25 см при
пролетах от 30 до 100 м.
Величину
c
подсчитывают по формуле:
, (3.70)
где
Lл,
Lп
– соответственно полная длина левого
и правого пролетных строений; lл,
lп
– расчетный пролет левого и правого
пролетных строений; e
– расстояние между торцами пролетных
строений (для железобетонных пролетных
строений с пролетами до 42 м обычно
принимают e=5
см, при больших пролетах это расстояние
определяют из условия взаимных перемещений
концов пролетных строений, опирающихся
на опору).
Для
неразрезных и консольно-балочных
пролетных строений, когда на опоре вдоль
моста расположена одна опорная часть,
c=0,
a1=a2=a:
(3.71)
Необходимую
ширину подферменной плиты (размер
поперек оси моста) подсчитывают по
формуле:
,
(3.72)
где
B
– расстояние между осями балок пролетного
строения; b
– ширина опорной части (поперек оси
моста); n
– то же, что и в формуле (3.69); m1
– расстояние от грани подферменника
до края подферменной плиты. В двухпутных
мостах ширину подферменной плиты D
увеличивают на расстояние между осями
опирающихся на опору пролетных строений.
Величина
m1
зависит от типа опорных частей и для
прямоугольной в плане подферменной
плиты должна быть не менее: при плоских
и тангенциальных опорных частях 30 см;
при катковых и секторных опорных частях
– 50 см; для плитных пролетных строений
величина m1
должна быть не менее 20 см.
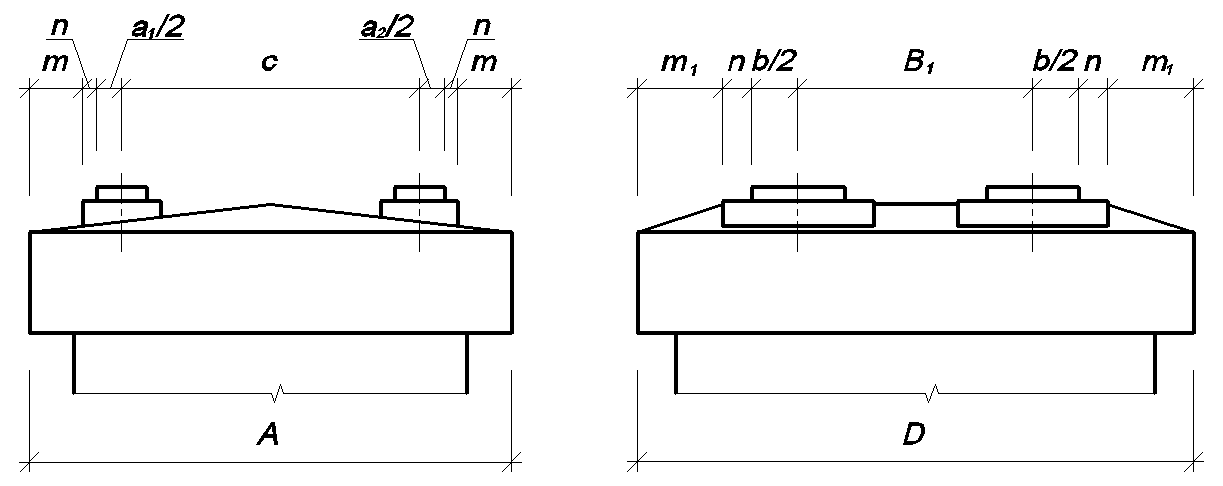
Рис.
3.22. Схемы к определению размеров оголовка
промежуточной опоры
При
закругленной или заостренной форме
подферменной плиты расстояние от угла
подферменника до ближайшей ее грани
должно быть не менее m
(рис. 3.23). Исходя из этого требования,
определяется величина m1.
Если закругление плиты выполнено по
дуге окружности радиуса r,
то часто величину m1
принимают равной этому радиусу.
С
целью обеспечения стока воды с подферменной
плиты, на ней устраивают сливы путем
придания верхней поверхности плиты
уклонов не менее 1:10.
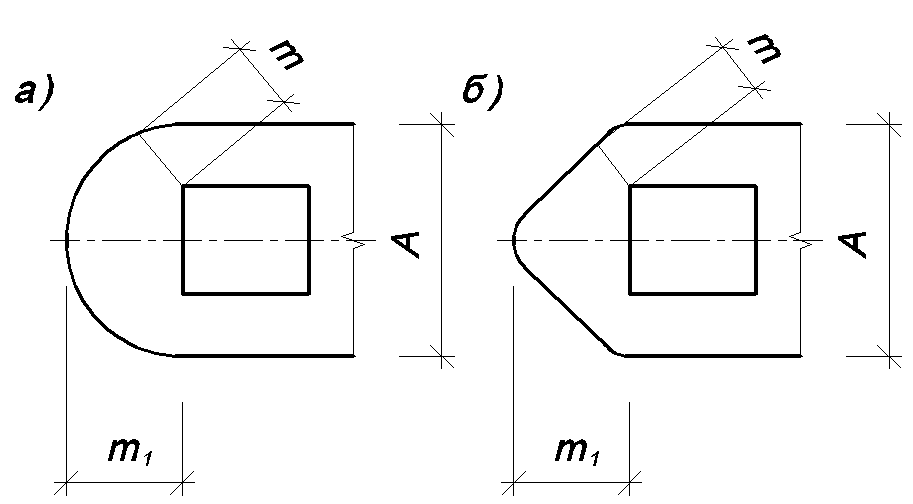
Рис.
3.23. Схемы к определению размеров
подферменной плиты:
а
– при закругленной форме плиты; б – при
заостренной форме плиты
Верх
подферменника должен отстоять от
расчетного уровня высоких вод не менее,
чем на 25 см, а от наивысшего уровня
ледохода – не менее, чем на 50 см.
Подферменник должен возвышаться над
гребнем сливов не менее, чем на 15 см.
Подферменная
плита должна иметь толщину не менее 40
см и иметь свесы над телом опоры не менее
10 см. Для предотвращения увлажнения
поверхностей опоры водой, стекающей с
подферменной плиты, снизу вдоль периметра
ее свесов устраивают небольшие канавки
(слезники).
Размер
подферменной плиты устоя A
(рис. 3.24), измеряемый от шкафной стенки
вдоль оси моста, должен быть не менее
величины, подсчитываемой по формуле:
,
где
L,
l
– соответственно длина и расчетный
пролет пролетного строения, опирающегося
на устой; e
– расстояние
между шкафной стенкой устоя и торцом
пролетного строения; a
– размер опорной части вдоль оси моста;
n
и m
– то же, что и в формуле (3.69). Величину e
принимают из тех же соображений, что и
расстояние между торцами опирающихся
на промежуточную опору пролетных
строений.
Подферменная
плита устоя имеет прямоугольную форму
в плане. Ширина ее назначается так же,
как и для промежуточной опоры, т.е. по
формуле (3.72).
Ширина
массивного устоя B
определится из условия, чтобы подферменная
плита, как и в промежуточных опорах,
имела свесы во все стороны не менее 10
см.
Длину
необсыпных устоев определяют с учетом
следующих указаний норм проектирования.
Уклон конуса насыпи на расстоянии первых
шести метров от бровки земляного полотна
должен быть не круче 1:1,25, на участке
следующих шести метров – не круче 1:1,5,
а в пределах подтопления, т.е. ниже уровня
высоких вод, уклон конуса насыпи должен
быть не круче 1:1,5 (см. рис.2.59). При очень
высоких насыпях (свыше 12,0 м) крутизна
откосов конусов должна определяться
специальным расчетом по устойчивости
насыпи.
Вершина
конуса насыпи должна отстоять от задней
грани устоя на величину
,
которая должна быть не менее 75 см при
высоте насыпи до 6,0 м и не менее 100 см при
высоте насыпи более 6,0 м. В железнодорожных
мостах возвышение подошвы рельсов над
бровкой земляного полотна (над вершиной
конуса насыпи) на дорогах I
и II
категории составляет 90 см, а на дорогах
III
категории – 75 см.
Переднюю
грань необсыпного устоя делают
вертикальной, а задним граням с целью
экономии кладки может придаваться
наклон (см.рис.2.59,а,б)
При
назначении длины обсыпного устоя поверху
должны быть выполнены следующие
требования норм проектирования.
Расстояния от верха подферменника
(опорной площадки) до конуса насыпи
,
измеряемое в плоскости шкафной стенки,
должно быть для железнодорожных мостов
не менее 50 см. Конус насыпи должен иметь
уклон не круче 1:1,5, а при высоте насыпи
свыше 12 м этот уклон должен определяться
расчетом по устойчивости (см. рис. 2.60).
Обсыпные
массивные устои, как правило, снабжаются
железобетонными крыльями, что позволяет
уменьшить массивную часть устоя. Конец
крыла должен заходить в конус насыпи
на величину
.
Необходимые
расстояния от верха подферменников до
конуса насыпи
нормами проектирования установлены из
соображений, чтобы грунт насыпи не
попадал на оголовок опоры, не загрязнял
опорные части. Для защиты опорных частей
от загрязнения иногда устраивают
ограждающие стенки по краям подферменной
плиты (рис. 3.24). При этом указанные выше
расстояния
измеряют не от верха опорной площадки
подферменника, а от верха ограждающей
стенки. Применение ограждающих стенок
сокращает длину устоя.

Рис.
3.24. Схема к определению размеров
подферменной плиты устоев и длины
обсыпных устоев:
а
– при отсутствии ограждающих стенок;
б – при устройстве ограждающих стенок
Передней
грани устоя иногда придают уклон,
приблизительно равный 3:1, а задней грани
– уклон примерно 8:1, хотя заднюю грань
нередко делают и вертикальной (см. рис.
2.60). При этом исходят из того, чтобы
равнодействующая от всех постоянных
нагрузок, включая горизонтальное
давление грунта конуса насыпи, проходила
по возможности ближе к центру тяжести
сечения опоры по обрезу фундамента.
Применение наклонных граней позволяет
сократить объем кладки устоев.
Линия
пересечения поверхности конуса насыпи
с передней гранью устоя должна быть
выше уровня высоких вод не менее, чем
на 0,5 м (см. рис.2.60)
Размеры
промежуточной опоры поверху, вдоль оси
моста (толщина тела опоры) определяются
размерами подферменной плиты с учетом
свесов. Размеры опоры к низу в связи с
увеличением внутренних усилий в ее
сечении, прежде всего изгибающих моментов
относительно оси, перпендикулярной оси
моста, увеличивают, придавая боковым
граням наклон 20:1…40:1 (рис. 2.53,а). Такое
изменение размеров опоры целесообразно
только в том случае, если опора монолитная,
бетонируется в опалубке непосредственно
на объекте, что характерно для мостов
старых проектировок. В настоящее время
применяют чаще всего сборно-монолитные
опоры, в которых в качестве опалубки
используют блоки облицовки. Поэтому
опору делают постоянной толщины по всей
ее высоте или на отдельных участках
(рис. 3.25,б). Конечно, это приводит к
некоторому увеличению объема кладки,
но получается экономия ее стоимости за
счет значительного сокращения типоразмеров
блоков облицовки.
В
поперечном направлении, т.е. перпендикулярно
оси моста, размер опоры (ширина) также
определится размерами подферменной
плиты. Но так как размеры опоры в этом
направлении достаточно большие, а силы,
действующие на мост в поперечном
направлении сравнительно невелики,
увеличивать поперечные размеры опоры
к низу, как правило, нет необходимости.
В
опорах на реках с очень мощным ледоходом
при значительной толщине льда и высокой
его прочности, как было отмечено в п.
2.4, применяют ледорезы. Режущей грани
ледореза придают уклон 1:2…1:1,5. Верх
ледореза должен располагаться выше
наивысшего уровня ледохода не менее,
чем на 1,0 м, а низ ледореза – на расстоянии
не менее 0,5 м ниже наиболее низкого
уровня ледохода с учетом толщины льда
(см. рис. 2.58.) Из этих соображений
определится размер опоры с ледорезом
у обреза фундамента.
Речные
опоры должны иметь обтекаемую форму.
Но при высоких опорах, когда расстояние
от верха опоры до уровня высоких вод
значительно, придавать сечениям опоры
обтекаемую форму по всей ее высоте
нецелесообразно. В этом случае верхняя
часть опоры может иметь прямоугольную
форму или состоять из отдельных бетонных
или железобетонных столбов (см. рис.
2.56). Необходимые размеры этой части
опоры определяются расчетом.
Высоту
тела промежуточной опоры определяет
отметка обреза фундамента.
В путепроводах и в мостах на суходолах
ее назначают на 0,5 м ниже поверхности
грунта, а на водотоках – ниже уровня
меженных вод. Кроме того, из соображений
предохранения фундамента от повреждения
льдом, его обрез назначают ниже поверхности
наинизшего уровня ледостава на толщину
льда, с учетом возможного ее увеличения
у опоры. Это увеличение принимают равным
25 см. Что касается назначения отметки
обреза фундамента у необсыпных устоев,
здесь существует лишь одно ограничение
– чтобы фундамент не выступал над
поверхностью грунта. У обсыпных устоев
обрез фундамента может назначаться
выше поверхности грунта.
3.3.3.
Определение внутренних усилий в сечении
промежуточных опор.
В
расчетах опор внутренние усилия, как
правило, требуется определить в нескольких
сечениях. Поэтому при определении усилий
от собственного веса необходимо
определить вес отдельных элементов
опоры Gi:
оголовка, прокладных рядов, верхней
части опоры, нижней части, имеющей в
речных опорах обтекаемую форму, и т.д.
(рис. 3.25). Вес каждого элемента опоры
определяют с учетом его проектных
размеров и объемного веса материала,
из которого он выполнен (обычно это
бетон, бутобетон или железобетон).
Опорные
давления от собственного веса пролетных
строений, мостового полотна и находящихся
на мосту различных обустройств Vgi
также определяют по их проектным размерам
с учетом объемных весов материалов. Вес
типовых пролетных строений, часто
применяемых в мостах под железную
дорогу, определен соответствующей
технической документацией.
Временная
нагрузка от подвижного состава в общем
случае вызывает действующие на опору
вертикальные силы в виде опорных давлений
Vv,
горизонтальные продольные силы НТ,
возникающие
при торможении, а также горизонтальные
поперечные силы НГС
и вертикальные силы VГС
от ударов подвижного состава. На кривых
участках пути действует центробежная
сила.
Для
определения опорных давлений Vv
применяют линии влияния (рис.3.26,а). Эти
линии влияния могут быть использованы
для определения давлений на опоры от
постоянных нагрузок и от горизонтальных
поперечных временных нагрузок (поперечные
удары подвижного состава, центробежная
сила, поперечная ветровая нагрузка).
Горизонтальная
поперечная сила НГС,
вызываемая ударами подвижного состава,
прикладывается в уровне головки рельса.
На опору она будет передаваться через
опорные части. Поэтому при переносе
силы НГС
в уровень опорных частей необходимо
учесть момент МГС,
равный произведению силы НГС
на расстояние от головки рельса до
центра опорных частей. Момент МГС
будет воспринят парой сил VГС=МГС/В
(В
– расстояние между центрами опорных
частей, измеряемое поперек оси моста).
Силы VГС
можно считать приложенными к верху
подферменников, направлены они в
противоположные стороны.
Поперечная
ветровая нагрузка действует на пролетное
строение и на подвижной состав. Поверхность
пролетного строения, на которую действует
ветер, измеряют от подошвы рельса до
его низа, а рабочую ветровую поверхность
подвижного состава принимают в виде
сплошной полосы высотой 3,0 м с центром
давления на высоте 2,0 м. Силы, вызываемые
ветровой нагрузкой, переносят, как и
силы от поперечных ударов подвижного
состава, в уровень опорных частей.
Продольную
ветровую нагрузку на пролетные строения
со сплошными главными балками принимают
в размере 20% от поперечной нагрузки.
Продольную ветровую нагрузку на подвижной
состав не учитывают.
Давление
ветра непосредственно на опору принято
в виде равномерно распределенной по ее
поверхностям нагрузки. Для удобства
расчетов ее можно заменить сосредоточенными
силами W1…Wn,
действующими как поперек, так и вдоль
оси моста.
Горизонтальную
поперечную нагрузку от центробежной
силы принимают в виде равномерно
распределенной нагрузки интенсивностью
n,
приложенной на расстоянии 2,2 м от головки
рельса. Центробежную силу следует также
переносить в уровень опорных частей.
Сила
торможения (сила тяги) НТ
действует в уровне головки рельса. Но
в соответствии с нормами проектирования
в расчетах промежуточных опор ее можно
принимать в уровне опорных частей, не
учитывая влияния изгибающих моментов,
возникающих при переносе сил.
На
речные опоры действуют силы, вызываемые
давлением льда НЛ,
навалом судов НГС.
При
определении веса частей опор (в том
числе и устоев), находящихся ниже уровня
воды, учитывают гидростатическое
давление GГД.

Рис.
3.25. Силы, действующие на промежуточную
опору железнодорожного моста
Перечисленные
силы, вызываемые временными нагрузками,
действуют на опоры в различных сочетаниях,
которых может быть очень много. При этом
силы учитывают с соответствующими
коэффициентами сочетаний, величины
которых установлены нормами проектирования.
Отметим лишь наиболее характерные
сочетания, учет которых в расчетах чаще
всего определяет несущую способность
и трещиностойкость опоры. При этом не
рассматриваются сочетания нагрузок, в
которые входят центробежная сила
(рассматриваются опоры мостов,
расположенных на прямых участках ж.д.
пути), нагрузка от навала судов, так как
в учебном пособии рассматриваются
расчеты мостов с небольшими пролетами,
при которых судоходство на реке
отсутствует.
Сочетание
1. Оба опирающихся на опору пролетных
строений загружены временной нагрузкой.
При этом, если суммарная длина обоих
пролетных строений не превышает 80 м,
оба пролетных строения загружают
эквивалентной нагрузкой
.
При
,
большее по длине пролетное строение
загружают эквивалентной нагрузкой
,
а второе пролетное строение – вагонной
нагрузкой (рис. 3.26,б). Действуют поперечные
удары подвижного состава. Коэффициенты
сочетаний для всех нагрузок принимают
равными единице.
Сочетание
2. Временную нагрузку принимают такой
же, как и в первом сочетании, но вместо
поперечных ударов подвижного состава
учитывают давление ветра на подвижной
состав, на пролетное строение и на опору.
Ледовую
нагрузку определяют дважды: при наивысшем
уровне ледохода и в начальной стадии
ледохода (при первой подвижке льда). При
этом и давление ветра непосредственно
на опору определяют выше этих уровней.
По нормам проектирования величину
коэффициента сочетаний
принимают равным: для временной
вертикальной нагрузки 0,8; для ветровой
нагрузки 0,5; для давления льда 0,7.
Сочетания
1 и 2 используют при определении
максимальных значений продольных сил
и соответствующих им изгибающих моментов
относительно оси, параллельной оси
моста (оси x–x).
Сочетание
3. Временной нагрузкой загружены оба
пролетных строения. При этом, если
,
пролетные строения загружают эквивалентной
нагрузкой
,
а при
нагрузкой
загружают пролетное строение, опирающееся
на рассматриваемую опору через неподвижные
опорные части; второе пролетное строение
загружают гружеными вагонами. Действуют
сила торможения НТ
и ветровая нагрузка Hw.
Сила торможения в общем случае приложена
на высоте 2,2 м от головки рельса. Но в
мостах с балочными пролетными строениями,
как было ранее отмечено, ее допускается
принимать приложенной в уровне центров
опорных частей, не учитывая при этом
момент от переноса нагрузки. Можно
считать также приложенной в уровне
центров опорных частей и продольную
ветровую нагрузку на пролетные строения
Hw.
Продольное
усилие, передаваемое с подвижных опорных
частей, учитывают только тогда, когда
неподвижные опорные части установлены
со стороны меньшего из примыкающих к
опоре пролетов. В этом случае продольное
усилие принимают равным сумме продольных
усилий, передаваемых через опорные
части обоих пролетных строений, но не
более усилия, передаваемого с наибольшего
пролетного строения при неподвижном
его опирании на рассматриваемую опору.
Усилие, передаваемое с наибольшего
пролетного строения через подвижные
опорные части, равно
, (3.73)
где
– максимальный коэффициент трения в
опорных частях, принимаемый в соответствии
с указаниями СП 35.13330.2011; V
– вертикальное опорное давление от
временной и постоянных нагрузок,
передаваемых на опору через подвижные
опорные части.
Сочетание
4. Временной нагрузкой загружено пролетное
строение, опирающееся на рассматриваемую
опору через неподвижные опорные части.
Действуют продольная сила от торможения
НТ,
передаваемая с этого пролетного строения,
ветровая нагрузка на пролетные строения
и на опору. Продольная горизонтальная
сила может быть уменьшена за счет трения
,
возникающего в подвижных опорных частях
соседнего пролетного строения:
, (3.74)
где
– минимальный коэффициент трения в
подвижных опорных частях; V
– опорное давление, возникающее в
подвижных опорных частях только от
постоянных нагрузок.
Сочетания
3 и 4 рассматривают при определении в
сечениях опоры изгибающих моментов
относительно оси, перпендикулярной оси
моста (оси y–y),
и соответствующих им продольных сил.
Описанные
схемы загружения используют в расчетах
на прочность и устойчивость формы по
первой группе предельных состояний.
В
расчетах по трещиностойкости и по
определению перемещения верха опоры
следует рассматривать такие же схемы
загружения линий влияния временными
нагрузками. Но при этом коэффициенты
надежности по нагрузке к временным
нагрузкам принимают равными единицы.
Из
приведенных схем загружения для проверки
прочности (трещиностойкости) сечений
выбирают те схемы, которые дают наиболее
неблагоприятные для работы опоры
сочетания. Обычно при этом отдельно
рассматривают сочетания нагрузок, в
которых горизонтальные силы направлены
поперек оси моста, и отдельно с
горизонтальными силами, направленными
вдоль моста.
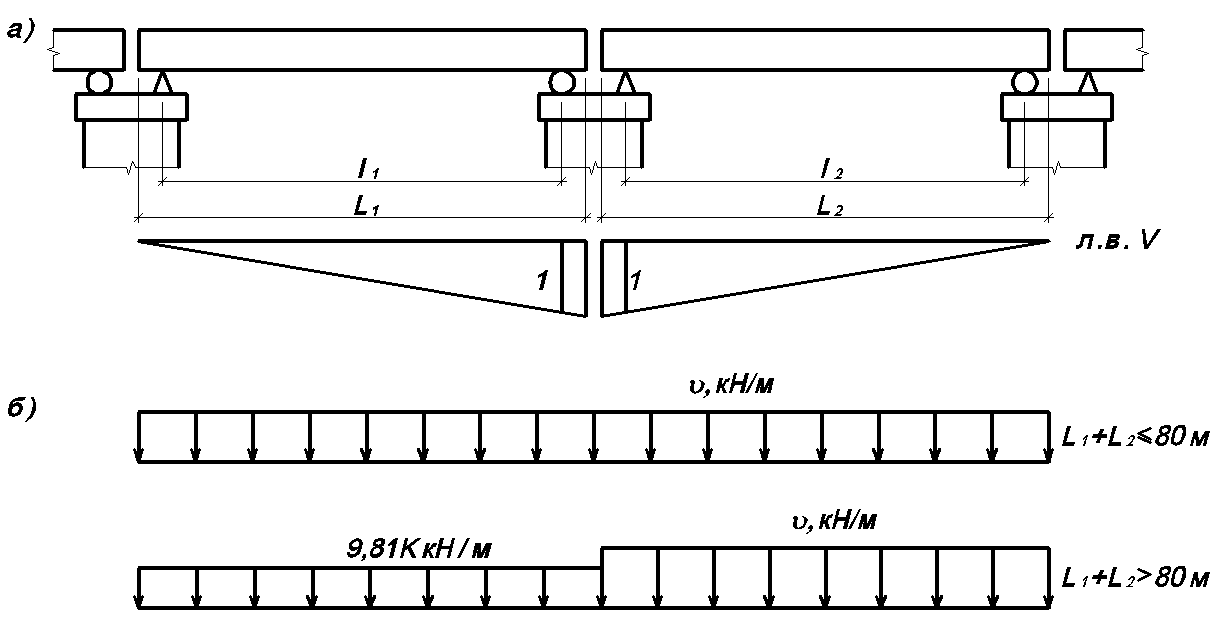
Рис.
3.26. Схемы к определению опорных давлений
на промежуточные опоры моста:
а
– расчетная схема и линии влияния; б –
загружения линий влияния временной
нагрузкой от подвижного состава в
расчетах по прочности, устойчивости
формы, по трещиностойкости
Внутренние
силы – продольную силу N
и изгибающие моменты Mx
и My,
определяют
в наиболее характерных сечениях опоры:
по обрезу фундамента и в местах изменения
размеров сечения. Моменты определяют
относительно осей, проходящих через
центры тяжести рассматриваемых сечений,
которые могут иметь несимметричную
форму.
(3.75)
В
формулах (3.75) прописными буквами
обозначены действующие на опору силы
в соответствии с рис. 3.25, а строчными –
расстояния от соответствующей силы до
оси x–x
для момента Mx
и расстояния от сил до оси y–y
для момента My;
B
– расстояние между центрами опорных
частей, измеряемое в поперечном
направлении;
– расстояние от опорных давлений Vg
и Vv
до оси y–y
(
или
на рис. 3.25).
При
определении момента Mx
силу НЛ
и соответствующие ей расстояния hЛ
подсчитывают дважды: при первой подвижке
льда и при наивысшем уровне ледохода.
Соответственно и гидростатическое
давление GГД
определяют для этих уровней.
В
двухпутных мостах вертикальные опорные
давления Vg
и Vv
могут создавать изгибающие моменты
относительно оси x–x
как при загружении одного пролетного
строения, так и обоих, даже при симметричной
форме сечения относительно продольной
оси моста. При загружении двух путей
это связано с тем, что коэффициенты к
временной нагрузке s1
и
,
а для постоянных нагрузок коэффициент
для одного из пролетных строений
принимают равным единице, а для второго
пути в соответствии с нормами проектирования
их можно принимать меньшими единицы.
3.3.4.
Определение внутренних усилий в сечениях
устоев.
На
устои действуют вертикальные и
горизонтальные продольные силы.
Горизонтальные поперечные силы в
расчетах устоев не учитывают, так как
значительная часть устоя находится в
грунте насыпи.
При
определении внутренних усилий в сечениях
устоев необходимо учитывать действие
следующих вертикальных сил (рис. 3.27):
–
собственный вес опоры;
–
опорное давление Vg
от веса пролетного строения с элементами
мостового полотна с учетом имеющихся
на нем приспособлений и обустройств
(смотровых приспособлений, осветительных
устройств, различных коммуникаций и
т.п.);
–
вертикальное опорное давление Vv
от временных нагрузок, находящихся на
пролетном строении;
–
временную нагрузку, находящуюся на
устое, Vvy;
–
вертикальное давление Gg
от собственного веса грунта.
На
устои действуют горизонтальные силы:
–
продольная сила, вызываемая торможением
подвижного состава, Т;
–
продольная сила от ветровой нагрузки,
действующей на пролетное строение, W;
–
боковое давление phgx
от собственного веса грунта;
–
боковое давление phqx
от временной нагрузки, находящейся на
насыпи.
Для
определения внутренних усилий в массивном
устое от собственного веса его разбивают
на отдельные блоки по возможности
простой формы и определяют вес каждого
блока (см. рис. 3.27). Так как расчет устоя
связан с определением изгибающих
моментов в его характерных сечениях,
необходимо определить расстояние от
каждой составляющей веса устоя силы Gi
до вертикальной линии, проходящей через
центр тяжести рассматриваемого сечения,
а в расчетах на опрокидывание – расстояние
от линии действия каждой силы Gi
до оси, относительно которой определяют
опрокидывающий и удерживающий моменты.
Горизонтальное
(боковое) давление грунта на единицу
площади задней грани устоя от его
собственного веса определяют по формуле:
, (3.76)
где hx
– высота засыпки, измеряемая от подошвы
рельса до рассматриваемого сечения, м;
– нормативный удельный вес грунта, кН/м3;
– коэффициент
нормативного бокового давления грунта
засыпки устоев, определяемый по формуле:
,
(3.76,а)
где
n
– нормативный угол внутреннего трения,
град.
Значения
и
n
должны назначаться на основании
лабораторных испытаний грунта,
предназначенного для засыпки устоев.
Устои следует засыпать дренирующим
грунтом, для которого можно принять
и
n=350.
Давление
грунта на заднюю грань устоя изменяется
по линейному закону. Оно может быть
представлено в виде сосредоточенной
силы Fhg,
определяемой по формуле:
, (3.77)
где
–
давление грунта на единицу площади
сечения у образа фундамента,
b
– ширина устоя; h
– высота устоя.
Задняя
грань устоя может иметь наклон (рис.
3.28). В этом случае давление Fhg
считают приложенным к вертикальной
плоскости AB,
которую можно рассматривать как условную
(фиктивную) заднюю грань устоя. Силами
трения, возникающими между кладкой
устоя и грунтом конуса насыпи, как и
между частицами грунта по плоскости
AB,
пренебрегают. Вес призмы грунта ABC
по рис. 3.29 учитывают как постоянную
нагрузку при расчете сечения по обрезу
фундамента, а вес призмы
– как дополнительную постоянную нагрузку
на фундамент.
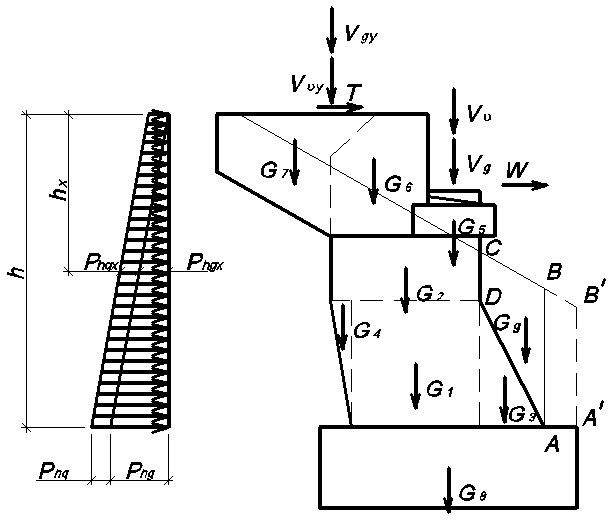
Рис.
3.27. Силы, действующие на массивный устой
железнодорожного моста

Рис.
3.28. Схема к определению давления грунта
от собственного веса на наклонную заднюю
грань тела устоя
Горизонтальное
давление грунта на обсыпной устой со
стороны пролета можно учитывать лишь
в том случае, когда проектом предусмотрены
специальные меры, гарантирующие
стабильность этого давления при
строительстве и эксплуатации моста.
На
заднюю грань устоя действуют также
горизонтальная распределенная нагрузка
Phqx,,
вызываемая подвижным составом, находящимся
на призме обрушения. На рис. 3.27 нагрузка
Phqx
условно показана как равномерно
распределенная. Фактическое её
распределение показано на рис.3.30,а.
При
опирании на устой разрезного балочного
пролетного строения (рис. 3.29,а) для
определения усилий в расчетах по
прочности и трещиностойкости загружения
его нагрузкой СК производят по схемам,
приведенным на рис. 3.29,б с пояснениями,
приведенными в табл.3.1. Длину загружения
призмы обрушения
принимают равной половине расстояния
от подошвы шпал до рассматриваемого
сечения. Эквивалентную нагрузку,
находящуюся на призме обрушения,
определяют при положении вершины линии
влияния
.
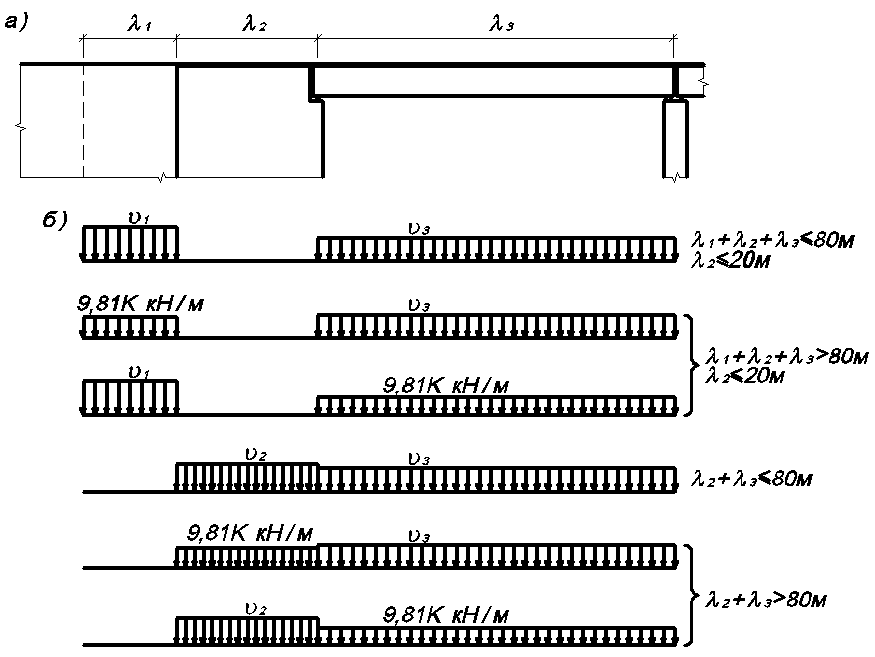
Рис.
3.29. Загружения железнодорожного моста
разрезной балочной системы при расчетах
устоя:
а
– схема моста; б – расположение подвижного
состава в расчетах по прочности,
устойчивости формы, на трещиностойкость
Таблица
3.1
Временные
вертикальные нагрузки при загружениях
устоя по схеме рис.3.29
|
Загружаемая |
Длина |
Ограничение |
Принимаемое |
Нагрузка, |
|
Призма Устой Пролетное |
|
|
0,5 – 0 |
0 v3 |
|
Призма Устой Пролетное |
|
– – 0 |
0 v3 |
|
|
Призма Устой Пролетное |
0,5 – – |
v1 0
|
||
|
Устой Пролетное |
|
|
0,5 0 |
v3 |
|
Устой Пролетное |
|
– 0 |
v3 |
|
|
Устой Пролетное |
0,5 – |
v2 |
Примечание.
Если при езде на балласте
,
принимают
независимо от положения вершины линии
влияния.
Коэффициент
надежности по нагрузке определяют при
длине загружения, равной сумме длин
участков, на которых находится
эквивалентная нагрузка или нагрузка
от груженых вагонов.
Продольную
горизонтальную нагрузку от торможения
(силы тяги) принимают в размере 10% от
веса временной эквивалентной нагрузки,
находящейся на пролетном строении и на
устое; силу торможения от временной
нагрузки на призме обрушения не учитывают.
В отличие от промежуточных опор в
расчетах устоев считают, что сила
торможения передается на устой не через
опорные части как было указано раньше,
а через верхнее строение пути. Поэтому
силу торможения считают приложенной в
уровне головки рельса. При этом, как и
в расчетах промежуточных опор, при двух
железнодорожных путях силу торможения
принимают с одного пути, а при трех и
более путях – с двух путей с учетом
коэффициента s1
(см. п.3.1.3).
Силу
торможения, передающуюся на устой,
учитывают только с участков, загружаемых
эквивалентной нагрузкой. Продольная
ветровая нагрузка передается на устой
через неподвижные опорные части.
При
определении горизонтального давления
грунта на заднюю грань однопутного
устоя от временной нагрузки на насыпи
приняты такие допущения:
под
шпалами, т.е. на длине 2,7 м, временная
нагрузка распределена равномерно,
при
этом давление на единицу площади, кПа:
. (3.78)
В
теле насыпи горизонтальное давление
грунта, вызываемое временной нагрузкой
на
призме обрушения, распределяется под
углом
к вертикали (рис. 3.31).
Эпюра
распределения давления на заднюю грань
устоя при постоянной его ширине b
имеет вид, показанный на рис. 3.31,а. В
верхней части устоя эпюра имеет участок
высотой h1
с постоянной ординатой, так как ширина
распределения вертикального давления
bvx
на этом участке меньше ширины устоя b
и горизонтальное давление на этот
участок передается полностью.
Равнодействующую этого давления Fv1
подсчитывают по формуле:
, (3.79)
где
– коэффициент нормативного бокового
давления грунта, определяемый по формуле
3.76,а.
На
глубине hx,
большей h1,
ширина распределения давления, м
превышает
ширину устоя b
и на устой передается лишь часть
горизонтального давления грунта. Эпюра
давления на устой получает криволинейное
очертание. Равнодействующую этого
давления подсчитывают по формуле:
.
(3.80)
Расстояние
z1
и z2
(см. рис. 3.30) от линии действия сил Fv1
и Fv2
до рассматриваемого сечения устоя
определяют по формулам:
,
(3.81)
,
(3.82)
Значения
коэффициентов
и
принимают в зависимости от величины h,
а коэффициенты
и
– в зависимости от h1
по рис. 3.31, либо по таблице, приведенной
в СП 35.13330.2011.
В
двухпутных устоях при загружении одного
пути распределенное давление на устой
заменяют сосредоточенными силами
(рис. 3.30,б), подсчитываемыми по формулам:
(3.83)
В
этих формулах: h1,
h2
– расстояния, измеряемые от подошвы
шпалы до концов участков, в пределах
которых площадь давления на устой имеет
переменную ширину; b,
b1
– соответственно расстояния от оси
пути до ближайшей и до наиболее удаленной
боковой грани устоя.
Расстояния
от линии действия сил Fv1
и Fv2
до рассматриваемого сечения определяют
как в однопутном устое, а от линии
действия сил Fv3
и Fv4
подсчитывают по формулам:
, (3.84)
, (3.85)
Значения
коэффициентов
и
принимают в зависимости от h2,
также по графику (рис. 3.31), либо по таблице
в СП 35.13330.2011.
При
невысоких устоях расстояние h2
может оказаться больше высоты устоя h
(рис. 3.30, б). В этом случае принимают
Fv4=0,
а силу Fv3
подсчитывают по формуле:
, (3.86)
При
загружении временной нагрузкой обоих
путей, нагрузку от подвижного состава,
как вертикальную, так и горизонтальную,
учитывают с коэффициентом s1.
В
расчетах массивных устоев необходимо
определить продольную силу и изгибающий
момент, приложенные в центре тяжести
сечения по обрезу фундамента. Поскольку
на устой действуют горизонтальные силы
только в продольном направлении,
изгибающий момент определяют относительно
оси, перпендикулярной оси моста (оси
y–y).
При этом необходимо рассмотреть два
расчетных случая: когда горизонтальные
силы направлены в сторону пролета и
когда они направлены в сторону насыпи.

Рис.
3.30. Схемы к определению горизонтального
давления на устой от подвижного состава
на призме обрушения:
а
– для однопутного устоя; б – для
двухпутного устоя

Рис.
3.31. График для определения коэффициентов
,
Первому
случаю соответствуют три первые схемы
загружения вертикальной временной
нагрузкой, приведенные на рис. 3.29,б. При
этих загружениях возникают опорное
давление Vv
и горизонтальные силы Fv,
действующие на заднюю грань устоя (см.
рис. 3.30). Силы Fv
подсчитывают по формулам (3.79, 3.80) или
(3.83). Значение входящей в эти формулы
величины pv
определяют по формуле (3.78), принимая в
ней нагрузку v,
равную эквивалентной при длине загружения
и
,
но не более 19,62 К кН/м; если же на призме
обрушения находится вагонная нагрузка,
принимают v=9,81
К кН/м.
При
расположении на устое неподвижных
опорных частей учитывают силу торможения,
но принимают ее, как было указано ранее,
не в уровне опорных частей, а в уровне
головки рельса. При этом учитывается и
действие ветровой нагрузки на пролетное
строение, передающейся на устой через
неподвижные опорные части. При подвижных
опорных частях учитывают возникающие
в них силы трения, величину которых
определяют по формулам (3.73 или 3.74) с
учетом типа опорных частей.
Горизонтальную
постоянную нагрузку от собственного
веса грунта принимают в виде сосредоточенной
силы Fhg,
подсчитываемой по формуле (3.77).
Случаю,
когда горизонтальные силы, вызываемые
временными нагрузками, действуют в
сторону насыпи, для разрезных балочных
пролетных строений соответствуют три
последние схемы, приведенные на рис.
3.32,б. Нагрузки от подвижного состава на
устое (вертикальную силу и силу торможения)
учитывают в том случае, если они создают
момент того же знака, что и тормозная
сила на пролетном строении, направленная
в сторону насыпи.
Следует
иметь в виду, что в расчетах на прочность
и устойчивость формы коэффициенты
надежности по нагрузке
для постоянных нагрузок для первого и
второго случая загружения будут иметь
разные значения. Если конкретная
постоянная нагрузка создает момент
относительно центра тяжести рассматриваемого
сечения того же знака, что и момент,
вызываемый временными горизонтальными
нагрузками, принимают
;
если эти моменты имеют разные знаки,
3.3.5.
Проверка прочности, устойчивости формы
и трещиностойкости бетонных опор.
Опора
моста с позиций строительной механики
представляет собой стержень, сжимаемый
продольной силой. При этом стержень
всегда считается сжатым внецентренно,
так как учитывается случайный
эксцентриситет
,
по СП 35.13330.2011 принимаемый равным:
где
l0
– расчетная (свободная) длина элемента.
Расчетная
(свободная) длина сжатого элемента
зависит от способов закрепления его
концов. На рис. 3.32 приведены возможные
схемы закрепления концов стержня и
соответствующие этим схемам расчетные
(свободные) длины. Работа сжатых элементов
опор, строго говоря, не соответствует
ни одной из показанных на рисунке схем.
Ориентироваться нужно на такую схему,
которая наиболее бы приближалась к
фактической работе опоры. По нормам
проектирования при применении опорных
частей каткового и секторного типа
взаимную связь соседних опор не учитывают
и расчетную длину l0
принимают равной двум высотам опорам.
Это является допущением: в опорных
частях возникают силы трения, поэтому
какая-то связь между соседними опорами
существует всегда. Такое же допущение
можно принять и при тангенциальных и
плоских опорных частях, хотя в этом
случае оно является более грубым. Неучет
сил трения в опорных частях мало
сказывается на определении расчетной
(свободной) длины опоры, тем более, что
получаемые при этом результаты расчетов
идут в запас прочности. Таким образом,
за расчетную схему опоры принимают
стержень с жестко заделанным концом
внизу и со свободным верхним концом.
Высоту опоры в приводимых ниже расчетах
по устойчивости формы измеряют от точки
приложения к опоре опорных давлений,
т.е. от верха подферменников до обреза
фундамента.

Рис.
3.32. Зависимость расчетной (свободной)
длины стрежня от способа закрепления
его концов
Расчетный
эксцентриситет
определяют как сумму эксцентриситетов,
определимых из статического расчета
и случайного
,
т.е.
Если
по результатам статического расчета в
сечении получены изгибающий момент M
и продольная сила N,
приложенные в его центре тяжести, такое
сечение считают внецентренно сжатым
силой N,
с эксцентриситетом
относительно оси, проходящей через
центр тяжести сечения.
При
действии внецентренно приложенной силы
N
верх опоры получит некоторые отклонения
от первоначального положения (рис.
3.33). Нормы проектирования допускают
упрощенный учет влияния прогиба на
прочность сечения путем умножения
эксцентриситета
на коэффициент
,
подсчитываемый по формуле:
,
где
Ncr
– условная критическая сила, при
достижении которой прямолинейная форма
стержня перестает быть устойчивой.

Рис.
3.33. Изменение эксцентриситета силы при
внецентренном сжатии
В
массивных опорах отклонение их верха
в рассматриваемых случаях незначительно,
поэтому величина коэффициента
близка к единице.
Величину
критической силы Ncr
подсчитывают по формуле:
где
Eb
– модуль упругости бетона; Jb
– момент инерции сечения;
– коэффициент, учитывающий влияние
длительно действующей нагрузки на
прогиб элемента;
–
отношение расчетного эксцентриситета
к высоте сечения h,
но не менее величины
,
подсчитываемый по формуле:
Величину
коэффициента
подсчитывают по формуле:
где Ml
– момент, равный произведению силы Nl
от постоянных нагрузок на расстояние
от линии действия силы Nl
до наименее сжатой грани сечения; M
– то же от постоянных и временных
нагрузок.
Для
невысоких массивных опор критическая
сила может быть подсчитана по приближенной
формуле:
Вводится
ограничение положения силы N:
, (3.87)
где
ac
– расстояние от оси, проходящей через
центр тяжести всего сечения, до наиболее
сжатой грани.
Условие
(3.87) должно исключить скол бетона, если
сила N
проходит достаточно близко к краю
сечения у сжатой его грани. При невыполнении
этого условия размеры сечения должны
быть увеличены.
Условие
прочности и устойчивости формы в общем
виде:
,
где
N
– действующая в сечении продольная
сила; Nпред
– продольная сила, которую может
воспринять сечение.
Внецентренно
сжатые бетонные элементы проверяют на
прочность, когда продольная сила N
выходит за пределы ядра сечения, т.е.
когда
.
Границы ядра сечения определяют по
формуле:
,
где Jb,
Ab
– соответственно
момент инерции и площадь сечения; y
– расстояние
от центра тяжести сечения до его верха
(или низа).
При
проверке сечения на прочность, условие
принимает вид:
,
(3.88)
где
– площадь сжатой зоны сечения.
В
расчетах по проверке прочности сечения
приняты следующие допущения:
–
бетон растянутой зоны полностью
выключился из работы сечения;
–
напряжения в сжатой зоне сечения
одинаковы по всей ее площади и равны
расчетному сопротивлению бетона Rb;
–
равнодействующая усилий от внешних
нагрузок N
приложена в центре тяжести сжатой зоны
сечения.
Для
элемента таврового сечения высотой h
с толщиной полки
при эксцентриситете силы N
в сторону полки (рис. 3.34,а), условие (3.88)
принимает вид:
, (3.89)
где
– соответственно ширина ребра и ширина
полки;
– толщина полки; x
– высота
сжатой зоны.
Расстояние
а
от линии действия силы N
до сжатой грани равно:
При
граница сжатой зоны проходит в пределах
ребра.
(3.90)
При
(граница сжатой зоны проходит в
плите)
принимают в формулах b=bf,
т.е. сечение рассчитывают как прямоугольное
шириной
.
Для
случая, когда эксцентриситет силы N
направлен в сторону ребра (рис. 3.34,б),
условие прочности принимает вид:
, (3.91)
а
граница сжатой зоны x
может быть подсчитана по формуле:
(3.91,а)
где
d=h–
.
При
следует принять bf=b,
при
этом х=2а
и сечение рассчитывают как прямоугольное
шириной b.
Формулы
(3.90), (3.91,а) могут быть приведены к такому
виду:
при
эксцентриситете в сторону полки (в таком
виде формула приведена в СП 35.13330.2011);
при
эксцентриситете в сторону ребра.
Для
элементов прямоугольного сечения
шириной b
в формулах (3.89) и (3.90) следует принимать
и
.
Условие прочности принимает вид:
, (3.92)
при
этом
.

Рис.
3.34. Схемы к расчету бетонного сечения
тавровой формы по прочности:
а
– эксцентриситет сжимающей силы
направлен в сторону полки; б –
эксцентриситет сжимающей силы направлен
в сторону полки
У
опор, расположенных в пределах водотока,
поперечное сечение принимают обтекаемой
формы с заострением или закруглением
в носовой и кормовой части (рис. 3.35). Для
приближенных расчетов такие сечения
можно заменить условным сечением
прямоугольной формы с той же шириной
b,
площадь которого равна площади
фактического сечения. Более точно расчет
таких опор может быть выполнен по
рекомендациям, приведенным в учебном
пособии 2.

Рис.
3.35. Замена фактического сечения опоры
условным:
1
– фактическое сечение; 2 –сечение,
вводимое в расчеты условий прочности
и устойчивости формы
Если
продольная сила не выходит за пределы
ядра сечения (
),
сечение проверяют как на прочность, так
и на устойчивость формы. Проверку
прочности делают по приведенным выше
рекомендациям, т.е. как и для случая,
когда ec>r.
Проверка
устойчивости формы сводится к выполнению
условия:
, (3.93)
где N
– продольная сила, определенная для
расчета по прочности; Rb
– расчетное сопротивление бетона на
осевое сжатие, Ab
– общая площадь всего рассматриваемого
сечения опоры; φ – коэффициент продольного
изгиба, принимаемый по СП 35.13330.2011.
Трещиностойкость
бетонных конструкций опор обеспечивается
ограничением сжимающих напряжений в
бетоне – это расчет по образованию
продольных трещин. Такой расчет выполняют
только для стадии эксплуатации. Условие
трещиностойкости:
, (3.94)
где
– расчетное сопротивление бетона для
расчетов по предотвращению образования
в конструкции продольных трещин на
стадии эксплуатации.
Если
равнодействующая внецентренно сжимающих
сил N
проходит в пределах ядра сечения, то
сжимающие напряжения в сечении определяют
по известной формуле сопротивления
упругих материалов:
, (3.95)
где Ab,
Jb
– соответственно площадь и момент
инерции сечения; ec
– расстояние от линии действия силы N
до центра тяжести сечения; х
– расстояние от центра тяжести сечения
до наиболее напряженной грани элемента.
Если
сила N
выходит за пределы ядра сечения, при
определении
,
принимают следующие допущения (рис.3.36):
-
сжатый
бетон работает упруго, справедлива
гипотеза плоских сечений; -
растянутый
бетон полностью выключился из работы
сечения.
Для
элементов прямоугольного сечения
шириной b,
если сила N
приложена на расстоянии а
от сжатой грани опоры:
,
(3.95,а)
где
x=3а
– высота сжатой зоны.
Рекомендации
для определения
в элементах таврового сечения, когда
ec>r,
приведены в учебном пособии
2 .
Силу
N
в формулах (3.95), (3.95,а) определяют как для
расчетов по второй группе предельных
состояний.

Рис.
3.36. Схема к расчету бетонных опор по
трещиностойкости
3.3.6.
Проверки устойчивости положения.
Под
действием горизонтальных сил опора с
фундаментом мелкого заложения может
потерять устойчивость, т.е. опрокинуться
относительно оси возможного поворота
или переместиться по направлению
действия горизонтальных сил.
Устойчивость
опоры против опрокидывания будет
обеспечена, если выполняется условие:
, (3.96)
где
Mu,
Mz
– соответственно моменты опрокидывающих
и удерживающих сил относительно осей
возможного поворота (опрокидывания),
т.е. относительно осей, проходящих через
точки O1
(рис. 3.37); m
– коэффициент условий работы, принимаемый
равным при фундаментах на скальных
основаниях 0,9, на нескальных – 0,8;
– коэффициент надежности по назначению,
принимаемый равным 1,1 при расчетах в
стадии постоянной эксплуатации и 1,0 при
расчетах в стадии строительства.
Устойчивость
положения против сдвига (скольжения)
будет обеспечена при выполнении условия:
, (3.97)
где
Qr
– сдвигающая сила, равная сумме проекций
сдвигающих сил на направление возможного
сдвига; Qz
– удерживающая сила, равная сумме
проекций удерживающих сил на направление
возможного сдвига; m=0,9
– коэффициент условий работы;
– коэффициент надежности по назначению
(значения его те же, что и при расчете
на опрокидывание).
Удерживающую
силу Qz
подсчитывают по формуле:
где
N
– сумма вертикальных проекций всех
действующих на опору сил в сечении по
подошве фундамента; f
– коэффициент трения, принимаемый
равным:
-
для
скальных грунтов с омыливающейся
поверхностью (глинистые известняки,
сланцы и т.п.) и глин во влажном
состоянии……………………………… 0,25 -
то
же, в сухом состоянии…………………………
……………………………0,30 -
для
суглинков и супесей………………………………………………
………..0,30 -
для
песков…………………………………………………………………………0,40 -
для
гравелистых и галечниковых грунтов………………………
…………… 0,50 -
для
скальных грунтов с неомыливающейся
поверхностью…… …………..0,60
Обычно
бетонные опоры сооружают так: сначала
бетонируют фундамент и после набора
бетоном фундамента необходимой прочности
бетонируют тело опоры. При этом сцепление
между поверхностями фундамента и телом
опоры может оказаться недостаточным.
Поэтому необходимо сделать проверку
по устойчивости положения тела опоры:
на опрокидывание относительно оси,
проходящей через точки O
(см. рис. 3.37), и на сдвиг опоры по верхней
поверхности фундамента. В последнем
случае коэффициент трения бетонной
кладки тела опоры по бетону фундамента
принимают равным 0,55.
Проверки
на устойчивость положения следует также
выполнять для сечений, в которых
изменяются поперечные размеры опоры.
В
расчетах устоев, как на опрокидывание,
так и на сдвиг, учитывают вертикальное
давление грунта в границах abcda
при проверках устойчивости по обрезу
фундамента, в границах abcefa
и klmk
– при проверках по подошве фундамента
(см. рис. 3.37,б). В качестве горизонтальной
удерживающей силы, создаваемой грунтом,
допускается учитывать силу, величина
которой не превышает активного давления
грунта.

Рис.
3.37. Схемы к расчету опор на устойчивость
положения:
а
– для промежуточной опоры; б – для устоя
Потеря
устойчивости положения относится к
первой группе предельных состояний,
при этом действующие на опору силы
определяют от расчетных нагрузок.
Опрокидывающие и сдвигающие силы
принимают с коэффициентом надежности
по нагрузке
,
большим единицы. Удерживающие силы,
вызываемые постоянными нагрузками,
принимают с коэффициентами надежности
по нагрузке
,
меньшими единицы, а для временных
вертикальных нагрузок в этом случае
.
В соответствующих случаях необходимо
учитывать уменьшение веса конструкции
вследствие взвешивающего действия
воды. При определении действующих на
опоры сил необходимо также учитывать
коэффициенты сочетаний нагрузок.
Контрольные
вопросы к.п.3.3
-
По
каким предельным состояниям рассчитывают
бетонные опоры? -
Что
понимается под устойчивостью формы и
устойчивостью положения? -
Какие
силы действуют на опоры? -
Из
каких условий определяют размеры
оголовков опор? -
Как
назначают длины необсыпных и обсыпных
устоев? -
Из
каких соображений может быть назначено
расстояние от грани подферменника до
грани подферменной плиты? От чего
зависят установленные нормами
проектирования минимальные величины
этих расстояний? -
С
какой целью придаются уклоны передней
и задней поверхностям устоя? -
Как
назначают отметки обрезов фундаментов? -
Как
подсчитывают собственный вес опор? -
Как
учитывают продольную ветровую нагрузку,
действующую на пролетные строения, при
расчетах опор? -
Из
каких соображений установлено минимально
допустимое расстояние от верха
подферменника до конуса насыпи в
обсыпных устоях, измеряемое в плоскости
шкафной стенки? Чему оно равно для
железнодорожных мостов? -
Какие
схемы нагружения следует рассматривать
при расчетах промежуточных опор? -
Когда
и как учитывают силы трения, возникающие
в подвижных опорных частях? -
В
каких уровнях, по нормам проектирования,
прикладывают силу торможения в расчетах
промежуточных опор и в расчетах устоев? -
Почему
горизонтальные поперечные нагрузки
вызывают действующие на опоры вертикальные
силы? Как определяют их величину? -
Какие
внутренние усилия и в каких сечениях
необходимо определять при расчетах
промежуточных опор? -
Какие
силы необходимо учитывать при расчетах
устоев? Почему в этих расчетах обычно
не учитывают горизонтальные поперечные
силы? -
Как
подсчитывают горизонтальное (боковое)
давление грунта на заднюю грань устоя? -
В
каких случаях можно учитывать давление
грунта на обсыпной устой со стороны
пролета? -
Какие
схемы загружения временной нагрузкой
пролетного строения, устоя и призмы
обрушения предусмотрены нормами
проектирования? Какой длины при этом
принимают призму обрушения? Как
определяется величина эквивалентной
нагрузки, располагаемой на призме
обрушения? -
Как
определяется давление на устой,
вызываемое временной нагрузкой,
находящейся на насыпи? -
Почему
и в каких случаях коэффициент надежности
к постоянным нагрузкам принимают
меньшим единицы? -
Почему
в расчетах сжатые элементы всегда
рассматриваются как внецентренно
сжатые? -
Как
назначают расчетную высоту опоры в
расчетах по устойчивости формы? -
Как
учитывают прогиб опоры в расчетах по
прочности? -
Как
записываются условия прочности опоры
в общем виде по методу предельных
состояний? -
Какие
условия приняты при определении сжатой
зоны сечения бетонной опоры в расчетах
по прочности? -
В
каких случаях проверку опоры делают
по прочности и по устойчивости формы,
а в каких только по прочности? -
К
какому условию сводится проверка
бетонных опор по трещиностойкости? -
Выполнением
каких условий обеспечивается устойчивость
опоры против опрокидывания и сдвига? -
Почему
необходима проверка на сдвиг тела опоры
по поверхности фундамента? Как выполняется
эта проверка? -
Одинаковой
ли будет устойчивость опоры, когда её
часть находится в воде и когда она
полностью находится не в воде (например,
в путепроводах и виадуках)?
Приложение
А
Схематическая
карта глубин промерзания грунтов

Примечания
-
Карта
не распространяется на горные районы -
Для
супесей и песков мелких и пылеватых
глубина промерзания указанная на карте
должна увеличиваться на 20%.
Приложение
Б

Кривошеев, Юрий Васильевич
Юрий Васильевич Кривошеев (белор. Юрый Васільевіч Крывашэеў) — белорусский государственный деятель, исполняющий

Trigonopterus discoidalis
Trigonopterus discoidalis (лат.) — вид жуков-долгоносиков рода Trigonopterus из подсемейства Cryptorhynchinae

Щитоносный скат
Щитоносный скат (лат. Bathyraja parmifera) — вид скатов рода глубоководных семейства Arhynchobatidae. Обитают в
Кумыш (Карачаево-Черкесия)
Кумыш (карач.-балк. Къумуш) — аул в Карачаевском районе Республики Карачаево-Черкесия. Образует муниципальное

Гормизд (папа римский)
Гормизд (лат. Hormisdas PP.; ? — 6 августа 523) — Папа Римский с 20 июля 514 года по 6 августа 523 года. Занимал

Перес, Неуэн
Патрисио Неуэн Перес (исп. Patricio Nehuén Pérez; род. 24 июня 2000, Урлингам[d], Буэнос-Айрес) — аргентинский

Леопольдия
Леопольдия (лат. Leopoldia) — род многолетних травянистых луковичных растений подсемейства Пролесковые семейства

Ты супер!
«Ты супер!» — международный музыкальный проект НТВ, в котором принимают участие дети, оставшиеся без попечения

История и особенности эля
Эль отличается своим сладким вкусом и пользуется популярностью у любителей пенных напитков. Продукт не проходит
Расчет тела опоры
|
Массивную на всю высоту опору, не имеющую резких изменений контура в плане, рассчитывают в одном сечении — по обрезу фундамента. Для узких опор с консольными ригелями требуется проверка связи ригеля с опорой. Расчеты тела опоры ведут, если пролетное строение — разрезное балочное, как правило, при трех сочетаниях нагрузок. Сбор нагрузок для определения суммарных усилий по сочетаниям также рационально выполнять в табличной форме (табл. 3). Как показано в табл. 2, расчетные усилия от каждой нагрузки определяют с теми коэффициентами перегрузки, которые в сочетаниях могут создать невыгодные условия работы конструкции. В табл. 3 лучше привести сразу суммарные усилия из табл. 2 в соответствии с перечисленными ниже сочетаниями: 2. На наибольшее горизонтальное воздействие вдоль моста (рис. 128,6): от собственного веса пролетного строения и опоры Nп’, Nп” и Nо при учете гидростатического давления, от временной вертикальной автомобильной нагрузки и толпы, расположенных на большем пролете l1, по всей ширине проезжей части и на двух тротуарах — Nв’, от торможения — Tт; (может быть вместо торможения — действие сил от навала судов вдоль оси моста); сочетание нагрузок дополнительное, поэтому для временных вертикальных нагрузок и их воздействий коэффициенты перегрузок равны 0,8 n; расчетные постоянные нагрузки принимают в двух вариантах — при nп>1 и при nп=0,9, так как более невыгодное воздействие их может быть установлено только при соответствующей расчетной проверке сечения; суммарные усилия: 3. На наибольшее горизонтальное воздействие поперек моста (рис. 128, в): от собственного веса пролетного строения Nп’; Nп” и опоры Nо при учете гидростатического давления, от временной вертикальной нагрузки на пролетах l1 и l2, придвинутой к низовому бордюру тротуара, толпой загружается один тротуар; число колонн автомобильной нагрузки принимают по указаниям, приведенным ниже; на давление льда при низком ледоходе (первой подвижке) Tнл или при высоком ледоходе Твл, какое из них создает худшие условия работы опоры, (вместо ледовой нагрузки может быть действие сил от навала судов поперек оси моста); на воздействие поперечных ударов в низовую сторону Tп или на поперечную ветровую нагрузку W; сочетание нагрузок дополнительное, при коэффициенте перегрузки 0,8 n и nп≥1 или nп = 0,9; суммарные усилия: Гидростатическое, давление учитывают для речных опор в следующих случаях: Здесь F — площадь расчетного сечения: φ — коэффициент понижения несущей способности при сжатии с продольным изгибом, определяемый по CH 200-62 в зависимости от величин β или λ, β = l0/b и λ = l0/r — для бутобетонных и бетонных опор; β = 0,9l0/b и λ = 0,8l0/r — для опор из любой каменной кладки или из бетонных блоков на растворе; b — наименьший размер сечения; r=√I/F — радиус инерции поперечного сечения; l0 — свободная длина элемента. В отношении продольного изгиба массивные опоры рассматривают как стержни с одним жестко заделанным и другим шарнирно неподвижным концами, тогда l0 = O/H, где H — высота опоры от верха оголовка (ригеля) до обреза фундамента. Внецентренно сжатые элементы рассчитывают на прочность (устойчивость) в зависимости от относительной величины эксцентриситета, малого или большого (рис. 129,б). Здесь φи = φ, если опора из бетона или бутобетона, φи = φ+φс/2, если опора из каменной кладки; φс — коэффициент снижения несущей способности для площади Fc, зависящей от β = h’/ac или λ = h’/rc, где ac и rc — высота и радиус инерции площади Fc, h’ — высота части элемента с однозначной эпюрой изгибающего момента; е = yс — расстояние от точки приложения сил ΣN до менее нагруженной грани сечения. Эта проверка имеет целью не допустить чрезмерное раскрытие трещин, которые могут появиться в растянутой зоне опор, ограничить самую длину этой растянутой зоны и этим предотвратить выветривание и повысить срок службы опоры. Двухъярусные опоры с верхней железобетонной столбчатой частью и нижней массивной или столбчатые до обреза фундамента опоры рассчитывают по месту заделки столбов. Самую заделку не проверяют, если выдержано конструктивное требование о закреплении столбов в массивной части (фундаменте) заделкой их концов в стаканные гнезда на глубину не менее 1,1 наибольшего поперечного сечения столба. Расчеты ведут при тех же трех сочетаниях нагрузок, определяемых, как указывалось выше: первом основном, втором и третьем — дополнительных, при действии горизонтальных нагрузок вдоль и поперек моста. При первом и втором сочетаниях временная нагрузка располагается на пролетах, как указано для расчета массивной опоры, при толпе на одном тротуаре, но в третьем сочетании автомобильная нагрузка принимается в виде двух колонн автомобилей, придвинутых к низовому тротуару. Вертикальные постоянные усилия и горизонтальные нагрузки во всех случаях принимают поровну распределенными между отолбами. Несимметричное расположение временной нагрузки при третьем сочетании вызывает вертикальную перегрузку столба, а не изгибающий момент в теле опоры, как это было для массивной опоры. Указания по учету гидростатического давления и применению коэффициентов перегрузки для постоянной нагрузки те же. Здесь ледовая нагрузка Tл может быть при низком ледоходе — Tнл и при высоком ледоходе — Твлл, какое из этих воздействий создает больший изгибающий момент в расчетном сечении. Для гибких столбов необходимо учитывать увеличение эксцентриситета продольной силы вследствие прогиба элемента в плоскости действия момента |
Добавлено Serxio 27-01-2016, 07:59 Просмотров: 3 396
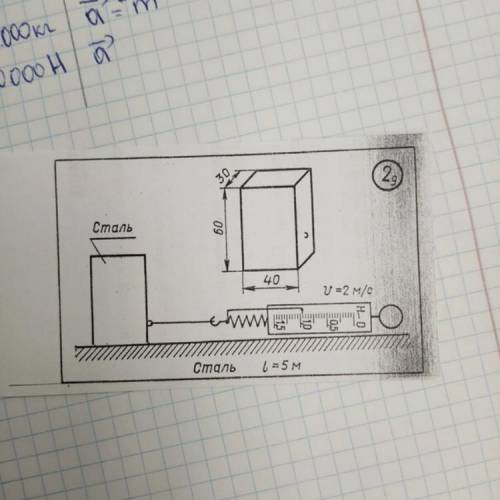
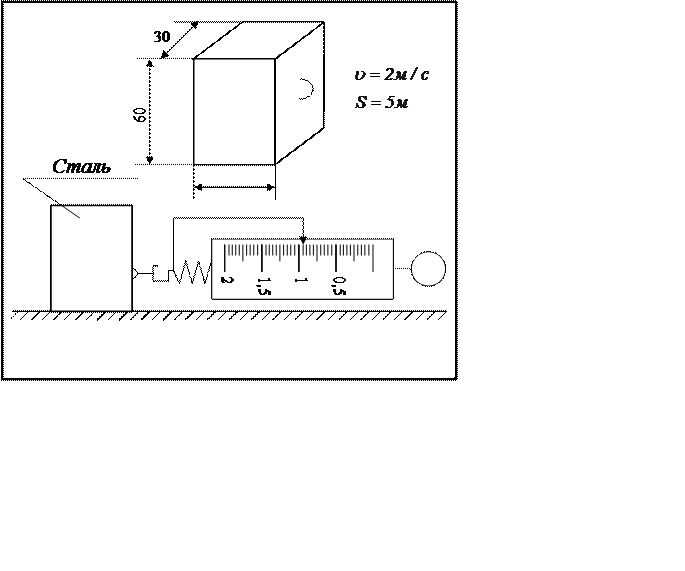
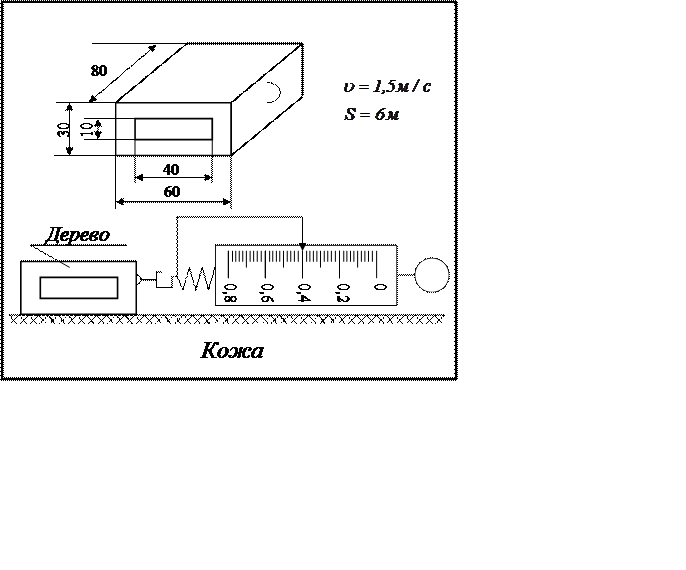
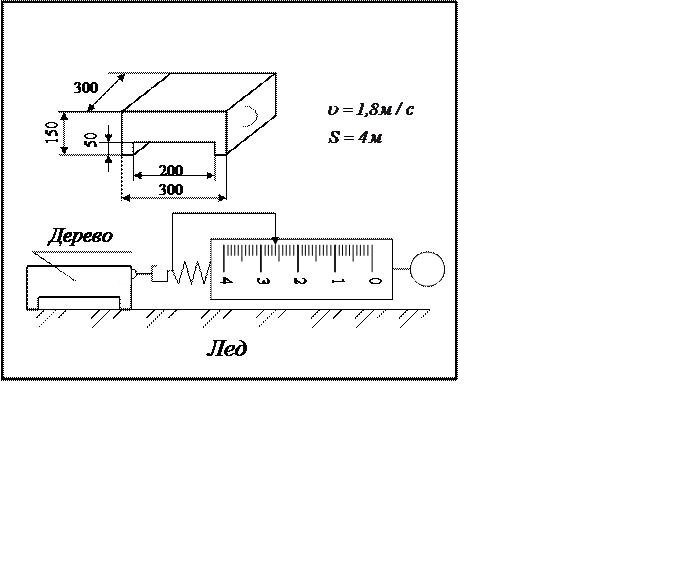
На рисунке изображено тело, которое прикреплено к
динамометру. Размеры тела указаны в миллиметрах. Ниже изображен динамометр,
который двигают по поверхности, с указанной в карточке скоростью. Используя все
данные, выполните задания, ответьте на вопросы.
1
Вычислите площадь опоры тела.
2
Вычислите объем тела и его массу.
3
С какой силой тело давит на опору?
4
Каково давление тела на
поверхность?
5
Определите цену деления шкалы
динамометра.
6
Чему равна сила трения, если
движение равномерное со скоростью ?
7
Вычислите коэффициент трения.
8
Чему будет равна сила трения покоя
при уменьшении величины тяги в 2 раза?
9
Вычислите механическую работу силы
тяги на пути S.
10
Чему равен импульс тела?
11
Вычислите мощность при движении
тела.
12
Вычислите кинетическую энергию
тела.
 |
Вариант 1
Вариант 2
 |
Вариант 3
 |
 |
Вариант 4
Вариант 5
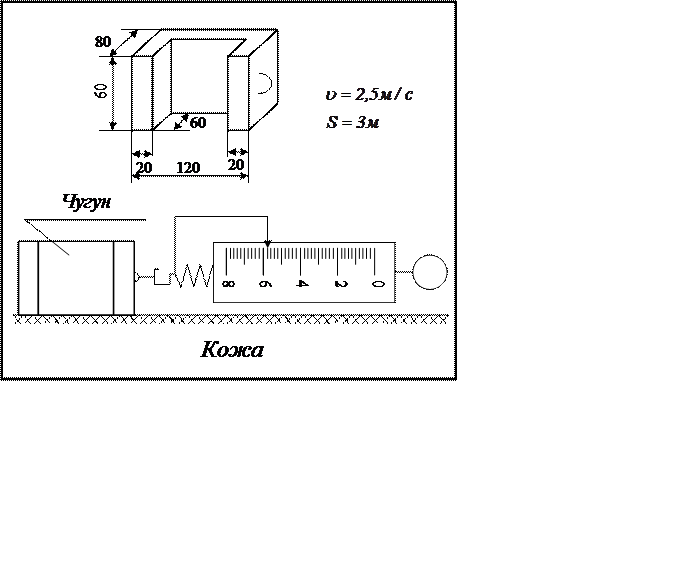 |
Вариант 6
 |
Вариант 7
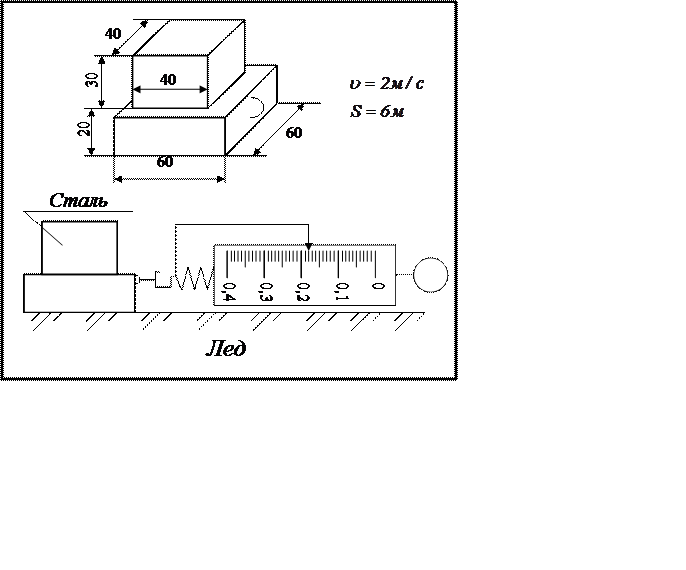 |
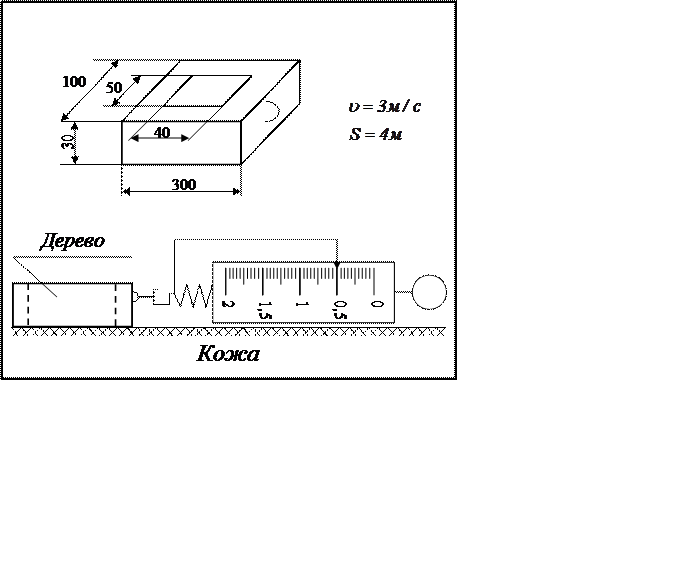 |
Вариант 8
Вариант 9
 |
Вариант 10
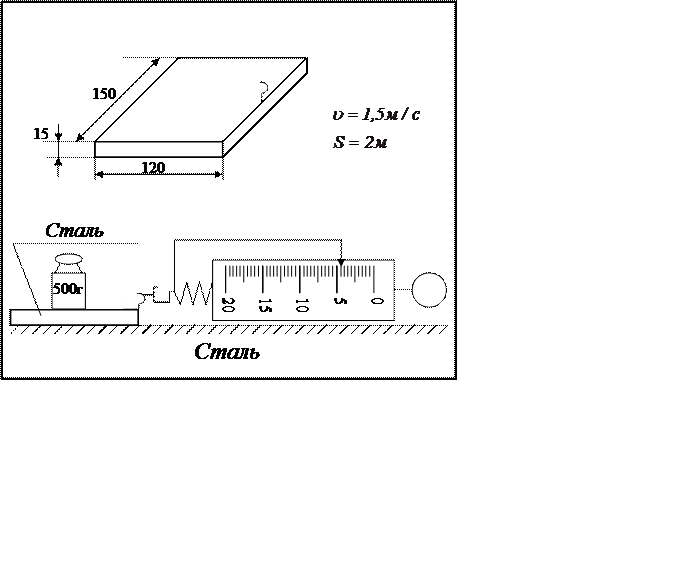 |
Вариант 11
 |
Сила трения, работа и мощность, импульс тела
Образец решения
Вариант 4
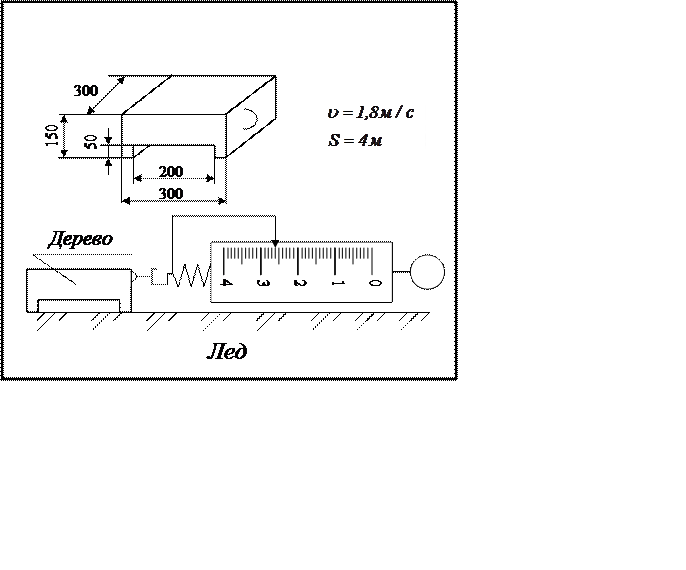 |
1 Площадь опоры тела:
2 Объем тела:
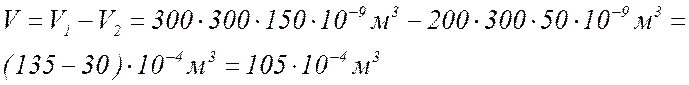
Масса тела: , дерево
,
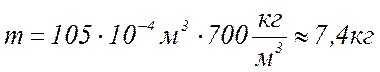
3 Сила давления:
4 Давление: 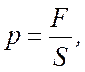
5 Цена деления шкалы: .
6 Сила трения: .
7 Коэффициент трения: 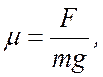
8 Сила трения покоя:
9 Импульс тела: ,
.
10 Механическая работа: ,
,
11 Мощность: ,
,
12 Кинетическая энергия: 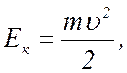
График изотермы и адиабаты газа
На графике даны изотерма и адиабата газа в координатах
(P, V). Используя данные графики, ответьте на вопросы, выполните задания.
1 Какому объему и какому давлению
соответствует сторона клетки?
2 По изотерме найдите произведение
давление газа на его объем.
3 Вычислите температуру газа в
состояниях, отмеченных на адиабате
точками B, C, D, если в состоянии A температура
газа 27°C.
4 Какова разница в температуре газа
между состояниями M и D?
5 Вычислите массу газа, если его
молекулярная масса равна 32 г/моль.
Универсальную газовую постоянную для упрощения
расчетов
принять равной:
Вариант 1
 |
Вариант 2
 |
Вариант 3
 |
Вариант 4
 |
Вариант 5
 |
Вариант 6
 |
Вариант 7
Вариант 8
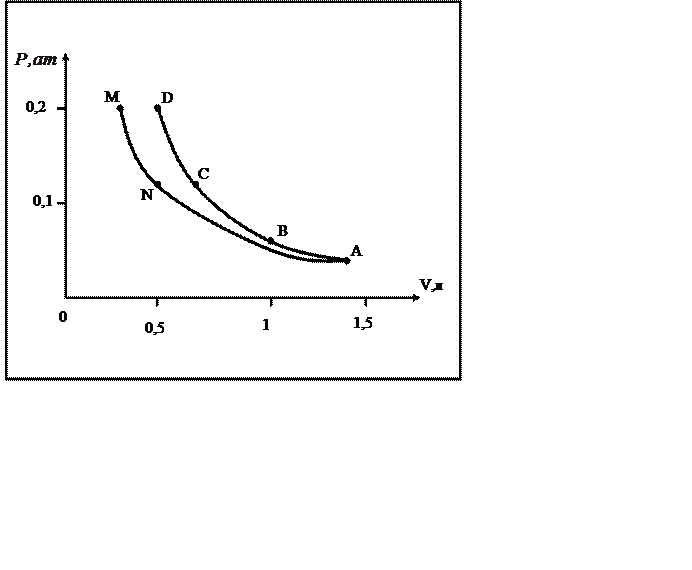 |
Вариант 9
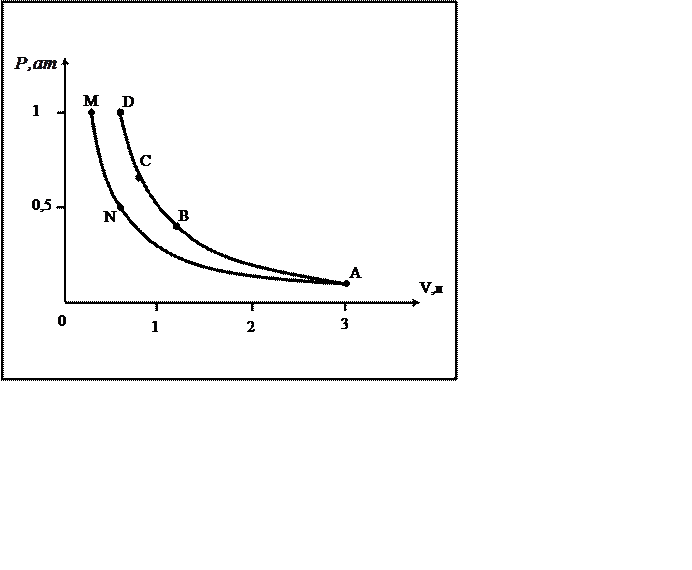 |
Вариант 10
 |
Вариант 11
 |
Вариант 12
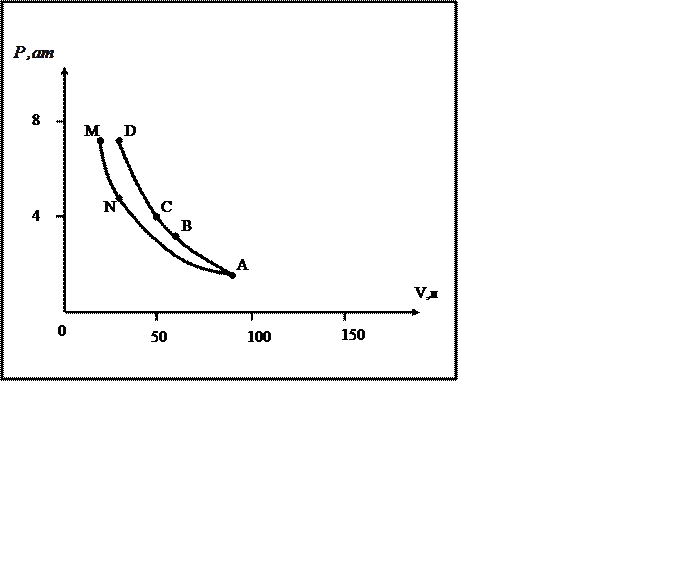 |
График изотермы и адиабаты газа
Образец решения
Вариант 8
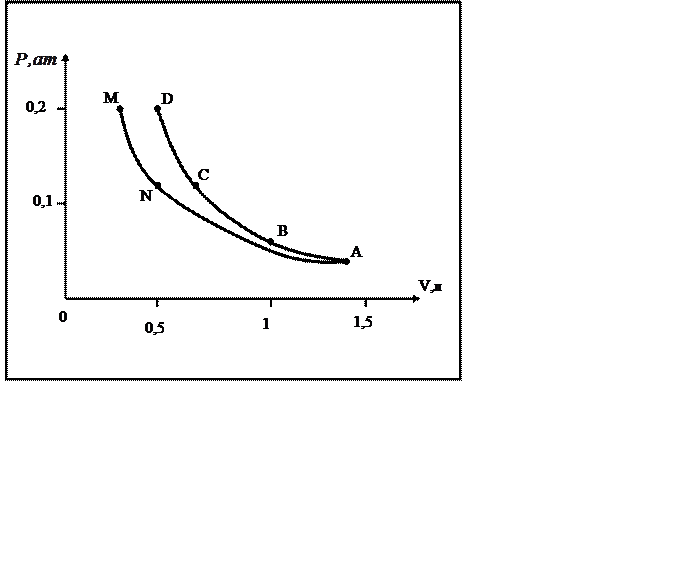 |
1
Сторона клетки соответствует
объему: , давлению
2
Изотермой на графике является
кривая ANM, так как произведение давление газа на объем во всех
состояниях, отмеченных точками на этой кривой, остается неизменным и равным: (в точке А),
(в
точке N), (в точке М),
.
3
По уравнению Менделеева-Клапейрона
вычисляют температуру данной массы газа в состояниях В, С, D,
если в состоянии А температура газа :
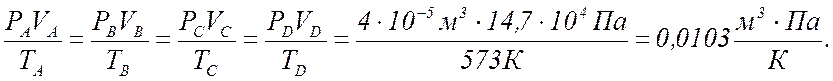
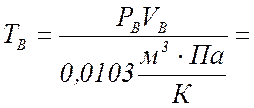
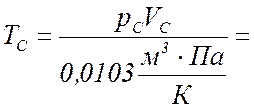
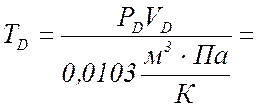
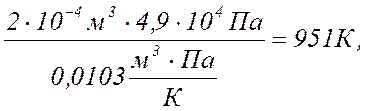
4 Разница в температуре между состояниями M и D
газа равна:
5 Масса газа вычисляется по уравнению Менделеева –
Клапейрона: 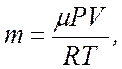
Графики изменения состояния идеального газа
в координатах V,
T или Р,V
На графике изображено изменение состояния газа в
координатах V,T. Ответьте на вопросы, выполните задания, используя
данные графика.