Определение объемов геометрических тел является одной из важных задач пространственной геометрии. В данной статье рассматривается вопрос, что такое призма с шестиугольным основанием, а также приводится формула объема правильной шестиугольной призмы.
Определение призмы
С точки зрения геометрии призмой называется фигура в пространстве, которая образована двумя одинаковыми многоугольниками, расположенными в параллельных плоскостях. А также несколькими параллелограммами, которые эти многоугольники соединяют в единую фигуру.
В трехмерном пространстве призму произвольной формы можно получить, если взять любой многоугольник и отрезок. Причем последний плоскости многоугольника принадлежать не будет. Тогда, располагая этот отрезок от каждой вершины многоугольника, можно получить параллельный перенос последнего в другую плоскость. Образованная таким способом фигура будет призмой.
Чтобы иметь наглядное представление о рассматриваемом классе фигур, приведем рисунок четырехугольной призмы.
Многие знают эту фигуру под названием параллелепипеда. Видно, что два одинаковых многоугольника призмы представляют собой квадраты. Их называют основаниями фигуры. Остальные четыре ее стороны – прямоугольники, то есть это частный случай параллелограммов.
Шестиугольная призма: определение и виды
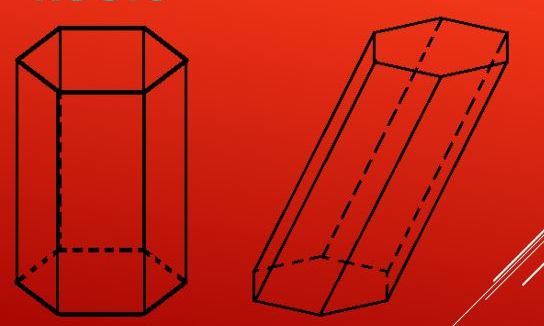
Прежде чем приводить формулу, как определяется объем шестиугольной правильной призмы, необходимо четко понять, о какой фигуре пойдет речь. Шестиугольная призма имеет в основаниях шестиугольник. То есть, плоский многоугольник с шестью сторонами, углов столько же. Боковые стороны фигуры так же, как и для любой призмы, в общем случае являются параллелограммами. Сразу отметим, что шестиугольное основание может быть представлено как правильным, так и неправильным шестиугольником.
Расстояние между основаниями фигуры – это ее высота. Далее мы будем обозначать ее буквой h. Геометрически высота h представляет собой отрезок, перпендикулярный обоим основаниям. Если этот перпендикуляр:
- опущен с геометрического центра одного из оснований;
- пересекает второе основание также в геометрическом центре.
Фигура в этом случае называется прямой. В любом другом случае призма будет косоугольной или наклонной. Разницу между этими видами шестиугольной призмы можно увидеть с первого взгляда.
Прямая шестиугольная призма – это фигура, имеющая в основании правильные шестиугольники. При этом она является прямой. Рассмотрим подробнее ее свойства.
Элементы правильной шестиугольной призмы
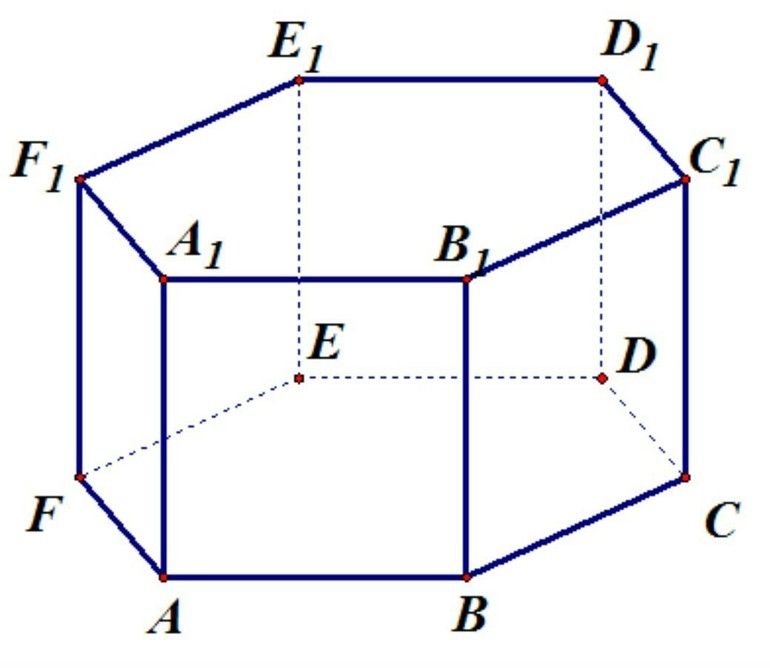
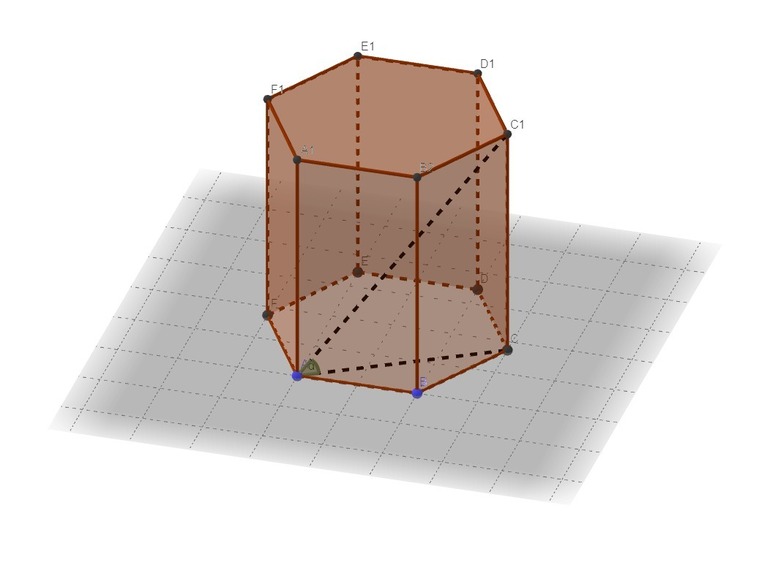
Чтобы понять, как вычислить объем правильной шестиугольной призмы (формула приведена ниже в статье), необходимо также разобраться, из каких элементов состоит фигура, а также какими свойствами она обладает. Чтобы было легче анализировать фигуру, покажем ее на рисунке.
Главными ее элементами являются грани, ребра и вершины. Количества этих элементов подчиняется теореме Эйлера. Если обозначить Р – число ребер, В – количество вершин и Г – граней, тогда можно записать равенство:
Р = Г + В – 2.
Проверим его. Число граней рассматриваемой фигуры равно 8. Две из них – это правильные шестиугольники. Шесть граней представляет собой прямоугольники, это видно из рисунка. Число вершин составляет 12. Действительно, 6 вершин принадлежат одному основанию, и 6 другому. Согласно формуле, число ребер должно равняться 18, что является справедливым. 12 ребер лежат в основаниях и 6 образуют параллельные друг другу стороны прямоугольников.
Переходя к получению формулы объема правильной шестиугольной призмы, следует остановить свое внимание на одном важном свойстве этой фигуры: прямоугольники, образующие боковую поверхность, равны между собой и перпендикулярны обоим основаниям. Это приводит к двум важным следствиям:
- Высота фигуры равна длине ее бокового ребра.
- Любое сечение боковой поверхности пирамиды, выполненное с помощью секущей плоскости, которая параллельна основаниям, является правильным шестиугольником, равным этим основаниям.
Площадь шестиугольника
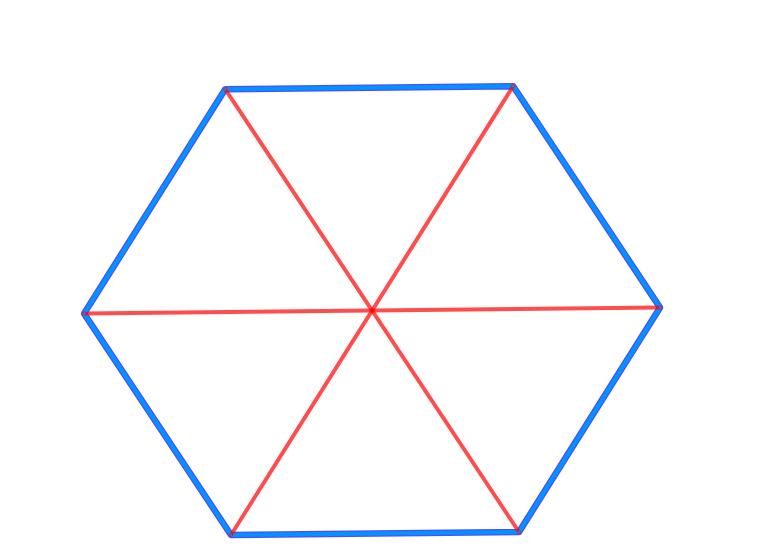
Можно интуитивно догадаться, что эта площадь основания фигуры появится в формуле объема правильной призмы шестиугольной. Поэтому в данном пункте статьи найдем эту площадь. Правильный шестиугольник, разделенный на 6 одинаковых треугольников, вершины которых пересекаются в его геометрическом центре, показан ниже:
Каждый из этих треугольников является равносторонним. Доказать это не очень сложно. Поскольку вся окружность имеет 360o, то углы треугольников вблизи геометрического центра шестиугольника равны 360o/6=60o. Расстояния от геометрического центра до вершин шестиугольника являются одинаковыми.
Последнее означает, что все 6 треугольников будут равнобедренными. Поскольку один из углов равнобедренных треугольников равен 60o, значит, два остальных угла тоже равны по 60o. ((180o-60o)/2) – треугольники равносторонние.
Обозначим длину стороны шестиугольника буквой a. Тогда площадь одного треугольника будет равна:
S1 = 1/2*√3/2*a*a = √3/4*a2.
Формула получена на основании стандартного выражения для площади треугольника. Тогда площадь S6 для шестиугольника будет:
S6 = 6*S1 = 6*√3/4*a2 = 3*√3/2*a2.
Формула определения объема правильной шестиугольной призмы
Чтобы записать формулу для объема рассматриваемой фигуры, следует учесть приведенную выше информацию. Для произвольной призмы объем пространства, ограниченный ее гранями, вычисляется так:
V = h*So.
То есть, V равен произведению площади основания So на высоту h. Поскольку мы знаем, что высота h равна длине бокового ребра b для шестиугольной правильной призмы, а площадь ее основания соответствует S6, то формула объема правильной шестиугольной призмы примет вид:
V6 = 3*√3/2*a2*b.
Пример решения геометрической задачи
Дана шестиугольная правильная призма. Известно, что она вписана в цилиндр радиусом 10 см. Высота призмы в два раза больше стороны ее основания. Необходимо найти объем фигуры.
Чтобы найти требуемую величину, необходимо знать длину стороны и бокового ребра. При рассмотрении правильного шестиугольника было показано, что его геометрический центр расположен в середине описанной вокруг него окружности. Радиус последней равен расстоянию от центра до любой из вершин. То есть он равен длине стороны шестиугольника. Эти рассуждения приводят к следующим результатам:
a = r = 10 см;
b = h = 2*a = 20 см.
Подставляя эти данные в формулу объема правильной шестиугольной призмы, получим ответ: V6≈5196 см3 или около 5,2 литра.

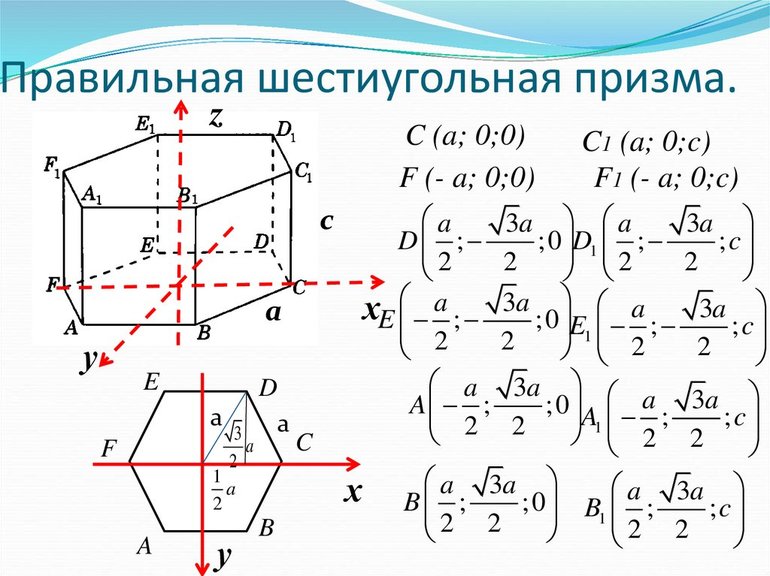
Обозначения
- $ABCDEFA_1B_1C_1D_1E_1F_1$ — правильная шестиугольная призма
- $a$ — длина стороны основания призмы
- $h$ — длина бокового ребра призмы
- $S_{text{осн.}}$ — площадь основания призмы
- $S_{text{бок.}}$ — площадь боковой грани призмы
- $S_{text{полн.}}$ — площадь полной поверхности призмы
- $V_{text{призмы}}$ — объем призмы
Площадь оснований призмы
В основаниях призмы находятся правильные шестиугольники со стороной $a$. По свойствам правильного шестиугольника, площадь оснований призмы равна $$ S_{text{осн.}}=frac{3sqrt{3}}{2}cdot a^2 $$ Таким образом, получается, что $S_{ABCDEF}=S_{A_1B_1C_1D_1E_1F_1}=frac{3sqrt{3}}{2}cdot a^2$.
Площадь полной поверхности призмы
Площадь полной поверхности призмы складывается из площадей боковых граней призмы и площадей ее оснований. Каждая из боковых граней призмы является прямоугольником со сторонами $a$ и $h$. Следовательно, по свойствам прямоугольника $$ S_{text{бок.}}=acdot h $$ У призмы шесть боковых граней и два основания, следовательно, площадь ее полной поверхности равна $$ S_{text{полн.}}=6cdot S_{text{бок.}}+2cdot S_{text{осн.}}=6cdot acdot h+2cdot frac{3sqrt{3}}{2}cdot a^2$$
Объем призмы
Объем призмы вычисляется как произведение площади ее основания на ее высоту. Высотой правильной призмы является любое из ее боковых ребер, например, ребро $AA_1$. В основании правильной шестиугольной призмы находится правильный шестиугольник, площадь которого нам известна. Получаем $$ V_{text{призмы}}=S_{text{осн.}}cdot AA_1=frac{3sqrt{3}}{2}cdot a^2cdot h $$
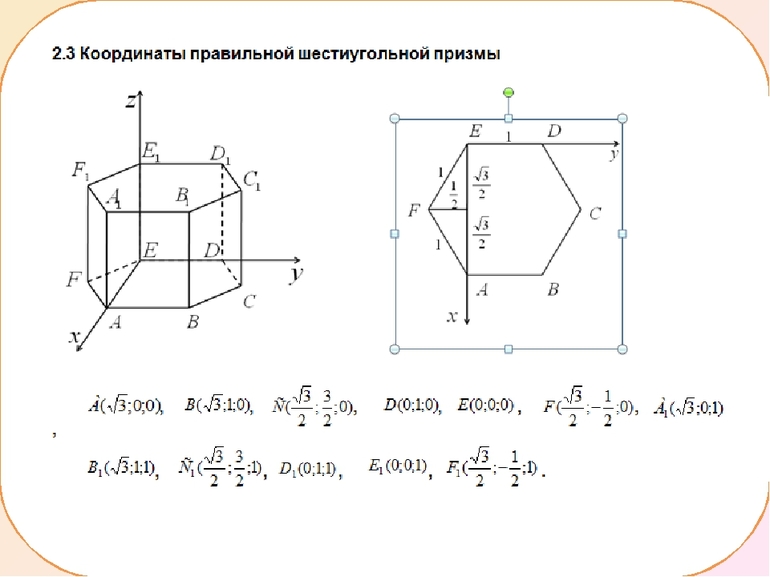
Правильный шестиугольник в основаниях призмы

Находим $EA_1$

- $AA_1=h$
- $AE=sqrt{3}cdot a$ — как мы только что выяснили
- $angle EAA_1=90^{circ}$ — по свойствам правильной призмы
Таким образом, получается, что треугольник $AEA_1$ прямоугольный. По свойствам прямоугольного треугольника $$ EA_1=sqrt{AA_1^2+AE^2}=sqrt{h^2+3cdot a^2} $$ Если $h=a$, то тогда $$ EA_1=2cdot a $$ После аналогичных рассуждений получаем, что $FB_1=AC_1=BD_1=CE_1=DF_1=sqrt{h^2+3cdot a^2}$.
Находим $EB_1$

- $BB_1=h$
- $BE=2cdot a$ — потому что $EO=OB=a$
- $angle EBB_1=90^{circ}$ — по свойствам правильной призмы
Таким образом, получается, что треугольник $BEB_1$ прямоугольный. По свойствам прямоугольного треугольника $$ EB_1=sqrt{BB_1^2+BE^2}=sqrt{h^2+4cdot a^2} $$ Если $h=a$, то тогда $$ EB_1=sqrt{5}cdot a $$ После аналогичных рассуждений получаем, что $FC_1=AD_1=BE_1=CF_1=DA_1=sqrt{h^2+4cdot a^2}$.
Находим $OF_1$

- $FF_1=h$
- $FO=a$
- $angle OFF_1=90^{circ}$ — по свойствам правильной призмы
Таким образом, получается, что треугольник $FOF_1$ прямоугольный. По свойствам прямоугольного треугольника $$ OF_1=sqrt{FF_1^2+OF^2}=sqrt{h^2+a^2} $$ Если $h=a$, то тогда $$ OF_1=sqrt{2}cdot a $$ После аналогичных рассуждений получаем, что $OA_1=OB_1=OC_1=OD_1=OE_1=sqrt{h^2+a^2}$.
Находим $FE_1$

- $EE_1=h$
- $FE=a$
- $angle FEE_1=90^{circ}$ — по свойствам правильной призмы
Таким образом, получается, что треугольник $FEE_1$ прямоугольный. По свойствам прямоугольного треугольника $$ FE_1=sqrt{FE^2+EE_1^2}=sqrt{h^2+a^2} $$ Если $h=a$, то тогда $$ FE_1=sqrt{2}cdot a $$ После аналогичных рассуждений получаем, что длины диагоналей остальных боковых граней призмы также равны $sqrt{h^2+a^2}$.
Определение призмы
С точки зрения геометрии призмой называется фигура в пространстве, которая образована двумя одинаковыми многоугольниками, расположенными в параллельных плоскостях. А также несколькими параллелограммами, которые эти многоугольники соединяют в единую фигуру.
В трехмерном пространстве призму произвольной формы можно получить, если взять любой многоугольник и отрезок. Причем последний плоскости многоугольника принадлежать не будет. Тогда, располагая этот отрезок от каждой вершины многоугольника, можно получить параллельный перенос последнего в другую плоскость. Образованная таким способом фигура будет призмой.
Чтобы иметь наглядное представление о рассматриваемом классе фигур, приведем рисунок четырехугольной призмы.
Многие знают эту фигуру под названием параллелепипеда. Видно, что два одинаковых многоугольника призмы представляют собой квадраты. Их называют основаниями фигуры. Остальные четыре ее стороны — прямоугольники, то есть это частный случай параллелограммов.
Примеры из реальной жизни
Гигантский гексагон
Гигантский гексагон — уникальное атмосферное явление на Сатуре, которое выглядит как грандиозный вихрь в форме правильного шестиугольника. Известно, что сторона гигантского гексагона составляет 13 800 км, благодаря чему мы можем определить площадь «облака». Для этого достаточно ввести значение стороны в форму калькулятора и получить результат:
S = 494 777 633
Таким образом, площадь атмосферного вихря на Сатурне приблизительно составляет 494 777 633 квадратных километров. Поистине впечатляет.
Гексагональные шахматы
Мы все привыкли к шахматному полю, разделенному на 64 квадратные ячейки. Однако существуют и гексагональные шахматы, игровое поле которых разделено на 91 правильный шестиугольник. Давайте определим площадь игровой доски для гексагональной версии известной игры. Пусть сторона ячейки составляет 2 сантиметра. Площадь одной игровой клетки составит:
S = 10,39
Тогда площадь всей доски будет равна 91 × 10,39 = 945,49 квадратных сантиметров.
Шестиугольная призма: определение и виды
Прежде чем приводить формулу, как определяется объем шестиугольной правильной призмы, необходимо четко понять, о какой фигуре пойдет речь. Шестиугольная призма имеет в основаниях шестиугольник. То есть, плоский многоугольник с шестью сторонами, углов столько же. Боковые стороны фигуры так же, как и для любой призмы, в общем случае являются параллелограммами. Сразу отметим, что шестиугольное основание может быть представлено как правильным, так и неправильным шестиугольником.
Расстояние между основаниями фигуры — это ее высота. Далее мы будем обозначать ее буквой h. Геометрически высота h представляет собой отрезок, перпендикулярный обоим основаниям. Если этот перпендикуляр:
- опущен с геометрического центра одного из оснований;
- пересекает второе основание также в геометрическом центре.
Фигура в этом случае называется прямой. В любом другом случае призма будет косоугольной или наклонной. Разницу между этими видами шестиугольной призмы можно увидеть с первого взгляда.
Прямая шестиугольная призма — это фигура, имеющая в основании правильные шестиугольники. При этом она является прямой. Рассмотрим подробнее ее свойства.
Немного фактов из истории
Геометрия использовалась еще в древнем Вавилоне и прочих государствах, существовавших в одно время с ним. Вычисления помогали при возведении значительных сооружений, так как благодаря ей зодчие знали как выдержать вертикаль, правильно составить план, определить высоту.
Эстетика тоже имела большое значение, и здесь снова шла в ход геометрия. Сегодня этой науки нужны строителю, закройщику, архитектору, да и не специалисту тоже.
Поэтому лучше уметь рассчитывать S фигур, понимать, что формулы могут пригодиться на практике.
Элементы правильной шестиугольной призмы
Чтобы понять, как вычислить объем правильной шестиугольной призмы (формула приведена ниже в статье), необходимо также разобраться, из каких элементов состоит фигура, а также какими свойствами она обладает. Чтобы было легче анализировать фигуру, покажем ее на рисунке.
Главными ее элементами являются грани, ребра и вершины. Количества этих элементов подчиняется теореме Эйлера. Если обозначить Р — число ребер, В — количество вершин и Г — граней, тогда можно записать равенство:
Р = Г + В — 2.
Проверим его. Число граней рассматриваемой фигуры равно 8. Две из них — это правильные шестиугольники. Шесть граней представляет собой прямоугольники, это видно из рисунка. Число вершин составляет 12. Действительно, 6 вершин принадлежат одному основанию, и 6 другому. Согласно формуле, число ребер должно равняться 18, что является справедливым. 12 ребер лежат в основаниях и 6 образуют параллельные друг другу стороны прямоугольников.
Переходя к получению формулы объема правильной шестиугольной призмы, следует остановить свое внимание на одном важном свойстве этой фигуры: прямоугольники, образующие боковую поверхность, равны между собой и перпендикулярны обоим основаниям. Это приводит к двум важным следствиям:
- Высота фигуры равна длине ее бокового ребра.
- Любое сечение боковой поверхности пирамиды, выполненное с помощью секущей плоскости, которая параллельна основаниям, является правильным шестиугольником, равным этим основаниям.
Шестиугольник в реальности
Гексагоны часто встречаются в реальной жизни. К примеру, сечения гаек или карандашей имеют шестиугольную форму, благодаря чему обеспечивается удобный обхват предмета. Шестиугольник — это эффективная геометрическая фигура, способная замостить плоскость без пробелов и наложений. Именно поэтому шестиугольную форму часто имеют декоративные отделочные материалы, например, кафельная и тротуарная плитка или гипсокартонные панели.
Эффективность гексагона делает его популярным и в природе. Пчелиные соты обладают именно шестиугольной формой, благодаря которой пространство улья заполняется без пробелов. Еще одним примером гексагонального замощения плоскости является Тропа Великанов — памятник живой природы, сформированный во время извержения вулкана. Вулканический пепел был спрессован в шестиугольные колонны, которые замостили поверхность побережья Северной Ирландии.
Площадь шестиугольника
Можно интуитивно догадаться, что эта площадь основания фигуры появится в формуле объема правильной призмы шестиугольной. Поэтому в данном пункте статьи найдем эту площадь. Правильный шестиугольник, разделенный на 6 одинаковых треугольников, вершины которых пересекаются в его геометрическом центре, показан ниже:
Каждый из этих треугольников является равносторонним. Доказать это не очень сложно. Поскольку вся окружность имеет 360o, то углы треугольников вблизи геометрического центра шестиугольника равны 360o/6=60o. Расстояния от геометрического центра до вершин шестиугольника являются одинаковыми.
Последнее означает, что все 6 треугольников будут равнобедренными. Поскольку один из углов равнобедренных треугольников равен 60o, значит, два остальных угла тоже равны по 60o. ((180o-60o)/2) — треугольники равносторонние.
Обозначим длину стороны шестиугольника буквой a. Тогда площадь одного треугольника будет равна:
S1 = 1/2*√3/2*a*a = √3/4*a2.
Формула получена на основании стандартного выражения для площади треугольника. Тогда площадь S6 для шестиугольника будет:
S6 = 6*S1 = 6*√3/4*a2 = 3*√3/2*a2.
Выпуклый шестиугольник
Гескагон — это правильный выпуклый многоугольник, соответственно, все его углы равны, все стороны равны, а если провести отрезок через две соседние вершины, то вся фигура окажется по одну сторону от этого отрезка. Как и в любой правильный n-угольник, вокруг гексагона можно описать окружность или вписать ее вовнутрь. Главная особенность шестиугольника заключается в том, что длина радиуса описанной окружности совпадает с длиной стороны многоугольника. Благодаря этому свойству можно легко найти площадь гексагона по формуле:
S = 2,59 R2 = 2,59 a2.
Кроме того, радиус вписанной окружности соотносится со стороной фигуры как:
r = 3,46 a.
Из этого следует, что вычислить площадь шестиугольника можно, оперируя одной из трех переменных на выбор.
Гексаграмма
Звездчатый правильный шестиугольник предстает перед нами в виде шестиконечной звезды. Такая фигура образуется путем наложения друг на друга двух равносторонних треугольников. Самой известной реальной гексаграммой является Звезда Давида — символ еврейского народа.
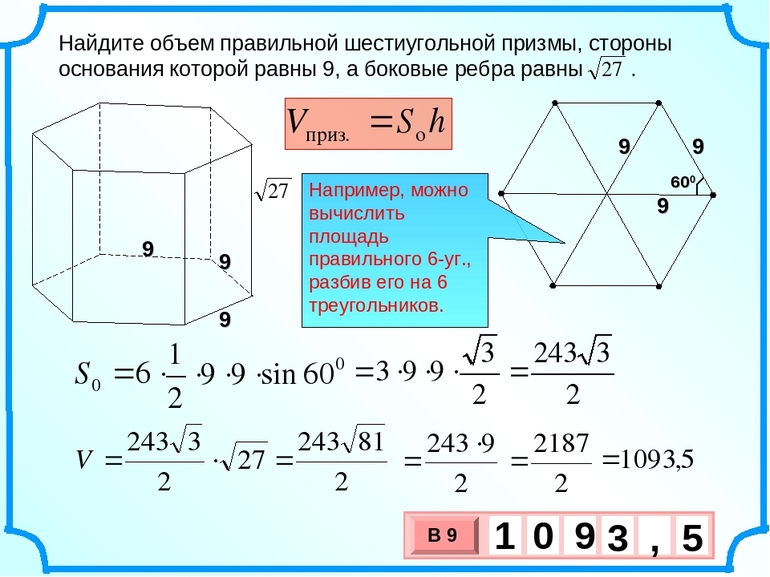
Формула определения объема правильной шестиугольной призмы
Чтобы записать формулу для объема рассматриваемой фигуры, следует учесть приведенную выше информацию. Для произвольной призмы объем пространства, ограниченный ее гранями, вычисляется так:
V = h*So.
То есть, V равен произведению площади основания So на высоту h. Поскольку мы знаем, что высота h равна длине бокового ребра b для шестиугольной правильной призмы, а площадь ее основания соответствует S6, то формула объема правильной шестиугольной призмы примет вид:
V6 = 3*√3/2*a2*b.
Как находить площадь неправильного шестиугольника
Есть несколько вариантов:
- Разбивка 6-угольника на другие фигуры.
- Метод трапеции.
- Расчет S неправильных многоугольников с помощью осей координат.
Выбор способа диктуется исходными данными.
Метод трапеции
Шестиугольник делится на отдельные трапеции, после чего вычисляется площадь каждой полученной фигуры.
Использование осей координат
Используем координаты вершин многоугольника:
- В таблицу записываем координаты вершин x и y . Последовательно выбираем вершины, «двигаясь» против часовой стрелки, завершая список повторной записью координат первой вершины.
- Умножаем значения координаты x 1-й вершины на значение y 2-й вершины, и продолжаем так умножать. Складываем полученные результаты.
- Значения координат y1-й вершины умножаем на значения координат x 2-й вершины. Складываем результаты.
- Вычитаем сумму, полученную на 4-м этапе из суммы, полученной на третьем этапе.
- Делим результат, полученный на предыдущем этапе, и находим, что искали.
Scisne?
Правильный шестиугольник (гексагон) — это правильный многоугольник с шестью сторонами.
Математические свойства
Особенность правильного шестиугольника — равенство его стороны и радиуса описанной окружности , поскольку
.
Все углы равны 120°.
Радиус вписанной окружности равен:
.
Периметр правильного шестиугольника равен: Площадь правильного шестиугольника рассчитывается по формулам:
, .
Шестиугольники замощают плоскость, то есть могут заполнять плоскость без пробелов и наложений, образуя так называемый паркет.
Шестиугольный паркет (шестиугольный паркетаж) — замощение плоскости равными правильными шестиугольниками, расположенными сторона к стороне.
Шахматная раскраска шестиугольного паркета
Шестиугольный паркет является двойственным треугольному паркету: если соединить центры смежных шестиугольников, то проведённые отрезки дадут треугольный паркетаж. Символ Шлефли шестиугольного паркета — {6,3}, что означает, что в каждой вершине паркета сходятся три шестиугольника.
Шестиугольный паркет является наиболее плотной упаковкой кругов на плоскости. В двумерном евклидовом пространстве наилучшим заполнением является размещение центров кругов в вершинах паркета, образованного правильными шестиугольниками, в котором каждый круг окружен шестью другими. Плотность данной упаковки равна . В 1940 году было доказано, что данная упаковка является самой плотной.
Наиболее плотная упаковка кругов на плоскости
Правильный шестиугольник со стороной является универсальной покрышкой, то есть всякое множество диаметра можно покрыть правильным шестиугольником со стороной (лемма Пала).
Правильный шестиугольник можно построить с помощью циркуля и линейки. Ниже приведён метод построения, предложенный Евклидом в «Началах», книга IV, теорема 15.
Построение правильного шестиугольника с помощью циркуля и линейки
Правильный шестиугольник в природе, технике и культуре
Пчелиные соты показывают разбиение плоскости на правильные шестиугольники. Шестиугольная форма больше остальных позволяет сэкономить на стенках, то есть на соты с такими ячейками уйдёт меньше воска.
Пчелиные соты
Некоторые сложные кристаллы и молекулы, например графит, имеют гексагональную кристаллическую решётку.
Кристаллическая решетка графита
Снежинки образуется, когда микроскопические капли воды в облаках притягиваются к пылевым частицам и замерзают. Появляющиеся при этом кристаллы льда, не превышающие поначалу 0,1 мм в диаметре, падают вниз и растут в результате конденсации на них влаги из воздуха. При этом образуются шестиконечные кристаллические формы. Из-за структуры молекул воды между лучами кристалла возможны углы лишь в 60° и 120°. Основной кристалл воды имеет в плоскости форму правильного шестиугольника. На вершинах такого шестиугольника затем осаждаются новые кристаллы, на них — новые, и так получаются разнообразные формы звёздочек-снежинок.
Снежинки
Гигантский гексагон — атмосферное явление на Сатурне.
Гигантский гексагон — устойчивое атмосферное образование на северном полюсе Сатурна, открытое аппаратом Вояджер-1 и наблюдаемое снова в 2006 году аппаратом Кассини-Гюйгенс.
Учёные из Оксфордского университета смогли в лабораторных условиях смоделировать возникновение подобного гексагона. Чтобы выяснить, как возникает такое образование, исследователи поставили на вертящийся стол 30-литровый баллон с водой. Она моделировала атмосферу Сатурна и её обычное вращение. Внутри учёные поместили маленькие кольца, вращающиеся быстрее ёмкости. Это генерировало миниатюрные вихри и струи, которые экспериментаторы визуализировали при помощи зелёной краски. Чем быстрее вращалось кольцо, тем больше становились вихри, заставляя близлежащий поток отклоняться от круговой формы. Таким образом авторам опыта удалось получить различные фигуры — овалы, треугольники, квадраты и, конечно, искомый шестиугольник.
Вращение гексагона на северном полюсе Сатурна
Дорога гигантов — памятник природы из примерно 40 000 соединённых между собой базальтовых (реже андезитовых) колонн, образовавшихся в результате древнего извержения вулкана. Расположен на северо-востоке Северной Ирландии в 3 км к северу от города Бушмилса.
Верхушки колонн образуют подобие трамплина, который начинается у подножья скалы и исчезает под поверхностью моря. Большинство колонн шестиугольные, хотя у некоторых четыре, пять, семь и восемь углов. Самая высокая колонна высотой около 12 м.
Около 50-60 миллионов лет назад, во время палеогенового периода, месторасположение Антрим подвергалось интенсивной вулканической активности, когда расплавленный базальт проникал через отложения, формируя обширные лавовые плато. По мере быстрого охлаждения происходило сокращение объёма вещества (подобное наблюдается при высыхании грязи). Горизонтальное сжатие приводило к характерной структуре шестигранных столбов.
Дорога гигантов
Игровое поле зачастую составляют шестиугольники. Замощение плоскости правильными шестиугольниками является основой для гекса, гексагональных шахмат и других игр на клетчатом поле, полигексов, вариантов модели «Жизнь» и других двумерных клеточных автоматов, кольцевых флексагонов и т.п.
Гексагональные шахматы Глинского. Начальное положение фигур.
Сечение гайки имеет вид правильного шестиугольника.
Гайки
Звезда Давида (гексаграмма) — шестиконечная звезда, образованная двумя правильными треугольниками, символ иудаизма.
При необходимости вычислить объем правильной шестиугольной призмы достаточно знать сторону ее грани
(ребро) a и высоту h. Формула вычисления объема следующая (объем любой призмы равен площади ее
основания, умноженной на высоту, в данном случае берется площадь основания правильного
шестиугольника):
V = (3 * a² / 2) * h * √3
где a — сторона его граней (ребро), h — высота.
Цифр после
запятой:
Результат в:
Пример. Вычислим объем шестигранного простого карандаша типа 7 длиной 177 мм (это
высота призмы h) со стороной грани a = 4,5 мм. V = (3 * 4,5² / 2) * 177 * √3 =9312 (мм³) = 9,312 см³.
Призма – это многогранник, две грани которого являются равными многоугольниками, лежащими в
параллельных плоскостях (эти грани называются основаниями), а остальные грани (называемые боковыми
гранями) являются параллелограммами, у которых стороны общие со сторонами многоугольников. Если у
призмы боковые ребра перпендикулярны плоскости основания, она называется прямой призмой. Все боковые
ребра призмы параллельны и равны по длине. Длина бокового ребра прямой призмы – это ее высота. Если
при этом у прямой призмы основания представляют собой правильные многоугольники, призма называется
правильной. У правильной призмы боковые грани представляют собой равные прямоугольники.
У правильной шестиугольной призмы (другое название – правильная шестигранная призма) основания –
правильные шестиугольники. Примерами правильной шестиугольной призмы являются новый незаточенный
шестигранный карандаш, шестигранная головка болта, башни некоторых средневековых замков, смотревшие
в поле 3 или 4 сторонами.
Общие сведения
Призма представляет собой многогранную объёмную фигуру. Две стороны её всегда конгруэнтные (равные) и расположены относительно друг друга в параллельных плоскостях. Остальные же грани являются параллелограммами и формируют общие боковые основания с параллельными поверхностями. Четырёхугольники состоят из попарно равноудалённых прямых. Называют их боковыми гранями призмы. Оставшиеся же 2 многоугольника — основанием. По сути, фигура — это частный случай некругового цилиндра.
Кроме основания и граней, в состав стереофигуры входит:
- высота — прямая, перпендикулярная плоскостям, лежащим у основания многогранника;
- боковые рёбра — стороны, являющиеся общими для боковых граней;
- вершины — точки, принадлежащие сразу двум отрезкам и формирующим периметр геометрического тела;
- диагонали — отрезки, проходящие через 2 вершины, но при этом несвойственные одной грани;
- диагональные плоскости — пересекающие боковые рёбра и диагональ у основания.
Кроме этого, используются такие понятия, как диагональное и ортогональное сечение. Первое представляет собой параллелограмм, полученный при пересечении призмы и диагональной плоскости. Второе же — пересечение многогранника с плоскостью, перпендикулярной боковому ребру.
В зависимости от расположения стенок и вида основания, призмы разделяют на 3 типа. Прямой называют ту, где все грани — прямоугольники. Если у фигуры в основании находится правильный многоугольник, стереофигура считается правильной. Частным случаем её является полуправильная призма. В ней боковые грани образуют квадраты. Когда же у многогранника основания непараллельные, призму называют усечённой.
Полуправильный многогранник, имеющий 2 параллельных основания в виде правильных n-угольников, равных между собой, чьи грани представляют собой ломаную линию, называют антипризмой. В качестве примера такой фигуры можно привести октаэдр, икосаэдр и восьмиугольный октагон.
Свойства шестигранника
Правильную шестиугольную призму принято обозначать большими латинскими буквами: ABCDEFA1B1C1D1E1F1. Длину основания подписывают маленьким символом a, а длину боковой стороны h. К характеристикам фигуры относят площади основания, боковые грани, полную поверхность, объём многогранника. Всего у геометрического тела 8 граней, 18 рёбер и 12 вершин.
Для успешного вычисления различных параметров фигуры понадобится знать следующие формулы:
- Площадь основания. Так как в основе тела лежат правильные шестиугольники, то, используя их свойства, можно получить формулу: S = (3 * a 2 * √ 3) / 2, где: а — сторона многоугольника.
- Площадь полной поверхности. Определяется она из равенства: Sb = 6 * a * h + 2 * (3 * a 2 * √ 3) / 2. Из-за того, что площадь плоскости можно получить путём сложения сторон призмы и двух поверхностей её основания, а грань — прямоугольник (S прямоугольника = a * h), то указанная формула будет верной.
- Объём. Он равняется произведению площади основания на высоту. Роль последней может играть ребро любой стороны, например, BB1. Учитывая сказанное, формулу можно записать так: V = S * BB 1 = ((3 √ 3) / 2) * (a2 * h).
Если рассмотреть правильный шестиугольник, лежащий в основе призмы ABCDEF, и провести отрезки AB, CD, EF, у них будет общая точка пересечения. Для удобства обозначить её можно буквой O. Так как, в соответствии со свойствами, треугольники AOB, BOC, COD, DOE, EOF, FOA будут правильными, можно составить равенство: AO = OD = EO = OB = CO = OF = a .
Через точку М можно провести прямую AC и CF. Образованный ранее треугольник AEO будет равнобедренным. В нём отрезок AO равняется по величине OE. Значит, угол EOA будет развёрнутым и равняться 120 градусам. Используя свойства равнобедренного треугольника, можно записать: AE = a * √2 * (1 — cos EOA). То есть: AE = AC = √3 * a.
По аналогии можно найти и стороны: EA1, FB1, AC1, BD1, CE1, DF1. Так как AA1 = h, а из свойств правильной призмы следует, что угол EAA1 — прямой, длины сторон будут равны между собой, и их можно найти, используя формулу: √(AA12 + AE2)= √(h2 + 3 * a) = 2 * a. Грань EB1 = FC1 = AD1 = BE1 = CF1 = DA1 = √(BB12 + BE2) = √(h2 + 4 *a) = √5 *a. Сторона FE1 = √(FE2 + EE2) = √(h2 + a2) = √2 *a.
Длины диагоналей призмы равняются сумме квадратов высоты и длины основания под корнем. Это легко доказать, если принять, что ЕЕ1 = h, а FE = a. Треугольник FEE1 прямоугольный, значит, FE = √(h2 + a2), что и следовало доказать.
Решение простого примера
Такого вида задачи обычно даются в учебниках по геометрии для выпускных классов средней школы. Решить их самостоятельно несложно, нужно только знать формулы и представлять, как выглядит та или иная фигура. При этом часто приходится использовать дополнительные построения. Вот один из таких типовых примеров.
Пусть имеется девятиугольная фигура, в которую вписана правильная шестиугольная призма со стандартным обозначением вершин. Сторона основания в ней составляет 4 см, а длина бокового ребра меньше её в 2 раза, то есть равняется 2. Необходимо вычислить расстояние от точки C1 до прямой, соединяющей вершины EF. По условию задачи в основании лежит геометрическое тело, у которого все стороны и углы равны, то есть фигура правильная.
Чтобы понять, что будет представлять искомая прямая, нужно изобразить призму на рисунке и на нём же начертить отрезок. Фактически это будет перпендикуляр, который и является вычисляемым расстоянием. Проекцией точки С1 будет вершина С. Из неё можно построить перпендикуляр, который ограничится точкой E. Таким образом, поставленная задача сводится к поиску длины отрезка C1E.
Найти длину прямой можно как гипотенузу прямоугольного треугольника С1СE. Треугольная фигура будет с прямым углом C. Из условия задачи отрезок С1С в два раза меньше ребра основания, а значит равен 2. Теперь осталось найти, чему равняется длина CE. Геометрическое тело CDE является равнобедренным. По условию CD = ED. Сумму углов шестиугольника можно найти по формуле е = 180 * (n — 2) = 180 * 4 = 720. Получается, что на каждый угол приходится по 120 градусов.
С вершины D можно опустить перпендикуляр DN на CE. Принимая во внимание свойства равнобедренного треугольника, высота DN будет медианной и биссектрисой. Следовательно, угол C равняется 30 градусов, так как CDH — прямоугольный.
Теперь можно найти СH. Сделать это возможно через косинус угла C: cos 30 = CH / CD. Отсюда: CH = 4 * p/2 = 2 √ 3. Так как CH = HE, сторона CE = 2 * 2 √3. К треугольнику CC1E можно применить теорему Пифагора: C1E2 = C1C2 + CE = 22 + (4 c3) 2. C1E2 = √ 52. Таким образом, искомый ответ можно записать так: C1E = 2√13.
Задача высокого уровня
Решение примеров повышенного уровня сложности предполагает не только хорошее понимание изучаемого материала, но и знание предыдущих тем. Понадобится вспомнить формулы для нахождения площадей и объёмов плоских фигур и их свойства. Вот пример одной из таких задач.
Пусть имеется шестиугольная объёмная фигура, у которой баковая грань равняется 6, а площадь основания 12. Нужно найти объём геометрического тела с вершинами в точках A, B1, C1, D1, E1, F1.
В таких задачах перед тем как непосредственно приступить к вычислениям, желательно использовать вспомогательный рисунок. На нём нужно изобразить фигуру в трёхмерной системе координат и подписать все её вершины.
Согласно условию, площадь основания Sabcde1f1 = 12, отрезок AA1 = 6. Так как фигура правильная, то все ребра у призмы буду равны. Чтобы найти, сколько будет составлять объём, понадобится обозначить многогранник. Для этого следует построить отрезки F1B, F1A, B1, E1A, D1A, C1A. Получившаяся фигура представляет собой пирамиду.
Формула для нахождения объёма пирамиды записывается так: V = h * S / 3. Её можно привести к виду: V = (AA1 * Sb1c1d1e1f1) / 3. Теперь нужно определить, чему же будет равняться площадь шестиугольника. Так как в основании призмы лежит правильная фигура с шестью углами, радиус описанной окружности будет совпадать с боковой стороной.
Таким образом, искомая площадь будет равняться шести поверхностям правильного треугольника. В свою очередь, его занимаемый размер можно определить как Sтр = (a * b) * sin / 2. Значит, площадь основания призмы равна: S = (6 * R * R * sin 60) / 2. Подставив заданное условием значение из формулы, можно выразить радиус: R2 = (12 * 2) / 3 √ 3 = 8 /√3.
Площадь треугольника A1B1F1 находится как произведение сторон, умноженное на синус угла и разделённое на 2: S = (a * a * sin120) / 2 = a2 * sin60 / 2 = (R2 * √ 3/3) / 2. Подставив значение R, можно получить: S = (½) * (8 / √ 3) * (√3 / 2) = 2. Тогда площадь пятиугольника будет равняться разнице поверхностей шестиугольника и треугольника A1B1F1, то есть S = 12 — 2 = 10. Теперь можно будет подсчитать и объём пирамиды: Vab1c1d1e1f1 = (1 / 3) * 6 * 10 = 20. Задача решена.