Нахождение объема куба: формула и задачи
В данной публикации мы рассмотрим, как можно найти объем куба и разберем примеры решения задач для закрепления материала.
- Формула вычисления объема куба
- Примеры задач
Формула вычисления объема куба
1. Через длину ребра
Объем (V) куба равняется произведению его длины на ширину на высоту. Т.к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.
V = a ⋅ a ⋅ a = a 3

2. Через длину диагонали грани
Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: a=d/√ 2 .

Следовательно, вычислить объем куба можно так:
![]()
Примеры задач
Задание 1
Вычислите объем куба, если его ребро равняется 5 см.
Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см 3 .
Задание 2
Известно, что объем куба равен 512 см 3 . Найдите длину его ребра.
Решение:
Пусть ребро куба – это a. Выведем его длину из формулы расчета объема:![]()
Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.
Решение:
Применим формулу, в которой используется диагональ грани:
Как вычислить объем куба
wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 82 человек(а).
Количество просмотров этой статьи: 562 175.
Куб — трехмерная геометрическая фигура, у которой все ребра равны (длина равна ширине и равна высоте). У куба шесть квадратных граней, которые пересекаются под прямым углом и стороны которых равны. Вычислить объем куба легко — нужно перемножить длину, ширину и высоту. Так как у куба длина равна ширине и равна высоте, то объем куба равен s 3 , где s — длина одного (любого) ребра куба.
Объемы фигур. Объем куба.
Куб — трехмерная геометрическая фигура, у которой все ребра равны (длина равна ширине и равна высоте).
У куба шесть квадратных граней, которые пересекаются под прямым углом и стороны которых равны.
Вычислить объем куба легко – нужно перемножить длину, ширину и высоту. Так как у куба длина равна
ширине и равна высоте, то объем куба равен s 3 ,

где s – длина одного (любого) ребра куба.
Воспользуйтесь онлайн калькулятором для расчета объема куба: объем куба, онлайн расчет.
Для расчета объемов других тел воспользуйтесь этим калькулятором: калькулятор объемов фигур.
Метод 1 из 3: Возведение в куб ребра куба
- Найдите длину одного ребра куба. Как правило, длина ребра куба дана в условии задачи. Если вы
вычисляете объем реального объекта кубической формы, измерьте его ребро линейкой или рулеткой.
Рассмотрим пример. Ребро куба равно 5 см. Найдите объем куба.
Возведите в куб длину ребра куба. Другими словами, умножьте длину ребра куба саму на себя три раза.
Если s — длина ребра куба, то

и, таким образом, вы вычислите объем куба.
Этот процесс аналогичен процессу нахождения площади основания куба (равна произведению длины на
ширину квадрата в основании) и последующему умножению площади основания на высоту куба (то есть,
другими словами, вы умножаете длину на ширину и на высоту). Так как в кубе длина ребра равна ширине и
равна высоте, то это процесс можно заменить возведением ребра куба в третью степень.
В нашем примере объем куба равен:

- К ответу припишите единицы измерения объема. Так как объем – это количественная
характеристика пространства, занимаемого телом, то единицами измерения объема являются кубические
В нашем примере размер ребра куба давался в сантиметрах, поэтому объем будет измеряться в кубических
сантиметрах (или в см 3 ). Итак, объем куба равен 125 см 3 .
Если размер ребра куба дается в других единицах, то и объем куба измеряется в соответствующих
Например, если ребро куба равно 5 м (а не 5 см), то его объем равен 125 м 3 .
Метод 2 из 3: Вычисление объема по площади поверхности
- В некоторых задачах длина ребра куба не дана, но даны другие величины, с помощью которых вы
можете найти ребро куба и его объем. Например, если вам дана площадь поверхности куба, то разделите
ее на 6, из полученного значения извлеките квадратный корень и вы найдете длину ребра куба. Затем
возведите длину ребра куба в третью степень и вычислите объем куба.
Площадь поверхности куба равна 6s 2 ,
где s – длина ребра куба (то есть вы находите площадь одной грани куба, а затем умножаете ее на 6, так
как у куба 6 равных граней).
Рассмотрим пример. Площадь поверхности куба равна 50 см 2 . Найдите объем куба.
- Разделите площадь поверхности куба на 6 (так как у куба 6 равных граней, вы получите площадь
одной грани куба). В свою очередь площадь одной грани куба равна s 2 , где s – длина ребра куба.
В нашем примере: 50/6 = 8,33 см 2 (не забывайте, что площадь измеряется в квадратных единицах — см 2 ,
- Так как площадь одной грани куба равна s 2 , то извлеките квадратный корень из значения площади
одной грани и получите длину ребра куба.
В нашем примере, √8,33 = 2,89 см.
- Возведите в куб полученное значение, чтобы найти объем куба.
В нашем примере: 2,89 * 2,89 * 2,89 = 2,893 = 24,14 см 3 . К ответу не забудьте приписать кубические
Метод 3 из 3: Вычисление объема по диагонали
- Разделите диагональ одной из граней куба на √2, чтобы найти длину ребра куба. Таким образом,
если в задаче дана диагональ грани (любой) куба, то вы можете найти длину ребра куба, разделив
Рассмотрим пример. Диагональ грани куба равна 7 см. Найдите объем куба. В этом случае длина ребра куба
равна 7/√2 = 4,96 см. Объем куба равен 4,963 = 122,36 см 3 .
Запомните: d 2 = 2s 2 ,
где d — диагональ грани куба, s – ребро куба. Эта формула вытекает из теоремы Пифагора, согласно
которой квадрат гипотенузы (в нашем случае диагональ грани куба) прямоугольного треугольника равен
сумме квадратов катетов (в нашем случае ребер), то есть:
d 2 = s 2 + s 2 = 2s 2 .
- Разделите диагональ куба на √3, чтобы найти длину ребра куба. Таким образом, если в задаче
дана диагональ куба, то вы можете найти длину ребра куба, разделив диагональ на √3.
Диагональ куба — отрезок, соединяющий две вершины, симметричные относительно центра куба, равный
(где D — диагональ куба, s – ребро куба).
Эта формула вытекает из теоремы Пифагора, согласно которой квадрат гипотенузы (в нашем случае
диагональ куба) прямоугольного треугольника равен сумме квадратов катетов (в нашем случае один катет –
это ребро, а второй катет – это диагональ грани куба, равная 2s 2 ), то есть
D 2 = s 2 + 2s 2 = 3s 2 .
Рассмотрим пример. Диагональ куба равна 10 м. Найдите объем куба.


Как найти объем куба
Существует 3 основных способа нахождения площади куба. Каждый применяется в зависимости от условия задачи. Рассмотрим каждый из них.
1
Как найти объем куба – способ 1
Самый простой способ нахождения объема куба – возведение в куб одного из его ребер. Так как у куба все 12 ребер равны, то формула выглядит так V=a3 или V=а*а*а. Если в условии дано ребро, вставьте его значение в формулу и получите правильный ответ. Если длина ребра не дана – придется сначала ее найти. Пример: ребро куба равно 5 см. Найти объем. V = a3 = 53 = 125

2
Как найти объем куба – способ 2
Найти объем куба можно при помощи формулы площади поверхности куба: S=6a3. Скажем, площадь поверхности куба = 54 см2. Тогда a2 = 54/6 = 9. а, соответственно = 3. V = 33 = 27 см3.

3
Как найти объем куба – способ 3
В случае, если нам известна диагональ одной из грани (важно помнить, что диагональ не куба, а именно грани), то поделив его на √2, вы получите длину ребра куба, то есть а. После этого, по старой доброй формуле возводим а в куб и получаем правильный ответ.
Куб – это трехмерная фигура, представляющая собой правильный многогранник, все грани которого квадраты. Чтобы найти объем куба достаточно знать только длину его стороны (они у куба равны).
Чтобы найти объем куба можно воспользоваться калькулятором, либо одной из подходящих формул, которые мы приводим ниже.
Содержание:
- калькулятор объема куба
- формула объема куба через ребро
- формула объема куба через диагональ грани
- формула объема куба через периметр грани
- формула объема куба через диагональ куба
- формула объема куба через площадь полной поверхности
- примеры задач
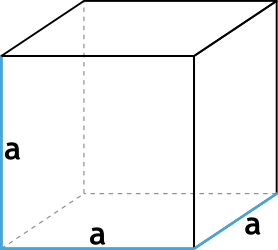
Формула объёма куба через ребро
Формула объёма куба через диагональ грани
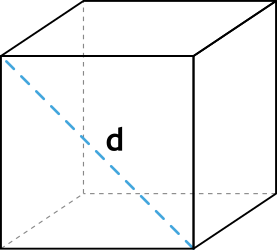
{V = Big( dfrac{d}{sqrt{2}} Big) ^3}
d – диагональ грани куба
Формула объёма куба через периметр грани
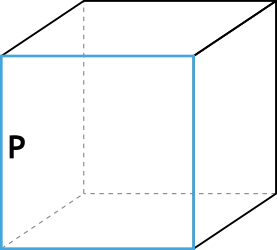
{V= Big( dfrac{P}{4} Big) ^3}
P – периметр грани куба
Формула объёма куба через диагональ куба
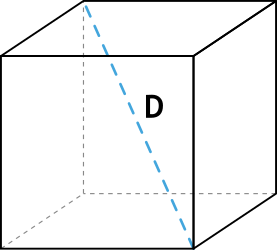
{V= dfrac{D^3}{3sqrt{3}}}
D – диагональ куба
Формула объёма куба через площадь полной поверхности
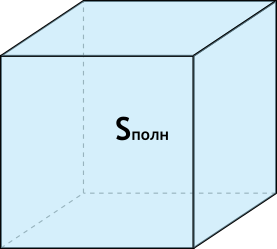
{V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}}}
Sполн – диагональ куба
Примеры задач на нахождение объема куба
Задача 1
Чему равен объём куба с ребром 5 см?
Решение
Для нахождения объема куба, когда известа длина ребра, воспользуемся первой формулой:
V=a ^ 3 = 5 ^ 3 = 125 : см^3
Ответ: 125 см³
Воспользуемся калькулятором для проверки полученного результата.
Задача 2
Найти объем куба, если площадь его поверхности равна 96 см².
Решение
В данном примере нам подойдет эта формула:
V= dfrac{sqrt{{S_{полн}}^3}}{6sqrt{6}} = dfrac{sqrt{{96}^3}}{6sqrt{6}} = dfrac{sqrt{96 cdot 96 cdot 96}}{6sqrt{6}} = dfrac{96 sqrt{96}}{6sqrt{6}} = dfrac{96 sqrt{16 cdot 6}}{6sqrt{6}} = dfrac{96 cdot 4 sqrt{6}}{6sqrt{6}} = dfrac{384 sqrt{6}}{6sqrt{6}} = 64 : см^3
Ответ: 64 см³
Проверить ответ поможет калькулятор .
Также на нашем сайте вы можете найти объем конуса.
Содержание
- Нахождение объема куба: формула и задачи
- Формула вычисления объема куба
- Примеры задач
- Как высчитать кубический метр объёма
- Что такое кубометр
- Перевод в другие единицы
- Пример расчета
- Видео
- Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников
- Объем куба
- Свойства
- Объемы фигур. Объем куба.
Нахождение объема куба: формула и задачи
В данной публикации мы рассмотрим, как можно найти объем куба и разберем примеры решения задач для закрепления материала.
Формула вычисления объема куба
1. Через длину ребра
Объем (V) куба равняется произведению его длины на ширину на высоту. Т.к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.
V = a ⋅ a ⋅ a = a 3

2. Через длину диагонали грани
Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: a=d/√ 2 .

Следовательно, вычислить объем куба можно так:

Примеры задач
Задание 1
Вычислите объем куба, если его ребро равняется 5 см.
Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см 3 .
Задание 2
Известно, что объем куба равен 512 см 3 . Найдите длину его ребра.
Решение:
Пусть ребро куба – это a. Выведем его длину из формулы расчета объема:
Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.
Решение:
Применим формулу, в которой используется диагональ грани:
Источник
Как высчитать кубический метр объёма
Часто приходится задаваться такими вопросами: «А как много нужно чего-нибудь, чтобы наполнить вот это?» Или наоборот: «А сколько этого поместится сюда?» Ведь постоянно приходится что-то куда-то переносить, перекладывать или перевозить, что-то строить, пристраивать или перестраивать. И тут приходится брать в руки обычную или лазерную рулетку и вспоминать единицу измерения объема — кубометр.
Что такое кубометр
Кубический метр — это условная фигура (куб), имеющая длину, ширину и высоту, равную одному метру
Как рассчитать кубический метр, если эти параметры имеют другое значение? Если их произведение (результат перемножения) равно единице, то фигура, которую они составляют, имеет объем один кубометр. Например, объем размерами 1 м ширины, 0,5 м высоты и 2 м длины имеет в себе один кубометр.
В практической деятельности приходится высчитывать объемы различных помещений, и тут можно руководствоваться простой формулой: объем прямого параллелепипеда составляет произведение площади основания на высоту. Комната площадью 32,5 метра и высотой потолков 2,2 метра имеет 71,5 кубометра (куба). Часто помещение имеет наклонный потолок, и тут встает вопрос о высоте. В таком случае можно взять среднее значение этого параметра и получить приблизительный объем.
Если требуется точное значение, то надо помещение мысленно разделить на параллелепипед, имеющий высоту самой низкой стены и подсчитать его объем; затем высчитать объем параллелепипеда, имеющего такую же площадь и высоту, равную разности высот самой высокой и самой низкой стен, поделить пополам и прибавить к объему первого параллелепипеда.
Достаточно часто приходиться рассчитывать объемы различных полостей. Например, при заливке фундамента требуется знать необходимое количество бетонной смеси. Тут все достаточно просто. Точно так же умножаем площадь основания на высоту и получаем искомое значение. Важно вычисления и замер производить в тех единицах измерения, в каких требуется узнать искомое значение. В случае с бетонной смесью ее закупка производится обычно в кубах, поэтому и размеры опалубки под заливку фундамента измеряем в метрах.
Перевод в другие единицы
Для перевода в необходимое значение надо помнить довольно простые пропорции перевода метров в сантиметры и миллиметры.
Единицы длины:
Единицы площади:
- 1 м² = 10 000 см² = 1 000 000 мм²
Единицы объема:
- 1 м³ = 1 000 000 см³ = 1 000 000 000 мм³
Количество жидкости очень часто измеряется в литрах, тут достаточно знать, что:
- 1 л = 1 000 см³
- 1 000 л = 1 м³
Довольно часто приходится рассчитывать объем, исходя из веса, и тут нужно знать плотность вещества. Проще всего с водой, плотность которой 1т/1м³. То есть тонна воды займет один м³ (куб), а тонна молока, например, займет примерно 1,030 куба.
Песок имеет плотность от 1,3 т/м³ до 1,8 т/м³. Это значит, что один м³ весит от 1,3 до 1,8 тонны.
Расчет кубатуры пиломатериалов имеет тонкости. Если доска обрезная и одинаковая, достаточно взять одну, измерить длину, толщину, ширину, перемножить эти параметры, а затем получившееся значение умножить на общее количество. Это и будет искомое значение.
Но при применении необрезной доски, как более доступной по цене, невозможно точно замерить размеры одной единицы, все образцы имеют различные пропорции. В таком случае материал укладывается в штабель с выравненными торцами без перехлеста досок внутри штабеля, и измеряются три параметра всей стопки, перемножаются с применением понижающего коэффициента от 0,5 до 0,7, что и является искомой величиной.
Бывает также, что приходится высчитывать вместимость цилиндрических объектов (бочек, цистерн и подобных). Основанием здесь служит круг, а площадь его равна произведению числа пи (π = 3.14) на квадрат радиуса (половины диаметра) или S=πR².
В практической жизни можно применить и такой достаточно простой способ определения объема жидкостей или сыпучих веществ — в кубометре содержится 1 тыс. литров или 100 десятилитровых ведер. Кому-то покажется хлопотным таскать и пересчитывать ведра с песком или водой, но этот способ точен и общедоступен.
Пример расчета
Допустим, нужно залить ленточный фундамент под сооружение размером 8 на 12 метров, разделенное на три помещения стенами длиной 8 и 6 метров. Примем ширину фундамента 40 см, высоту в метр. Длина составит 54 метра, а объем фундамента будет 0,4*1*54 = 21,6 м³. Это значение можно смело округлить до 22 м³.
Приготовление кубометра бетонной смеси для заливки фундамента требует примерно 350 кг цемента, 800 кг песка, 1200 кг щебня и 140 л воды. Значит, на весь фундамент нужно 154 мешка цемента по 50 кг (7,7 тонн), 17,6 тонн песка, 26,4 тонн щебня и примерно 3 кубометра воды.
Это совершенно приблизительный подсчет, навскидку, позволяющий просто прикинуть размер предстоящих материальных и трудовых затрат. Кстати, количество вынутого под фундамент грунта будет сопоставимо, а то и выше объема самого фундамента, хотя тот и не полностью находится в земле. Объясняется это тем, что траншея под фундамент роется шире для установки опалубки и сопутствующих работ.
Точно так же приходится рассчитывать потребный объем при, допустим, переезде или отправке каких-то товаров или грузов. Ведь переплачивать за лишний объем кузова заказанного автомобиля, транспортного контейнера или железнодорожного вагона никому не хочется.
Достаточно просто вспомнить (посмотреть в интернете) элементарные геометрические формулы из школьной программы и приложить здравый смысл. Ведь всегда можно приблизительно рассчитать объем мебели при переезде или коробок при отправке товара и оценить предстоящие усилия и затраты. А для более точных, окончательных расчетов всегда можно прибегнуть к помощи специалистов. Тем более что предварительный итог более или менее известен, и это может служить некоторой проверкой при согласовании условий.
Видео
Из этого видео вы узнаете, как самостоятельно рассчитать кубатуру.
Источник
Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников
Курс-тренинг Разбираем вариант 97 (1-14) —> Полный цикл видеоуроков по задачам 1-14 —> Полная В-подготовка (задачи 1-14) Полный цикл видеоуроков по задачам 1-14 При каком условии верно равенство 2990 + 1990 + 990 = 3900? —> Новые курсы: «EGE-мастер», «Достойный балл», «Ларинские варианты», «Раз-в-неделю», «Всё включено» —> Постоянно работают курсы для выпускников, учителей и репетиторов
8. Сквозное отверстие в кубе. Ищем объём оставшейся части (вар. 52)
Для каждой грани куба с ребром 6 проделали сквозное квадратное отверстие со стороной квадрата 2. Найдите объем оставшейся части. 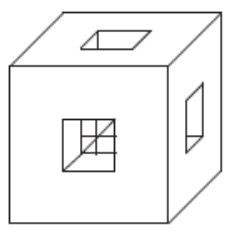
Сторона вырезанного из грани квадрата в три раза меньше ребра куба. 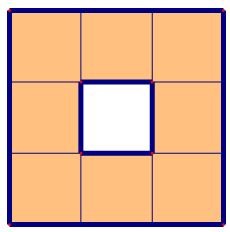 У куба всего шесть граней, из каждой грани мы один квадрат вырезаем. Таким образом, мы удаляем шесть маленьких кубиков из большого куба. После таких операций внутри куба остаётся один невыпиленный кубик. По счёту он седьмой. Представьте себе обыкновенный кубик Рубика. Вот она — удалённая из большого куба часть во всей своей красе:
У куба всего шесть граней, из каждой грани мы один квадрат вырезаем. Таким образом, мы удаляем шесть маленьких кубиков из большого куба. После таких операций внутри куба остаётся один невыпиленный кубик. По счёту он седьмой. Представьте себе обыкновенный кубик Рубика. Вот она — удалённая из большого куба часть во всей своей красе: 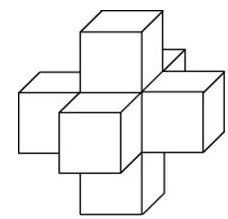 В большом кубе маленьких кубиков ровно 27 (3 · 3 · 3 = 27). После выпиливания отверстия их остаётся 20. Объём каждого маленького кубика равен 8 (2 · 2 · 2 = 8). Объём двадцати кубиков равен 20 · 8 = 160. Ответ: 160
В большом кубе маленьких кубиков ровно 27 (3 · 3 · 3 = 27). После выпиливания отверстия их остаётся 20. Объём каждого маленького кубика равен 8 (2 · 2 · 2 = 8). Объём двадцати кубиков равен 20 · 8 = 160. Ответ: 160
Автор: Ольга Себедаш Просмотров: 20919
Курс-тренинг Разбираем вариант 97 (1-14) —> Полный цикл видеоуроков по задачам 1-14 —> Полная В-подготовка (задачи 1-14) Полный цикл видеоуроков по задачам 1-14 При каком условии верно равенство 2990 + 1990 + 990 = 3900? —> Новые курсы: «EGE-мастер», «Достойный балл», «Ларинские варианты», «Раз-в-неделю», «Всё включено» —> Постоянно работают курсы для выпускников, учителей и репетиторов
Комментарии к этой задаче:
Комментарий добавил(а): ольга
Дата: 2013-11-28
Очень доступно, простым языком изложено объяснение.
Комментарий добавил(а): Надежда
Дата: 2013-12-03
Спасибо Ольга, очень доступно и просто понять. Уметь объяснять — это талант .
Комментарий добавил(а): Наталия
Дата: 2013-11-29
Комментарий добавил(а): Евгений
Дата: 2013-12-02
Комментарий добавил(а): Катерина
Дата: 2013-12-17
Объясните пожалуйста подругому я ничего не поняла
Комментарий добавил(а): egetrener
Дата: 2013-12-17
Катя, возьми в руки кубик Рубика, покрути его, разбери, всё поймёшь.
Комментарий добавил(а): Инкогнито
Дата: 2014-01-20
почему 160 то, обЪем 1 параллипипеда, вырезанного из грани квадрата насквозь (т.к отверстие сквозное) равно 2*2*6=24 т.к таких вырезок 3, а обЪем куба 216 (6*6*6) то получаем обхем части 216-72=144
Комментарий добавил(а): Ольга Себедаш
Дата: 2014-01-20
Инкогнито, центральный кубик вырезаем один раз, а не три.
Комментарий добавил(а): Виктория
Дата: 2014-11-28
Спасибо большое, за хорошее объяснение.
Комментарий добавил(а): LdS
Дата: 2015-02-17
Почему таким методом не получается: Vкуб а*b*c или H^3 (6*6*6)= 216 . Вырезают маленькие кубики объемом (2х2х2) у куба 6 граней т.е (2х2х2)х6 . 216-48=168 .
Источник
Объем куба

Свойства
Куб представляет собой прямоугольный параллелепипед, у которого все ребра равны между собой. Поэтому объем куба вычисляется не просто произведением всех трех его параметров, а возведением ребра куба в третью степень. Поэтому чтобы вычислить ребро куба через объем необходимо извлечь из последнего кубический корень. a=∛V
Площадь грани куба или одной его стороны равна площади квадрата, стороной которого является ребро куба, поэтому кубический корень из объема необходимо возвести во вторую степень. S=∛(V^2 )
Площадь боковой и полной поверхности куба состоят из четырех и шести таких граней соответственно, поэтому их формулы являются аналогией предыдущей с добавлением необходимых коэффициентов. S_(б.п.)=4∛(V^2 ) S_(п.п.)=6∛(V^2 )
Периметр куба равен сумме двенадцати его ребер, равных между собой, поэтому зная, что каждое ребро представлено в виде кубического корня из объема, необходимо умножить его на двенадцать. P=12a=12∛V
Чтобы вычислить диагональ грани куба, нужно вернуться к формуле диагонали квадрата, которым представлены грани. Согласно ей, чтобы найти диагональ, нужно умножить корень из двух на сторону квадрата – ребро куба в данном случае, или кубический корень из объема. d=a√2=∛V √2
Найти диагональ самого куба немного сложнее. Для этого три вершины – диагонали и прилегающего к ней бокового ребра – соединяются в прямоугольный треугольник через диагональ основания, и по теореме Пифагора выводится формула диагонали куба. (рис.2.1) a^2+d^2=D^2 D^2=a^2+2a^2 D^2=3a^2 D=a√3=∛V √3
Чтобы найти радиус сферы, вписанной в куб, через объем, нужно разделить его кубический корень, представляющий собой ребро куба, на два. (рис. 2.2) r=a/2=∛V/2
Радиус сферы, описанной вокруг куба, равен половине диагонали куба, поэтому подставив вместо диагонали необходимую формулу через объем, получим следующее выражение: (рис.2.3) R=D/2=(∛V √3)/2
Источник
Объемы фигур. Объем куба.
Куб — трехмерная геометрическая фигура, у которой все ребра равны (длина равна ширине и равна высоте).
У куба шесть квадратных граней, которые пересекаются под прямым углом и стороны которых равны.
Вычислить объем куба легко – нужно перемножить длину, ширину и высоту. Так как у куба длина равна
ширине и равна высоте, то объем куба равен s 3 ,

где s – длина одного (любого) ребра куба.

Воспользуйтесь онлайн калькулятором для расчета объема куба: объем куба, онлайн расчет.
Для расчета объемов других тел воспользуйтесь этим калькулятором: калькулятор объемов фигур.
Метод 1 из 3: Возведение в куб ребра куба
- Найдите длину одного ребра куба. Как правило, длина ребра куба дана в условии задачи. Если вы
вычисляете объем реального объекта кубической формы, измерьте его ребро линейкой или рулеткой.
Рассмотрим пример. Ребро куба равно 5 см. Найдите объем куба.
Возведите в куб длину ребра куба. Другими словами, умножьте длину ребра куба саму на себя три раза.
Если s — длина ребра куба, то

и, таким образом, вы вычислите объем куба.
Этот процесс аналогичен процессу нахождения площади основания куба (равна произведению длины на
ширину квадрата в основании) и последующему умножению площади основания на высоту куба (то есть,
другими словами, вы умножаете длину на ширину и на высоту). Так как в кубе длина ребра равна ширине и
равна высоте, то это процесс можно заменить возведением ребра куба в третью степень.
В нашем примере объем куба равен:

- К ответу припишите единицы измерения объема. Так как объем – это количественная
характеристика пространства, занимаемого телом, то единицами измерения объема являются кубические
В нашем примере размер ребра куба давался в сантиметрах, поэтому объем будет измеряться в кубических
сантиметрах (или в см 3 ). Итак, объем куба равен 125 см 3 .
Если размер ребра куба дается в других единицах, то и объем куба измеряется в соответствующих
Например, если ребро куба равно 5 м (а не 5 см), то его объем равен 125 м 3 .
Метод 2 из 3: Вычисление объема по площади поверхности
- В некоторых задачах длина ребра куба не дана, но даны другие величины, с помощью которых вы
можете найти ребро куба и его объем. Например, если вам дана площадь поверхности куба, то разделите
ее на 6, из полученного значения извлеките квадратный корень и вы найдете длину ребра куба. Затем
возведите длину ребра куба в третью степень и вычислите объем куба.
Площадь поверхности куба равна 6s 2 ,
где s – длина ребра куба (то есть вы находите площадь одной грани куба, а затем умножаете ее на 6, так
как у куба 6 равных граней).
Рассмотрим пример. Площадь поверхности куба равна 50 см 2 . Найдите объем куба.
- Разделите площадь поверхности куба на 6 (так как у куба 6 равных граней, вы получите площадь
одной грани куба). В свою очередь площадь одной грани куба равна s 2 , где s – длина ребра куба.
В нашем примере: 50/6 = 8,33 см 2 (не забывайте, что площадь измеряется в квадратных единицах — см 2 ,
- Так как площадь одной грани куба равна s 2 , то извлеките квадратный корень из значения площади
одной грани и получите длину ребра куба.
В нашем примере, √8,33 = 2,89 см.
- Возведите в куб полученное значение, чтобы найти объем куба.
В нашем примере: 2,89 * 2,89 * 2,89 = 2,893 = 24,14 см 3 . К ответу не забудьте приписать кубические
Метод 3 из 3: Вычисление объема по диагонали
- Разделите диагональ одной из граней куба на √2, чтобы найти длину ребра куба. Таким образом,
если в задаче дана диагональ грани (любой) куба, то вы можете найти длину ребра куба, разделив
Рассмотрим пример. Диагональ грани куба равна 7 см. Найдите объем куба. В этом случае длина ребра куба
равна 7/√2 = 4,96 см. Объем куба равен 4,963 = 122,36 см 3 .
где d — диагональ грани куба, s – ребро куба. Эта формула вытекает из теоремы Пифагора, согласно
которой квадрат гипотенузы (в нашем случае диагональ грани куба) прямоугольного треугольника равен
сумме квадратов катетов (в нашем случае ребер), то есть:
- Разделите диагональ куба на √3, чтобы найти длину ребра куба. Таким образом, если в задаче
дана диагональ куба, то вы можете найти длину ребра куба, разделив диагональ на √3.
Диагональ куба — отрезок, соединяющий две вершины, симметричные относительно центра куба, равный
(где D — диагональ куба, s – ребро куба).
Эта формула вытекает из теоремы Пифагора, согласно которой квадрат гипотенузы (в нашем случае
диагональ куба) прямоугольного треугольника равен сумме квадратов катетов (в нашем случае один катет –
это ребро, а второй катет – это диагональ грани куба, равная 2s 2 ), то есть
Рассмотрим пример. Диагональ куба равна 10 м. Найдите объем куба.
Источник
В данной публикации мы рассмотрим, как можно найти объем куба и разберем примеры решения задач для закрепления материала.
- Формула вычисления объема куба
- Примеры задач
Формула вычисления объема куба
1. Через длину ребра
Объем (V) куба равняется произведению его длины на ширину на высоту. Т.к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.
V = a ⋅ a ⋅ a = a3

2. Через длину диагонали грани
Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: a=d/√2.

Следовательно, вычислить объем куба можно так:
![]()
Примеры задач
Задание 1
Вычислите объем куба, если его ребро равняется 5 см.
Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см3.
Задание 2
Известно, что объем куба равен 512 см3. Найдите длину его ребра.
Решение:
Пусть ребро куба – это a. Выведем его длину из формулы расчета объема:![]()
Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.
Решение:
Применим формулу, в которой используется диагональ грани:
![]()
