Если пересечь обычную пирамиду (с вершиной) плоскостью, которая параллельна ее основанию, то получится две фигуры: первая (верхняя часть) будет меньшей пирамидой, чем исходная, а фигура, которая лежит между секущей плоскостью и основанием исходной пирамиды, получила название усеченной пирамиды.
Онлайн-калькулятор объема усеченной пирамиды
Если пересечь пирамиду, являющуюся правильной, то и усеченная пирамида будет правильной, если неправильную – то неправильной.
Высотой усеченной пирамиды является перпендикуляр, проведенный из ее верхнего основания в нижнее (или наоборот).
Формула объема пирамиды
Для того чтобы вычислить объем пирамиды, нужно проделать следующие действия:
- Сложить площади обоих оснований пирамиды.
- Возвести произведение этих площадей в степень 1/21/2, то есть извлечь квадратный корень.
- Полученные результаты сложить, затем умножить на высоту пирамиды и разделить на 3.
Формулы имеет такой вид:
V=13⋅h⋅(Sосн 1+Sосн 2+Sосн 1⋅Sосн 2)V=frac{1}{3}cdot hcdot(S_{text{осн 1}}+S_{text{осн 2}}+sqrt{S_{text{осн 1}}cdot S_{text{осн 2}}})
Sосн 1,Sосн 2S_{text{осн 1}}, S_{text{осн 2}} — площади оснований усеченной пирамиды;
hh — высота данной пирамиды.
Разберем решение задач на эту тему.
Найдите объем усеченной пирамиды, если известно, что площадь ее одного основания равна 30 см230text{ см}^2, а площадь второго в 2 раза больше первого. Высота пирамиды равна 7 см7text{ см}.
Решение
Sосн 1=30S_{text{осн 1}}=30
Sосн 2=2⋅Sосн 1S_{text{осн 2}}=2cdot S_{text{осн 1}}
h=7h=7
Первый этап — нахождения площади второго основания:
Sосн 2=2⋅Sосн 1=2⋅30=60S_{text{осн 2}}=2cdot S_{text{осн 1}}=2cdot 30=60
Второй этап — вычисляем объем по формуле:
V=13⋅h⋅(Sосн 1+Sосн 2+Sосн 1⋅Sосн 2)=13⋅7⋅(30+60+30⋅60)≈309 см3V=frac{1}{3}cdot hcdot(S_{text{осн 1}}+S_{text{осн 2}}+sqrt{S_{text{осн 1}}cdot S_{text{осн 2}}})=frac{1}{3}cdot 7cdot(30+60+sqrt{30cdot 60})approx309text{ см}^3
Ответ
309 см3.309text{ см}^3.
В основаниях пирамиды лежат квадраты со сторонами a=8 смa=8text{ см} и b=6 смb=6text{ см}. Высота усеченной пирамиды имеет длину 10 см10text{ см}. Найти ее объем.
Решение
a=8a=8
b=6b=6
h=10h=10
Найдем площадь первого основания. Это просто площадь квадрата, которую мы вычислим по формуле:
Sосн 1=b⋅b=b2=62=36S_{text{осн 1}}=bcdot b=b^2=6^2=36
Аналогично, площадь второго, нижнего основания:
Sосн 2=a⋅a=a2=82=64S_{text{осн 2}}=acdot a=a^2=8^2=64
Наконец, вычисляем объем по формуле:
V=13⋅h⋅(Sосн 1+Sосн 2+Sосн 1⋅Sосн 2)=13⋅10⋅(36+64+36⋅64)≈493.3 см3V=frac{1}{3}cdot hcdot(S_{text{осн 1}}+S_{text{осн 2}}+sqrt{S_{text{осн 1}}cdot S_{text{осн 2}}})=frac{1}{3}cdot 10cdot(36+64+sqrt{36cdot 64})approx493.3text{ см}^3
Ответ
493.3 см3.493.3text{ см}^3.
Профильные эксперты сайта помогут вам выполнить контрольную работу на заказ, скорее оформляйте заказ!
Версия для печати и копирования в MS Word
1
От треугольной пирамиды, объем которой равен 70, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
2
От треугольной пирамиды, объем которой равен 100, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
3
От треугольной пирамиды, объем которой равен 40, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
4
Объём треугольной пирамиды равен 94. Через вершину пирамиды и среднюю линию её основания проведена плоскость (см. рис.). Найдите объём отсечённой треугольной пирамиды.
5
От треугольной пирамиды, объем которой равен 34, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
6
От треугольной пирамиды, объем которой равен 56, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
7
От треугольной пирамиды, объем которой равен 38, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
8
От треугольной пирамиды, объем которой равен 90, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
9
От треугольной пирамиды, объем которой равен 30, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
10
От треугольной пирамиды, объем которой равен 92, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
11
От треугольной пирамиды, объем которой равен 66, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
12
От треугольной пирамиды, объем которой равен 44, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
13
От треугольной пирамиды, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
14
От треугольной пирамиды, объем которой равен 82, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
15
От треугольной пирамиды, объем которой равен 96, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
16
От треугольной пирамиды, объем которой равен 10, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
17
От треугольной пирамиды, объем которой равен 28, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
18
От треугольной пирамиды, объем которой равен 86, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
19
От треугольной пирамиды, объем которой равен 14, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
20
От треугольной пирамиды, объем которой равен 80, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
21
От треугольной пирамиды, объем которой равен 22, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
22
От треугольной пирамиды, объем которой равен 68, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
23
От треугольной пирамиды, объем которой равен 48, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
24
От треугольной пирамиды, объем которой равен 24, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
25
От треугольной пирамиды, объем которой равен 20, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
26
От треугольной пирамиды, объем которой равен 72, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.
Как рассчитать объем усеченной пирамиды
На данной странице калькулятор поможет рассчитать объем усеченной пирамиды онлайн. Для расчета задайте площадь верхнего и нижнего основания и высоту. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Усеченная пирамида — многогранник, образованный пирамидой и её сечением, параллельным основанию.
Через основания и высоту
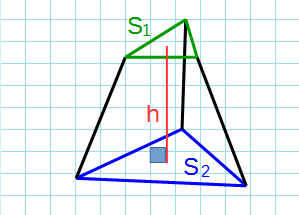
Формула объема усеченной пирамиды через высоту и площадь основания:
S1 – площадь верхнего основания; S2 – площадь нижнего основания; h – высота усеченной пирамиды.
Объем усеченной пирамиды
Рассчитайте объем усеченной пирамиды в зависимости от ее высоты и площадей оснований.
Площадь основания 1
см2
Площадь основания 2
см2
Высота
см
Размерность
Раcсчитать
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
🧮 Что такое калькулятор объема усеченной пирамиды?
Калькулятор объема усеченной пирамиды — это инструмент для расчета объема геометрического тела, которое представляет собой усеченную пирамиду.
Усеченная пирамида — это геометрическое тело, которое состоит из двух параллельных и равных многоугольников, называемых основаниями, и боковой поверхности, состоящей из параллельных трапеций. Объем усеченной пирамиды можно вычислить, зная ее высоту и площади оснований.
Калькулятор объема усеченной пирамиды предоставляет пользователю возможность ввести размеры оснований и высоту усеченной пирамиды, после чего вычисляет ее объем.
Как рассчитывается объем усеченной пирамиды?
Объем усеченной пирамиды можно рассчитать с помощью следующей формулы:
V = (1/3) * h * (A + sqrt(A*B) + B)
где V – объем усеченной пирамиды, h – высота усеченной пирамиды, sqrt – означает квадратный корень, A и B – площади большего и меньшего оснований соответственно.
Для расчета объема усеченной пирамиды необходимо знать высоту и площади ее оснований. Первым шагом необходимо определить площади большего и меньшего оснований. Для этого необходимо найти площадь каждого основания (например, площадь треугольника или многоугольника) и обозначить их A и B соответственно.
Затем необходимо найти высоту усеченной пирамиды, которая является расстоянием между плоскостями оснований. Высоту можно измерить прямым измерением или вычислить, зная расстояние между плоскостями оснований и угол между этим расстоянием и боковой гранью.
После этого можно использовать формулу для расчета объема усеченной пирамиды, подставив известные значения площадей оснований и высоты в формулу.
Для чего можно использовать калькулятор объема усеченной пирамиды?
Калькулятор объема усеченной пирамиды можно использовать для расчета объема данной геометрической фигуры, когда известны ее размеры. Это может быть полезно в различных областях, включая:
- Архитектуру и строительство: расчет объема усеченной пирамиды может быть полезен для расчета объема строительных материалов, таких как бетон или кирпич, необходимых для создания определенных форм.
- Производство: объем усеченной пирамиды может использоваться для расчета объема материала, необходимого для производства определенного изделия.
- Образование: расчет объема усеченной пирамиды может быть использован в качестве учебного материала в школах и университетах для изучения геометрии и математики.
- Хобби и ремесло: расчет объема усеченной пирамиды может быть полезен в различных хобби и ремеслах, таких как создание моделей или изготовление ювелирных изделий.
Усеченная пирамида как фигура
Усеченная пирамида является интересной геометрической фигурой, которая обладает несколькими уникальными свойствами:
- Усеченная пирамида имеет два плоских многоугольных основания, которые могут быть различной формы, но параллельны друг другу.
- В отличие от обычной пирамиды, усеченная пирамида может иметь наклонные боковые ребра, которые делают ее форму более сложной и необычной.
- Усеченная пирамида может использоваться в качестве модели для создания архитектурных конструкций, таких как купола, шатры, крыши зданий и т.д.
- Усеченные пирамиды используются в различных областях науки и техники, включая архитектуру, физику, инженерию, компьютерную графику и многие другие.
- Усеченная пирамида может быть использована как основа для создания различных предметов декора и искусства, таких как светильники, вазы, канделябры и т.д.
- Усеченная пирамида может быть использована для создания различных игрушек и головоломок, что делает ее интересной не только для учебных, но и для развлекательных целей.
❓Вопросы и ответы
Вот некоторые часто задаваемые вопросы и ответы, связанные с калькулятором объема усеченной пирамиды:
Что такое усеченная пирамида?
Усеченная пирамида – это геометрическая фигура, которая имеет два параллельных многоугольных основания и наклонные боковые грани.
Как рассчитать объем усеченной пирамиды?
Объем усеченной пирамиды можно вычислить с помощью специальной формулы: V = (1/3) * h * (S1 + S2 + sqrt(S1 * S2)), где h – высота усеченной пирамиды, S1 и S2 – площади оснований, sqrt – квадратный корень.
Как использовать калькулятор объема усеченной пирамиды?
Введите значения высоты усеченной пирамиды, площадей ее оснований и нажмите кнопку “Вычислить”. Калькулятор автоматически рассчитает объем усеченной пирамиды для вас.
Какие единицы измерения используются при вычислении объема усеченной пирамиды?
Объем усеченной пирамиды может быть выражен в кубических единицах измерения, таких как кубические метры, кубические сантиметры, кубические дюймы и т.д.
Для чего можно использовать калькулятор объема усеченной пирамиды?
Калькулятор объема усеченной пирамиды может быть полезен в образовательных целях, а также для проектирования и расчета объема различных конструкций и изделий.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Введение
Вспомним, что объем пирамиды, как и объем конуса, находятся по формуле ![]() , где
, где ![]() – площадь основания,
– площадь основания, ![]() – высота. Разумеется, в случае конуса площадь основания можно подставить:
– высота. Разумеется, в случае конуса площадь основания можно подставить: ![]() . Теперь перейдем непосредственно к задачам.
. Теперь перейдем непосредственно к задачам.
Пример 1
В правильной треугольной пирамиде ![]() с вершиной
с вершиной ![]() биссектрисы
биссектрисы ![]() пересекаются в точке
пересекаются в точке ![]() ,
, ![]() ,
, ![]() . Найдите длину отрезка
. Найдите длину отрезка ![]() . (См. Рис. 1.)
. (См. Рис. 1.)

Рис. 1. Иллюстрация к условию задачи
Решение. Так как пирамида правильная, то точка ![]() будет проектироваться в центр треугольника
будет проектироваться в центр треугольника ![]() , то есть в точку
, то есть в точку ![]() (точка пересечения биссектрис равностороннего треугольника и есть его центр). Значит, найти надо высоту пирамиды. Мы знаем, что
(точка пересечения биссектрис равностороннего треугольника и есть его центр). Значит, найти надо высоту пирамиды. Мы знаем, что ![]() , откуда
, откуда ![]()
Ответ: ![]() .
.
Пример 2
От треугольной пирамиды ![]() отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды
отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды ![]() и среднюю линию основания
и среднюю линию основания ![]() . Найдите объем отсеченной треугольной пирамиды
. Найдите объем отсеченной треугольной пирамиды ![]() , если
, если ![]() . (См. Рис. 2.)
. (См. Рис. 2.)

Рис. 2. Иллюстрация к условию задачи 2
Решение. Проблема здесь в том, что найти площадь основания и высоту нельзя. Но это и не нужно. Запишем два равенства ![]() и
и ![]() . Заметим, что раз вершина и плоскость основания у новой пирамиды те же, то и высота та же. (См. Рис. 3.)
. Заметим, что раз вершина и плоскость основания у новой пирамиды те же, то и высота та же. (См. Рис. 3.)

Рис. 3. Высота у новой пирамиды и старой одна и та же
То есть чтобы посчитать объем необходимо знать, во сколько раз площадь основания новой пирамиды меньше площади основания исходной. ![]() , т. к.
, т. к. ![]() с коэффициентом подобия
с коэффициентом подобия ![]() . Тогда
. Тогда ![]() .
.
Ответ: ![]() .
.
Пример 3
Во сколько раз увеличится объем правильного тетраэдра ![]() , если все его ребра увеличить в два раза
, если все его ребра увеличить в два раза ![]() ? (См. Рис. 4.)
? (См. Рис. 4.)

Рис. 4. Исходный и увеличенный тетраэдры
Решение. Заметим, что в этом случае площадь основания увеличится в ![]() раза, т. к. исходную сторону
раза, т. к. исходную сторону ![]() увеличили в
увеличили в ![]() раза и получили треугольник со стороной
раза и получили треугольник со стороной ![]() . (См. Рис. 5.). То есть
. (См. Рис. 5.). То есть ![]() .
.

Рис. 5. Основание исходного и увеличенного тетраэдра
Высота тетраэдра также увеличится в ![]() раза. Доказать это можно так: опустим высоту
раза. Доказать это можно так: опустим высоту ![]() и рассмотрим прямоугольный
и рассмотрим прямоугольный ![]() : в нем гипотенуза увеличилась вдвое и катет тоже как радиус описанной окружности около основания. Значит, треугольник перейдет в подобный с коэффициентом
: в нем гипотенуза увеличилась вдвое и катет тоже как радиус описанной окружности около основания. Значит, треугольник перейдет в подобный с коэффициентом ![]() . (См. Рис. 6.) То есть
. (См. Рис. 6.) То есть ![]() .
.

Рис. 6. Треугольник ![]() с коэффициентом подобия
с коэффициентом подобия ![]()
![]() . Раз площадь увеличилась в
. Раз площадь увеличилась в ![]() раза, а высота – в
раза, а высота – в ![]() , то объем увеличится в
, то объем увеличится в ![]() раз
раз ![]() .
.
Ответ: в ![]() раз.
раз.
Пример 4
В сосуде, имеющем форму конуса, уровень жидкости достигает половины высоты ![]() . Объем налитой жидкости
. Объем налитой жидкости ![]() мл. Сколько миллилитров жидкости
мл. Сколько миллилитров жидкости ![]() нужно долить, чтобы полностью наполнить сосуд? (См. Рис. 7.)
нужно долить, чтобы полностью наполнить сосуд? (См. Рис. 7.)

Рис. 7. Иллюстрация к условию задачи 4
Решение. Сначала найдем объем всего сосуда ![]() (в миллилитрах).
(в миллилитрах). ![]() . Объем маленького конуса
. Объем маленького конуса ![]() , тогда искомый объем
, тогда искомый объем ![]() .
.
Заметим, что ![]() с коэффициентом подобия
с коэффициентом подобия ![]() , т. к.
, т. к. ![]() , значит,
, значит, ![]() и
и ![]() .
.
Получаем, что ![]() и
и ![]() , то есть объем большого конуса в
, то есть объем большого конуса в ![]() раз больше объема маленького, заполненного жидкостью.
раз больше объема маленького, заполненного жидкостью.
Тогда объем всего сосуда ![]() мл, а значит, долить надо
мл, а значит, долить надо ![]() мл.
мл.
Ответ: ![]() мл.
мл.
Замечание. Из двух последних примеров можно сделать вывод, что если мы пропорционально увеличим фигуру в ![]() раз, то объем увеличится в
раз, то объем увеличится в ![]() раз.
раз.
Пример 5
Найдите объем ![]() конуса (См. Рис. 8.), если образующая
конуса (См. Рис. 8.), если образующая ![]() и наклонена к плоскости основания под углом
и наклонена к плоскости основания под углом ![]() . В ответе укажите
. В ответе укажите ![]() .
.

Рис. 8. Иллюстрация к условию задачи 5
Решение. Рассмотрим осевое сечение конуса ![]() . Нам известно, что
. Нам известно, что ![]() ;
; ![]() . Тогда из прямоугольного
. Тогда из прямоугольного ![]() :
: ![]() ;
; ![]() (как катет, лежащий напротив угла
(как катет, лежащий напротив угла ![]() ). (См. Рис. 9.)
). (См. Рис. 9.)

Рис. 9. Выносной рисунок осевого сечения
Тогда ![]() .
.
Для записи в ответ ![]() .
.
Ответ: ![]() .
.
Метод объемов в пространстве
Этот метод похож на метод площадей на плоскости. Кратко о сути метода площадей: считаем площадь двумя способами и приравниваем. Например, как найти высоту прямоугольного треугольника со сторонами ![]() ,
, ![]() и
и ![]() , опущенную на гипотенузу? (См. Рис. 10.)
, опущенную на гипотенузу? (См. Рис. 10.)

Рис. 10. Иллюстрация к примеру
Считаем площадь. С одной стороны ![]() , а с другой стороны
, а с другой стороны ![]() . Отсюда
. Отсюда ![]()
То же самое и с объемами: считаем объем двумя способами и находим неизвестную величину.
Пример. Дана правильная треугольная пирамида ![]() , сторона основания
, сторона основания ![]() , а боковое ребро
, а боковое ребро ![]() . (См. Рис. 11.) Найти расстояние
. (См. Рис. 11.) Найти расстояние ![]() от точки
от точки ![]() до плоскости
до плоскости ![]() .
.

Рис. 11. Треугольная пирамида ![]()
Решение. Эту задачу можно решить и «в лоб». Но мы решим так. Заметим, что ![]() . Найдем площадь основания
. Найдем площадь основания ![]() . Теперь найдем высоту
. Теперь найдем высоту ![]() . Рассмотрим прямоугольный
. Рассмотрим прямоугольный ![]() .
. ![]() – радиус описанной около основания окружности, он равен
– радиус описанной около основания окружности, он равен ![]() . (См. Рис. 12.)
. (См. Рис. 12.)

Рис. 12. Длины сторон в прямоугольном ![]()
Тогда по теореме Пифагора ![]() .
.
Получаем, что ![]() .
.
С другой стороны, ![]() . (См. Рис. 13.)
. (См. Рис. 13.)

Рис. 13. Интересующая грань ![]()
Тогда ![]() . Найдем
. Найдем ![]() . Рассмотрим равнобедренный
. Рассмотрим равнобедренный ![]() . Опускаем в нем перпендикуляр на основание и получаем два прямоугольных треугольника с катетом
. Опускаем в нем перпендикуляр на основание и получаем два прямоугольных треугольника с катетом ![]() и гипотенузой
и гипотенузой ![]() . Тогда из египетского треугольника получаем, что высота равна
. Тогда из египетского треугольника получаем, что высота равна ![]() . (См. Рис. 14.)
. (См. Рис. 14.)

Рис. 14. Выносной рисунок грани ![]()
Тогда ![]()
Окончательно: ![]() .
.
Ответ: ![]() .
.
Заключение
Сегодня был решен ряд задач на объемы пирамиды и конуса, мы посмотрели, как работают формулы, выведенные на предыдущем уроке.
Список литературы
- Геометрия. Учебник для 10–11 классов. Атанасян Л.С. и др. 18-е изд. – М.: Просвещение, 2009. – 255 с.
- А.В. Погорелов. Геометрия 11 класс. – М.: Просвещение, 2002.
- Бутузов В.Ф., Глазков Ю.А., Юдина И.И. Геометрия. 11 класс. Рабочая тетрадь. 8-е изд. – М.: Просвещение, 2013. – 78 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Matematikalegko.ru (Источник).
- Matematikalegko.ru (Источник).
- Matematikalegko.ru (Источник).
Домашнее задание
- В основании конуса проведена хорда, которая равна радиусу основания и удалена от центра основания конуса на
 см. Через вершину конуса и эту хорду проведена плоскость, образующая с плоскостью основания угол
см. Через вершину конуса и эту хорду проведена плоскость, образующая с плоскостью основания угол  . Найдите объем конуса.
. Найдите объем конуса. - Найдите объем правильной треугольной пирамиды, если сторона основания равна
 см, а боковое ребро образует с плоскостью основания угол
см, а боковое ребро образует с плоскостью основания угол  .
. - Стороны оснований правильной усеченной треугольной пирамиды равны
 см и
см и  см, а острый угол боковой грани равен
см, а острый угол боковой грани равен  . Найдите объем усеченной пирамиды.
. Найдите объем усеченной пирамиды.
