Как найти объем овала - Сайт, где вы сможете решить свои вопросы

Понятие эллипсоида

Эллипсоид можно получить путем деформации сферы. Проще говоря, эллипсоид — это вытянутая либо сплюснутая сфера.

Онлайн-калькулятор объема эллипсоида

Эллипсоид обладает полуосями. Исходя из того, что эллипсоид — пространственное тело, то полуосей у него будет ровно на единицу больше, чем у эллипса, то есть, три.

Каноническое уравнение эллипсоида может быть записано так:

x2a2+y2b2+z2c2=1frac{x^2}{a^2}+frac{y^2}{b^2}+frac{z^2}{c^2}=1,

где a,b,ca, b, c — полуоси эллипсоида;
x,y,zx, y, z — координаты точек, принадлежащих эллипсоиду.

Полуоси эллипсоида – это положительные величины:

a>0,b>0,c>0a>0, b>0, c>0

Если:

a>b>ca>b>c,

то aa — это большая полуось, bb — средняя, а cc — малая.

Формула объема эллипсоида через его полуоси

Для вычисления объема эллипсоида существует такая формула:

Формула объема эллипсоида через его полуоси

V=43⋅π⋅a⋅b⋅cV=frac{4}{3}cdotpicdot acdot bcdot c

Полезно заметить, что эта формула переходит в формулу для объема шара, если положить:

a=b=c=Ra=b=c=R,

где RR — объем данного шара.

Рассмотрим несколько примеров.

Задача 1

Даны полуоси эллипсоида, численно равные 3 см3text{ см}, 4 см4text{ см}, 5 см5text{ см}. Определите его объем.

Решение

a=3a=3
b=4b=4
c=5c=5

По формуле вычисляем:

V=43⋅π⋅a⋅b⋅c=43⋅π⋅3⋅4⋅5≈251.2 см3V=frac{4}{3}cdotpicdot acdot bcdot c=frac{4}{3}cdotpicdot 3cdot 4cdot 5approx251.2text{ см}^3

Ответ

251.2 см3.251.2text{ см}^3.

Задача 2

Даны две полуоси эллипсоида – 6 см6text{ см} и 8 см8text{ см}. Найдите его объем, если известно, что третья полуось равна длине гипотенузы треугольника, катетами которого являются две вышеописанные полуоси.

Решение

Неважно, как обозначить данные полуоси, поэтому пусть:

b=8b=8
c=6c=6

Для нахождение неизвестной полуоси эллипсоида воспользуемся теоремой Пифагора для прямоугольного треугольника. По условию задачи, неизвестная полуось aa является гипотенузой прямоугольного треугольника, а полуоси bb и cc выступают катетами этого треугольника. Тогда:

a2=b2+c2a^2=b^2+c^2

a2=82+62a^2=8^2+6^2

a2=64+36a^2=64+36

a2=100a^2=100

a=10a=10

Теперь найдем объем эллипсоида по формуле:

V=43⋅π⋅a⋅b⋅c=43⋅π⋅10⋅8⋅6≈2009.6 см3V=frac{4}{3}cdotpicdot acdot bcdot c=frac{4}{3}cdotpicdot 10cdot 8cdot 6approx2009.6text{ см}^3

Ответ

2009.6 см3.2009.6text{ см}^3.

Не знаете, где можно заказать контрольную работу? Наши эксперты окажут вам оперативную помощь в решении контрольных работ по объемам фигур!

Тест по теме “Объем эллипсоида”

Источник

Неравносторонний эллипсоид

Размеры эллипсоида

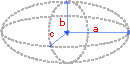
Эллипсоид – поверхность похожая на сферу, у которой сечение выглядит в виде эллипса.

Эллипсоиды

Выражение стандартного эллипсоида в трехмерной системе координат выглядит следующим образом:
${x^2 over a^2}+{y^2 over b^2}+{z^2 over c^2}=1$ ,
где a – радиус по оси x, b – радиус по оси y, c – радиус по оси z.
Объем эллипсоида задается следующей формулой:
Формулу площади поверхности эллипсоида нельзя выразить при помощи простейших фуункций. Кнуд Томсен из Дании предложил следующую приближенную формулу площади поверхности эллипсоида: $Sapprox 4 pi [(a^p b^p + a^p c^p + b^p c^p )/3]^{1over p}$ , где p=1.6075

Эллипсоид

Точность вычисления

Знаков после запятой: 5

Площадь поверхности ( приблизительно)

Сфероид

Если две из трех полуосей эллипсоида равны друг другу, то такой эллипсоид называют сфероидом (эллипсоидом вращения). Различают два вида сфероидов: сплющенный сфероид (похожий на линзу) и вытянутый сфероид (по форме напоминающий сигару).
Объем сфероида любого типа вычисляется по формуле: ${4 over 3}pi a^2 c$

В отличие от эллипсоида, для сфероида известна точная формула для вычисления площади поверхности:

Сплющенный эллипсоид вращения (сфероид)

Для сплющенного сфероида (a = b > c):
$S=2pileft[a^2+frac{c^2}{sin(o!varepsilon)} lnleft(frac{1+ sin(o!varepsilon)}{cos(o!varepsilon)}right)right]$
где угловой эксцентриситет

Вытянутый эллипсоид вращения (сфероид)

Для вытянутого сфероида (a = b < c):
$S=2pileft(a^2+frac{a c o!varepsilon}{sin(o!varepsilon)}right)$
где угловой эксцентриситет

Сфероид

Экваториальный радиус (a=b)

Точность вычисления

Знаков после запятой: 5

Угловой эксцентриситет (в градусах)

Форма Земли похожа на сплющенный сфероид с экваториальным радиусом a ≈ 6,378.137 км и полярным радиусом c ≈ 6,356.752 км. Пользуясь калькулятором можно вычислить площадь поверхности Земли – получается примерно 510 млн. квадратных километров.

Источник

Mensuration is a sub-branch of mathematics that is used to discuss different types of geometrical shapes like cube, cylinder, ellipsoid, their areas, and volume. It is used to find the geometric and algebraic equations that are used to measure various aspects of objects or shapes like Surface Area, Volume, Curve Surface area, etc. In mensuration, volume is used to calculate the amount of space inside a 3D object that can be filled. We can find the volume of any solid object like square, cylinder, ellipsoid, etc. In this article, we will learn how to calculate the volume of the Ellipsoid.

Ellipsoid

Ellipsoid is a three-dimensional geometric figure. It is a closed surface in an elliptical shape and is seen as a structured ellipse. It gets its name from the ellipse because any plane that cuts through the ellipsoid will form an ellipse. It has three axes of rotational symmetry and these three axes are perpendicular to each other and meet at one point which is known as the center of the ellipsoid. Ellipsoid are of two types:

Oblate Ellipsoid: If a = b and a > c, then such type of ellipsoid is known as Oblate ellipsoid.
Prolate Ellipsoid: If a = b and c > a, then such type of ellipsoid is known as a prolate ellipsoid.

The standard equation of ellipsoid is

x²/a² + y²/b² + z²/c² = 1

Here a ≠ b ≠ c. If a = b = c then that ellipsoid is known as a sphere.

Volume of the Ellipsoid

The volume of the ellipsoid is the measurement of the ellipsoid that expresses the amount of three-dimensional space enclosed by a closed surface.

As we know that the equation of ellipsoid be (x²/a²) + (y²/b²) + (z²/c²) = 1 where a, b, c are the lengths of semi-axes of ellipsoid then volume can be calculated by the below formula-

Volume of Ellipsoid = (4/3) × π × a × b × c

The volume of Oblate Ellipsoid is

Volume of Oblate Ellipsoid = (4/3) × π × a × a × b

The volume of Prolate Ellipsoid is

Volume of Prolate Ellipsoid = (4/3) × π × a × b × b

Example:

Given the length of semi-axes are 5cm, 6cm, 4cm

So the volume of the ellipsoid is

V = (4/3) × π × a × b × c

= (4/3) × π × 5 × 6 × 4

= 430/3

= 160

Hence the volume of the ellipsoid is 160

Determining the volume of the ellipsoid

As we know that the equation of ellipsoid is

(x²/a²) + (y²/b²) + (z²/c²) = 1

Let us assume that -a ≤ x ≤ a

Now, we cut the ellipsoid with a plane parallel to the yz-plane

So, we get an ellipse

(y²/b²) + (z²/c²) = 1 – (x²/a²)

(y²/b²(1 – (x²/a²))) + (z²/c²(1 – (x²/a²) )) = 1

So the semiaxes are

p = b√(1 – (x²/a²)) and q = c√(1 – (x²/a²))

As we know that the area of ellipse is

A(x) = πbc(1 – (x²/a²)) …..(1)

Now by using the formula of parent entry we calculate the volume of the ellipsoid

V = limi $int^{a}_{-a}{A(x)} dx$

Now put the value of A(x) for equation (1), we get

V = πbc limi $int^{a}_{-a}{(1-frac{x^2}{a^2})} dx$

V = 4/3πbc

Sample Questions

Question 1: Find the volume of the ellipsoid if the lengths of semi-axes are 3cm, 4cm, 2cm.

Solution:

Given,

Lengths of semi axes of an ellipsoid a=3cm, b=4cm, c=2cm

Volume = (4/3) × π × a × b × c

= (4/3) × π × 3 × 4 × 2

= 32 × π

= 100.53 cm³

So, volume of ellipsoid with given measurements is 100.53cm³.

Question 2: Find the volume of the ellipsoid if the lengths of semi-axes are 5cm, 3cm, 2cm.

Solution:

Given,

Lengths of semi axes of an ellipsoid a = 5cm, b = 3cm, c = 2cm

Volume = (4/3) × π × a × b × c

= (4/3) × π × 5 × 3 × 2

= 40 × π

= 125.66 cm³

So, volume of ellipsoid with given measurements is 125.66cm³.

Question 3: Find the volume of the ellipsoid if the lengths of axes are 6cm, 4cm, 2cm.

Solution:

Given,

Lengths of axes of an ellipsoid are 6cm, 4cm and 2cm.

Length of semi axes = Length of axes/2

a = (6/2) = 3cm

b = (4/2) = 2cm

c = (2/2) = 1cm

Volume = (4/3) × π × a × b × c

= (4/3) × π × 3 × 2 × 1

= 8× π

= 25.13 cm³

So, volume of ellipsoid with given measurements is 25.13cm³.

Question 4: Find the volume of the ellipsoid if the lengths of axes are 12cm, 6cm, and 2cm.

Solution:

Given,

Lengths of axes of an ellipsoid are 12cm, 6cm and 2cm.

Length of semi axes = Length of axes/2

a = (12/2) = 6cm

b = (6/2) = 3cm

c = (2/2) = 1cm

Volume = (4/3) × π × a × b × c

= (4/3) × π × 6 × 3 × 1

= 24× π

= 75.4 cm³

So, the volume of ellipsoid with given measurements is 75.4cm³.

Question 5: Find the volume of ellipsoid if the equation is given as (x²/7²) + (y²/4²) + (z²/2²) = 1

Solution:

Given,

Equation of ellipsoid, (x²/7²) + (y²/4²) + (z²/2²) = 1

It is of form (x²/a²) + (y²/b²) + (z²/c²) = 1

From this we can derive lengths of semi axes.

a = 7

b = 4

c = 2

Volume = (4/3) × π × a × b × c

= (4/3) × π × 7 × 4 × 2

= (224/3) × π

= 234.57 cm³

So, the volume of ellipsoid with given measurements is 234.57cm³.

Last Updated :
03 Jan, 2023

Like Article

Save Article

Источник

Эллипсоид не является телом вращения, тем не менее, его поверхность можно представить в виде алгебраического уравнения второго порядка, что дает возможность вывести формулу его объема через полуоси эллипсоида a, b и c, которые в трехмерной системе координат ложатся на оси x, y и z соответственно. Поскольку эллипсоид берет свое происхождение от сферы, то можно провести закономерную связь между их объемами. Более того, одна формула вытекает из другой и они являются повторением друг друга с различными заданными переменными, с той лишь разницей, что у сферы все три полуоси равны между собой и представлены радиусом окружности, которая вращается вокруг своей оси. Сплюснув окружность в двух направлениях, мы получим эллипсоид, у которого полуоси различны. Заменив каждый радиус в формуле объема сферы на полуоси эллипсоида, получим формулу его объема через полуоси:

Источник

Объём эллиптического (овального) цилиндра

Главная
/
Математика
/
Геометрия
/
Объём эллиптического (овального) цилиндра

Чтобы посчитать объём эллиптического (овального) цилиндра воспользуйтесь нашим онлайн калькулятором:

Онлайн калькулятор

Длинная

Короткая

Высота цилиндра

h =

Результат:
Объём овального цилиндра

V_оц =

Округление ответа: Округление числа π:

Просто введите данные и получите ответ.

Теория

Объём эллиптического цилиндра через полуоси

Чему равен объём овального цилиндра V_оц, если известны его высота h, длинная и короткая полуоси (R и r)?

Формула

V_оц = π⋅h⋅R⋅r

Пример

К примеру, посчитаем объём овального (эллиптического) цилиндра, у которого длинная полуось R = 4 см, короткая – r = 2 см, высота h = 10 см:

V_оц = 3.14 ⋅ 10 ⋅ 4 ⋅ 2 = 251.2 см³

Объём эллиптического цилиндра через оси

Чему равен объём овального цилиндра V_оц, если известны его высота h, длинная и короткая оси (D и d)?

Формула

V_оц = π ⋅ h ⋅ D ⋅ d4

Пример

К примеру, посчитаем объём овального (эллиптического) цилиндра, у которого длинная ось D = 8 см, короткая – d = 4 см, а высота h = 5 см:

V_оц = 3.14 ⋅ 5 ⋅ 8 ⋅ 44 = 3.14 ⋅ 5 ⋅ 8 = 125.6 см³

См. также

Источник

Онлайн-калькулятор объема эллипсоида

Формула объема эллипсоида через его полуоси

Тест по теме “Объем эллипсоида”

Неравносторонний эллипсоид

Эллипсоид

Сфероид

Сфероид

Volume of the Ellipsoid

Sample Questions

Объём эллиптического (овального) цилиндра

Онлайн калькулятор

Теория

Объём эллиптического цилиндра через полуоси

Формула

Пример

Объём эллиптического цилиндра через оси

Формула

Пример

См. также

Вам также может понравиться

Как найти коэффициент прибывших

Как исправить разные ребра

Как найти гипотезу в научной статье

Добавить комментарий Отменить ответ