Условие задачи:
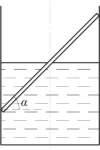Палочка массы (m) наполовину погружена в воду, как показано на рисунке. Угол наклона палочки к горизонту (alpha). С какой силой давит на стенку цилиндрического сосуда верхний конец палочки? Трением пренебречь.
Задача №3.3.56 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(m), (alpha), (P-?)
Решение задачи:
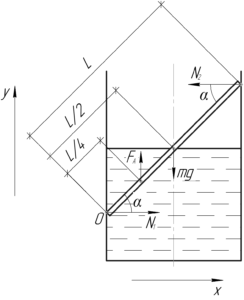Сила давления верхнего конца палочки на стенку сосуда (P) численно равна силе нормальной реакции опоры в этой точке (N_2) согласно третьему закону Ньютона.
[P = {N_2}]
Вообще, на палочку действуют четыре силы: сила тяжести (mg), выталкивающая сила воды (F_А) (на погруженную часть) и две силы нормальной реакции опоры (N_1) и (N_2).
Палочка находится в равновесии. Запишем первое условие равновесия (первый закон Ньютона) в проекции на обе оси координат и второе условие равновесия (правило моментов) относительно точки O. Полученные равенства запишем в виде такой системы:
[left{ begin{gathered}
{F_А} = mg hfill \
{N_1} = {N_2} hfill \
{F_А} cdot frac{L}{4} cdot cos alpha – mg cdot frac{L}{2} cdot cos alpha + {N_2} cdot L cdot sin alpha = 0 hfill \
end{gathered} right.]
Из последнего равенства выразим (N_2):
[{N_2} = frac{1}{2}mg cdot ctgalpha – frac{1}{4}{F_А} cdot ctgalpha ]
Первое равенство системы говорит о том, что ({F_А} = mg), поэтому:
[{N_2} = frac{1}{2}mg cdot ctgalpha – frac{1}{4}mg cdot ctgalpha ]
[{N_2} = frac{1}{4}mg cdot ctgalpha ]
Задачу нужно было решить в общем виде, что мы и сделали. Обратите ваше внимание, что так как ({N_1} = {N_2}) (второе равенство в системе), значит давление нижнего конца на стенку такое же, как и давление верхнего конца.
Ответ: (frac{1}{4}mg cdot ctgalpha).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
3.3.55 Палочка массы 400 г наполовину погружена в воду, как показано на рисунке. Угол
3.4.1 На какую высоту поднимается вода в капиллярной трубке диаметром
3.4.2 В капиллярной трубке радиусом 0,5 мм жидкость поднялась на 11 мм. Определить
Спрятать решение
Решение.
Обоснование.
1. Систему отсчёта, связанную с Землёй, будем считать инерциальной (ИСО).
2. Будем считать палочку абсолютно твёрдым телом. Условие равновесия твёрдого тела, которое может вращаться вокруг некоторой оси — равенство нулю суммы моментов всех сил, приложенных к телу, относительно этой оси.
3. Палочка тонкая, поэтому объём погруженной в воду части палочки можно считать прямо пропорциональным длине этой части.
4. Нить тонкая, поэтому можно пренебречь действующей на неё силой Архимеда.
5. Нить лёгкая, поэтому модуль силы натяжения нити в любой её точке одинаков, в частности: 
(см. рисунок в решении).
6. Груз не касается дна сосуда, поэтому на него со стороны этого дна не действует сила реакции.
Перейдем к решению.
1. Покажем на рисунке силы, действующие на палочку и на шарик. На палочку массой M действуют приложенная к её середине сила тяжести 
приложенная к середине погруженной части сила Архимеда 
сила натяжения нити 
и сила реакции оси 
(направление этой силы может быть противоположным, но для решения данной задачи это несущественно).
На шарик массой m действуют сила тяжести 
сила Архимеда 
и сила натяжения нити 
2. Направим ось OX вниз и запишем условие равновесия шарика (второй закон Ньютона) в проекции на эту ось: 
Учтем, что 
и 
где 
— плотность воды, 
— плотность алюминия.
3. Пусть палочка длиной L в равновесном состоянии составляет с горизонтом угол 
Запишем для палочки уравнение моментов относительно её оси вращения O, считая положительным направлением вращения поворот против часовой стрелки:
Учтем, что 
где 
— искомый объём палочки, 
— плотность соснового дерева и 
4. Выражая силу натяжения нити 
и подставляя её в уравнение моментов, получим:
Отсюда
Ответ: 30,6 см3.
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Критерий 1 | |
|
Верно обоснована возможность использования законов (закономерностей). В данном случае: ИСО, материальная точка, условия применения законов Ньютона, модель для силы сухого трения |
1 |
|
В обосновании возможности использования законов (закономерностей) допущена ошибка. ИЛИ Обоснование отсутствует |
0 |
| Критерий 2 | |
| Приведено полное решение, включающее следующие элементы:
I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае: законы сохранения импульса и механической энергии при абсолютно упругом столкновении одинаковых маленьких шариков, а также кинематические и геометрические соотношения); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений величин, используемых в условии задачи, и стандартных обозначений величин, используемых при написании физических законов); III) проведены необходимые математические преобразования и расчёты, приводящие к правильному числовому ответу (допускается решение «по частям» с промежуточными вычислениями); IV) представлен правильный ответ с указанием единиц измерения искомой величины. |
3 |
| Правильно записаны все необходимые положения теории, физические законы, закономерности, и проведены необходимые преобразования. Но имеются один или несколько из следующих недостатков. Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют.
И (ИЛИ) В решении имеются лишние записи, не входящие в решение (возможно, неверные), которые не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.). И (ИЛИ) В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) в математических преобразованиях/вычислениях пропущены логически важные шаги. И (ИЛИ) Отсутствует пункт IV, или в нём допущена ошибка (в том числе в записи единиц измерения величины). |
2 |
| Представлены записи, соответствующие одному из следующих случаев.
Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения данной задачи, без каких-либо преобразований с их использованием, направленных на решение задачи. ИЛИ В решении отсутствует ОДНА из исходных формул, необходимая для решения данной задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. ИЛИ В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. |
1 |
| Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла | 0 |
| Максимальный балл | 4 |
Приготовление палочек: при прописывании палочек в рецепте указывается не количество основы, а длина и диаметр палочки. Следовательно, количество основы необходимо рассчитать.
Палочку можно представить как цилиндр,
значит нам необходимо узнать объем
цилиндра.
,
,
где h – высота цилиндра,
,
– количество основы на одну палочку, при
плотности
;
на количество n:
Приготовление палочек производится по
общим правилам приготовления суппозиториев.
Литература
Основная:
1.Лекционный
материал. 2.Кугач
В.В. Курс лекций по аптечной технологии
приготовления лекарственных форм. –
Витебск, 2010. – С. 216-232. 3. Хишова, О.М.
Практическое руководство по фармацевтической
технологии аптечного изготовления
лекарственных средств для студентов 3
курса очного отделения: пособие/
О.М.Хишова [и др.]. – Витебск: ВГМУ, 2008. –
С. 294-309.
Дополнительная: 1.Государственная
фармакопея Республики Беларусь. Том 1.
– Минск, 2006. – С. 37-39, 262, 290,
631-632.
2.Технология лекарственных форм.
Учебник в 2х томах. Том 1 /под ред. Т. С.
Кондратьевой/. – М., 1991. – С. 312 – 325.
3.Руководство к лабораторным занятиям
по аптечной технологии лекарственных
форм /под ред. Т. С. Кондратьевой/. – М.,
Медицина. – 1986. – С. 176 – 188.
4. Милованова,
Л.Н. Технология
изготовления лекарственных форм:
уч.пособие/
Л.Н.Милованова,
Н.М.Турусова, Е.В.Бабошина;
серия «Медицина для вас». – Ростов н/Д:
«Феникс», 2002. – С. 285-311, 325-328, 332-335.
5. Муравьев, И.А. Технология лекарств:
учебник для фармацевтических факультетов
ВУЗов/ И.А.Муравьев; изд. 3-е, перераб и
доп. – Т.2. – Москва: «Медицина», 1980. -С.
538-553.
6.
Краснюк,
И.И. Фармацевтическая технология.
Технология лекарственных форм: учебник
для фармацевтических факультетов ВУЗов/
И.И.Краснюк, Г.В.Михайлова, Е.Т.Чижова-
Москва: ИЦ «Академия», 2004. – С. 350-357.
7. Елисеев, Ю.Ю. Полный справочник
фармацевта: справочник; под
редакцией Елисеева Ю.Ю. –
М.:«Эксмо-Пресс», 2006 – 768 с.
8. Об утверждении инструкции по
оценке качества лекарственных средств,
изготовляемых в аптеках: Постановление
МЗ РБ № 15 от 23.05.2000 г. – Минск: МЗ РБ, 2000.
9.О контроле качества
лекарственных средств, изготовляемых
в аптеках: Постановление МЗ РБ № 35 от
14.08.2000 г – Минск: МЗ РБ, 2000.
10. О
внесении изменений и дополнений в
постановления Министерства здравоохранения
Республики Беларусь от 27.12.2006 г. № 120 и
от 31.10.2007 г. № 99: Постановление
№ 181 от 31.10.2008 г. –
Минск: МЗ РБ, 2008.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Калькулятор для расчета объема параллелепипеда
C помощью нашего Онлайн-калькулятора для расчета объема параллелепипеда Вы можете быстро и точно рассчитать объем прямоугольного параллелепипеда. Для того, чтобы вычислить объем прямоугольного параллелепипеда, введите значение ребер “a”, “b”, “c” и нажмите кнопку “Рассчитать”. Также Вы можете указать точность полученного результата, т.е. количество знаков после запятой, до которого будет округлен рассчитанный объем параллелепипеда.
Задайте значение ребер параллелепипеда а, b, c и нажмите кнопку “Рассчитать”
Округлить результат до
знаков после запятой
Рассчитать
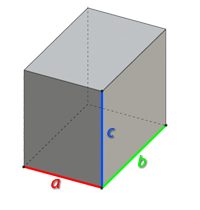
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Объем прямоугольного параллелепипеда вычисляется по следующей формуле:
,
где a, b, c – ребра параллелепипеда.
Как сдеать лабораторную работу?
Знаток
(328),
на голосовании
14 лет назад
Голосование за лучший ответ
Vital
Мастер
(1582)
14 лет назад
Кажется, не хватает входных данных. Если бы была известна масса палочки, тогда было бы достаточно измерить объем вытесненной жидкости (с помощью линейки измерить на какую высоту поднимется жидкость и умножить на площадь основания сосуда) . Либо необходим динамометр, чтобы измерять вес стеклянной палочки. Вес палочки в воздухе будет тяжелее, чем в воде за счет того, что в воде действует сила Архимеда и выталкивает погруженное тело. Если расписать все силы, то можно выяснить и плотность палочки через разность веса палочки в водухе и жизкости, и плотности жидкости.
А в текущей постановке задачи идей нет.
