Напиши формулу объема прямоугольного параллелепипеда. Найди объем прямоугольного параллелепипеда, если:
а) a = 8 см, b = 10 см, c = 9 см;
б) a = 30 м, b = 20 м, c = 70 м;
в) a = 2 дм, b = 70 см, c = 50 см.
(Обрати внимание на единицы измерения!)
reshalka.com
ГДЗ учебник по математике 3 класс Петерсон. 31 урок. Формула объема прямоугольного параллелепипеда. Номер №4
Решение а
V = a * b * c = 8 * 10 * 9 = 80 * 9 = 720
(
с
м
3
)
− объем прямоугольного параллелепипеда.
Ответ: 720
с
м
3
Решение б
V = a * b * c = 30 * 20 * 70 = 600 * 70 = 420000
(
м
3
)
− объем прямоугольного параллелепипеда.
Ответ: 420000
м
3
Решение в
V = a * b * c = 20 * 70 * 50 = 70 * 1000 = 700000
(
с
м
3
)
− объем прямоугольного параллелепипеда.
Ответ: 700000
с
м
3
-
Главная
-
ГДЗ
- 3 класс
- Математика
-
Петерсон. Учебник
- Страница 90. Урок 39. Часть 2
Вернуться к содержанию учебника
Вопрос
Задание № 4. Найди по формуле объём прямоугольного параллелепипеда, если его измерения равны:
а) а = 8 см, b = 10 см, с = 9 см;
б) а = 30 м, b = 20 м, с = 70 м;
в) а = 2 дм, b = 70 см, с = 50 см.
(Обрати внимание на единицы измерения.)
Подсказка
Ответ
Вопрос
Задание № 5. Каркас прямоугольного параллелепипеда сделан из проволоки. Его размеры указаны на рисунке. Сколько проволоки для него потребовалось?
Подсказка
Ответ
Вопрос
Задание № 6. Напиши формулу объёма куба со стороной а. Найди объём куба, если: 1) а = 4 см; 2) а = 60 м; 3) а = 900 см.
Подсказка
Ответ
Вопрос
Задание № 7. Комната имеет форму прямоугольного параллелепипеда. Её высота равна 3 м, ширина 4 м, а длина 7 м. Чему равен объём этой комнаты? Найди площадь её пола, потолка, стен?
Подсказка
Ответ
Вопрос
Задание № 8.
а) Найди сумму площадей всех граней прямоугольного параллелепипеда, если его измерения равны 5 см, 2 см и 3 см.
б) Напиши формулу площади поверхности прямоугольного параллелепипеда с измерениями а, b и с.
в) Напиши формулу площади поверхности куба со стороной а.
Подсказка
Ответ
Вопрос
Задание № 9. Реши уравнения с комментированием и сделай проверку:
| 35 : 4 + 6 = 11 | (4 + х) : 8 = 9 | (9 • t – 14) : 4 = 10 |
Подсказка
Ответ
Вопрос
Задание № 10. При каких значениях а верны равенства? Объясни их смысл.
| а + 0 = 0 + а = а | а : 1 = а | а • 1 = 1 • а = а |
| а – 0 = а | а : а = 1 | а • 0 = 0 • а = 0 |
| а – а = 0 | 0 : а = 0 |
Подсказка
Ответ
Вопрос
Задание № 11. Найди значения выражений:
| а) 375 • 0 + 294 : 294 – (16 – 16) : 2 |
| б) 7 : (15 : 15) – (21 – 21) • 5 + 1 • 9 |
Подсказка
Ответ
Вопрос
Задание № 12. Повару надо зажарить 6 котлет, а на сковородке умещаются только 4 котлеты. Каждую котлету надо жарить 5 мин на одной стороне и 5 мин на другой. За какое минимальное время повар может зажарить все котлеты?
Подсказка
Ответ
Вернуться к содержанию учебника
Конспект урока по «Математике»
3 класс
Тема: «Формула объема прямоугольного параллелепипеда».
Используемые технологии:
• информационно-коммуникативные;
- развивающее обучение;
• технология сотрудничества;
• гуманно-личностные;
Автор: Кошелкина Татьяна Андреевна
учитель начальных классов
ГБОУ школа №212 Фрунзенского района
Санкт-Петербурга
Тип урока: открытие новых знаний.
Тема: «Формула объема прямоугольного параллелепипеда».
Цели:
1)Уточнить представления у учащихся о прямоугольном параллелепипеде и его элементах – ребрах, гранях, вершинах.
2) Познакомить учащихся с кубом как частным случаем прямоугольного параллелепипеда.
3) Познакомить учащихся с формулой объема прямоугольного параллелепипеда.
4) Тренировать навыки устного счета, умения решать задачи на нахождение объема прямоугольного параллелепипеда и куба.
Ход урока:
1. Мотивация к учебной деятельности.
Что вы видите на доске? (формулы)
– Что такое формула? (Формулой называют верное равенство, устанавливающее взаимосвязь между величинами).
– С какими формулами мы вчера работали? (С формулами площади и периметра прямоугольника).
2. Актуализация знаний и фиксация затруднений в пробном учебном действии.
Давайте их повторим, применив при решении задач.
Вычисли, пользуясь формулами:
а) площадь прямоугольника со сторонами 9 м и 40 м;
б) периметр прямоугольника со сторонами 9 м и 10 м
в) сторону прямоугольника, вторая сторона которого равна 20 м, а площадь— 180 м²
г) сторону прямоугольника, вторая сторона которого равна 3см, а периметр- 20 см.
д) объём прямоугольного параллелепипеда с измерениями 6 см, 9 см, 2см;
3. Выявление места и причины затруднения.
Почему не удаётся вычислить объём прямоугольного параллелепипеда? (нет формулы)
Сформулируйте тему урока.
Какую цель мы должны перед собой поставить?
Уточнение представления о плоских и объемных фигурах.
На доске – фигуры:
– Назовите фигуры. (Прямоугольник, параллелепипед, квадрат, куб.)
– На какие группы можно разбить фигуры? (На доске фиксируются слова «Плоские» и «Объемные» фигуры.)
Найдите среди фигур прямоугольный параллелепипед.
Я предлагаю вспомнить всё, об этой фигуре выполнив практическую работу.
Работать будем в группах
– Возьмите в руки модель параллелепипеда и рассмотрите ее. (Учащиеся работают с моделью)
Начнём отвечать на вопросы вместе
– Какими фигурами ограничен параллелепипед? (Прямоугольниками.)
– Назовите отличия данной фигуры от прямоугольника. (Объемная, пространственная.)
– Давайте уточним, какую фигуру называют прямоугольным параллелепипедом?
На доске открывается запись с пропусками:
Прямоугольный параллелепипед – это ______________________ фигура, ограниченная __________________________.
«Прямоугольный параллелепипед – это пространственная фигура, ограниченная прямоугольниками».
– Далее исследование фигуры продолжим в группах. Выполните задание на карточках.
1) Найдите на моделях элементы параллелепипеда, посчитайте и запишите их количество:
граней — ________
вершин — ________
ребер — ________
2) Измерьте длину всех ребер. Запишите все измерения:___________________________________________________________
Сколько различных измерений у вас получилось? Запиши:___________________
При проверке дети на моделях показывают элементы фигуры, все понятия уточняются.
– А куб является параллелепипедом? В чем его особенности? (Куб – это особый параллелепипед, у него равны все ребра и грани; грани являются квадратами.)
Задание для пробного действия.
– Какая величина характеризует параллелепипед в силу того, то это пространственная фигура? (Объем.)
– В математике принято обозначать объем латинской буквой «V»
Что предстоит нам сделать, чтобы мы могли вычислять объём? (Вывести формулу для нахождения объема прямоугольного параллелепипеда.)
4. Построение проекта выхода из затруднения.
Составим план действий.
– Какие данные необходимы для формулы? (Измерения.)
– Где вы будете находить измерения параллелепипеда? (На модели параллелепипеда.)
– Что вам поможет установить связь между измерениями? (Арифметические действия.)
-К какому результату вы должны прийти? (Вывести формулу объема прямоугольного параллелепипеда.)
Учитель на доске фиксирует план действий.
1) Определить по модели параллелепипеда измерения.
2) Выбрать арифметическое действие.
3) Записать формулу для нахождения объёма прямоугольного параллелепипеда
5. Реализация построенного проекта.
Рассмотрите ещё одну модель пр. пар.
Что вы видите?
Выложите кубики на дно данной модели.
Сосчитайте количество кубиков удобным способом.
Что мы нашли? (площадь прямоугольника в основании пр пар)
-Назовите формулу? S = a *b (длину умножить на ширину)
-Какой буквой обозначена длина «а», какой ширина «b», а ещё у параллелепипеда есть высота, обозначим её буквой «с».
– Ребята площадь основания мы нашли, сколько таких оснований будет в параллелепипеде? ( «с» штук)
-И так ребята, чтобы найти площадь основания нужно а*b,
-А чтобы найти объём нужно а*b и умножить на что? (на с)
– Обратитесь к выводам в учебнике на с. 89.
Дети читают вслух правило нахождения объема параллелепипеда.
– Совпал ли ваш вывод с выводом учебника? (Да, мы сделали правильный вывод.)
– Как найти объема параллелепипеда? (V = a • b • с)
На доске фиксируется формула
V = a • b • с
– Формулу объема можно читать разными способами.
Учебник с.90
Что мы с вами сейчас сделали ? (вывели формулу нахождения объёма прямоугольного парал.)
Сможем мы теперь вернуться к задаче, вспомнить, где возникло затруднение и его преодолеть?
Единицы измерения объёма:
6. Первичное закрепление с проговариванием во внешней речи.
Где может нам пригодиться формула?
Попробуем ей воспользоваться
№4 с.90
№5
7. Самостоятельная работа
№ 4 Б) , №5 Б)
9. Рефлексия учебной деятельности на уроке.
– Какую цель вы перед собой ставили? (…)
– Достигли цели? Докажите. (Мы открыли формулу объема параллелепипеда.)
– Вспомним формулу. (Дети проговаривают еще раз V = a • b • с)
– Научились ли использовать новый способ?
Урок математики в 3 классе « Формула объема прямоугольного параллелепипеда»
Никаньшина Н.И., учитель начальных классов,
МБОУ « Гимназия №102 им.М.С.Устиновой», г.Казань, РТ
Цели: – углубить и расширить знания о применении формул в математике;
– познакомить с формулой объема прямоугольного параллелепипеда;
– совершенствовать вычислительные навыки;
– развивать математическую речь.
Планируемые результаты: учащиеся научатся находить объем прямоугольного параллелепипеда по формуле; понимать учебную задачу урока и стремиться к ее выполнению; осуществлять самоконтроль и самооценку, взаимоконтроль; слушать собеседника и вести диалог.
Ход урока
I.Организационный момент.
Сегодня настроение хорошее с утра? (Да)
Друг друга видеть рады? (ДА)
Готовы считать, размышлять, узнать? (Да)
А пятерки получать? (да)
Сегодня предлагаю вам самостоятельно оценивать каждый этап урока и закрашивать 5! (рисунок 1)
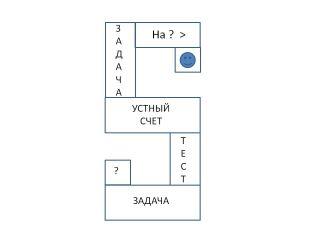
Рисунок 1 Самооценка.
А сейчас разминка для ума!
II. Актуализация знаний.
Устный счет.
Ребята, у вас на столе листочки на которых отмечены точки с цифрами (рисунок 1). Выполните задания математического диктанта, найдите точки с правильным ответами и последовательно соедините их отрезками.
-
(6 +9) • 3 (45)
-
(50ˑ9) +30 (480)
-
(160 – 70) -25 (65)
-
(720:90) •8 (64)
-
Найдите площадь прямоугольника со сторонами 9 и 5 см. (45 кв.см)
-
Найдите периметр квадрата со стороной 12 см. (48 см)
-
Чему равна длина прямоугольника, если его площадь 180 кв. м, а ширина 9м. (20м)
-
Найдите площадь прямоугольника со сторонами 13 и 5 мм. (65 кв.мм)
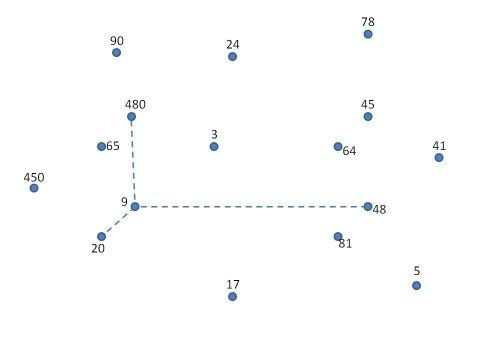
Рисунок 2 Устный счет.
III.Самоопределение к деятельности.
-Какая фигура у вас получилась? (прямоугольный параллелепипед)
-Где в жизни вы встречались с такой фигурой? (коробки, бассейн….)
-Какая это фигура? (объемная)
– Что мы можем вычислить у этой фигуры? (объем)
– Как вычислить объем? (не знаем формулы)
-Кто может сформулировать тему урока?
Формула объема прямоугольного параллелепипеда.
-Какие цели мы поставим? (вывести формулу объема, использовать формулу при решении задач)
– Как мы получили параллелепипед? (соединили точки)
-Выделите точки. Сколько их (8)
-Как они называются? (вершины)
-Из чего состоит поверхность параллелепипеда? (из прямоугольников)
-Как они называются? (грани)
-Сколько их? (6)
-Как называются стороны граней? (ребра)
-Сколько их? (12)-Что интересного заметили? (противоположные грани равны)
-Обведите длинную сторону основания и все равные ей зеленым цветом.
– Обведите короткую сторону основания и все равные ей красным цветом.
– Что лежит в основании прямоугольного параллелепипеда? (прямоугольник)
-Закрасьте его.
– Что можем измерить у прямоугольника? (длину и ширину)
– Что можем найти? (площадь)
– А что еще есть у параллелепипеда, что мы не обвели? (высота)
– Кто уже догадался, как найти объем?
a ˑ b ˑ c = V
-
Первичное закрепление.
-Можем сейчас найти объем получившегося параллелепипеда? (да)
– Что мы должны сделать? (измерить длину, ширину, высоту и перемножить)
Работа в тетрадях.
а = 6см
b = 2 см
c = 3см
V = ? V = 6 • 2 • 3=36 (куб.см)
– В каких единицах измеряется V?
V. Физминутка.
Ребята, я сейчас буду показывать карточки с единицами измерения, если это единицы измерения периметра P – 1 раз хлопаем в ладоши, если S – ходьба на 1и2, если V – 3 прыжка. (см, кв.дм, куб.м, мм и т.д.).
VI.Закрепление изученного материала.
1.- Ребята, мы немного отдохнули. А где вы любите отдыхать летом? (на реке, на море) А можем мы кусочек моря поместить у себя дома? (да). Как? (в аквариуме)
-Вычислите V аквариумов?
1 вариант а =5дм, в = 4дм, с = 3дм. ( 60 куб.дм)
2 вариант а =6дм, в = 4 дм, с = 7 дм (168 куб.дм)
Дети работают самостоятельно. Проверка в парах.
-Сравните на сколько один аквариум больше другого. (работа в парах)
168-60=108 (куб.дм)
– Кого можем поселить в 1 аквариум? (черепашку, рыбок), а во второй? (хамелеона). Чем мы должны заполнить аквариум для рыбок? (водой)
2.С понятием V вы еще часто будете встречаться. Игра «Выдумка» (ребята читают 3 высказывания и ищут среди них выдумку).
– Объем памяти человека гораздо больше объема памяти самого современного компьютера.
– Оранжевый цвет визуально увеличивает объем предметов.
– Объем луны больше объема воды в Тихом океане.
(ложь 3 ,они равны)
3.Самостоятельная работа.
1.Ученые проводят много экспериментов. А вы хотите побывать в роли экспертов?(да)
Задача: Согласно санитарным нормам в классе на 1 ученика должно приходиться 5 куб. метров воздуха. Соответствует ли норме количество учеников нашего класса, если ширина кабинета 8м, длина 6м, высота 4м?
V = 6 • 8 •4 = 192 куб.м
192 : 32 =6куб.м
6 5 соответствует
3. Тест
1) Сколько у прямоугольного параллелепипеда вершин, граней,ребер?
а) 8, 6, 12
б) 6, 8, 12
в) 12, 8 ,6
2) Найди формулу объема
а) (а + в)• 2
б) а• в
в) а • в • с
3) В каких единицах измеряется объем?
а) см
б) кв.см
в) куб.см
4)Найдите объем прямоугольного параллелепипеда со сторонами 8м,6м,10м.
а) 480 м
б)480 куб.м
в) 4800 куб.м
5) Найдите объем фигуры со сторонами 30 дм,20дм,50дм.
а)30000куб дм
б)3000 куб.дм
в) 3000л
VII. Рефлексия.
-Кто полностью закрасил поверхность 5? (на каждом этапе урока после проверки ребята закрашивали ту часть 5 , где было отмечено задание). Не закрашенные участки показывают, над чем вам еще нужно поработать.
– Раньше я думал что……, теперь думаю.
VIII. Домашнее задание.
Составить и решить задачу на нахождение объема.
7
Урок 31.
Л.Г.Петерсон. Математика. 3 класс: Методические рекомендации.
–М: Издательство «Ювента»,2008.
Математика. 3 класс. Часть2.- М: Издательство «Ювента»,2008.
Тип урока: открытие новых знаний.
Тема: «Формула объема прямоугольного параллелепипеда».
Автор: Золотова Елена Николаевна – учитель начальных классов КОГОАУ «Многопрофильный лицей» (г. Вятские Поляны)
Основные цели:
1)Уточнить представления у учащихся о прямоугольном параллелепипеде и его элементах – ребрах, гранях, вершинах.
2) Познакомить учащихся с кубом как частным случаем прямоугольного параллелепипеда.
3) Познакомить учащихся с формулой объема прямоугольного параллелепипеда.
4) Тренировать навыки устного счета, умения решать задачи на нахождение объема прямоугольного параллелепипеда и куба.
Мыслительные операции, необходимые на этапе проектирования: анализ,сравнение, аналогия, обобщение.
Ход урока:
1. Мотивация к учебной деятельности.
Цель:
1) создать условия для возникновения внутренней потребности включения в учебную деятельность через загадку;
2) актуализировать требования к ученику со стороны учебной деятельности;
3) установить тематические рамки урока: знакомство с формулой объема прямоугольного параллелепипеда.
Организация учебного процесса на этапе 1:
– Что такое формула? (Формулой называют верное равенство, устанавливающее взаимосвязь между величинами).
– С какими формулами познакомились? (С формулами площади и периметра прямоугольника).
-Запишите формулу, как найти периметр прямоугольника.
-Запишите формулу, показывающую, как найти сторону прямоугольника по его периметру и другой стороне.
-Запишите формулу, как найти периметр квадрата.
-Какие формулы вы ещё помните. Назовите.
– Как вы думаете, со всеми ли формулами вы познакомились? (…)
– Хотите узнать больше? (Да.)
– В какой теме вы продолжите делать открытия? (В теме «Формулы».)
Прикрепить карточку с темой «Формулы» на доску.
-Чем формулы отличаются от уравнений? (В уравнениях буквы обозначают некоторые числа, а в формулах – значения величин; формулы верны для всех значений букв, а уравнения только для корней)
– Расскажите, что вас ожидает во время открытий? (Сначала мы повторяем необходимое, потом будет задание на пробное действие. Мы постараемся его выполнить и, наверное, не получится. Мы подумаем, почему не получилось, поставим цель, составим план действий и, работая по плану, откроем новый способ…)
– Итак, отправляемся за новыми знаниями.
2. Актуализация знаний и фиксация затруднений в пробном учебном действии.
Цель:
1) актуализировать знания о свойствах умножения, о формулах площади и периметра прямоугольника и их единицах измерения, представления о видах фигур (плоских и объемных);
2) тренировать вычислительные навыки;
3) уточнить представление учащихся о параллелепипеде и кубе;
4) тренировать вариативность мышления, мыслительные операции: сравнение, анализ, обобщение;
5) мотивировать к пробному действию и его самостоятельному выполнению и обоснованию;
6) организовать выполнение пробного действия и фиксацию затруднения;
7) организовать анализ полученных ответов и зафиксировать индивидуальные затруднения в выполнении пробного действия или его обосновании.
Организация учебного процесса на этапе 2:
– Что вы должны сделать в начале пути? (Повторить материал, необходимый для открытия нового.)
1) Математический диктант. (Работа на карточках)
– Вычислите удобным способом.
а) 360 – 97 + 97;
б) 18 + 19 + 20 + 21 + 22;
в) 562 – (462 + 60);
г) (20 + 8) · 4;
д) 2 · 19 · 5;
е) 16 · 3 + 24 · 3.
Проверка. Учащиеся называют ответы.
– Какими свойствами умножения воспользовались при вычислениях?
На доске появляются соответствующие эталоны
(а + в ) ·с = а ·с + в ·с
а · в · с = а ·(в· с)
– Ответы примеров расположите в порядке возрастания и соотнесите с буквами.
На доске появляется запись:
360 – А; 100 – И; 40 – Ф; 112 – Г; 190 – Р; 120 – У (Получается слово «Фигура».)
2) Уточнение представления о плоских и объемных фигурах.
Н а доске – фигуры:
– Назовите фигуры. (Прямоугольник, параллелепипед, квадрат, куб.)
– На какие группы можно разбить фигуры? (На доске фиксируются слова «Плоские» и «Объемные» фигуры.)
– Поработаем с плоскими фигурами.
– Найдите площадь и периметр прямоугольника со сторонами 21 см и 4 см. Не забудьте про наименования!
Учащиеся работают на индивидуальных досках.
– Проверим ваши решения. Чему равна площадь прямоугольника? (84 см2.)
Если допущены ошибки, то их обязательно надо разобрать.
– Какой формулой воспользовались для нахождения площади прямоугольника?
На доске фиксируется формула S = a · b.
– Назовите единицы измерения площади в порядке возрастания.
На доске появляется эталон
Площадь
Единицы измерения площади:
мм2, см2, дм2, м2
– Чему равен периметр прямоугольника? (50 см)
– Какой формулой воспользовались для нахождения периметра прямоугольного прямоугольника? Озвучьте ее.
На доске появляется эталон Р = (а + в)·2; Р = а·2 + в· 2.
– Назовите единицы измерения периметра прямоугольного прямоугольника в порядке убывания. (м, см, дм, м)
Периметр
Единицы измерения периметра:
мм, см, дм, м
На доске появляется эталон
– Чем являются аив в данных формулах? (Измерениями прямоугольника: длиной и шириной.)
3) Уточнение представления о прямоугольном параллелепипеде и кубе.
– Поработаем с объемными фигурами.
Учитель показывает на параллелепипед
– Как называется данная фигура? (Прямоугольный параллелепипед.)
– Назовите отличия данной фигуры от прямоугольника. (Объемная, пространственная.)
На доске появляется слово «Пространственная».
– Возьмите в руки модель параллелепипеда и рассмотрите ее. (Учащиеся работают с моделью, изготовленной дома.)
– Какими фигурами ограничен параллелепипед? (Прямоугольниками.)
На доске появляется слово «Прямоугольники».
– Давайте уточним, какую фигуру называют прямоугольным параллелепипедом?
На доске открывается запись с пропусками:
Прямоугольный параллелепипед – это ______________________ фигура, ограниченная __________________________.
На доске открывается эталон:
«Прямоугольный параллелепипед – это пространственная фигура, ограниченная прямоугольниками».
– Далее исследование фигуры продолжим в паре. Выполните задание на карточках.
Найдите на моделях элементы параллелепипеда, посчитайте и запишите их количество:
граней – ________
вершин – ________
ребер – ________
2) Измерьте длину всех ребер. Запишите все измерения:___________________________________________________________
Сколько различных измерений у вас получилось? Запиши:___________________
При проверке дети на моделях показывают элементы фигуры, все понятия уточняются.
– А куб является параллелепипедом? В чем его особенности? (Куб – это особый параллелепипед, у него равны все ребра и грани; грани являются квадратами.)
– Пригодятся ли нам построенные формулы периметра и площади прямоугольника и квадрата для решения задач о параллелепипедах? В каком случае? (Да, если надо найти площадь его граней, длину ребер.)
– Итак, что вы повторили? (Понятие формулы, формулы площади и периметра прямоугольника и их единицы измерения, рассмотрели прямоугольный параллелепипед.)
– Для чего вы это повторили? (Чтобы открыть новое знание.)
4) Задание для пробного действия.
– Что вы будете делать дальше? (Будем выполнять задание на пробное действие.)
– Какая величина характеризует параллелепипед в силу того, то это пространственная фигура? (Объем.)
– В математике принято обозначать объем латинской буквой «V».
На доске появляется карточка с буквой
– Найдите объем вашего параллелепипеда.
Учащиеся работают с моделью параллелепипеда с измерениями 10 см, 8 см, 9 см, изготовленной дома.
– Что в этом задании для вас ново? (Надо найти объем фигуры.)
– Попробуйте выполнить задание на индивидуальной доске.
– Кто не смог найти объем параллелепипеда? В чем ваше затруднение? (Не нашли объем).
– Кто смог найти ответ?
Выписать на доску все варианты ответов детей.
Не исключена вероятность того, что учащиеся решат задачу верно, поэтому далее предложены два варианта ответов детей: первый, если есть разные варианты ответов, второй – если все решили одинаково.
– Что же получилось? (Мнения разделились. Все решили одинаково.)
– Как (с помощью какого эталона) доказать, кто прав (что вы правы)? (Такого эталона нет.)
– Чего же вы не смогли сделать? (Мы не смогли найти объем параллелепипеда. Мы не можем доказать, что решили задачу верно.)
3. Выявление места и причины затруднения.
Цель:
1) создать условия для проведения учащимися пошагового анализа своих действий с опорой на эталоны;
2) организовать выявление учащимися места и причины затруднения.
Организация учебного процесса на этапе 3:
– Вы выяснили, что у вас есть затруднение, значит… (Надо остановиться и подумать.)
– Какое задание вы выполняли? (Решали задачу на нахождение объема параллелепипеда.)
– В чем отличие этого задания от предыдущего? (Надо найти новую величину – объем.)
– Что не получилось? (Применить известные правила для решения данной задачи.)
– Почему же возникло затруднение? (У нас нет нужного способа для нахождения объема параллелепипеда.)
4. Построение проекта выхода из затруднения.
Цель:
1) сформулировать цель учебной деятельности;
2) согласовать тему урока;
3) выбрать способ и средства для построения нового знания.
Организация учебного процесса на этапе 4:
– Какова же цель вашей дальнейшей работы? (Открыть способ для нахождения объема параллелепипеда.)
– В виде чего может быть записан новый способ? (В виде формулы.)
– Что же вы должны сделать? (Вывести формулу для нахождения объема прямоугольного параллелепипеда.)
– Исходя из данной цели, уточните тему урока. (Формула объема прямоугольного параллелепипеда.)
На доску вывесить тему урока: Формула объема прямоугольного параллелепипеда.
– Составим план действий.
– Какие данные необходимы для формулы? (Измерения.)
– Где вы будете находить измерения параллелепипеда? (На модели параллелепипеда.)
– Что вам поможет установить связь между измерениями? (Арифметические действия.)
-К какому результату вы должны прийти? (Вывести формулу объема прямоугольного параллелепипеда.)
Учитель на доске фиксирует план действий.
1) Определить по модели параллелепипеда измерения.
2) Выбрать арифметическое действие.
3) Записать формулу для нахождения объёма прямоугольного параллелепипеда.
5. Реализация построенного проекта.
Цель:
1) создать условия для построения детьми нового способа для нахождения объема прямоугольного параллелепипеда.
2) применить новый способ действий для решения задачи, вызвавшей затруднение;
3) зафиксировать новый способ действия в речи и с помощью эталона;
4) зафиксировать преодоление возникшего затруднения;
5) выяснить, в каких единицах измеряется объем
.
Организация учебного процесса на этапе 5:
– По данному плану работаете в группах.
Разделить детей на группы по 4 – 5 человек, как это принято в классе.
– О чем надо помнить при работе в группах? (Учащиеся воспроизводят правила работы в группах.)
– Прочитайте задания на карточке. Есть ли вопросы? Приступайте к работе.
Ребята работают с одинаковой для всех моделью параллелепипеда.)
Карточка для работы в группах
Выложите кубики на дно данной модели.
Сосчитайте количество кубиков удобным способом.
Запишите решение: S = ____________
Запишите решение в общем виде: _S =____________
Дополните запись: «Площадь прямоугольника равна ______________________
(скольких?)________его измерений.»
Запиши единицы измерения площади прямоугольника: ____________________
Заполни кубиками весь объем параллелепипеда.
Сосчитай количество кубиков удобным способом.
З апиши решение: V =__________________
S
З апишите решение в общем виде: V =__________________ (записывают отдельно на листе бумаги)
S
Дополните запись: «Объем прямоугольного параллелепипеда равен _____________________ (скольких?) __________ его измерений.»
Запиши единицы измерения объема параллелепипеда: ____________________
(записывают отдельно на листе бумаги)
– Проверим работу (по заданиям карточки).
– Чему равно количество кубиков на дне модели? Как нашли?
Представитель одной группы сообщает ответ и решение. Остальные ребята показывают сигнальные карточки.
– Какую формулу вы применили для нахождения количества кубиков на дне модели? (Формулу площади прямоугольника: S = a · b)
– Как дополнили предложение? («Площадь прямоугольника равна произведению двух его измерений».)
– Какие единицы измерения площади прямоугольника написали? (мм2, см2, дм2, м2)
Проверка сигнальными карточками. Если есть ошибки – исправляем.
– Чему равно количество кубиков в параллелепипеде? Как нашли? (Проверка сигнальными карточками.)
– Какую формулу вы получили? (V = a · b · с)
– У кого такая же формула? (Дети показывают сигнальные карточки.)
– Как дополнили предложение? («Объем прямоугольного параллелепипеда равен произведению трех его измерений».)
– Кто не согласен? Почему? (Мнения детей.)
– Что разрешит ваши сомнения? (Учебник.)
– Обратитесь к выводам в учебнике на с. 89.
Дети читают вслух правило нахождения объема параллелепипеда.
– Совпал ли ваш вывод с выводом учебника? (Да, мы сделали правильный вывод.)
– Как найти объема параллелепипеда? (V = a · b · с)
Н а доске фиксируется формула
V = a · b · с
– Формулу объема можно читать разными способами.
Учащиеся по учебнику на с. 90 знакомятся с разными способами чтения формулы.
– Какие единицы измерения объема параллелепипеда написали? (мм3, см3, дм3, м3)
– Почему кубические единицы измерения? (Для нахождения объема используем 3 измерения: длину, ширину, высоту.)
– Найдите в учебнике предложение о единицах измерения объема и прочитайте его.
– Совпал ли ваш вывод с выводом учебника? (Да, мы сделали правильный вывод.)
На доске появляется эталон
Объем
Единицы измерения объема:
мм3, см3, дм3, м3
Если есть пособие «Построй свою математику», то учитель вывешивает эталон, а детям раздает соответствующий лист.
– Какой следующий шаг в работе? (Мы должны вернуться к пробному действию.)
– Можете справиться с решением задачи? (Да.)
– Что вам поможет? (Формула объема.)
– Пользуясь формулой, проверьте свое решение. (Дети работают индивидуально.)
– Проверьте по подробному образцу:
8 · 10 · 9 = 720 (см3)
Ответ:V равен 720 см3.
– У кого получился такой же ответ? (Дети показывают сигнальные карточки.)
Если есть неверные ответы, решение задачи разбирается.
– В чем вам помогает новый способ? (Находить объем параллелепипеда.)
6. Первичное закрепление с проговариванием во внешней речи.
Цель:
создать условия для выполнения учащимися типовых заданий на использование изученного способа действия с проговариванием во внешней речи.
Организация учебного процесса на этапе 6:
– Какова цель вашей дальнейшей деятельности? (Надо потренироваться в решении задач на новый способ.)
№ 4, стр. 90
– Откройте учебник на странице 90. Выполним задание № 4 под буквой а).
Один ученик объясняет решение задачи, работая у доски. Остальные дети записывают решение в тетрадях.
– Задачи под буквами б) и в) решите в парах, проговаривая формулу нахождения объема.
Обратите внимание на единицы измерения!
Одна пара работает на закрытой доске. Учитель в случае необходимости оказывает помощь этим ученикам. В результате получается подробный образец.
– Проверьте по образцу. (Дети показывают сигнальные карточки.)
Если есть ошибки, то их разобрать:
– В какой задаче допущена ошибка? В чем допущена ошибка?
– Что нужно знать, чтобы не допустить ошибок? (Формулу объема параллелепипеда, единицы измерения объема, быть внимательными при вычислениях.)
– Вы усвоили новый способ? Как это проверить? (Проверим себя, выполнив самостоятельную работу.)
7. Самостоятельная работа с самопроверкой по эталону.
Цель:
1) организовать самостоятельное выполнение учащимися типовых задач на применение нового способа действий;
2) организовать самопроверку учащимися своих решений по эталону для самопроверки;
3) создать (по возможности) ситуацию успеха для каждого ребёнка.
Организация учебного процесса на этапе 7:
– Выполните самостоятельно задание № 6 и ответьте только на первый вопрос.
– Проверьте свою работу по эталону для самопроверки.
Эталон для самопроверки с/р
3·4·7 = 84 (м3) V = a · b · с
– Оцените свою работу знаками «+» или «?»
– У кого есть ошибки? Где вы допустили ошибку?
Кто допустил ошибку, проговаривает решение по формуле или повторяет единицы измерения объема.
– Над чем вам надо поработать, чтобы не допускать ошибок? (…)
– Не расстраивайтесь, у вас все получиться.
-У кого ошибок нет? Хорошо. Мы все вместе двигаемся дальше.
8. Включение в систему знаний и повторение.
Цель:
научиться применять полученный новый способ действий в жизненных ситуациях
Организация учебного процесса на этапе 8:
– Где вы можете применить новое знание? (В решении любых задач, где нужно найти объем.)
– Сравните объемы аквариумов и поставьте соответствующий знак. (Дети работают в тетрадях, а знак выносят на индивидуальные доски.)
Рисунок на доске.
– Какой поставили знак? (Дети показывают знак на экранах.)
Учитель записывает все варианты ответов.
Учащиеся проверяют решения по эталону.
Эталон.
1)50·40·30 = 60 000 (см3)-V1
2)40·40 · 40 = 64 000 (см3)-V2
V1<V2
– Какие ошибки допустили? (На знание формулы, вычисления, постановка знака.)
– Какая формула помогла правильно найти объем каждого аквариума? ( Формула нахождения объема.)
9. Рефлексия учебной деятельности на уроке.
Цель:
1) организовать самооценку учениками собственной учебной деятельности на уроке;
2) соотнести цель и результаты своей учебной деятельности и зафиксировать степень их соответствия;
3) зафиксировать в речи новый способ действия, изученный на уроке;
4) зафиксировать затруднения, которые остались, и способы их преодоления;
5) обсудить и записать домашнее задание.
Организация учебного процесса на этапе 9:
– Какую цель вы перед собой ставили? (…)
– Достигли цели? Докажите. (Мы открыли формулу объема параллелепипеда.)
– Вспомним формулу. (Дети проговаривают еще раз V = a · b · с)
– Научились ли использовать новый способ?
– Кто сегодня учился? Как вы можете доказать? (Мы не умели, попробовали – не получилось, построили план проекта, работали по плану и сами открыли новый способ.)
– Все ли вам удалось в вашем путешествии? Оцените свою деятельность на уроке.
Дети оценивают свою деятельность на отрезке, ставят точку в том месте, где, по их мнению, они сейчас находятся.
– Какие трудности еще остались?
Домашнее задание:
стр. 90, № 1 (устно проговорить родителям), № 5 (в тетради)
– Где можно потренироваться? (Дома.)
Спасибо за работу на уроке!
Демонстрационный материал:
1) карточки с темой:
Формула объема прямоугольного параллелепипеда.
2) изображение фигур
3) модель параллелепипеда и куба (индивидуальные)
9 см
10 см
8 см
4) модель параллелепипеда и кубики (для групповой работы)
(а + в ) ·с = а ·с + в ·с
а· в · с = а ·(в· с)
5) эталоны для свойств умножения:
6)эталоны формул:
|
S = a · b |
Р = (а + в) ·2; Р = а · 2 + в · 2) |
7)эталоны единиц измерения:
|
Площадь Единицы измерения площади: мм2, см2, дм2, м2 |
Периметр Единицы измерения периметра: мм, см, дм, м |
Объем
Единицы измерения объема:
мм3, см3, дм3, м3
8) карточки со словами:
|
Пространственная |
Прямоугольники |
9) карточка с определением прямоугольного параллелепипеда:
«Прямоугольный параллелепипед – это пространственная фигура, ограниченная прямоугольниками».
10) карточки с буквами и числами:
360 – А; 100 – И; 40 – Ф; 112 – Г; 190 – Р; 120 – У
11) подробный образец выполнения пробного задания:
8 · 10 · 9 = 720 (см3)
Ответ:V равен 720 см3.
12) эталон для самопроверки самостоятельной работы:
Эталон для самопроверки с/р
3·4·7 = 84 ( м3 ) V=a · b · с
13) рисунки для решения задач:
14) эталон для проверки задачи на этапе «Включение в систему знаний и повторения»:
Эталон.
1)50·40·30 = 60 000 ( см3)-V1
2)40·40 · 40 = 64 000 ( см3)-V2
V1<V2
14
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/77475-formula-obema-prjamougolnogo-parallelepipeda













