Уже известны единицы измерения длины, например:
— и другие.
Для фигур на плоскости измеряют площадь в соответствующих квадратных единицах измерения:
мм2,см2,дм2,м2,км2…
Для геометрических тел измеряют объём, и для этого необходимы единицы измерения.
Единицей измерения объёма служит объём куба, у которого все грани равны (1) единице измерения длины:

мм3,см3,дм3,м3,км3…
Это кубический миллиметр, кубический сантиметр, кубический дециметр, кубический метр или даже кубический километр:
1км3=1000000000м3;1м3=1000дм3=1000000см3;1дм3=1000см3;1см3=1000мм3.
Часто для измерения объёма жидкости используют единицу измерения (1) литр:
1 л =1000см3=1дм3
.
Если измерять объём прямоугольного параллелепипеда, то можно представить, как маленькие кубики перекрывают прямоугольник в основании прямоугольного параллелепипеда.
Длины сторон прямоугольника определяют, сколько кубиков в ряду и сколько рядов с кубиками будет.
|
|
|
Если стороны равны, например, (3) см и (4) см, то прямоугольник перекрывается (3·4 = 12) кубиками.
Высота параллелепипеда определяет, сколько таких слоёв с кубиками можно поставить.
 |
|
Если высота прямоугольного параллелепипеда равна (3) см, то всего получится (3) слоя с кубиками. Итак, всего (3·3·4 = 36) кубиков, или объём равен (36) см³.
Значит, три измерения прямоугольного параллелепипеда позволяют посчитать, сколько всего кубиков поместилось в геометрическом теле, то есть вычислить объём прямоугольного параллелепипеда.
Пусть измерения прямоугольного параллелепипеда будут a, b и c единиц измерения.
Тогда объём (V = a·b·c) кубических единиц измерения.
Объем прямоугольного параллелепипеда


4.7
Средняя оценка: 4.7
Всего получено оценок: 509.
4.7
Средняя оценка: 4.7
Всего получено оценок: 509.
В школьном курсе математики за 5 класс, ученики знакомятся с темой прямоугольного параллелепипеда. Это одна из первых фигур курса, имеющих объем. Именно об объеме и формуле его нахождения пойдет речь сегодня.

Опыт работы учителем математики – более 33 лет.
Определения
Прямоугольным параллелепипедом называется фигура, все грани которого – прямоугольники. Фигура имеет шесть граней. Грани, пресекаясь, образовывают ребра, их 12.
Прямоугольный параллелепипед имеет четыре боковые грани и две грани оснований. В жизни мы часто сталкиваемся с данной фигурой: шкаф, холодильник, коробка – все они имеют форму прямоугольного параллелепипеда.
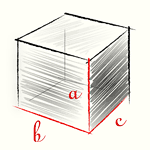
Формула объема данной фигуры
Объем куба (фигуры, все грани которого квадраты) со стороной 1 единица называется 1 кубическая единица.

Если заложить такими кубиками дно фигуры (рис. 3), то в длину понадобится 4 куба, а в ширину 3.
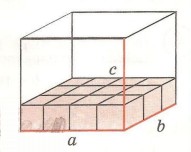
Таким образом, для заполнения основания необходимо:
3 х 4 =12 – так мы вычисляли площадь.
Чтобы заполнить всю фигуру и узнать объем, необходимо посчитать, сколько поместится в высоту таких слоев кубов, к примеру, если это будет 2, то объем составит:
3 х 4 х 2 = 24 кубов
Так, если учесть что длина основания фигуры 4 единицы, ширина – 3, высота – 2, то для того чтобы вычесть объем прямоугольного параллелепипеда необходимо найти произведение этих величин или измерений. Фигура, которая имеет три измерения, называется трехмерной либо объемной.
Для обозначения объема используют букву V.
Формула объема прямоугольного параллелепипеда имеет вид:
$$V = a · b · c$$
При необходимости все данные в задании необходимо перевести в одни единицы измерения.
Единицами измерения являются $мм^3, см^3, дм^3$ и так далее. Важно правильно читать: $1 м^3$ или кубический метр и так далее.
Английский иллюзионист провел 44 дня в стеклянном прямоугольном параллелепипеде, который был подвешен над рекой Темза. В его распоряжении была только вода, подушка, матрас и письменные принадлежности.
Задание: Вычислить объем фигуры, ширина которой 4 дм, длина 50 мм, а высота 10 см.
Решение: Для начала необходимо перевести все данные в одни единицы измерения.
$4 дм. = 40 см$;
$50 мм. = 5 см$.
$V = a • b • h$
$V = 40 • 5 • 10 = 200 см^3$
Таким образом, объем фигуры $V = 200 см^3$
Для измерения объема жидкости используют особую единицу измерения – литр (1 л).
Древние измерения жидкости, например кор = 220 л, бат = 22 л.
Измерения объема:
$$1 л = 1 000 см^3 = 1 дм^3$$
$$1 км^3 = 1000 000 000 м^3$$
$$1 м^3 = 1 000 дм^3 = 1 000 000 см^3$$
$$1 дм^3 = 1 000 см^3$$
$$1 см^3 = 1 000 мм^3$$

Что мы узнали?
Мы узнали, что для того, чтобы найти объем прямоугольного параллелепипеда необходимо умножить произведение длины и ширины основания на высоту фигуры. А также мы познакомились с единицами измерения объема.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Каролина Юсупова
5/5
-

Розочка Ангелиночка
5/5
-

Семён Сапьянов
4/5
-

Ярослава Ковалко
5/5
-

Армине Оганджанян
5/5
-

Егор Плисовский
4/5
-

Анастасия Прибыток
5/5
-

Lol Kek
5/5
-

Кирилл Лазарев
5/5
-

Илья Юрченко
5/5
Оценка статьи
4.7
Средняя оценка: 4.7
Всего получено оценок: 509.
А какая ваша оценка?

{V= a cdot b cdot c}
Найти объем параллелепипеда довольно просто. Для этого необходимо знать длины трех его сторон или же две стороны (площадь основания) и высоту. Чтобы облегчить расчет объема параллелепипеда мы создали калькулятор для разных исходных данных. Просто введите известные значения и в режиме онлайн получите результат.
Параллелепипед — многогранник, состоящий из шести граней, причем все они являются параллелограммами.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.
Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
Содержание:
- калькулятор объема параллелепипеда
- формула объема прямоугольного параллелепипеда через три стороны
- формула объема прямоугольного параллелепипеда через площадь основания и высоту
- формула объема наклонного параллелепипеда через длины сторон основания и высоту
- формула объема наклонного параллелепипеда через площадь основания и высоту
- примеры задач
Формула объема прямоугольного параллелепипеда через три стороны
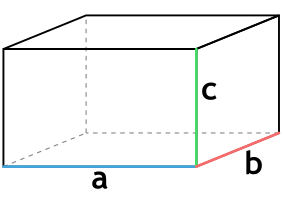
{V= a cdot b cdot c}
a – длина параллелепипеда
b – ширина параллелепипеда
c – высота параллелепипеда
Так как в основании параллелепипеда лежит прямоугольник, то в данной формуле ab – это площадь прямоугольника, который лежит в основании параллелепипеда. И тогда формулу можно сократить до {V= S h}
Формула объема прямоугольного параллелепипеда через площадь основания и высоту
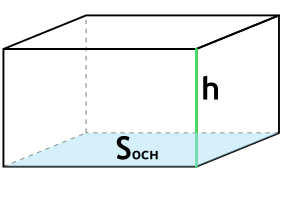
{V= S_{осн} cdot h}
Sосн – площадь основания параллелепипеда
h – высота параллелепипеда
Формула объема наклонного параллелепипеда через длины сторон основания и высоту
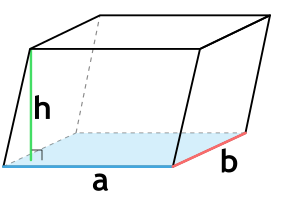
{V= a cdot b cdot h}
a – длина основания параллелепипеда
b – ширина основания параллелепипеда
h – высота параллелепипеда
Формула объема наклонного параллелепипеда через площадь основания и высоту
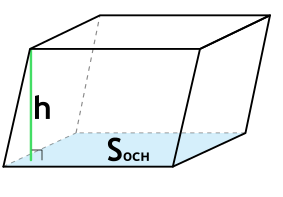
{V= S_{осн} cdot h}
Sосн – площадь основания параллелепипеда
h – высота параллелепипеда
Примеры задач на нахождение объема параллелепипеда
Задача 1
Найдите объём прямоугольного параллелепипеда с измерениями 3см, 4см и 5см.
Решение
Для решения данной задачи нам подходит формула один. Подставим в нее значения длины, ширины и высоты прямоугольного параллелепипеда, произведем расчет и получим ответ.
V= a cdot b cdot c = 3 cdot 4 cdot 5 = 60 : см^3
Ответ: 60 см³
Проверим правильность ответа с помощью калькулятора .
Задача 2
Найдите объём наклонного параллелепипеда с площадью основания 12м² и высотой 3м.
Решение
Используем для решения четвертую формулу. Подставим в нее площадь основания и высоту.
V= S_{осн} cdot h = 12 cdot 3 = 36 : м^3
Ответ: 36 м³
Полученный ответ поможет проверить калькулятор .
Сегодня Бим, Бом и ребята изучают объем геометрических фигур, геометрическую фигуру — прямоугольный параллелепипед, а также как найти объем прямоугольного параллелепипеда, и какие существуют единицы измерения объема.
Содержание статьи:
Объем геометрических фигур
Определение. Объем — это сколько места занимает фигура в пространстве.
Сегодня в цирке выходной. Бом прогуливает своих питомцев в парке, Бим помогает Бому.
— Вот я перед прогулкой зашел в магазин “Товары для животных” и купил специальные конфеты для твоих обезьянок, — обрадовал друга Бим. — Посмотри в какой объемной упаковке конфеты! Здесь можно измерить и длину, и ширину, и высоту коробки. А ведь раньше мы измеряли только длину и ширину донышка коробки.
— А ну-ка дай посмотреть! — попросил Бом. — Какая интересная коробка! Смотри, ее можно раскрыть с разных сторон.
— Ну да, — ответил Бим. — Ты только осторожнее, старайся открыть так, чтобы конфеты можно было вынуть только сверху. А то вдруг они разлетятся по всему парку! Попробуй тогда найди их все, да еще ведь и непонятно, сколько их там!
— Да, раньше мы рассматривали только плоские фигуры, — задумался Бом. — А у этой коробки могут быть три разных донышка, смотря с какой стороны ее открывать. И что же тогда в ней донышком называть? И как считать, сколько конфет в нее может поместиться? Вот если у донышка есть длина и ширина, но коробочка еще и высокая, то получается, что у нее и высота есть?
— Смотри, вон гуляют Коля, Вася и Оля! Может они нам объяснят?
Ребята тоже увидали Бима и Бома, да еще и с обезьянками. Как тут не подойти! Все радостно поздоровались друг с другом.
— Ой, какие обезьянки! — закричали дети.
Оля достала из сумочки банан:
— Можно угостить обезьянок? — спросила девочка.
— Конечно можно, — ответил Бом.
— Ой, у тебя, Оля, сумочка похожа на вот эту коробочку, у нее есть донышко, но она высокая. Значит, у сумочки тоже есть длина, ширина и высота. — удивился Бим. — Как же такие фигуры называются?
— Такие фигуры называются объемными, — ответил Вася. — Мы видим предметы вокруг нас: деревья, людей, машины, сумки, животных и еще очень много других предметов и у всех у них есть длина, ширина и высота.
— Люди договорились между собой, что такие предметы называются объемными, — добавил Коля, — и ввели понятие объема, то есть, сколько места занимает фигура в пространстве. Также решили, как измерять объем, — и ввели единицы измерения объема.
Объем прямоугольного параллелепипеда
Прямоугольный параллелепипед
Определение. Прямоугольный параллелепипед — это геометрическая фигура, имеющая внизу и вверху два одинаковых прямоугольника, у которых соответствующие вершины соединены отрезками, перпендикулярными к сторонам этих прямоугольников.
Объяснение продолжила Оля:
— Проще всего вычислить объем прямоугольного параллелепипеда. Прямоугольный параллелепипед — это геометрическая фигура, у которой внизу и вверху два одинаковых прямоугольника, соответствующие вершины прямоугольников соединяются отрезками. Эти отрезки перпендикулярны сторонам прямоугольников в верхнем и нижнем основаниях. Таких точек 8: 4 снизу и 4 сверху. В каждой такой точке получается 3 прямых угла и 3 отрезка.
Вот, посмотрите: на коробке тоже всего таких точек 8, из них 4 снизу на донышке и 4 сверху на крышечке. Эти 8 точек называют вершинами параллелепипеда. 12 линий (4 вверху, 4 внизу и 4 по бокам), которые соединяют вершины параллелепипеда называют ребрами, ребра образуют 6 прямоугольников (2 основания — донышко и крышечка, и 4 боковые стороны), которые называются гранями параллелепипеда.
Находим объем прямоугольного параллелепипеда
Правило. Для вычисления объема прямоугольного параллелепипеда надо длину основания умножить на ширину основания и умножить на высоту параллелепипеда.
Дальше объяснял Вася:
— Для того чтобы вычислить объем прямоугольного параллелепипеда, надо измерить длину двух прилегающих сторон прямоугольников (a, b) в основании и измерить длину ребра соединяющего нижнее и верхнее основания — это высота параллелепипеда (h). И потом перемножить длину этих сторон.
V = a × b × h (куб. ед. дл.).
— Давайте измерим объем вашей коробки и объем Олиной сумки, — предложил Коля.
Мальчик достал из портфеля угольник и начал прикладывать его по очереди к каждому углу коробки:
— Видно, что все углы прямые, — сделал вывод Коля. — Значит у нас прямоугольный параллелепипед. Длина и ширина сторон основания 5 см и 4 см:
a = 5 см, b = 4 см.
Высота параллелепипеда, то есть, длина отрезка, соединяющего верхнее и нижнее основания, — равна 6 см:
h = 6 см.
Значит, объем параллелепипеда равен
V = a × b × h, V = 5 × 4 × 6 = 120 (куб. см).
— Теперь измерим объем моей сумки-портфеля, — продолжила Оля. — Смотрим: все углы прямые, значит — можем воспользоваться формулой для объема прямоугольного параллелепипеда. Здесь у нас:
длина 30 см = 3 дм, ширина 20 см = 2 дм, высота 40 см = 4 дм.
Объем равен
V = 3 × 2 × 4 = 24 куб. дм.
Единицы измерения объема.
Единицами измерения объема являются:
1 куб. мм, 1 куб. см, 1 куб. дм, 1 куб. м, 1 куб. км,1 л.
— А в каких еще единицах измеряют объем? — поинтересовался Бим.
— Кроме кубических сантиметров и кубических дециметров, объем измеряют еще в кубических метрах, кубических миллиметрах, кубических километрах и в литрах, — ответил Вася. — Один литр равен объему куба (прямоугольный параллелепипед, у которого все стороны одинаковые) со стороной в 1 дм.
1 л = 1 куб. дм.
Кстати, Оля! Получается, что объем твоей сумки равен 24 л.
— При вычислении объема все три измерения — длина, ширина и высота, — должны быть записаны в одинаковых единицах измерения длины: или в миллиметрах, или в сантиметрах, или в дециметрах, или в метрах, или в километрах, — заметил Коля. Затем применяют формулу вычисления объема прямоугольного параллелепипеда:
V = a × b × h (куб. ед. дл.).
Если надо, то числа раздробляют, а уже после вычисления объем укрупняют. Есть специальные таблицы для перевода одних единиц измерения объема в другие единицы измерения объема.
Таблицы перевода единиц измерения объема
1 куб. см = 1000 куб. мм
1 куб. дм = 1000 куб. см
1 куб. дм = 1000 000 куб. мм
1 куб. дм = 1л
1 куб. м = 1000 000 000 куб. мм
1 куб. м = 1000 000 куб. см
1 куб. м = 1000 куб. дм
1 куб. м = 1000 л
1 куб. км = 1018 куб. мм
1 куб. км = 1015 куб. см
1 куб. км = 1012 куб. дм
1 куб. км = 109 куб. м
— Давайте теперь запишем для ребят вопросы, — подытожил Бом:
- Что такое объем?
- Что такое прямоугольный параллелепипед?
- Как найти объем прямоугольного параллелепипеда?
- Единицы измерения объема — это?
И ответы:
- Объем — это количество места, которое занимает фигура в пространстве.
- Прямоугольный параллелепипед — это геометрическая фигура, имеющая внизу и вверху два одинаковых прямоугольника, у которых соответствующие вершины соединены отрезками, перпендикулярными к сторонам этих прямоугольников.
- Для вычисления объема прямоугольного параллелепипеда надо длину основания умножить на ширину основания и умножить на высоту параллелепипеда.
- Единицы измерения объема — это:
1 куб. мм, 1 куб.см, 1 куб.дм, 1 куб. м , 1 куб.км,1 л.
Заключение
— Бим, пойдем отведем обезьянок в цирк, — поглядел на часы Бом. — Им пора обедать. Спасибо, ребята! Вы нам с Бимом помогли разобраться, что такое объем, что такое прямоугольный параллелепипед, найти объем прямоугольного параллелепипеда, узнать единицы измерения объема. До встречи в цирке!
Оригинальная идея подачи материала принадлежит Стуловой Лилии Валериевне (преподаватель математики от 5 лет и старше).
Не забудьте оценить наши старания! Комментарии приветствуются!)))
Математика
5 класс
Урок №32
Объём прямоугольного параллелепипеда. Единицы объёма
Перечень рассматриваемых вопросов:
– куб;
– параллелепипед;
– элементы параллелепипеда;
– объём прямоугольного параллелепипеда, куба.
Тезаурус
Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками.
Высота, длина и ширина – это измерения прямоугольного параллелепипеда.
Единичный куб – куб, ребро которого равно линейной единице.
Обязательная литература
1. Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О.Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Как вы думаете, что больше занимает места– 1 кг ваты или 1 кг гвоздей? Чтобы ответить на этот вопрос, нужно знать величину, которая называется объём. В данной задаче ответ очевиден, так как мы можем представить предметы визуально. Но не всегда ответ может быть таким простым. Чаще всего нужно произвести определённые вычисления.
Сегодня мы рассмотрим объём прямоугольного параллелепипеда и научимся его находить.
Объём можно измерить. Его измеряют в кубических миллиметрах, кубических сантиметрах, кубических метрах, литрах и т. д.
Найдём соотношение между единицами измерения объёма.
Так как 1 см = 10 дм, то 1 см3 = 1 000 мм3.
1 дм3 = 1000 см3 = 1 л
1 м3 = 1000 дм3
1 км3 = 1000000000 м3
В древности в разных частях планеты люди по-разному измеряли объём. Например, в Древней Греции использовали глиняные мерные сосуды для зерна или жидкостей. Причём это были амфоры разного размера. Поэтому значение единицы объёма менялось от 2 до 26 литров.
На Руси основной мерой жидкостей считалось ведро, в котором 10 кружек или 12 литров. Также для подсчётов объём ведра делили пополам, то есть на два полуведра, которые, в свою очередь, тоже можно было поделить пополам. Для торговли с иностранцами использовали меру объёма, называемую бочка, которая равнялась 40 вёдрам.
Дадим определение единичного куба – это куб, ребро которого равно линейной единице. Его тоже принимают за единицу объёма.
Если прямоугольный параллелепипед можно разрезать на К единичных кубов, то говорят, что его объём V равен К кубическим единицам.
Например, на рисунке объём параллелепипеда равен 24 кубическим единицам.

V = 24 куб. единиц
Введём формулу объёма прямоугольного параллелепипеда.
Объём прямоугольного параллелепипеда равен произведению трёх его измерений, то есть произведению длины а, ширины bи высоты c, или произведению площади основания S на высоту c.
V = а · b · c = S · с
Так как куб является прямоугольным параллелепипедом, у которого все измерения равны, то его объём равен третьей степени длины его ребра а.
V = а3
Решим задачу.
Мальчик купил аквариум в форме прямоугольного параллелепипеда, который имеет площадь дна, равную 1400 см3, и высоту 6 дм. Какой объём воды он налил в аквариум, если уровень жидкости не доходил до края 5 см? Выразите ответ в кубических сантиметрах.
Чтобы решить эту задачу переведём единицы измерения длины в сантиметры.
6 дм = 60 см
Получается, что высота аквариума равна 60 см. Но по условию задачи требуется определить объём налитой жидкости, а её высота соответствует разности между высотой аквариума и уровнем жидкости, не доходящей до края:
с = 60 см – 5 см = 55 см
Получается, что высота жидкости в сосуде соответствует 55 см.
Теперь можно определить объём воды, которая налита в аквариум.
Для этого используем следующую формулу:
V = S · с = 1400 см2 · 55 см = 77000 см3
Ответ: мальчик налил в аквариум 77000 см3 воды.
Разбор решения заданий тренировочного модуля
№ 1. Чему равен объём куба, если длина его ребра равна 3 см?
Решение: для нахождения объёма куба нужно воспользоваться формулой.
V = а3 = (3 см)3 = 27 см3
Ответ: 27 см3.
№2. Как изменится объём прямоугольного параллелепипеда, если его длину увеличить в три раза. Подчеркните правильный ответ.
Решение: чтобы ответить на вопрос, нужно воспользоваться формулой для вычисления объёма прямоугольного параллелепипеда.
V = а · b · c, где а – длина прямоугольного параллелепипеда.
Если длина возрастет в три раза, то объём, соответственно, увеличится в три раза, так как, длина – это один из трёх множителей, входящих в формулу объёма прямоугольного параллелепипеда:
V = 3 · а · b · c
Ответ: объём увеличится в три раза.



