
{V= a cdot b cdot c}
Найти объем параллелепипеда довольно просто. Для этого необходимо знать длины трех его сторон или же две стороны (площадь основания) и высоту. Чтобы облегчить расчет объема параллелепипеда мы создали калькулятор для разных исходных данных. Просто введите известные значения и в режиме онлайн получите результат.
Параллелепипед — многогранник, состоящий из шести граней, причем все они являются параллелограммами.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.
Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
Содержание:
- калькулятор объема параллелепипеда
- формула объема прямоугольного параллелепипеда через три стороны
- формула объема прямоугольного параллелепипеда через площадь основания и высоту
- формула объема наклонного параллелепипеда через длины сторон основания и высоту
- формула объема наклонного параллелепипеда через площадь основания и высоту
- примеры задач
Формула объема прямоугольного параллелепипеда через три стороны
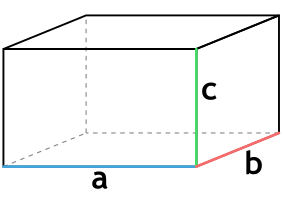
{V= a cdot b cdot c}
a – длина параллелепипеда
b – ширина параллелепипеда
c – высота параллелепипеда
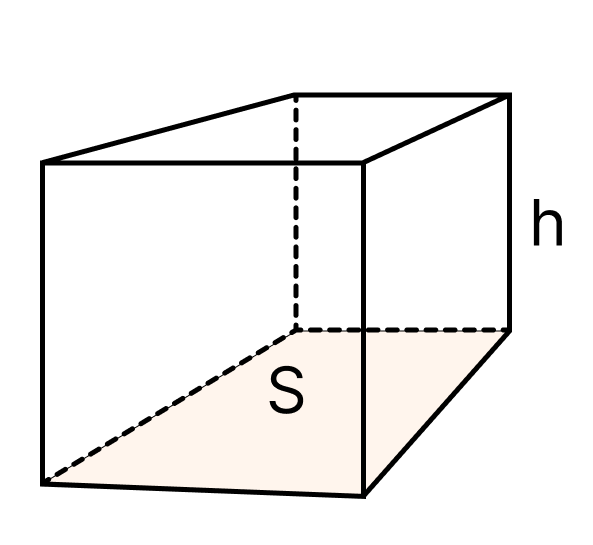
Так как в основании параллелепипеда лежит прямоугольник, то в данной формуле ab – это площадь прямоугольника, который лежит в основании параллелепипеда. И тогда формулу можно сократить до {V= S h}
Формула объема прямоугольного параллелепипеда через площадь основания и высоту
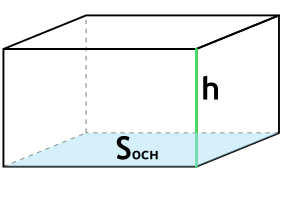
{V= S_{осн} cdot h}
Sосн – площадь основания параллелепипеда
h – высота параллелепипеда
Формула объема наклонного параллелепипеда через длины сторон основания и высоту
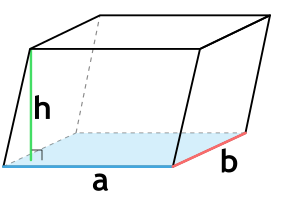
{V= a cdot b cdot h}
a – длина основания параллелепипеда
b – ширина основания параллелепипеда
h – высота параллелепипеда
Формула объема наклонного параллелепипеда через площадь основания и высоту
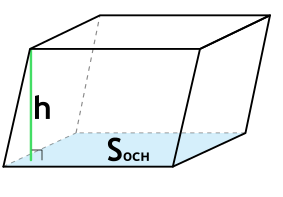
{V= S_{осн} cdot h}
Sосн – площадь основания параллелепипеда
h – высота параллелепипеда
Примеры задач на нахождение объема параллелепипеда
Задача 1
Найдите объём прямоугольного параллелепипеда с измерениями 3см, 4см и 5см.
Решение
Для решения данной задачи нам подходит формула один. Подставим в нее значения длины, ширины и высоты прямоугольного параллелепипеда, произведем расчет и получим ответ.
V= a cdot b cdot c = 3 cdot 4 cdot 5 = 60 : см^3
Ответ: 60 см³
Проверим правильность ответа с помощью калькулятора .
Задача 2
Найдите объём наклонного параллелепипеда с площадью основания 12м² и высотой 3м.
Решение
Используем для решения четвертую формулу. Подставим в нее площадь основания и высоту.
V= S_{осн} cdot h = 12 cdot 3 = 36 : м^3
Ответ: 36 м³
Полученный ответ поможет проверить калькулятор .
В данной публикации мы рассмотрим, как можно найти объем параллелепипеда и разберем примеры решения задач для закрепления материала.
-
Формула вычисления объема параллелепипеда
- 1. Общая формула
- 2. Объем прямоугольного параллелепипеда
- Примеры задач
Формула вычисления объема параллелепипеда
1. Общая формула
Объем любого параллелепипеда равняется произведению площади его основания на высоту.
V = Sосн ⋅ h

- Sосн – площадь основания (ABCD или EFHG, равны между собой);
- h – высота.
Данная формула справедлива для всех видов геометрической фигуры:
- наклонной – боковые грани не перпендикулярны основаниям;
- прямой – все боковые грани (4 шт.) являются прямоугольниками;
- прямоугольной – все грани (боковые и основания) являются прямоугольниками;
- ромбоэдра – все грани являются равными ромбами;
- куба – все грани представляют собой равные квадраты.
2. Объем прямоугольного параллелепипеда
Объем фигуры равен произведению его длины на ширину на высоту.
V = a ⋅ b ⋅ c

Формула следует из следующих утверждений:
- Основанием фигуры является прямоугольник, площадь которого считается как произведение его длины (a) на ширину (b).
- Высота фигуры – это длина боковой грани (c).
Примеры задач
Задание 1
Найдите объем параллелепипеда, если известно, что площадь его основания равняется 20 см2, а высота – 7 см.
Решение:
Используем первую формулу, подставив в нее известные нам значения:
V = 20 см2 ⋅ 7 см = 140 см3.
Задание 2
Дан прямоугольный параллелепипед. Длина и ширина его основания равны 9 см и 5 см, соответственно, а высота составляет 6 см. Найдите объем фигуры.
Решение:
Воспользуемся формулой для данного типа фигуры:
V = 9 см ⋅ 5 см ⋅ 6 см = 270 см3.
Найти объем параллелепипеда через площадь основания
где: S — площадь основания, h — высота
Параллелепипед — это многогранник, каждая из граней которого являются параллелограммами
Формула расчета объема параллелепипеда через площадь основания и высоту:
V = Sh
Через ширину, длину, высоту
Через площадь основания
Найти
Параллелепипед
Расчет объема
Пирамида
Конус
Цилиндр
Призма
Куб
Шар
Как найти объем параллелепипеда через основание
Под параллелепипедом имеется ввиду объемная геометрическая фигура, многогранник, основанием и боковыми гранями которого являются параллелограммы. Основание параллелепипеда – это тот четырехугольник, на котором этот многогранник визуально “лежит”. Найти объем параллелепипеда через его основание очень легко.
Инструкция
Как было сказано выше, основанием параллелепипеда является параллелограмм. Для того, чтобы найти объем параллелепипеда, необходимо выяснить площадь того параллелограмма, который лежит в основании. Для это, в зависимости от известных данных, существуют несколько формул:
S = a*h, где а – сторона параллелограмма, h – высота, проведенная к этой стороне;м
S = a*b*sinα, где, a и b – стороны параллелограмма, α – угол между данными сторонами.
Пример 1: Дан параллелограмм, у которого одна из сторон равна 15 см, длина высоты, проведенной к данной стороне, 10 см. Тогда, чтобы найти площадь данной фигуры на плоскости, применяется первая из двух указанных выше формул:
S = 10*15 = 150 см²
Ответ: Площадь параллелограмма составляет 150 см²
Теперь, разобравшись с тем, как находить площадь параллелограмма, можно приступить к нахождению объема параллелепипеда. Объем параллелепипеда можно найти по формуле:
V = S*h, где h – высота данного параллелепипеда, S – площадь его основания, нахождение которой было рассмотрено выше.
Можно рассмотреть пример, который бы включал решенную выше задачу:
Площадь основания параллелограмма 150 см², его высота, допустим, 40 см, требуется найти объем данного параллелепипеда. Решается эта задача при помощи данной выше формулы:
V = 150*40 = 6000 см³
Одной из разновидностей параллелепипеда является прямоугольный параллелепипед, у которого боковые грани и основание являются прямоугольниками. У этой фигуры найти объем еще проще, чем у обычного прямого параллелепипеда, нахождение объема которого было рассмотрено выше:
V = a*b*c, где a, b, c, – это длина, ширина и высота данного параллелепипеда.
Пример: У прямоугольного параллелепипеда длина и ширина основания составляют 12 см и 14 см, длина боковой грани (высоты) 14 см, требуется вычислить объем фигуры. Решается задача таким вот образом:
V = 12*14*14 = 2352 см³
Ответ: объем прямоугольного параллелепипеда равен 2352 см³
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Прямой параллелепипед [править | править вики-текст]
Площадь боковой поверхности Sб=Ро*h, где Ро — периметр основания, h — высота
Площадь полной поверхности Sп=Sб+2Sо, где Sо — площадь основания
Объём V=Sо*h
Прямоугольный параллелепипед [править | править вики-текст]
Основная статья: Прямоугольный параллелепипед
Площадь боковой поверхности Sб=2c(a+b), где a, b — стороны основания, c — боковое ребро прямоугольного параллелепипеда
Площадь полной поверхности Sп=2(ab+bc+ac)
Объём V=abc, где a, b, c — измерения прямоугольного параллелепипеда.
Куб [править | править вики-текст]
Площадь поверхности: S=6a^2
Объём: V=a^3, где a — ребро куба.
Произвольный параллелепипед [править | править вики-текст]
Объём и соотношения в наклонном параллелепипеде часто определяются с помощью векторной алгебры. Объём параллелепипеда равен абсолютной величине смешанного произведения трёх векторов, определяемых тремя сторонами параллелепипеда, исходящими из одной вершины. Соотношение между длинами сторон параллелепипеда и углами между ними даёт утверждение, что определитель Грама указанных трёх векторов равен квадрату их смешанного произведения [2]:215.
В математическом анализе [править | править вики-текст]
В математическом анализе под n-мерным прямоугольным параллелепипедом B понимают множество точек x = (x_1,ldots,x_n) вида B = {x|a_1leqslant x_1leqslant b_1,ldots,a_nleqslant x_nleqslant b_n}
