Калькулятор объема параллелепипеда
Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
Что известно
Размерность
Длина
см
Ширина
см
Площадь основания
см2
Высота
см
Раcсчитать
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие страницы
- 📢 Поделиться и комментировать
🧑🏾💻 Что считает калькулятор
Калькулятор объема параллелепипеда – это инструмент, который позволяет вычислять объем любого параллелепипеда и выводить результат в разных единицах измерения.
📦 Как использовать калькулятор
Укажите значение сторон для прямоугольного параллелепипеда или сторон и высоты для наклонного, после этого калькулятор произведет расчёт и выдаст его в указанных единицах измерения.
📐 Что влияет на точность расчетов калькулятора
Точность расчетов калькулятора объема параллелепипеда зависит от нескольких факторов:
- Корректность ввода данных. Если вводимые значения длины, ширины и высоты параллелепипеда некорректны, то расчет объема будет неправильным. Поэтому, важно убедиться в правильности вводимых значений перед выполнением расчета.
- Точность математических операций. Расчет объема параллелепипеда требует выполнения математических операций, таких как умножение. Если калькулятор не выполняет математические операции точно, то результаты расчетов будут неточными.
- Точность округления. в некоторых случаях, результаты расчетов могут быть округлены. Если калькулятор округляет результаты до неправильного числа знаков, то результаты будут неточными.
- Алгоритм расчета. Различные калькуляторы могут использовать разные алгоритмы расчета. Если алгоритм расчета неправильный, то результаты могут быть неточными.
- Ошибки программирования. Если в программе калькулятора есть ошибки, то результаты расчетов могут быть неправильными. Поэтому, важно использовать калькуляторы, которые были разработаны и протестированы надежными разработчиками.
🗂️ Где можно применить калькулятор
Калькулятор объема параллелепипеда может быть использован во многих областях, где требуется расчет объема параллелепипеда. Некоторые из таких областей включают:
- Строительство. Калькулятор объема параллелепипеда может использоваться строителями при расчете объема блоков в форме параллелепипеда, бетонных блоков, кирпичей и других материалов, используемых в строительстве.
- Производство. Калькулятор объема параллелепипеда может использоваться в производственных процессах для расчета объема материалов, таких как металл, пластик, стекло и другие, используемых в производстве изделий.
- Логистика. Калькулятор объема параллелепипеда может использоваться при планировании грузоперевозок, чтобы определить, сколько грузовых мест может вместить транспортное средство.
- Образование. Калькулятор объема параллелепипеда может использоваться учителями математики в школах и университетах для обучения геометрии и расчета объема.
- Интерьер и дизайн. Калькулятор объема параллелепипеда может использоваться в дизайне интерьера для расчета объема элементов в форме параллелепипеда, таких как шкафы, полки, столы и другие.
- Ремонт и обслуживание. Калькулятор объема параллелепипеда может использоваться в ремонте и обслуживании, чтобы определить количество материалов, необходимых для замены элементов, таких как плитка, обои и другие.
🤔 Как вычислить объем параллелепипеда самостоятельно
Объем параллелепипеда можно вычислить самостоятельно, используя формулу:
V = a * b * h
где a, b, и h – это соответственно длины трех сторон параллелепипеда.
Шаги для вычисления объема параллелепипеда:
- Измерьте длину одной из сторон параллелепипеда и запишите ее значение. Обозначим ее как “a”.
- Измерьте длину второй стороны и запишите ее значение. Обозначим ее как “b”.
- Измерьте высоту параллелепипеда и запишите ее значение. Обозначим ее как “h”.
- Умножьте значение “a” на значение “b”.
- Умножьте результат из шага 4 на значение “h”.
- Полученный результат будет объемом параллелепипеда.
Например, если длина первой стороны равна 3 см, длина второй стороны равна 4 см, а высота равна 5 см, то объем параллелепипеда будет:
V = 3 см * 4 см * 5 см = 60 куб. см
🤓 Полезные советы
Несколько советов, которые могут помочь при вычислении объема параллелепипеда:
- Определите тип параллелепипеда: правильный, прямоугольный или наклонный. Это позволит выбрать правильную формулу для расчета объема.
- Измерьте длину, ширину и высоту параллелепипеда в соответствующих единицах измерения. Обычно используются метры, сантиметры или дюймы.
- Убедитесь, что все измерения были взяты в одной системе измерения. Если это не так, преобразуйте измерения в одну систему измерения.
- Примените правильную формулу для расчета объема, в зависимости от типа параллелепипеда. Для правильного параллелепипеда объем равен длине ребра в кубе. Для прямоугольного параллелепипеда объем равен произведению длины, ширины и высоты. Для наклонного параллелепипеда объем равен площади основания, умноженной на высоту.
- Проверьте свои вычисления, чтобы избежать ошибок. Дважды проверьте формулу и убедитесь, что все измерения были взяты правильно.
- Используйте калькулятор или компьютерную программу для автоматического расчета объема. Это может сократить время и снизить вероятность ошибок.
- Округляйте результат до нужного количества знаков после запятой, в зависимости от требований задачи.
❓ Вопросы и ответы
А вот несколько ответов на часто задаваемые вопросы про вычисление объема параллелепипеда.
Что такое параллелепипед и как он выглядит?
Параллелепипед – это геометрическое тело, имеющее шесть прямоугольных граней. Он выглядит как прямоугольный блок с равными гранями и прямыми углами между ними.
Как рассчитать объем параллелепипеда?
Объем параллелепипеда можно вычислить, умножив длину, ширину и высоту параллелепипеда. Формула для расчета объема V = l * w * h, где V – объем, l – длина, w – ширина и h – высота параллелепипеда.
Как измерить длину, ширину и высоту параллелепипеда?
Для измерения длины, ширины и высоты параллелепипеда необходимо использовать линейку или мерную ленту. Длину измеряют вдоль одной из его граней, ширину – вдоль другой грани, а высоту – перпендикулярно этим граням.
Как связаны площадь основания и высота с объемом параллелепипеда?
Объем параллелепипеда зависит от площади его основания и высоты. Чем больше площадь основания и высота параллелепипеда, тем больше будет его объем.
В каких единицах измеряется объем параллелепипеда?
Объем параллелепипеда измеряется в кубических единицах длины, таких как кубические метры, кубические сантиметры, кубические дюймы и т. д.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
- Калькулятор площади трапеции. Рассчитайте онлайн площадь трапеции, не только зная длины ее оснований и высоту, но и по другим известным параметрам, например, диагоналям.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
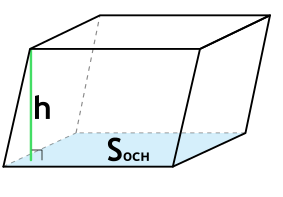
Как найти объем параллелепипеда
На данной странице калькулятор поможет рассчитать объем параллелепипеда онлайн. Для расчета задайте высоту, ширину и длину. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Через стороны
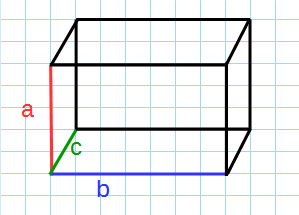
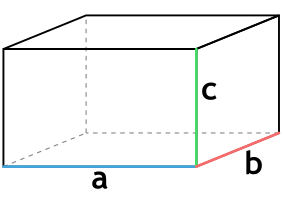
Формула объема параллелепипеда через его ребра:
a,b,c – ребра параллелепипеда.
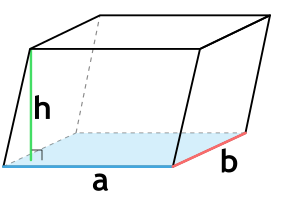
Через стороны и высоту
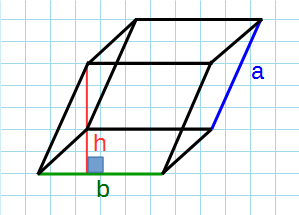
Формула объема параллелепипеда:
a,b – ребра параллелепипеда; h – высота параллелепипеда.

{V= a cdot b cdot c}
Найти объем параллелепипеда довольно просто. Для этого необходимо знать длины трех его сторон или же две стороны (площадь основания) и высоту. Чтобы облегчить расчет объема параллелепипеда мы создали калькулятор для разных исходных данных. Просто введите известные значения и в режиме онлайн получите результат.
Параллелепипед — многогранник, состоящий из шести граней, причем все они являются параллелограммами.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.
Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
Содержание:
- калькулятор объема параллелепипеда
- формула объема прямоугольного параллелепипеда через три стороны
- формула объема прямоугольного параллелепипеда через площадь основания и высоту
- формула объема наклонного параллелепипеда через длины сторон основания и высоту
- формула объема наклонного параллелепипеда через площадь основания и высоту
- примеры задач
Формула объема прямоугольного параллелепипеда через три стороны
{V= a cdot b cdot c}
a – длина параллелепипеда
b – ширина параллелепипеда
c – высота параллелепипеда
Так как в основании параллелепипеда лежит прямоугольник, то в данной формуле ab – это площадь прямоугольника, который лежит в основании параллелепипеда. И тогда формулу можно сократить до {V= S h}
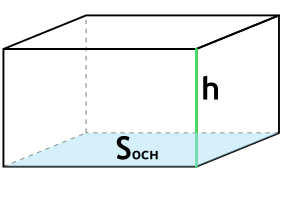
Формула объема прямоугольного параллелепипеда через площадь основания и высоту
{V= S_{осн} cdot h}
Sосн – площадь основания параллелепипеда
h – высота параллелепипеда
Формула объема наклонного параллелепипеда через длины сторон основания и высоту
{V= a cdot b cdot h}
a – длина основания параллелепипеда
b – ширина основания параллелепипеда
h – высота параллелепипеда
Формула объема наклонного параллелепипеда через площадь основания и высоту
{V= S_{осн} cdot h}
Sосн – площадь основания параллелепипеда
h – высота параллелепипеда
Примеры задач на нахождение объема параллелепипеда
Задача 1
Найдите объём прямоугольного параллелепипеда с измерениями 3см, 4см и 5см.
Решение
Для решения данной задачи нам подходит формула один. Подставим в нее значения длины, ширины и высоты прямоугольного параллелепипеда, произведем расчет и получим ответ.
V= a cdot b cdot c = 3 cdot 4 cdot 5 = 60 : см^3
Ответ: 60 см³
Проверим правильность ответа с помощью калькулятора .
Задача 2
Найдите объём наклонного параллелепипеда с площадью основания 12м² и высотой 3м.
Решение
Используем для решения четвертую формулу. Подставим в нее площадь основания и высоту.
V= S_{осн} cdot h = 12 cdot 3 = 36 : м^3
Ответ: 36 м³
Полученный ответ поможет проверить калькулятор .
Сегодня Бим, Бом и ребята изучают объем геометрических фигур, геометрическую фигуру — прямоугольный параллелепипед, а также как найти объем прямоугольного параллелепипеда, и какие существуют единицы измерения объема.
Содержание статьи:
Объем геометрических фигур
Определение. Объем — это сколько места занимает фигура в пространстве.
Сегодня в цирке выходной. Бом прогуливает своих питомцев в парке, Бим помогает Бому.
— Вот я перед прогулкой зашел в магазин “Товары для животных” и купил специальные конфеты для твоих обезьянок, — обрадовал друга Бим. — Посмотри в какой объемной упаковке конфеты! Здесь можно измерить и длину, и ширину, и высоту коробки. А ведь раньше мы измеряли только длину и ширину донышка коробки.
— А ну-ка дай посмотреть! — попросил Бом. — Какая интересная коробка! Смотри, ее можно раскрыть с разных сторон.
— Ну да, — ответил Бим. — Ты только осторожнее, старайся открыть так, чтобы конфеты можно было вынуть только сверху. А то вдруг они разлетятся по всему парку! Попробуй тогда найди их все, да еще ведь и непонятно, сколько их там!
— Да, раньше мы рассматривали только плоские фигуры, — задумался Бом. — А у этой коробки могут быть три разных донышка, смотря с какой стороны ее открывать. И что же тогда в ней донышком называть? И как считать, сколько конфет в нее может поместиться? Вот если у донышка есть длина и ширина, но коробочка еще и высокая, то получается, что у нее и высота есть?
— Смотри, вон гуляют Коля, Вася и Оля! Может они нам объяснят?
Ребята тоже увидали Бима и Бома, да еще и с обезьянками. Как тут не подойти! Все радостно поздоровались друг с другом.
— Ой, какие обезьянки! — закричали дети.
Оля достала из сумочки банан:
— Можно угостить обезьянок? — спросила девочка.
— Конечно можно, — ответил Бом.
— Ой, у тебя, Оля, сумочка похожа на вот эту коробочку, у нее есть донышко, но она высокая. Значит, у сумочки тоже есть длина, ширина и высота. — удивился Бим. — Как же такие фигуры называются?
— Такие фигуры называются объемными, — ответил Вася. — Мы видим предметы вокруг нас: деревья, людей, машины, сумки, животных и еще очень много других предметов и у всех у них есть длина, ширина и высота.
— Люди договорились между собой, что такие предметы называются объемными, — добавил Коля, — и ввели понятие объема, то есть, сколько места занимает фигура в пространстве. Также решили, как измерять объем, — и ввели единицы измерения объема.
Объем прямоугольного параллелепипеда
Прямоугольный параллелепипед
Определение. Прямоугольный параллелепипед — это геометрическая фигура, имеющая внизу и вверху два одинаковых прямоугольника, у которых соответствующие вершины соединены отрезками, перпендикулярными к сторонам этих прямоугольников.
Объяснение продолжила Оля:
— Проще всего вычислить объем прямоугольного параллелепипеда. Прямоугольный параллелепипед — это геометрическая фигура, у которой внизу и вверху два одинаковых прямоугольника, соответствующие вершины прямоугольников соединяются отрезками. Эти отрезки перпендикулярны сторонам прямоугольников в верхнем и нижнем основаниях. Таких точек 8: 4 снизу и 4 сверху. В каждой такой точке получается 3 прямых угла и 3 отрезка.
Вот, посмотрите: на коробке тоже всего таких точек 8, из них 4 снизу на донышке и 4 сверху на крышечке. Эти 8 точек называют вершинами параллелепипеда. 12 линий (4 вверху, 4 внизу и 4 по бокам), которые соединяют вершины параллелепипеда называют ребрами, ребра образуют 6 прямоугольников (2 основания — донышко и крышечка, и 4 боковые стороны), которые называются гранями параллелепипеда.
Находим объем прямоугольного параллелепипеда
Правило. Для вычисления объема прямоугольного параллелепипеда надо длину основания умножить на ширину основания и умножить на высоту параллелепипеда.
Дальше объяснял Вася:
— Для того чтобы вычислить объем прямоугольного параллелепипеда, надо измерить длину двух прилегающих сторон прямоугольников (a, b) в основании и измерить длину ребра соединяющего нижнее и верхнее основания — это высота параллелепипеда (h). И потом перемножить длину этих сторон.
V = a × b × h (куб. ед. дл.).
— Давайте измерим объем вашей коробки и объем Олиной сумки, — предложил Коля.
Мальчик достал из портфеля угольник и начал прикладывать его по очереди к каждому углу коробки:
— Видно, что все углы прямые, — сделал вывод Коля. — Значит у нас прямоугольный параллелепипед. Длина и ширина сторон основания 5 см и 4 см:
a = 5 см, b = 4 см.
Высота параллелепипеда, то есть, длина отрезка, соединяющего верхнее и нижнее основания, — равна 6 см:
h = 6 см.
Значит, объем параллелепипеда равен
V = a × b × h, V = 5 × 4 × 6 = 120 (куб. см).
— Теперь измерим объем моей сумки-портфеля, — продолжила Оля. — Смотрим: все углы прямые, значит — можем воспользоваться формулой для объема прямоугольного параллелепипеда. Здесь у нас:
длина 30 см = 3 дм, ширина 20 см = 2 дм, высота 40 см = 4 дм.
Объем равен
V = 3 × 2 × 4 = 24 куб. дм.
Единицы измерения объема.
Единицами измерения объема являются:
1 куб. мм, 1 куб. см, 1 куб. дм, 1 куб. м, 1 куб. км,1 л.
— А в каких еще единицах измеряют объем? — поинтересовался Бим.
— Кроме кубических сантиметров и кубических дециметров, объем измеряют еще в кубических метрах, кубических миллиметрах, кубических километрах и в литрах, — ответил Вася. — Один литр равен объему куба (прямоугольный параллелепипед, у которого все стороны одинаковые) со стороной в 1 дм.
1 л = 1 куб. дм.
Кстати, Оля! Получается, что объем твоей сумки равен 24 л.
— При вычислении объема все три измерения — длина, ширина и высота, — должны быть записаны в одинаковых единицах измерения длины: или в миллиметрах, или в сантиметрах, или в дециметрах, или в метрах, или в километрах, — заметил Коля. Затем применяют формулу вычисления объема прямоугольного параллелепипеда:
V = a × b × h (куб. ед. дл.).
Если надо, то числа раздробляют, а уже после вычисления объем укрупняют. Есть специальные таблицы для перевода одних единиц измерения объема в другие единицы измерения объема.
Таблицы перевода единиц измерения объема
1 куб. см = 1000 куб. мм
1 куб. дм = 1000 куб. см
1 куб. дм = 1000 000 куб. мм
1 куб. дм = 1л
1 куб. м = 1000 000 000 куб. мм
1 куб. м = 1000 000 куб. см
1 куб. м = 1000 куб. дм
1 куб. м = 1000 л
1 куб. км = 1018 куб. мм
1 куб. км = 1015 куб. см
1 куб. км = 1012 куб. дм
1 куб. км = 109 куб. м
— Давайте теперь запишем для ребят вопросы, — подытожил Бом:
- Что такое объем?
- Что такое прямоугольный параллелепипед?
- Как найти объем прямоугольного параллелепипеда?
- Единицы измерения объема — это?
И ответы:
- Объем — это количество места, которое занимает фигура в пространстве.
- Прямоугольный параллелепипед — это геометрическая фигура, имеющая внизу и вверху два одинаковых прямоугольника, у которых соответствующие вершины соединены отрезками, перпендикулярными к сторонам этих прямоугольников.
- Для вычисления объема прямоугольного параллелепипеда надо длину основания умножить на ширину основания и умножить на высоту параллелепипеда.
- Единицы измерения объема — это:
1 куб. мм, 1 куб.см, 1 куб.дм, 1 куб. м , 1 куб.км,1 л.
Заключение
— Бим, пойдем отведем обезьянок в цирк, — поглядел на часы Бом. — Им пора обедать. Спасибо, ребята! Вы нам с Бимом помогли разобраться, что такое объем, что такое прямоугольный параллелепипед, найти объем прямоугольного параллелепипеда, узнать единицы измерения объема. До встречи в цирке!
Оригинальная идея подачи материала принадлежит Стуловой Лилии Валериевне (преподаватель математики от 5 лет и старше).
Не забудьте оценить наши старания! Комментарии приветствуются!)))
Калькулятор для расчета объема параллелепипеда
C помощью нашего Онлайн-калькулятора для расчета объема параллелепипеда Вы можете быстро и точно рассчитать объем прямоугольного параллелепипеда. Для того, чтобы вычислить объем прямоугольного параллелепипеда, введите значение ребер “a”, “b”, “c” и нажмите кнопку “Рассчитать”. Также Вы можете указать точность полученного результата, т.е. количество знаков после запятой, до которого будет округлен рассчитанный объем параллелепипеда.
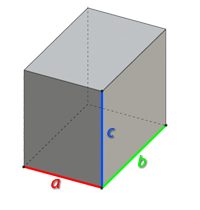
Задайте значение ребер параллелепипеда а, b, c и нажмите кнопку “Рассчитать”
Округлить результат до
знаков после запятой
Рассчитать
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Объем прямоугольного параллелепипеда вычисляется по следующей формуле:
,
где a, b, c – ребра параллелепипеда.