Задание 8. ЕГЭ. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 7
Рубрика Задание 8, Решаем ЕГЭ по математике Комментарии (0)
Задание. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 7. Найдите объем параллелепипеда.
Решение:
Объем прямоугольного параллелепипеда равен: V = a·b·c
Так как прямоугольный параллелепипед описан около цилиндра, то
a = b = 2R = 2·7 = 14
c = h = 7
V = 14·14·7 = 1372
Ответ: 1372
Понравилось? Нажмите
Оставить комментарий
Рубрики
- Демоверсия ЕГЭ по информатике
- Демоверсия ЕГЭ по математике
- Демоверсия ОГЭ по информатике
- Демоверсия ОГЭ по математике
- Материалы по аттестации
- Решаем ЕГЭ по математике
- Задание 1
- Задание 10
- Задание 11
- Задание 12
- Задание 13
- Задание 14
- Задание 15
- Задание 16
- Задание 2
- Задание 3
- Задание 4
- Задание 5
- Задание 6
- Задание 7
- Задание 8
- Задание 9
- Решаем ОГЭ по математике
- Задание 21
- Задание 22
- Задание 24
- Скачать экзаменационные варианты по информатике
- ЕГЭ по информатике
- ОГЭ по информатике
- Скачать экзаменационные варианты по математике
- ЕГЭ по математике
- ОГЭ по математике
- Тематическое планирование
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Шар вписан в цилиндр. Площадь полной поверхности цилиндра равна 18. Найдите площадь поверхности шара.
2
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
3
Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра.
4
В куб вписан шар радиуса 1. Найдите объем куба.
5
В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны
Найдите объем цилиндра, описанного около этой призмы.
Пройти тестирование по этим заданиям
Задание
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
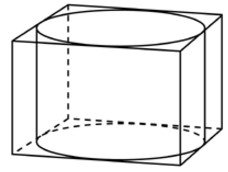
Решение
- Объем прямоугольного параллелепипеда равен произведению его высоты на площадь основания. А площадь основания равна произведению длины на ширину: V=h*Socн=h*a · b.
- Высота параллелепипеда равна высоте цилиндра, то есть 1. Длина и ширина основания параллелепипеда равны диаметру цилиндра (диаметр равен двум радиусам), то есть 2.
- V = 1*2*2 = 4 – объем прямоугольного параллелепипеда.
Ответ: 4
Прямоугольный параллелепипед описан около…
Задание:
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.
Решение:
* Объем параллелепипеда = Sосн * h, где Sосн – площадь основания, h – высота параллелепипеда. Высота вписанного цилиндра равна высоте параллелепипеда. По условию задачи h = 1.
* Цилиндр вписан в параллелепипед и его радиус r = 1, значит сторона параллелепипеда равен a = 2r = 2 * 1 = 2.
* В основании параллелепипеда – квадрат, а значит Sосн = 2 * 2 = 4 (ед)2
* Объем параллелепипеда = Sосн * h = 4 * 1 = 4 (ед)3
Ответ: 4
Решение
Основанием параллелепипеда является прямоугольник, описанный около окружности радиусом 5. Значит, этот прямоугольник является квадратом, сторона которого равна диаметру окружности основания цилиндра. Так как радиус r этой окружности равен 5, то диаметр равен двум радиусам, то есть 10. Объём параллелепипеда V находим по формуле V = Sосн · h = (2cdot r)^2cdot r, где h — высота параллелепипеда, которая равна высоте цилиндра, то есть равна 5. Значит, объем параллелепипеда V=10^2cdot5=500.
Ответ
500
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.


