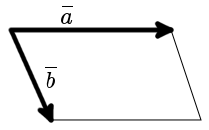
A parallelogram refers to a four-sided figure that has two sets of parallel and congruent sides. For example, a square is a parallelogram. However, not all parallelograms are squares because parallelograms do not have to have four 90 degree angles. Since parallelograms are two-dimensional shapes, you can find the area but not the volume. To find the area, you need to know the base length and height of the parallelogram.
Select one pair of sides of the parallelogram as the base sides. It doesn’t matter which pair of sides because both pairs of sides must be parallel and congruent.
Measure the distance between the two base sides to find the height of the parallelogram.
Measure the length of one of the base sides. It does not matter which side you measure because they are congruent so it will be the same length.
Multiply the base length times the height to find the area of the parallelogram. In this example, if the height equals 5 inches and the base equals 9 inches, multiply 5 by 9 to get an area of 45 square inches.
какая формула объема параллелограмма
Настя Настя
Ученик
(101),
закрыт
8 лет назад
Лучший ответ
Noname
Мастер
(1066)
8 лет назад
Если имел ввиду параллелепипед, то V=SH=abc
NonameМастер (1066)
8 лет назад
или имела
Остальные ответы
GWAR
Искусственный Интеллект
(244922)
8 лет назад
шхдхв
NonameМастер (1066)
8 лет назад
интеллект дал сбой
GWAR
Искусственный Интеллект
(244922)
у тебя?? ? объем тебе и написал ширина длина высота перемножить
Анатолий Крылов
Искусственный Интеллект
(134816)
8 лет назад
Это плоская фигура
Анна ГлинкинаОракул (63194)
8 лет назад
Самое похожее слово это параллелепипед)
Анна Глинкина
Оракул
(63194)
8 лет назад
У плоских фигур нет объема, так как у них двумерное пространство
Пётр ГордиенкоЗнаток (429)
5 лет назад
Строить умных не нужно тут. У нас даже в практической работе сказано найти объем параллелограмма!
Похожие вопросы
Как найти объем параллелепипеда через основание
Под параллелепипедом имеется ввиду объемная геометрическая фигура, многогранник, основанием и боковыми гранями которого являются параллелограммы. Основание параллелепипеда – это тот четырехугольник, на котором этот многогранник визуально “лежит”. Найти объем параллелепипеда через его основание очень легко.
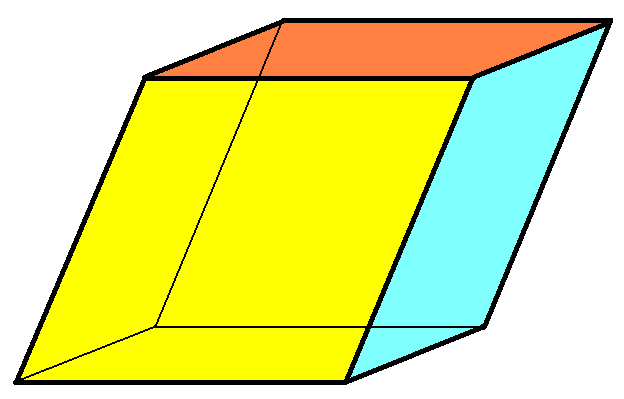
Инструкция
Как было сказано выше, основанием параллелепипеда является параллелограмм. Для того, чтобы найти объем параллелепипеда, необходимо выяснить площадь того параллелограмма, который лежит в основании. Для это, в зависимости от известных данных, существуют несколько формул:
S = a*h, где а – сторона параллелограмма, h – высота, проведенная к этой стороне;м
S = a*b*sinα, где, a и b – стороны параллелограмма, α – угол между данными сторонами.
Пример 1: Дан параллелограмм, у которого одна из сторон равна 15 см, длина высоты, проведенной к данной стороне, 10 см. Тогда, чтобы найти площадь данной фигуры на плоскости, применяется первая из двух указанных выше формул:
S = 10*15 = 150 см²
Ответ: Площадь параллелограмма составляет 150 см²
Теперь, разобравшись с тем, как находить площадь параллелограмма, можно приступить к нахождению объема параллелепипеда. Объем параллелепипеда можно найти по формуле:
V = S*h, где h – высота данного параллелепипеда, S – площадь его основания, нахождение которой было рассмотрено выше.
Можно рассмотреть пример, который бы включал решенную выше задачу:
Площадь основания параллелограмма 150 см², его высота, допустим, 40 см, требуется найти объем данного параллелепипеда. Решается эта задача при помощи данной выше формулы:
V = 150*40 = 6000 см³
Одной из разновидностей параллелепипеда является прямоугольный параллелепипед, у которого боковые грани и основание являются прямоугольниками. У этой фигуры найти объем еще проще, чем у обычного прямого параллелепипеда, нахождение объема которого было рассмотрено выше:
V = a*b*c, где a, b, c, – это длина, ширина и высота данного параллелепипеда.
Пример: У прямоугольного параллелепипеда длина и ширина основания составляют 12 см и 14 см, длина боковой грани (высоты) 14 см, требуется вычислить объем фигуры. Решается задача таким вот образом:
V = 12*14*14 = 2352 см³
Ответ: объем прямоугольного параллелепипеда равен 2352 см³
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Параллелограмм относится к четырехсторонней фигуре, которая имеет два набора параллельных и конгруэнтных сторон. Например, квадрат – это параллелограмм. Однако не все параллелограммы являются квадратами, потому что параллелограммы не должны иметь четыре угла 90 градусов. Поскольку параллелограммы представляют собой двумерные фигуры, вы можете найти область, но не объем. Чтобы найти область, вам нужно знать базовую длину и высоту параллелограмма.
Выберите одну пару сторон параллелограмма в качестве базовых сторон. Не имеет значения, какая пара сторон, потому что обе пары сторон должны быть параллельными и конгруэнтными.
Измерьте расстояние между двумя базовыми сторонами, чтобы найти высоту параллелограмма.
Измерьте длину одной из базовых сторон. Неважно, какую сторону вы измеряете, потому что они совпадают, поэтому она будет одинаковой длины.
Умножьте базовую длину на высоту, чтобы найти площадь параллелограмма. В этом примере, если высота равна 5 дюймам, а основание равно 9 дюймам, умножьте 5 на 9, чтобы получить площадь 45 квадратных дюймов.
Объем параллелепипеда, построенного на векторах онлайн
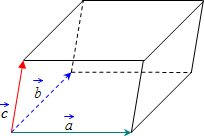
Объём параллелепипеда равен смешанному произведению векторов на которых он построен:
Поскольку смешанное произведение векторов, может быть отрицательным числом, а объём геометрического тела – всегда число положительное, то при вычислении объёма параллелепипеда, построенного на векторах, результат смешанного произведения берется по модулю:
Таким образом, для того, чтобы вычислить объём параллелепипеда, построенного на векторах, нужно найти смешанное произведение данных векторов, и полученный результат взять по модулю.
Наш онлайн калькулятор, найдет площадь параллелепипеда с описанием подробного хода решения на русском языке.
Как найти объем параллелограмма по векторам
№ 1
Найти объём параллелепипеда, построенного на векторах , , .
Решение
Объём параллелепипеда, построенного на векторах a, b, c численно равен модулю смешанного произведения этих векторов.
V = | abc |
V = | -7 | = 7
№ 2
Найти объём пирамиды, построенной на векторах , , .
Решение
Объём пирамиды, построенной на векторах a, b, c равен 1/6 объёма параллелепипеда, построенного на этих векторах.
Объём параллелепипеда, построенного на векторах a, b, c численно равен модулю смешанного произведения этих векторов.
V = | abc |/6
V = | -7 | /6= 7/6
№ 3
Найти объём тетраэдра ABCD.
Решение
Построим векторы AB, AC, AD.
, , .
Объём тетраэдра, построенного на векторах AB, AC, AD равен 1/6 объёма параллелепипеда, построенного на этих векторах.
Объём параллелепипеда, построенного на векторах AB, AC, AD численно равен модулю смешанного произведения этих векторов.
V = | AB · AC· AD |/6
V = | 12 | /6 = 12/6 = 2
Онлайн калькулятор. Площадь параллелограмма построенного на векторах.
Этот онлайн калькулятор позволит вам очень просто найти площадь параллелограмма построенного на векторах.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление площади параллелограмма построенного на векторах и закрепить пройденый материал.
Калькулятор для вычисления площади параллелограмма построенного на векторах
Выберите каким образом задается параллелограмм:
Введите значения векторов: Введите координаты трех любых вершин параллелограмма:
Инструкция использования калькулятора для вычисления площади параллелограмма построенного на векторах
Ввод данных в калькулятор для вычисления площади параллелограмма построенного на векторах
В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора вычисления площади параллелограмма построенного на векторах
- Между полями для ввода можно перемещаться нажимая клавиши “влево” и “вправо” на клавиатуре.
Теория. Площадь параллелограмма построенного на векторах.
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
[spoiler title=”источники:”]
http://ludmilav2.narod.ru/index/0-65
http://ru.onlinemschool.com/math/assistance/vector/parallelogram_area/
[/spoiler]