Онлайн решение Пирамиды по координатам вершин
Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольной пирамиды (тетраэдра):
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;
8) основания, площади и уравнения биссекторов;
9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Пирамида (др.-греч. πυραμίς, πυραμίδος) — многогранник, одна из граней которого (называемая основанием) — произвольный многоугольник, а остальные грани (называемые боковыми гранями) — треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные (тетраэдр), четырёхугольные и т. д. Пирамида является частным случаем конуса.
Лемма
Две пирамиды, имеющие равные высоты и равновеликие основания, имеют равные объемы.
Теорема
Объем пирамиды равен одной трети произведения площади основания на высоту: (V={1over3}S*H) , где S – площадь основания, H – высота пирамиды.
Теорема
Объем V усеченной пирамиды может быть найден по формуле (V={1over3}H(S1+{{sqrt {S1S2}}}+S2)), где H – высота усеченной пирамиды, S1 и S2 – площади ее оснований.
Часто даны координаты вершин пирамиды ABCD и требуется найти ее объем. Даная задача может быть решена методами аналитической геометрии. Покажем ее решение на примере.
Пусть даны координаты вершин пирамиды ABCD и требуется найти ее объем: A(10;6;6), B(-2;8;2), C(6;8;9), D(7;10;3).
Решение
Объем пирамиды равен (1over6) объема параллелепипеда, построенного на векторах AB, AC, AD. Найдем координаты этих векторов, для этого из соответствующей координаты конца вектора вычтем координату его начала:
AB=(-12;2;-4), AC=(-4;2:3), AD=(-3;4;-3).
Тогда объем параллелепипеда равен значению детерминанта (определителя) матрицы, составленной из координат векторов (строка матрицы – координаты вектора). Определитель третьего порядка находим по правилу треугольников.
Автор – Дмитрий Айстраханов
Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Расчет объема пирамиды
(по значениям координат 4-ех вершин)
На данной странице представлен онлайн калькулятор для расчета объема пирамиды по значениям
координат 4-ех вершин. Объем пирамиды Вы можете найти в режиме реального времени, просто введя свои данные!
На нашем сайте Вы найдете много программ для решения задач по геометрии.
См. также Вычисление объема пирамиды через площадь ее основания и высоту.
Введите координаты 4-ех вершин пирамиды:
| А: | ( | , | , | ) | Координаты точки А, 1-ой вершины. |
| В: | ( | , | , | ) | Координаты точки В, 2-ой вершины. |
| С: | ( | , | , | ) | Координаты точки С, 3-ей вершины. |
| D: | ( | , | , | ) | Координаты точки D, 4-ой вершины. |
Примеры нахождения объема пирамиды: Пример № 1,
Пример № 2
- Расчет объема шара
- Расчет объема куба
Если после использования данного онлайн калькулятора
(Расчет объема пирамиды) у Вас возникли какие-то вопросы по работе сервиса или вопросы
образовательного характера, то Вы всегда можете задать их на нашем
форуме.
Вы поняли, как решать? Нет?
Рассчитайте цену решения ваших задач


Калькулятор
стоимости
Решение контрольной
от 300 рублей
*
* Точная стоимость будет определена после загрузки задания для исполнителя
+Загрузить файл
Файлы doc, pdf, xls, jpg, png не более 5 МБ.

Аналитическая геометрия – задача на расчет пирамиды (тетраэдра)
Краткая теория
Вузовская аналитическая геометрия отличается от курса школьной геометрии. Главное отличие состоит в том, что она основным своим инструментом имеет набор алгебраических формул и методов вычислений. В основе аналитической геометрии лежит метод координат.
Аналитическая геометрия имеет набор формул, готовых уравнений и алгоритмов действия. Для успешного и правильного решения главное – разобраться и уделить задаче достаточно времени.
Данная задача является типовой в курсе аналитической геометрии и требует использования различных методов и знаний, таких как декартовые прямоугольные координаты и вектора в пространстве.
Пример решения задачи
Задача
Даны координаты
вершин пирамиды
. Найти:
Сделать чертеж.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Длина ребра
Длину ребра
найдем по
формуле расстояния между 2-мя точками:
Угол между ребрами
Угол между ребрами
и
найдем как угол
между направляющими векторами
и
:
Косинус угла между
векторами:
Угол между ребром и гранью. Векторное произведение
Вычислим угол между
ребром
и гранью
.
Для этого вычислим
координаты нормального вектора плоскости
–им будет
векторное произведение векторов
и
.
Найдем векторное произведение. Для этого
вычислим определитель:
Нормальный вектор
плоскости:
Синус угла:
Площадь грани
Вычислим площадь
грани
. Она будет численно равна половине модуля векторного
произведения векторов
и
:
Искомая площадь:
Объем пирамиды. Смешанное произведение векторов
Вычислим объем
пирамиды. Он будет равен шестой части модуля смешанного произведения векторов
и
:
Для того чтобы вычислить смешанное произведение, необходимо
найти определитель квадратной матрицы, составленной из координат векторов:
Искомый объем
пирамиды:
Уравнение прямой в пространстве
Вычислим уравнение
прямой
. Направляющим
вектором искомой прямой является вектор
. Кроме того, прямая проходит через точку
Уравнение искомой
прямой:
Уравнение плоскости
Вычислим уравнение
плоскости
. Нормальный вектор плоскости
. кроме того, плоскость проходит через точку
-уравнение
грани
Уравнение высоты, опущенной на грань
Составим уравнение
высоты, опущенной на грань
из вершины
:
Нормальный вектор
является
направляющим вектором высоты, кроме того, высота проходит через точку
Искомое уравнение
высоты:
Сделаем схематический чертеж:
Часто в задачах школьного курса геометрии приходится решать задания, которые требуют использования комплексного подхода. Одной из таких задач является вычисление объема пирамиды по координатам вершин. Как решить эту геометрическую задачу – ответит приведенная ниже статья.
Что представляет собой пирамида?
Говоря простыми словами, под этой фигурой понимают пространственный объект, ограниченный треугольными сторонами и одной многоугольной гранью, которая называется основанием. Многоугольное основание может быть произвольным n-угольником на плоскости, например, правильным треугольником, параллелограммом и так далее.
Любая пирамида имеет n + 1 грань, 2 * n ребер и n + 1 вершину. Вершины фигуры не являются равноправными. Так, существует единственная вершина, которая не принадлежит основанию. Она называется главной. Расстояние от нее до плоскости основания – это высота фигуры.
Пирамиды могут быть наклонными, если высота пересекает основание не в его центре, или прямыми, когда высота с основанием пересекается в геометрическом центре последнего. Также фигуры могут быть неправильными и правильными. Пирамиды правильные состоят из равноугольного и равностороннего основания и нескольких равнобедренных треугольников, которые друг другу равны.
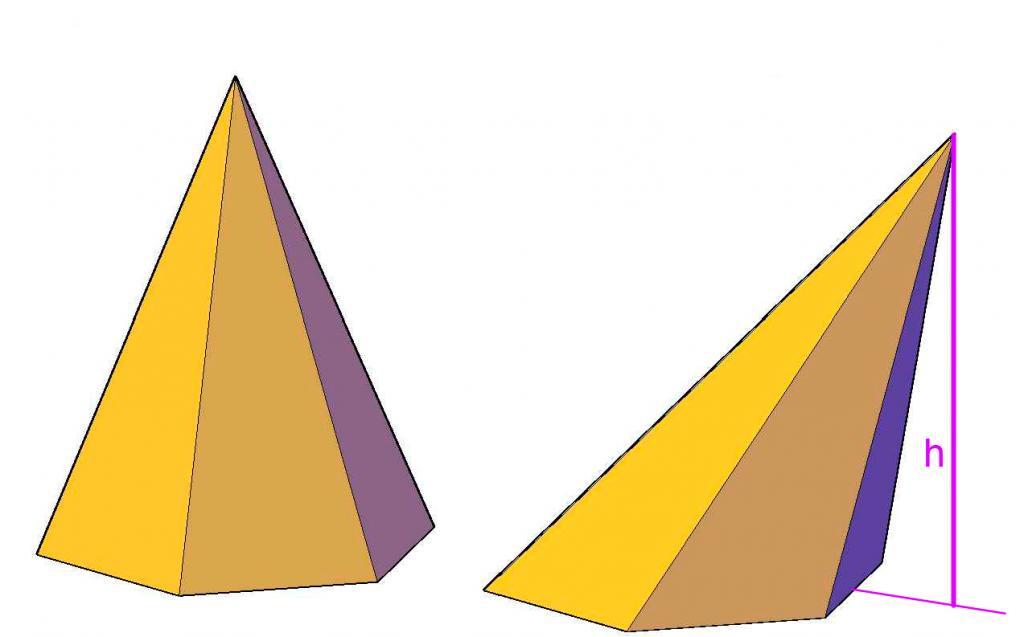
Как рассчитывается объем пирамиды?
Прежде чем приводить методику вычисления по координатам вершин объема пирамиды, следует привести формулу, при помощи которой можно рассчитать эту величину для фигуры любого типа из рассматриваемого класса. Итак, объем пирамиды рассчитывается так:
V = 1 / 3 * So * h.
Здесь So – это основания площадь, h – расстояние от главной вершины до основания, то есть высота пирамиды.
Таким образом, любая геометрическая задача на нахождение объема пирамиды сводится к расчету величин So и h.
Как найти объем пирамиды по координатам вершин: методика
Пирамида может быть представлена произвольным n-угольным основанием. Чтобы рассчитать его площадь, следует внимательно изучить условие задачи, в котором должно быть сказано, о каком типе n-угольника идет речь. Если это треугольник или параллелограмм, то расчет его площади по известным координатам очень прост: необходимо лишь найти векторное произведение соответствующих векторов сторон.
Вычислить высоту пирамиды также не представляет особого труда. Для этого следует из любых трех точек основания получить уравнение плоскости в общем виде, а затем нужно воспользоваться формулой расстояния между плоскостью и точкой (вершиной пирамиды). Формула имеет вид:
d = |(A * x1 + B * y1 + C * z1 + D)| / √(A2 + B2 + C2).
Здесь (x1; y1; z1) – координаты точки.
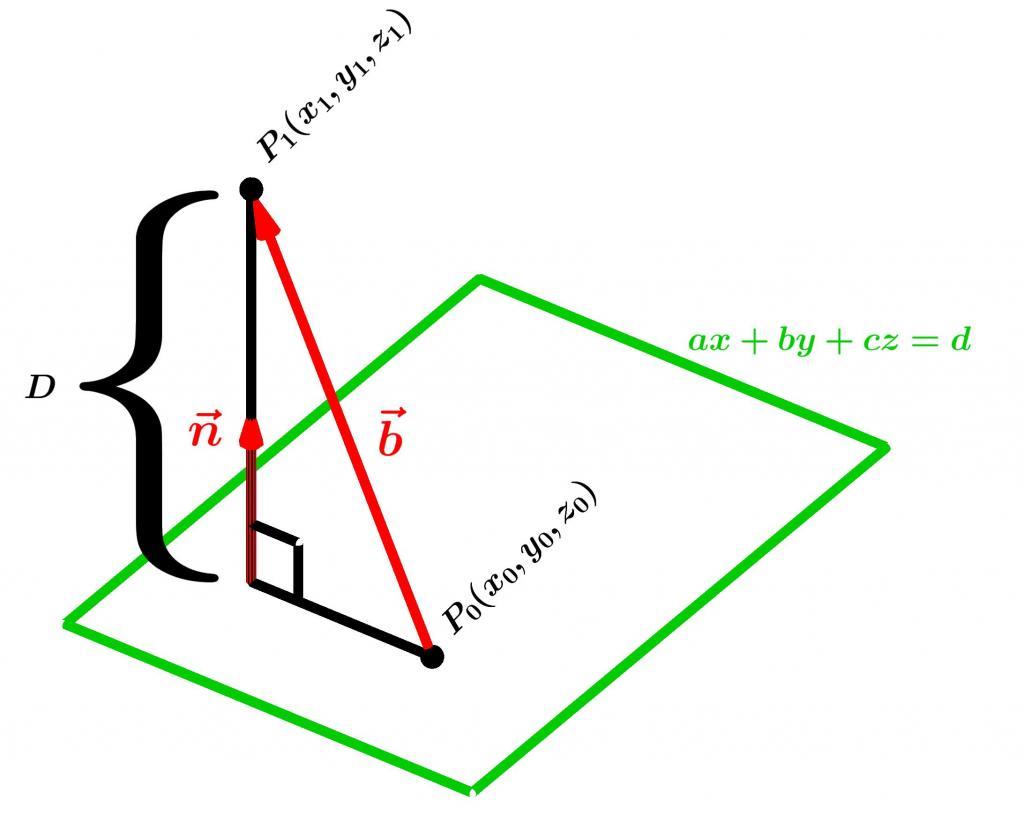
Уравнение плоскости имеет вид:
A * x + B * y + C * z + D = 0.
Задача с треугольной пирамидой

Решим задачу на примере самой простой пирамиды – треугольной. Условие простое: ниже даны координаты вершин пирамиды, объем найти нужно для фигуры, которая на этих координатах построена:
- A(1; 0; 3);
- B(0; 2; -1);
- C(3; 3; 1);
- D(4; 3; 4).
Положим, что основание пирамиды является треугольником ABC. Найдем длины векторов AB¯ и AC¯:
AB¯ = (-1; 2; -4);
AC¯ = (2; 3; -2).
Векторное произведение AB¯ и AC¯ даст нам, с одной стороны, двойную площадь треугольника, то есть 2 * So, а с другой стороны, мы получим координаты нормального к плоскости вектора n¯, имеем:
n¯ = [AB¯ * AC¯] = (8; -10; -7).
Площадь треугольного основания равна полудлине вектора n¯, то есть:
So = √(82 + 102 + 72) / 2 = 7,3.
Прежде чем рассчитывать расстояние от D до плоскости ABC, необходимо записать уравнение плоскости. Три его коэффициента (A, B, C) мы уже знаем, они соответствуют координатам нормали n¯. Свободный член можно получить, подставив в уравнение координаты любой точки плоскости, например точки A, имеем:
D = -1 * (A * x1 + B * y1 + C * z1) = -1 * (8 * 1 + (-10) * 0 + (-7) * 3) = 13.
Тогда уравнение плоскости основания пирамиды принимает форму:
8 * x – 10 * y – 7 * z + 13 = 0.
Теперь применяем приведенную выше формулу для расчета расстояния от точки D(4; 3; 4) до найденной плоскости, получаем:
d = |(8 * 4 – 10 * 3 – 7 * 4 + 13)| / √(82 + 102 + 72) = 0,89.
Поскольку найденное значение расстояния d соответствует высоте пирамиды треугольной h, то можно воспользоваться формулой для объема фигуры:
V = 1 / 3 * So * h = 1 / 3 * 7,3 * 0,89 ≈ 2,166.
Полученное значение объема выражено в кубических единицах выбранной координатной системы.


