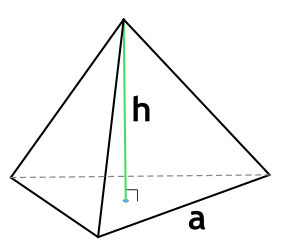
Пирамида – это многогранник, основанием которого является многоугольник, а грани его являются треугольниками.
Онлайн-калькулятор объема пирамиды
У пирамиды есть ребра. Можно сказать, что они тянутся к точке, называемой вершиной данной пирамиды. Ее основанием может быть произвольный многоугольник. Грань — это фигура, которая образуется в результате объединения двух ближайших ребер со стороной основания. Гранью пирамиды является треугольник. Расстояние от вершины пирамиды до середины стороны основания называется апофемой. Высотой пирамиды называется длина перпендикуляра, опущенного из вершины к центру ее основания.
Типы пирамид
Различают следующие типы пирамид.
- Прямоугольная — у нее ребро образует угол в 90 градусов с основанием.
- Правильная — ее основание — какой-либо правильный многоугольник, а вершина проецируется в центр этого основания.
- Тетраэдр — пирамида, у которой в основании лежит треугольник.
Формулы объема пирамиды
Объем пирамиды находится несколькими способами.
По площади основания и высоте пирамиды
Простое умножение одной трети площади основания на высоту пирамиды и является ее объемом.
V=13⋅Sосн⋅hV=frac{1}{3}cdot S_{text{осн}}cdot h
SоснS_{text{осн}} — площадь основания пирамиды;
hh — высота данной пирамиды.
Площадь основания пирамиды равна 100 см2100text{ см}^2, а высота ее равна 30 см30text{ см}. Найдите объем тела.
Решение
Sосн=100S_{text{осн}}=100
h=30h=30
Все величины нам известны, подставляем их численные значения в формулу и находим:
V=13⋅Sосн⋅h=13⋅100⋅30=1000 см3V=frac{1}{3}cdot S_{text{осн}}cdot h=frac{1}{3}cdot 100cdot 30=1000text{ см}^3
Ответ
1000 см3.1000text{ см}^3.
Формула объема правильной треугольной пирамиды
Этот способ подходит, если пирамида правильная и треугольная.
V=h⋅a243V=frac{hcdot a^2}{4sqrt{3}}
hh — высота пирамиды;
aa — сторона основания пирамиды.
Вычислите объем правильной треугольной пирамиды, если в ее основании лежит равносторонний треугольник, в котором сторона равна 5 см5text{ см}, а высота пирамиды равна – 19 см19text{ см}.
Решение
a=5a=5
h=19h=19
Просто подставляем данные величины в формулу для объема:
V=h⋅a243=19⋅5243≈68.6 см3V=frac{hcdot a^2}{4sqrt{3}}=frac{19cdot 5^2}{4sqrt{3}}approx68.6text{ см}^3
Ответ
68.6 см3.68.6text{ см}^3.
Формула объема правильной четырехугольной пирамиды
V=13⋅h⋅a2V=frac{1}{3}cdot hcdot a^2
hh — высота пирамиды;
aa — сторона основания пирамиды.
Дана правильная четырехугольная пирамида. Вычислите ее объем, если ее высота равна 7 см7text{ см}, a сторона основания составляет – 2 см2text{ см}.
Решение
a=2a=2
h=7h=7
По формуле вычисляем:
V=13⋅h⋅a2=13⋅7⋅22≈9.3 см3V=frac{1}{3}cdot hcdot a^2=frac{1}{3}cdot 7cdot 2^2approx9.3text{ см}^3
Ответ
9.3 см3.9.3text{ см}^3.
Формула объема тетраэдра
V=2⋅a312V=frac{sqrt{2}cdot a^3}{12}
aa — длина ребра тетраэдра.
Длина ребра тетраэдра равна 13 см13text{ см}. Найдите его объем.
Решение
a=13a=13
Подставляем aa в формулу для объема тетраэдра:
V=2⋅a312=2⋅13312≈259 см3V=frac{sqrt{2}cdot a^3}{12}=frac{sqrt{2}cdot 13^3}{12}approx259text{ см}^3
Ответ
259 см3.259text{ см}^3.
Формула объема пирамиды как определитель
Наверное, самый экзотический способ вычисления объема данного тела.
Пусть даны векторы, на которых построена пирамида как на сторонах. Тогда ее объем будет равен одной шестой смешанного произведения векторов. Последний в свою очередь равен определителю составленному из координат этих векторов. Итак, если пирамида построена на трех векторах:
a⃗=(ax,ay,az)vec{a}=(a_x, a_y, a_z)
b⃗=(bx,by,bz)vec{b}=(b_x, b_y, b_z)
c⃗=(cx,cy,cz)vec{c}=(c_x, c_y, c_z),
тогда объем соответствующей пирамиды это такой определитель:
V=16⋅∣axayazbxbybzcxcycz∣V=frac{1}{6}cdotbegin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}
Найти объем пирамиды через смешанное произведение векторов, координаты которых такие: a⃗=(2,3,5)vec{a}=(2,3,5) , b⃗=(1,4,4)vec{b}=(1,4,4), c⃗=(3,5,7)vec{c}=(3,5,7).
Решение
a⃗=(2,3,5)vec{a}=(2,3,5)
b⃗=(1,4,4)vec{b}=(1,4,4)
c⃗=(3,5,7)vec{c}=(3,5,7)
По формуле:
V=16⋅∣235144357∣=16⋅(2⋅4⋅7+3⋅4⋅3+5⋅1⋅5−5⋅4⋅3−2⋅4⋅5−3⋅1⋅7)=16⋅(56+36+25−60−40−21)=16⋅(−4)=−23≈−0.7V=frac{1}{6}cdotbegin{vmatrix}
2 & 3 & 5 \
1 & 4 & 4 \
3 & 5 & 7 \
end{vmatrix}=frac{1}{6}cdot(2cdot4cdot7 + 3cdot4cdot3 + 5cdot1cdot5 – 5cdot4cdot3 – 2cdot4cdot5 – 3cdot1cdot7) =frac{1}{6}cdot( 56 + 36 + 25 – 60 – 40 – 21)=frac{1}{6}cdot(-4)=-frac{2}{3}approx-0.7
Мы должны взять модуль этого числа, так как объем это неотрицательная величина:
V=0.7 см3V=0.7text{ см}^3
Ответ
0.7 см3.0.7text{ см}^3.
Не знаете, где можно оформить заказ контрольных работ недорого? Наши эксперты помогут вам с решением работ по объемам фигур!
Тест по теме “Объем пирамиды”
Как найти объем пирамиды
Пирамида – это один из частных случаев конуса. Эта пространственная фигура образуется боковыми поверхностями, одна из которых (основание) может иметь любое число углов. Все остальные грани полноразмерной, то есть не усеченной пирамиды, представляют собой треугольники, имеющие с основанием две, а с любой другой боковой гранью не меньше одной общей вершины. Объем пространства, ограниченного такой геометрической фигурой, можно рассчитать несколькими способами.

Инструкция
Если в исходных условиях задачи присутствуют данные о площади основания пирамиды (S) и ее высоте (h), то вам повезло – есть возможность воспользоваться самой простой из формул вычисления объема (V) этой объемной фигуры. Перемножьте оба известных значения, а результат поделите на три: V= S*h.
Если площадь основания не известна, то определите ее, исходя из формул для соответствующих многогранников. Для определения площади основания правильной треугольной формы рассчитайте четверть от произведения квадратного корня из тройки на возведенную в квадрат длину ребра (a) основания. Полученный результат умножьте на треть от высоты (h) пирамиды и ее объем (V) будет найден: V = ¼*√3*a²*⅓*h = √3*a²*h/12.
Если в основании этой объемной фигуры лежит прямоугольник, то сначала найдите его площадь, перемножив длины двух смежных ребер (a и b) основания. Затем, как обычно, умножьте площадь основания на треть от высоты (h) этого многогранника и получите его объем (V): V=⅓*a*b*h.
Используйте такой же алгоритм для нахождения объемов пирамид с основаниями любой другой геометрической формы – вычисляйте площадь основания и умножайте его не одну третью часть высоты фигуры.
Для вычисления объема усеченной пирамиды вам необходимо вычислить площади как основания этой фигуры (S₁), так и ее сечения (S₂). Полученные результаты сложите между собой, а затем прибавьте квадратный корень из произведения этих двух площадей. В заключение получившееся число умножьте на треть высоты (h) пирамиды – на этом нахождение объема (V) будет завершено. В общем виде формулу нахождения объема усеченной пирамиды при известных площадях двух ее параллельных плоскостей можно записать так: V=⅓*h*√(S₁+S₂+(S₁*S₂)).
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Сегодня на уроке мы вспомним, какую фигуру мы
назвали пирамидой, основные элементы пирамиды, выведем формулу для вычисления
объёма пирамиды.
Давайте начнём с того, что вспомним, какую фигуру мы назвали пирамидой.
Определение:
Итак, рассмотрим многоугольник и точку
, не лежащую в
плоскости этого многоугольника. Соединим точку отрезками с вершинами
многоугольника. В итоге получим треугольников:
,
, … ,
. Многогранник,
составленный из -угольника
и этих
треугольников,
называется пирамидой.
Многоугольник называется основанием
пирамиды.
Треугольники ,
, … ,
называются боковыми
гранями пирамиды.
Точка – вершиной
пирамиды, а отрезки ,
, … ,
– её боковыми рёбрами.
Пирамиду с вершиной и
основанием называют
-угольной
пирамидой и обозначают так: .
Отрезок, соединяющий вершину пирамиды с плоскостью её
основания и перпендикулярный к этой плоскости, называется высотой
пирамиды.
Теперь давайте сформулируем и докажем теорему.
Объём пирамиды равен одной трети произведения
площади основания на высоту.
Доказательство.
Сначала давайте докажем теорему для треугольной пирамиды.
Рассмотрим треугольную пирамиду с
объёмом , площадью основания
и
высотой .
Давайте проведём координатную ось так,
чтобы она проходила через высоту пирамиды.
Рассмотрим сечение плоскостью,
перпендикулярной к оси и, значит,
параллельной плоскости основания.
Обозначим через точку точку пересечения
плоскости с осью
,
через обозначим площадь
сечения.
Выразим площадь сечения через площадь
основания пирамиды и высоту пирамиды
.
По рисунку нетрудно увидеть, что . Это действительно
так. Это подобие вытекает из того факта, что сечение параллельно плоскости
основания.
Раз треугольники подобны, значит, отношения .
Рассмотрим прямоугольные треугольники и
. Так как сечение
, значит, отрезки
, отсюда, углы
как соответственные
углы. Значит, треугольники . Поэтому отношения
. Длина отрезка
, то есть отношения
равны.
Поскольку в обоих равенствах присутствует отношение , то можно записать,
что
То есть мы получили, что коэффициент подобия для
треугольников
и
равен
. Тогда площади этих
треугольников относятся .
Теперь давайте применим основную формулу для
вычисления объёмов тел.
Границами интегрирования будут числа 0 и .
Получим, что объём равен .
Теперь давайте докажем эту теорему для произвольной
пирамиды с высотой и площадью основания
. Такую пирамиду можно
разбить на треугольные пирамиды с общей высотой ,
например, пятиугольную пирамиду можно разбить так.
Выразим объём каждой треугольной пирамиды по доказанной формуле.
Мы знаем, что если тело составлено из нескольких
тел, то его объём равен сумме объёмов этих тел. Значит, объём пятиугольной
пирамиды будет равен сумме объёмов треугольных пирамид.
Вынесем за скобку , в скобках получим
сумму площадей оснований треугольных пирамид, а это есть ничто иное как площадь
основания пятиугольной пирамиды.
Таким образом, объём произвольной пирамиды равен . Что и требовалось
доказать.
Следствием из этой теоремы будет формула для
вычисления объёма усечённой пирамиды.
Прежде чем сформулировать это следствие, давайте вспомним,
какую пирамиду мы называем усечённой.
Пусть нам дана пирамида . Проведём секущую
плоскость , параллельную
плоскости основания пирамиды и пусть эта плоскость пересекает боковые рёбра в
точках ,
, …,
. Плоскость
разбивает
пирамиду на две фигуры: пирамиду и многогранник.
Определение:
Многогранник, гранями которого являются
и
, расположенные в
параллельных плоскостях и четырехугольников
,
и так далее
называется усечённой
пирамидой.
-угольники
и
называются
соответственно верхним и нижним основанием.
Четырёхугольники ,
и так далее
называются боковыми
гранями.
,
и так далее
называются боковыми
рёбрами усечённой пирамиды.
Усечённую пирамиду обозначают так .
Возьмём на верхнем основании произвольную точку и
из этой точки опустим перпендикуляр на нижнее основание. Этот перпендикуляр
называется высотой усечённой пирамиды.
Объём усечённой пирамиды, высота которой равна ,
а площадь оснований равны и
, вычисляется по
формуле:
Решим несколько задач.
Задача:
найти объём правильной треугольной пирамиды, высота которой равна ,
а сторона основания равна .
Решение:
поскольку пирамида правильная, значит, в основании лежит правильный, то есть
равносторонний треугольник.
Площадь равностороннего треугольника со стороной 13
см равна .
Применим формулу для вычисления объёма, подставим
числа, выполним элементарные преобразования и получим, что объём призмы равен .
Задача:
в правильной усечённой четырёхугольной пирамиде стороны основания равны и
,
а площадь сечения пирамиды плоскостью, проходящей через два боковых ребра, не
принадлежащих одной грани, равна . Найти объём усеченной
пирамиды.
Решение:
воспользуемся формулой для вычисления объёма усечённой пирамиды.
Площадь оснований этой пирамиды найти нетрудно, эти
площади равны и
.
Рассмотрим сечение пирамиды плоскостью, проходящей
через два боковых ребра, не принадлежащих одной грани. Этим сечением будет
трапеция, причем высота этой трапеции будет высотой усечённой пирамиды, потому
что высотой усечённой пирамиды называется перпендикуляр, опущенный на нижнее
основание.
Высоту мы найдём пользуясь формулой для вычисления
площади трапеции.
Основания трапеции – диагонали квадратов, то есть
основания трапеции соответственно равны и
. Получим, что высота
трапеции равна .
Подставив найденные значения в формулу для
вычисления объёма усечённой пирамиды, мы получим, что объём усечённой пирамиды
равен .
Итоги:
Сегодня на уроке мы вспомнили такие фигуры как
пирамида, усечённая пирамида, вывели формулы для вычисления объёма пирамиды,
усечённой пирамиды. Решили несколько задач.
В данной публикации мы рассмотрим, как можно найти объем пирамиды и разберем примеры решения задач для закрепления материала.
-
Формула вычисления объема пирамиды
-
1. Общая формула
- 2. Объем правильной треугольной пирамиды
- 3. Объем правильной четырехугольной пирамиды
- 4. Объем правильной шестиугольной пирамиды
-
1. Общая формула
- Примеры задач
Формула вычисления объема пирамиды
1. Общая формула
Объем (V) пирамиды равняется одной третьей произведения ее высоты на площадь основания.


- ABCD – основание;
- E – вершина;
- h – высота, перпендикулярная основанию.
2. Объем правильной треугольной пирамиды

Основанием правильной треугольной пирамиды является равносторонний треугольник (ABC), площадь которого вычисляется так (а – сторона треугольника):

Подставляем данное выражение в формулу расчета объема фигуры и получаем:
![]()
3. Объем правильной четырехугольной пирамиды

Основанием правильной четырехугольной пирамиды является квадрат, площадь которого считается так: S = a2, где а – длина его стороны.
Следовательно, формулу объема можно представить в виде:
![]()
4. Объем правильной шестиугольной пирамиды

Основанием правильной шестиугольной пирамиды является правильный шестиугольник, площадь которого вычисляется по формуле (а – сторона основания):
![]()
С учетом этого, объем фигуры считается так:
![]()
Примеры задач
Задание 1
Найдите объем правильной треугольной пирамиды, если известно, что ее высота составляет 16 см, а длина стороны ее основания – 8 см.
Решение:
Воспользуемся соответствующей формулой, подставив в нее известные значения:![]()
Задание 2
Высота правильной четырехугольной пирамиды равна 12 см, а сторона ее основания – 3 см. Найдите объем фигуры.
Решение:
Площадь квадрата, который является основанием пирамиды, равна 9 см2 (3 см ⋅ 3 см). Следовательно, объем равен:![]()

{V= S cdot h}
На этой странице собраны формулы и калькуляторы для нахождения объема пирамиды. Просто введите известные данные в калькулятор и получите результат. Либо рассчитайте объем пирамиды по приведенным формулам самостоятельно.
Пирамида — многогранник, в основании которого лежит многоугольник, а остальные грани представляют собой треугольники, имеющие общую вершину.
Содержание:
- калькулятор объема пирамиды
- формула объема пирамиды
- объем правильной треугольной пирамиды
- объем правильной четырехугольной пирамиды
- объем правильной шестиугольной пирамиды
- объем правильной n-угольной пирамиды
- объем тетраэдра
- примеры задач
Формула объема пирамиды
{V= dfrac{1}{3} S cdot h}
S – площадь основания пирамиды
h – высота пирамиды
Формула объема правильной треугольной пирамиды
Правильная треугольная пирамида – пирамида, в основании которой лежит равносторонний треугольник, а грани являются равнобедренными треугольниками.
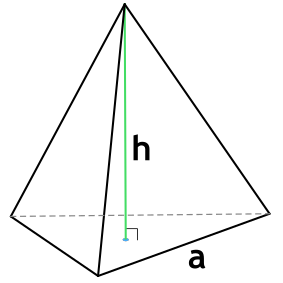
{V= dfrac{h cdot a^2}{4 sqrt{3}}}
a – длина стороны основания пирамиды
h – высота пирамиды
Формула объема правильной четырехугольной пирамиды
Правильная четырехугольная пирамида – пирамида, в основании которой лежит квадрат, а грани являются равнобедренными треугольниками.
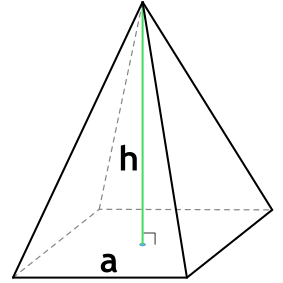
{V= dfrac{1}{3} cdot h cdot a^2}
a – длина стороны основания пирамиды
h – высота пирамиды
Формула объема правильной шестиугольной пирамиды
Правильная шестиугольная пирамида – пирамида, в основании которой лежит правильный шестиугольник, а грани являются равнобедренными треугольниками.
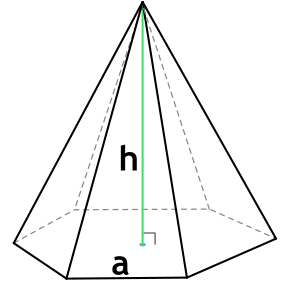
{V= dfrac{sqrt{3}}{2} cdot h cdot a^2}
a – длина стороны основания пирамиды
h – высота пирамиды
Формула объема правильной n-угольной пирамиды
Правильная пирамида имеет в основании правильный многоугольник (все стороны и углы равны между собой), а высота проходит через центр этого основания.

{V= dfrac{n cdot h cdot a^2}{12 cdot tg(dfrac{180°}{n} )}}
a – длина стороны основания пирамиды
h – высота пирамиды
n – число сторон многоугольника в основании пирамиды
Формула объема тетраэдра
Тетраэдр – правильный многогранник (четырехгранник), имеющий четыре грани, каждая из которых является правильным треугольником. У тетраэдра кроме четырех граней также 4 вершины и 6 ребер.
{V= dfrac{sqrt{2} a^3}{12}}
a – длина стороны тетраэдра
Примеры задач на нахождение объема пирамиды
Задача 1
Найдите объем пирамиды с высотой 2м, а основанием ее служит квадрат со стороной 3м.
Решение
Так как в основании пирамиды лежит квадрат, то воспользуемся формулой объема правильной четырехугольной пирамиды и подставим в нее значения высоты и стороны основания.
V= dfrac{1}{3} cdot h cdot a^2 = dfrac{1}{3} cdot 2 cdot 3^2 = dfrac{1}{3} cdot 2 cdot 9 = dfrac{1}{3} cdot 18 = 6 : м^3
Ответ: 6 м³
Используем калькулятор для проверки полученного ответа.
Задача 2
Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1см, а высота равна √3см.
Решение
Из условия следует, что пирамида правильная треугольная. Это значит, что для решения задачи необходимо воспользоваться формулой для правильной треугольной пирамиды. Подставим в нее значения и рассчитаем объем.
V= dfrac{h cdot a^2}{4 sqrt{3}} = dfrac{sqrt{3} cdot 1^2}{4 sqrt{3}} = dfrac{sqrt{3} cdot 1}{4 sqrt{3}} = dfrac{sqrt{3}}{4 sqrt{3}} = dfrac{cancel{sqrt{3}}}{4 cancel{sqrt{3}}} = dfrac{1}{4} = 0.25 : м^3
Ответ: 0.25 см³
Для проверки с помощью калькулятора извлечем квадратный корень из 3: √3 = 1.73205. Теперь можем подставить значения в калькулятор и проверить полученный ответ.
