Коллинеарные векторы
Коллинеарными называются векторы, лежащие на параллельных прямых (или на одной и той же прямой).
Коллинеарные векторы могут иметь одно и то же направление (равнонаправленные векторы) или противоположные направления.
Два ненулевых вектора равны, если они равнонаправлены и имеют один и тот же модуль. Все нулевые векторы считаются равными.
Условие коллинеарности векторов
Если векторы a(x1,y1,z1) и b(x2,y2,z2) коллинеарны, то их соответствующие координаты пропорциональны:
x2/x1 = y2/y1 = z2/z1
И обратно: если соответствующие координаты векторов пропорциональны, то векторы эти — коллинеарны.
Если коэффициент пропорциональности λ = x2/x1 = y2/y1 = z2/z1 положителен, то векторы a и b равнонаправлены, а если отрицателен — то противоположно направлены.
Например:
- векторы АВ(3, 5, 8) и CD(6, 10, 16) коллинеарны;
- векторы АВ(-12, -8, -22) и CD(6, 4, 11) коллинеарны;
- векторы АВ(-10, -8, -21) и CD(6, 5, 11) не коллинеарны
Компланарные векторы
Три вектора (или большее их число) называются компланарными, если они, будучи приведены к общему началу, лежат в одной плоскости.
Если хотя бы один из трёх векторов — нулевой, то три вектора также считаются компланарными.
Компланарность векторов, доказательство их компланарности
Необходимым и достаточным условием компланарности трёх векторов a, b, c является равенство нулю их смешанного произведения.
Например:
- векторы AB(2, 1, 3), CD(-2, 8, 12), EF(3, 15, 27) компланарны;
- векторы AB(-4, 2, -6), CD(-1, -4, 6), EF(-2, 10, -18) компланарны.
Смешанное произведение векторов
Смешанным (или векторно-скалярным) произведением трёх векторов a, b, c называется скалярное произведение вектора а на векторное произведение b×c, т.е. число а(b×c), или, что то же, (b×c)а.
Для того, чтобы найти смешанное произведение трёх векторов a, b и c, заданных своими координатами a(ax,ay,az), b(bx,by,bz), c(cx,cy,cz), нужно определенным образом составить определитель третьего порядка. В первой строке определителя записываем координаты первого вектора, во второй строке — второго, в третьей — третьего:
ax ay az
bx by bz
cx cy cz
и вычисляем определитель. Результат вычислений и есть искомое смешанное произведение трёх векторов.
Например, смешанное произведение векторов a(-2, 5, -3), b(1, -4, 6), c(1, 5, 9) равно 90.
Смешанное произведение abc трех некомпланарных векторов a, b, c равно объёму параллелепипеда, построенного на векторах a, b, c, взятому со знаком «плюс», если система a, b, c — правая, и со знаком «минус», если эта система левая.
Иногда вопрос задают так: «Чему равен объём параллелепипеда, построенного на векторах a, b и c?». Как уже известно, равен он смешанному произведению векторов a, b и c. Если результат окажется со знаком «минус», то результат, конечно же, нужно взять по модулю.
Например, объём параллелепипеда, построенного на векторах a(-2, 5, -3), b(1, -4, 6), c(1, 5, 9), равен 90 кубических единиц.
Объём пирамиды, построенной на векторах
Объём пирамиды, построенной на векторах a, b и c, равен 1/6 объёма параллелепипеда, построенного на векторах a, b и c.
Если известны координаты вершин A, B, C, D пирамиды, то последовательность действий для нахождения её объёма следующая:
- находим координаты векторов AB, AC и AD;
- находим 1/6 смешанного произведения векторов AB, AC и AD (результат вычислений берём со знаком «плюс»).
Например, даны вершины пирамиды ABCD:
- A(5, 0, 14);
- B(-7, 16, 9);
- C(14, -5, 17);
- D(15, 11, -2).
Находим координаты векторов AB, AC и AD:
- AB = (-7-5, 16-0, 9-14) = (-12, 16, -5);
- AC = (14-5, -5-0, 17-14) = (9, -5, 3);
- AD = (15-5, 11-0, -2-14) = (10, 11, -16).
Вычисляем 1/6 смешанного произведения векторов AB, AC и AD.
V = 1/6 · 1475 = 245,83 кубических единиц.
Источники:
- М.Я. Выгодский. Справочник по высшей математике.
- В.Д. Черненко. Высшая математика в примерах и задачах. В 3 томах. Том 1.
Дополнительно на Геноне:
- Что такое определитель матрицы?
- Как найти определитель матрицы?
- Какими свойствами обладает определитель матрицы?
Часто в задачах школьного курса геометрии приходится решать задания, которые требуют использования комплексного подхода. Одной из таких задач является вычисление объема пирамиды по координатам вершин. Как решить эту геометрическую задачу – ответит приведенная ниже статья.
Что представляет собой пирамида?
Говоря простыми словами, под этой фигурой понимают пространственный объект, ограниченный треугольными сторонами и одной многоугольной гранью, которая называется основанием. Многоугольное основание может быть произвольным n-угольником на плоскости, например, правильным треугольником, параллелограммом и так далее.
Любая пирамида имеет n + 1 грань, 2 * n ребер и n + 1 вершину. Вершины фигуры не являются равноправными. Так, существует единственная вершина, которая не принадлежит основанию. Она называется главной. Расстояние от нее до плоскости основания – это высота фигуры.
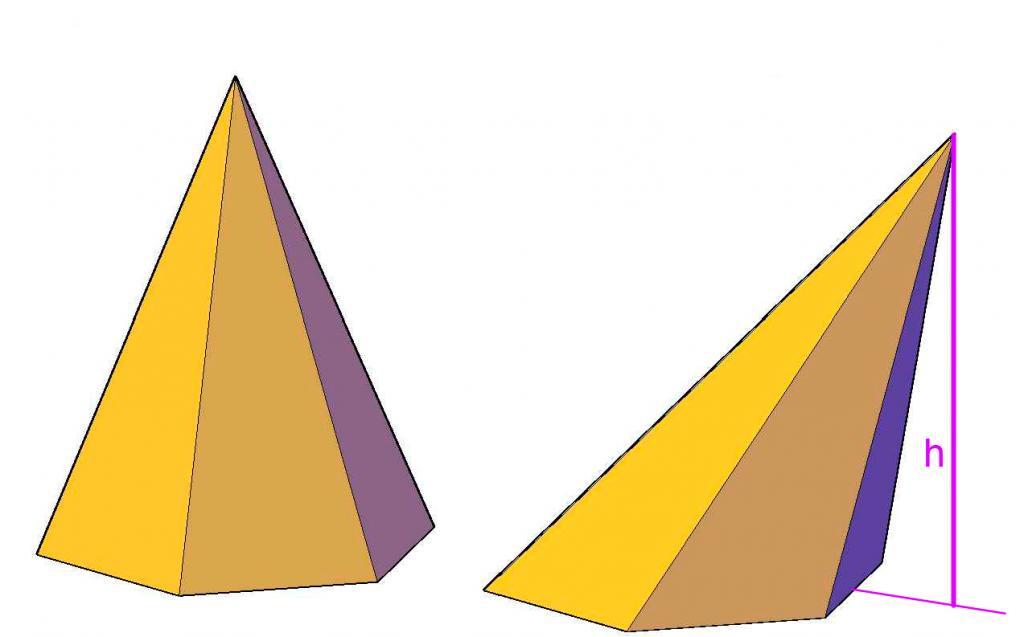
Пирамиды могут быть наклонными, если высота пересекает основание не в его центре, или прямыми, когда высота с основанием пересекается в геометрическом центре последнего. Также фигуры могут быть неправильными и правильными. Пирамиды правильные состоят из равноугольного и равностороннего основания и нескольких равнобедренных треугольников, которые друг другу равны.
Как рассчитывается объем пирамиды?
Прежде чем приводить методику вычисления по координатам вершин объема пирамиды, следует привести формулу, при помощи которой можно рассчитать эту величину для фигуры любого типа из рассматриваемого класса. Итак, объем пирамиды рассчитывается так:
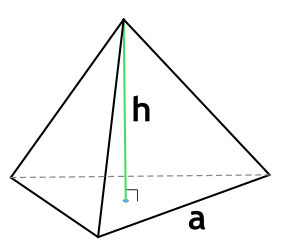
V = 1 / 3 * So * h.
Здесь So – это основания площадь, h – расстояние от главной вершины до основания, то есть высота пирамиды.
Таким образом, любая геометрическая задача на нахождение объема пирамиды сводится к расчету величин So и h.
Как найти объем пирамиды по координатам вершин: методика
Пирамида может быть представлена произвольным n-угольным основанием. Чтобы рассчитать его площадь, следует внимательно изучить условие задачи, в котором должно быть сказано, о каком типе n-угольника идет речь. Если это треугольник или параллелограмм, то расчет его площади по известным координатам очень прост: необходимо лишь найти векторное произведение соответствующих векторов сторон.
Вычислить высоту пирамиды также не представляет особого труда. Для этого следует из любых трех точек основания получить уравнение плоскости в общем виде, а затем нужно воспользоваться формулой расстояния между плоскостью и точкой (вершиной пирамиды). Формула имеет вид:
d = |(A * x1 + B * y1 + C * z1 + D)| / √(A2 + B2 + C2).
Здесь (x1; y1; z1) – координаты точки.
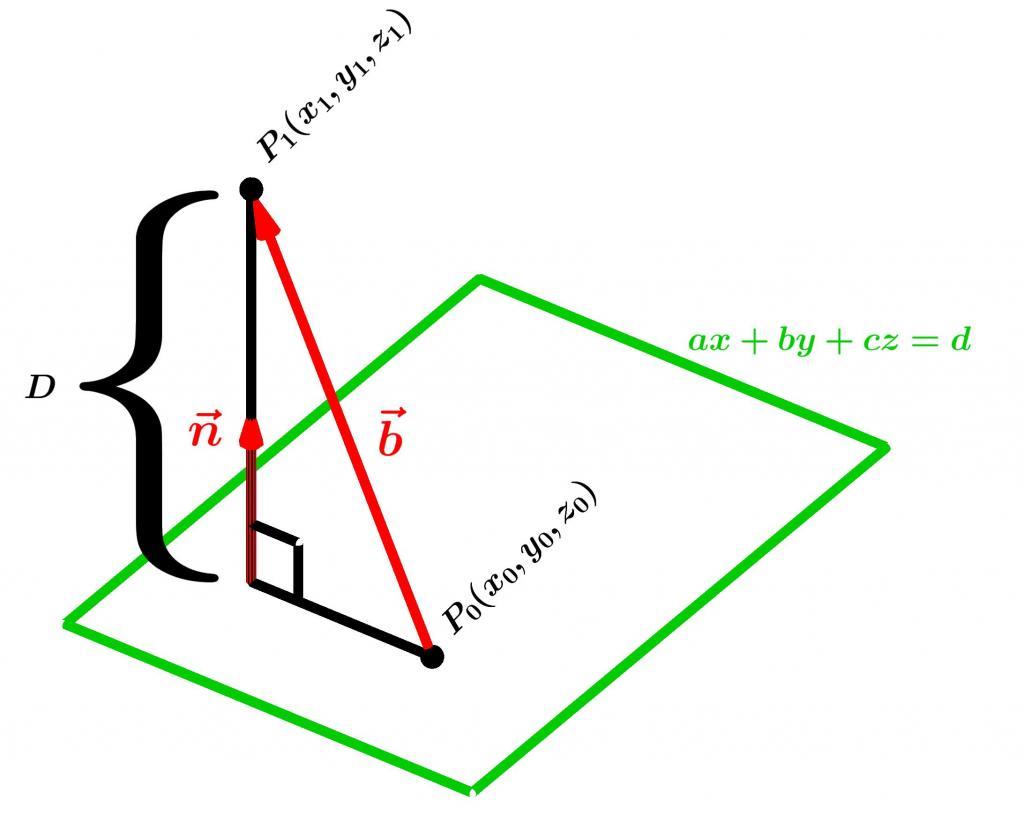
Уравнение плоскости имеет вид:
A * x + B * y + C * z + D = 0.
Задача с треугольной пирамидой

Решим задачу на примере самой простой пирамиды – треугольной. Условие простое: ниже даны координаты вершин пирамиды, объем найти нужно для фигуры, которая на этих координатах построена:
- A(1; 0; 3);
- B(0; 2; -1);
- C(3; 3; 1);
- D(4; 3; 4).
Положим, что основание пирамиды является треугольником ABC. Найдем длины векторов AB¯ и AC¯:
AB¯ = (-1; 2; -4);
AC¯ = (2; 3; -2).
Векторное произведение AB¯ и AC¯ даст нам, с одной стороны, двойную площадь треугольника, то есть 2 * So, а с другой стороны, мы получим координаты нормального к плоскости вектора n¯, имеем:
n¯ = [AB¯ * AC¯] = (8; -10; -7).
Площадь треугольного основания равна полудлине вектора n¯, то есть:
So = √(82 + 102 + 72) / 2 = 7,3.
Прежде чем рассчитывать расстояние от D до плоскости ABC, необходимо записать уравнение плоскости. Три его коэффициента (A, B, C) мы уже знаем, они соответствуют координатам нормали n¯. Свободный член можно получить, подставив в уравнение координаты любой точки плоскости, например точки A, имеем:
D = -1 * (A * x1 + B * y1 + C * z1) = -1 * (8 * 1 + (-10) * 0 + (-7) * 3) = 13.
Тогда уравнение плоскости основания пирамиды принимает форму:
8 * x – 10 * y – 7 * z + 13 = 0.
Теперь применяем приведенную выше формулу для расчета расстояния от точки D(4; 3; 4) до найденной плоскости, получаем:
d = |(8 * 4 – 10 * 3 – 7 * 4 + 13)| / √(82 + 102 + 72) = 0,89.
Поскольку найденное значение расстояния d соответствует высоте пирамиды треугольной h, то можно воспользоваться формулой для объема фигуры:
V = 1 / 3 * So * h = 1 / 3 * 7,3 * 0,89 ≈ 2,166.
Полученное значение объема выражено в кубических единицах выбранной координатной системы.
Аналитическая геометрия – задача на расчет пирамиды (тетраэдра)
Краткая теория
Вузовская аналитическая геометрия отличается от курса школьной геометрии. Главное отличие состоит в том, что она основным своим инструментом имеет набор алгебраических формул и методов вычислений. В основе аналитической геометрии лежит метод координат.
Аналитическая геометрия имеет набор формул, готовых уравнений и алгоритмов действия. Для успешного и правильного решения главное – разобраться и уделить задаче достаточно времени.
Данная задача является типовой в курсе аналитической геометрии и требует использования различных методов и знаний, таких как декартовые прямоугольные координаты и вектора в пространстве.
Пример решения задачи
Задача
Даны координаты
вершин пирамиды
. Найти:
Сделать чертеж.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
Длина ребра
Длину ребра
найдем по
формуле расстояния между 2-мя точками:
Угол между ребрами
Угол между ребрами
и
найдем как угол
между направляющими векторами
и
:
Косинус угла между
векторами:
Угол между ребром и гранью. Векторное произведение
Вычислим угол между
ребром
и гранью
.
Для этого вычислим
координаты нормального вектора плоскости
–им будет
векторное произведение векторов
и
.
Найдем векторное произведение. Для этого
вычислим определитель:
Нормальный вектор
плоскости:
Синус угла:
Площадь грани
Вычислим площадь
грани
. Она будет численно равна половине модуля векторного
произведения векторов
и
:
Искомая площадь:
Объем пирамиды. Смешанное произведение векторов
Вычислим объем
пирамиды. Он будет равен шестой части модуля смешанного произведения векторов
и
:
Для того чтобы вычислить смешанное произведение, необходимо
найти определитель квадратной матрицы, составленной из координат векторов:
Искомый объем
пирамиды:
Уравнение прямой в пространстве
Вычислим уравнение
прямой
. Направляющим
вектором искомой прямой является вектор
. Кроме того, прямая проходит через точку
Уравнение искомой
прямой:
Уравнение плоскости
Вычислим уравнение
плоскости
. Нормальный вектор плоскости
. кроме того, плоскость проходит через точку
-уравнение
грани
Уравнение высоты, опущенной на грань
Составим уравнение
высоты, опущенной на грань
из вершины
:
Нормальный вектор
является
направляющим вектором высоты, кроме того, высота проходит через точку
Искомое уравнение
высоты:
Сделаем схематический чертеж:

{V= S cdot h}
На этой странице собраны формулы и калькуляторы для нахождения объема пирамиды. Просто введите известные данные в калькулятор и получите результат. Либо рассчитайте объем пирамиды по приведенным формулам самостоятельно.
Пирамида — многогранник, в основании которого лежит многоугольник, а остальные грани представляют собой треугольники, имеющие общую вершину.
Содержание:
- калькулятор объема пирамиды
- формула объема пирамиды
- объем правильной треугольной пирамиды
- объем правильной четырехугольной пирамиды
- объем правильной шестиугольной пирамиды
- объем правильной n-угольной пирамиды
- объем тетраэдра
- примеры задач
Формула объема пирамиды
{V= dfrac{1}{3} S cdot h}
S – площадь основания пирамиды
h – высота пирамиды
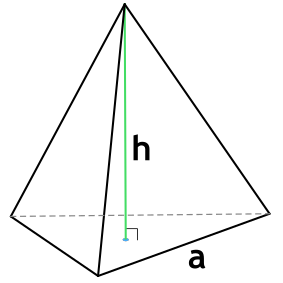
Формула объема правильной треугольной пирамиды
Правильная треугольная пирамида – пирамида, в основании которой лежит равносторонний треугольник, а грани являются равнобедренными треугольниками.
{V= dfrac{h cdot a^2}{4 sqrt{3}}}
a – длина стороны основания пирамиды
h – высота пирамиды
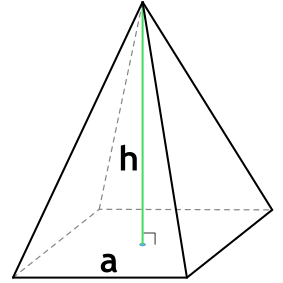
Формула объема правильной четырехугольной пирамиды
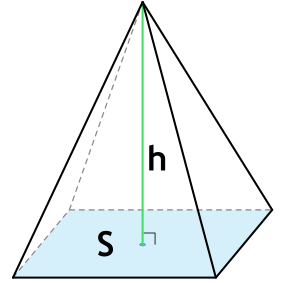
Правильная четырехугольная пирамида – пирамида, в основании которой лежит квадрат, а грани являются равнобедренными треугольниками.
{V= dfrac{1}{3} cdot h cdot a^2}
a – длина стороны основания пирамиды
h – высота пирамиды
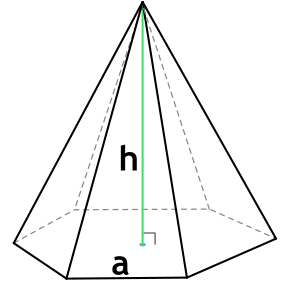
Формула объема правильной шестиугольной пирамиды
Правильная шестиугольная пирамида – пирамида, в основании которой лежит правильный шестиугольник, а грани являются равнобедренными треугольниками.
{V= dfrac{sqrt{3}}{2} cdot h cdot a^2}
a – длина стороны основания пирамиды
h – высота пирамиды
Формула объема правильной n-угольной пирамиды
Правильная пирамида имеет в основании правильный многоугольник (все стороны и углы равны между собой), а высота проходит через центр этого основания.
{V= dfrac{n cdot h cdot a^2}{12 cdot tg(dfrac{180°}{n} )}}
a – длина стороны основания пирамиды
h – высота пирамиды
n – число сторон многоугольника в основании пирамиды
Формула объема тетраэдра
Тетраэдр – правильный многогранник (четырехгранник), имеющий четыре грани, каждая из которых является правильным треугольником. У тетраэдра кроме четырех граней также 4 вершины и 6 ребер.
{V= dfrac{sqrt{2} a^3}{12}}
a – длина стороны тетраэдра
Примеры задач на нахождение объема пирамиды
Задача 1
Найдите объем пирамиды с высотой 2м, а основанием ее служит квадрат со стороной 3м.
Решение
Так как в основании пирамиды лежит квадрат, то воспользуемся формулой объема правильной четырехугольной пирамиды и подставим в нее значения высоты и стороны основания.
V= dfrac{1}{3} cdot h cdot a^2 = dfrac{1}{3} cdot 2 cdot 3^2 = dfrac{1}{3} cdot 2 cdot 9 = dfrac{1}{3} cdot 18 = 6 : м^3
Ответ: 6 м³
Используем калькулятор для проверки полученного ответа.
Задача 2
Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1см, а высота равна √3см.
Решение
Из условия следует, что пирамида правильная треугольная. Это значит, что для решения задачи необходимо воспользоваться формулой для правильной треугольной пирамиды. Подставим в нее значения и рассчитаем объем.
V= dfrac{h cdot a^2}{4 sqrt{3}} = dfrac{sqrt{3} cdot 1^2}{4 sqrt{3}} = dfrac{sqrt{3} cdot 1}{4 sqrt{3}} = dfrac{sqrt{3}}{4 sqrt{3}} = dfrac{cancel{sqrt{3}}}{4 cancel{sqrt{3}}} = dfrac{1}{4} = 0.25 : м^3
Ответ: 0.25 см³
Для проверки с помощью калькулятора извлечем квадратный корень из 3: √3 = 1.73205. Теперь можем подставить значения в калькулятор и проверить полученный ответ.
Как найти объем пирамиды, если даны координаты вершин
Для расчета объема пирамиды можно воспользоваться постоянным соотношением, связывающим эту величину с объемом параллелепипеда, построенного на том же основании и с таким же наклоном высоты. А объем параллелепипеда рассчитывается достаточно просто, если представить его ребра как набор векторов – наличие в условиях задачи координат вершин пирамиды позволяет это сделать.

Инструкция
Рассматривайте ребра пирамиды как векторы, на которых построена эта фигура. По координатам точек в вершинах A(X₁;Y₁;Z₁), B(X₂;Y₂;Z₂), C(X₃;Y₃;Z₃), D(X₄;Y₄;Z₄), определите проекции векторов, исходящих из вершины пирамиды, на оси ортогональной системы координат – вычтите из каждой координаты конца вектора соответствующую координату начала: AB{X₂-X₁;Y₂-Y₁;Z₂-Z₁}, AC{X₃-X₁;Y₃-Y₁;Z₃-Z₁}, AD{X₄-X₁;Y₄-Y₁;Z₄-Z₁}.
Воспользуйтесь тем, что объем параллелепипеда, построенного на этих же векторах, должен быть в шесть раз больше объема пирамиды. Объем такого параллелепипеда определить нетрудно – он равен смешанному произведению векторов: |AB*AC*AD|. Значит, объем пирамиды (V) составит одну шестую часть от этой величины: V = ⅙*|AB*AC*AD|.
Для расчета смешанного произведения из полученных на первом шаге координат составьте матрицу, поместив в каждую ее строку три координаты соответствующего вектора:
(X₂-X₁) (Y₂-Y₁) (Z₂-Z₁)
(X₃-X₁) (Y₃-Y₁) (Z₃-Z₁)
(X₄-X₁) (Y₄-Y₁) (Z₄-Z₁)
Затем рассчитайте ее определитель – построчно перемножьте все элементы множества и сложите результаты:
(X₂-X₁)*(Y₃-Y₁)*(Z₄-Z₁) + (Y₂-Y₁)*(Z₃-Z₁)*(X₄-X₁) + (Z₂-Z₁)*(X₃-X₁)*(Y₄-Y₁) + (Z₂-Z₁)*(Y₃-Y₁)*(X₄-X₁) + (Y₂-Y₁)*(X₃-X₁)*(Z₄-Z₁) + (X₂-X₁)*(Z₃-Z₁)*(Y₄-Y₁).
Полученное на предыдущем шаге значение соответствует объему параллелепипеда – разделите его на шестерку, чтобы получить искомый объем пирамиды. В общем виде эту громоздкую формулу можно записать так: V = ⅙*|AB*AC*AD| = ⅙*((X₂-X₁)*(Y₃-Y₁)*(Z₄-Z₁) + (Y₂-Y₁)*(Z₃-Z₁)*(X₄-X₁) + (Z₂-Z₁)*(X₃-X₁)*(Y₄-Y₁) + (Z₂-Z₁)*(Y₃-Y₁)*(X₄-X₁) + (Y₂-Y₁)*(X₃-X₁)*(Z₄-Z₁) + (X₂-X₁)*(Z₃-Z₁)*(Y₄-Y₁)).
Если ход вычислений в решении задачи приводить не требуется, а нужно лишь получить численный результат, проще воспользоваться для расчетов онлайн-сервисами. В сети нетрудно найти скрипты, которые могут помочь с промежуточными расчетами – посчитать детерминант матрицы – или самостоятельно вычислить объем пирамиды по введенным в поля формы координатам точек. Пара ссылок на такие сервисы приведена ниже.
Источники:
- Расчет объема пирамиды по координатам
- объем пирамиды через координаты вершин
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.