Как рассчитать объем пирамиды
На данной странице калькулятор поможет рассчитать объем пирамиды онлайн. Для расчета задайте площадь, высоту, сторону или количество сторон. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. Пирамида является частным случаем конуса. Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания.
Пирамида
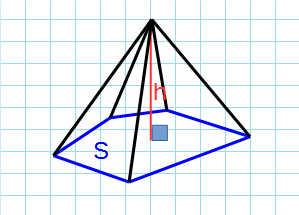
Формула объема пирамиды через высоту и площадь основания:
S – площадь основания; h – высота пирамиды.
Правильная пирамида
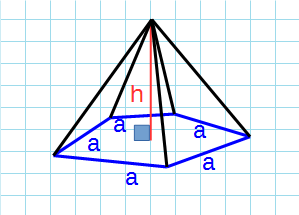
Правильная пирамида — пирамида, в основании которой лежит правильный многоугольник, а высота проходит через центр основания.
Формула объема правильной пирамиды через сторону основания, высоту и количество сторон:
a – сторона основания; h – высота пирамиды; n – количество сторон многогранника в основании.
Правильная треугольная пирамида
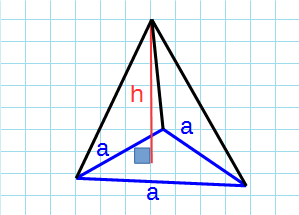
Правильная треугольная пирамида — пирамида, у которой основанием является равносторонний треугольник и грани равные равнобедренные треугольники.
Формула объема правильной треугольной пирамиды через сторону основания и высоту:
a – сторона основания; h – высота пирамиды.
Правильная четырехугольная пирамида
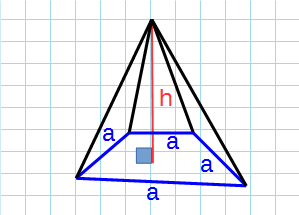
Правильная четырехугольная пирамида — пирамида, у которой основанием является квадрат и грани равные равнобедренные треугольники.
Формула объема правильной четырехугольной пирамиды через сторону основания и высоту:
a – сторона основания; h – высота пирамиды.
Тетраэдр
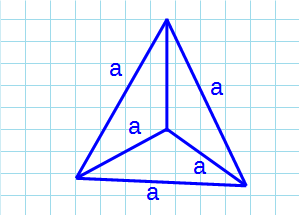
Тетраэдр — пирамида, у которой все грани равносторонние треугольники.
Формула объема тетраэдра:
a – ребро тетраэдра.
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Что считает калькулятор
Калькулятор объема пирамиды — это онлайн инструмент, который используется для быстрого расчета объема пирамиды по ее известным параметрам. Объем пирамиды представляет собой объем пространства, которое занимает эта фигура в трехмерном пространстве.
Калькулятор объема пирамиды может быть полезным инструментом для учебных заданий или практических задач, связанных с расчетами объемов таких геометрических фигур. Он также может использоваться в различных профессиональных областях, где необходимы точные расчеты объемов, например, в архитектуре, инженерии, физике и т.д.
Где можно применить калькулятор объема пирамиды
Калькулятор объема пирамиды можно применить в различных сферах, где требуется вычислить объем пирамиды, например:
- Строительство: при проектировании зданий и сооружений инженерам и архитекторам часто нужно вычислить объем пирамиды, например, для расчета объема кровли или фундамента.
- Геометрия: в математике пирамиды являются важным объектом изучения, и вычисление их объема – одна из основных задач геометрии.
- Производство: в производстве может потребоваться вычислить объем пирамиды для расчета необходимых материалов, например, для производства упаковки.
- Учебные цели: калькулятор объема пирамиды может быть использован студентами и учениками при изучении геометрии или математики.
- Игры и развлечения: калькулятор объема пирамиды может быть использован в играх и развлечениях, где требуется решить задачу по вычислению объема пирамиды.
В целом, калькулятор объема пирамиды может быть полезен во всех ситуациях, где требуется вычислить объём данной фигуры.
В чем преимущество пирамиды
Пирамида — многогранник, основание которого является многоугольником, а остальные грани – треугольниками, имеющими общую вершину.
Пирамидальная форма имеет несколько преимуществ:
- Стабильность. Пирамида имеет широкое основание и суживающийся верх, что делает ее очень стабильной. Это свойство делает пирамиду идеальным выбором для многих инженерных и архитектурных конструкций.
- Эффективность использования пространства. Пирамидальная форма позволяет использовать пространство более эффективно. Благодаря своей форме пирамида может поместить больше материала на меньшей площади, чем другие формы.
- Видимость. Пирамиды обычно имеют значительную высоту и суживающуюся вершину, что делает их легко заметными издалека. Это свойство делает пирамиды идеальным выбором для монументальных сооружений, таких как пирамиды в Египте или Латинской Америке.
- Эстетика. Пирамидальная форма может быть очень эстетичной и привлекательной. Она может использоваться в различных областях, таких как дизайн зданий, декоративное искусство, упаковка продуктов и многое другое.
В целом, пирамидальная форма имеет множество преимуществ, которые делают ее полезной в различных областях. Однако, как и любая другая форма, она может иметь свои недостатки в зависимости от контекста, в котором она используется.
Как вычислить объем пирамиды
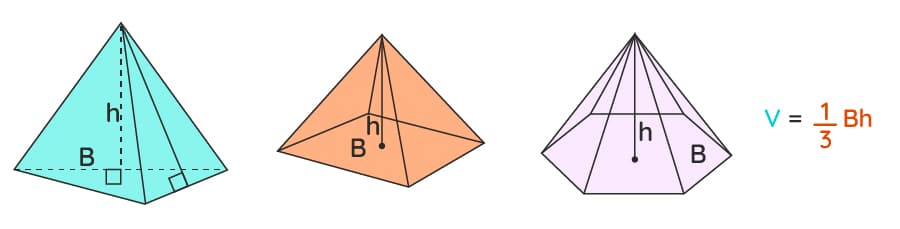
Калькулятор объема пирамиды использует стандартные математические формулы для расчета объема пирамиды с основанием любой формы.
Как вычислить объем пирамиды по высоте и площади основания
Формула расчета объема пирамиды, которая основана на ее высоте и площади основания, выглядит следующим образом:
V = 1/3 * S * h
где: V – объем пирамиды S – площадь основания пирамиды h – высота пирамиды
Для того, чтобы вычислить объем пирамиды, нужно знать ее высоту и площадь основания. Подставьте известные значения в соответствующие поля калькулятора и получите необходимое значение объема.
Например, для пирамиды с площадью основания 20см2 и высотой 5см расчёт объема будет выглядеть таким образом:
V = 1/3 * S * h = 1/3 * 20 * 5 = 33.3см3
Как вычислить объем пирамиды с правильным многоугольным основанием
Правильная пирамида – это пирамида, в основании которой лежит правильный многоугольник, а высота проходит через центр вписанной в основание окружности.
Объем пирамиды с правильным многоугольным основанием можно вычислить по формуле:
V = (n * a2 * h) / (12 * tan(180о/n))
где h – высота пирамиды, а – сторона основания, n – количество сторон в основании
Например, объем правильной многоугольной пирамиды с высотой 100см, стороной основания 12см и количеством сторон 6 равен:
V = (n * a2 * h) / (12 * tan(180о/n)) = (6 * 122 * 100) / (12 * tan(180о/6)) = 12470.7658см3
Как вычислить объем правильной треугольной пирамиды
Правильная треугольная пирамида – это пирамида, у которой основанием является равносторонний треугольник и грани равные равнобедренные треугольники.
Объем пирамиды с правильным треугольным основанием можно вычислить по формуле:
V = h * a² / 4 * √3
где h – высота пирамиды, а – сторона основания
Таким образом, чтобы вычислить объем правильной треугольной пирамиды, необходимо знать длину стороны основания и длину ее высоты, и затем использовать вышеуказанную формулу.
Например, объем правильной треугольной пирамиды с высотой 100см и стороной основания 12см равен:
V = h * a² / 4 * √3 = 100 * 12² / 4 * √3 = 2078.461см3
Как вычислить объем правильной четырехугольной пирамиды
Правильная четырехугольная пирамида – это пирамида, у которой основанием является квадрат и грани равные равнобедренные треугольники.
Объем пирамиды с правильным четырехугольным основанием можно вычислить по формуле:
V = 1 / 3 * h * a²
где h – высота пирамиды, а – сторона основания.
Таким образом, чтобы вычислить объем правильной треугольной пирамиды, необходимо знать длину стороны основания и длину ее высоты, и затем использовать вышеуказанную формулу.
Например, объем правильной четырехугольной пирамиды с высотой 100см и стороной основания 12см равен:
V = 1 / 3 * h * a² = 1 / 3 * 100 * 12² = 4800см3
Как вычислить объем тетраэдра
Тетраэдр – пирамида, у которой все грани – равносторонние треугольники.
Объем пирамиды с правильным треугольным основанием можно вычислить по формуле:
V = a3 * √2 / 12
где а – сторона основания.
Таким образом, чтобы вычислить объем правильной треугольной пирамиды, необходимо знать длину стороны основания, и затем использовать вышеуказанную формулу.
Например, объем тетраэдра со стороной основания 12см равен:
V = a3 * √2 / 12 = 123 * √2 / 12 = 203.6468см3
❓ Вопросы и ответы
А вот несколько ответов на часто задаваемы вопросе о пирамиде и ее параметрах.
Как найти площадь основания пирамиды?
Площадь основания пирамиды зависит от ее формы. Если основание пирамиды имеет форму прямоугольника, площадь вычисляется по формуле S = a * b, где a и b – длины сторон прямоугольника. Если основание пирамиды имеет форму треугольника, площадь вычисляется по формуле S = (a * b * sin(α)) / 2, где a и b – длины сторон треугольника, α – угол между ними.
Как определить высоту пирамиды?
Высоту пирамиды можно определить с помощью теоремы Пифагора. Для этого необходимо построить прямую, проходящую через вершину пирамиды и перпендикулярную к основанию. Затем нужно измерить длину этой прямой и длину отрезка, соединяющего середины двух сторон основания. Высота пирамиды равна квадратному корню из разности квадратов этих длин.
Как найти боковую поверхность пирамиды?
Боковая поверхность пирамиды состоит из треугольников, каждый из которых имеет общую вершину в вершине пирамиды и стороны, соединяющие эту вершину с точками на основании. Площадь каждого такого треугольника можно вычислить по формуле S = (a * h) / 2, где a – длина стороны основания, h – высота боковой грани. Общая площадь боковой поверхности пирамиды равна сумме площадей всех ее боковых граней.
Как вычислить полную поверхность пирамиды?
Для вычисления полной поверхности пирамиды нужно сложить площади всех ее боковых граней и площадь ее основания. Формула для вычисления площади боковой грани зависит от формы пирамиды. Например, если пирамида имеет правильную многоугольную основу, то ее боковые грани будут равными равнобедренными треугольниками. Площадь такой грани можно вычислить по формуле: Sбок = (1/2) * Периметр основания * Высота боковой грани, где Периметр основания – периметр многоугольной основы пирамиды, Высота боковой грани – расстояние от вершины пирамиды до середины ребра ее основания.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
- Калькулятор площади трапеции. Рассчитайте онлайн площадь трапеции, не только зная длины ее оснований и высоту, но и по другим известным параметрам, например, диагоналям.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Объём пирамиды онлайн калькулятор
Онлайн калькулятор вычиселения объема пирамиды может вычислить объем пирамиды различными способами:
- По площади основания и высоте для пирамиды любой формы,
- По числу сторон и высоте для правильной пирамиды,
- По стороне и высоте для треугольной, четырехугольной и шестиугольной пирамиды.
Объем пирамиды можно легко вычислить на этом онлайн калькуляторе.
Вы получите ответ в развернутом виде шаг за шагом. Тем самым усвоете материал по данной теме.
- Калькулятор
- Инструкция
- Теория
- История
- Сообщить о проблеме
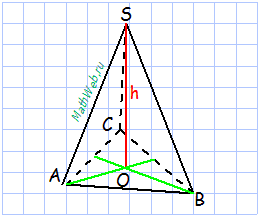
В основании правильной треугольной пирамиды лежит равносторонний треугольник.
Формула объема пирамиды: 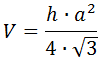
где a – длина одной из сторон основания,h – высота пирамиды.
Решение:
V =
=
=
0.722
Ответ: Объём правильной треугольной пирамиды с длиной стороны основания a = 1 и высотой h = 5 равен 0.722
Многогранник, у которого одна грань многоугольник, а все остальные грани — треугольники с общей вершиной, называется пирамидой.
Многоугольная грань пирамиды называется ее основанием, треугольные грани с общей вершиной — боковыми гранями, а их общая вершина — вершиной пирамиды.
Похожие калькуляторы
-
Объём тетраэдра онлайн калькулятор
-
Объём цилиндра онлайн калькулятор (3 способа)
-
Объём шара онлайн калькулятор (3 способа)
-
Объём призмы онлайн калькулятор
-
Объём параллелепипеда онлайн калькулятор (3 способа)
Калькуляторы других категорий
-
Деление в столбик онлайн. Калькулятор наглядного деления.
-
Перевод чисел из одной системы счисления в любую другую онлайн
-
Сторона треугольника 14 формул расчет онлайн
-
Сложение, умножение и деление чисел в различных системах счисления
-
Умножение в столбик онлайн. Калькулятор наглядного умножения.
Объем пирамиды – это характеристика объемного геометрического тела, указывающая на то, сколько внутри фигуры может вместиться единичных кубических элементов. Если вычисляется объем пирамиды Хеопса, единицей объема могут быть кубические метры.
Если рассматривается небольшая оптическая деталь того или иного проектируемого прибора, имеющая форму пирамиды, единицей измерения объема пирамиды могут быть кубические миллиметры. Калькулятор осуществляет вычисление объема пирамиды, основываясь на формуле, в которой исходными данными является высота и площадь основания: V = (1/3) х S х h. Исходные данные нужно задавать в одинаковых единицах меры длины.
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Калькулятор объёма пирамиды
Калькулятор объёма пирамиды
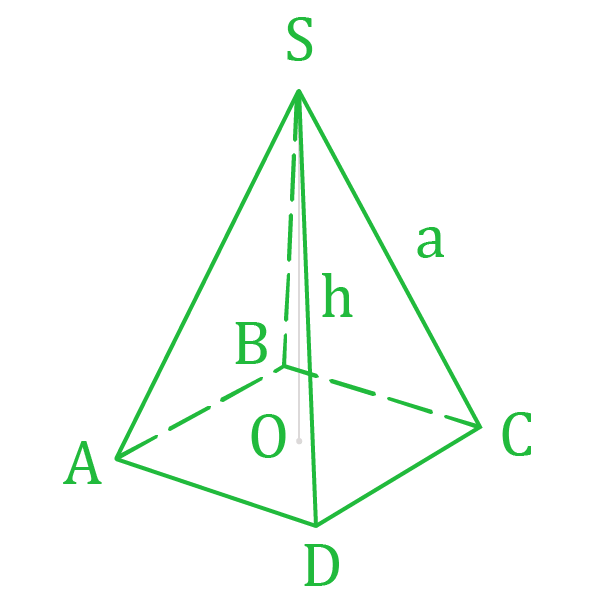
Расчёт объёма пирамиды
Введите размеры в мм:
Площадь, s:
Неверный ввод
Длина стороны, a:
Неверный ввод
Кол-во сторон:
Неверный ввод
Сторона, а:
Неверный ввод
Сторона, а:
Неверный ввод
Сторона, а:
Неверный ввод
Выводим результат в:
Неверный ввод
Решение по формуле:
Формула объема пирамиды через высоту и площадь основания:
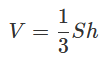
S – площадь основания; h – высота пирамиды.
Формула объема правильной пирамиды через сторону основания, высоту и количество сторон:
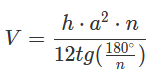
a – сторона основания; h – высота пирамиды; n – количество сторон многогранника в основании.
Формула объема правильной треугольной пирамиды через сторону основания и высоту:
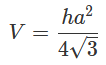
a – сторона основания; h – высота пирамиды.
Формула объема правильной четырехугольной пирамиды через сторону основания и высоту:
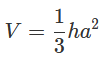
a – сторона основания; h – высота пирамиды.
Формула объема тетраэдра:
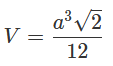
a – ребро тетраэдра.
Скачать, сохранить результат
Выберите способ сохранения
-
Вы можете сохранить результат расчёта в формате PDF на ваше устройство.
-
Распечатайте результат расчёта конструкции на бумагу любого формата.
-
Отправьте результат расчета в формате PDF на ваш е-мейл.
Информация
Формула объема пирамиды является одним из базовых понятий в геометрии. Без этого понятия буквально не существовало бы строительства, многих видов техники и технологий, поскольку все они базируются на основных законах математики. Люди, которые используют подобные формулы в профессиональной деятельности, несут большую ответственность, когда осуществляют расчеты. Это связанно с тем, что малейший просчет в строительстве (например) может повлечь за собой катастрофические последствия.
Для того, чтобы снять лишнюю нагрузку с ответственных сотрудников, мы создали калькулятор, который позволит с предельной точностью посчитать хоть объем усеченной пирамиды, хоть любой другой показатель. Теперь специалисты могут, не теряя лишнего времени, рассчитывать необходимый показатель, например, объем треугольной пирамиды. Наш онлайн калькулятор позволяет не только рассчитать необходимый показатель, но и предоставляет формулы, по которым данный показатель находится. Вы сразу сможете посмотреть как найти объем пирамиды.
Чтобы рассчитать объем пирамиды на нашем калькуляторе, Вам необходимо:
- Выбрать вид пирамиды, объем которой необходимо найти (например, объем правильной четырехугольной пирамиды).
- Ввести запрашиваемые калькулятором данные в соответствующие поля.
- Выбрать единицы исчисления результата (см3, литры, м3).
- Получить точный результат, правильность которого гарантирована.
Какую же пользу получает пользователь от нашего онлайн-калькулятора?
- Экономия времени благодаря отсутствию необходимости в проведении самостоятельных расчетов (например, не нужно самому считать объем шестиугольной пирамиды по формулам).
- Максимально точный результат, верность которого обоснована автоматизацией калькулятора и наглядностью применяемых им формул, когда каждая формула представлена на экране.
- Легкий интерфейс, разработанный специально для занятых людей, которым некогда разбираться в множестве кнопок на экране, а требуется просто получить результат имея исходные данные.








