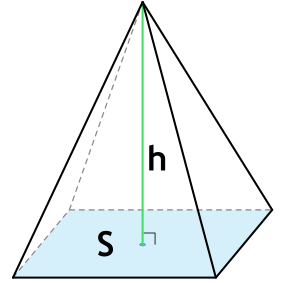
Как найти объем пирамиды с прямоугольным основанием - Сайт, где вы сможете решить свои вопросы

Объем – это количество кубических единиц, которые заполняют пирамиду. Объем прямоугольной пирамиды можно вычислить по формуле: одна третья (×) площадь основания (×) высота пирамиды.

(V=frac{1}{3}S_{осн}h)

Прямоугольная пирамида

Площадь основания:

Высота пирамиды:

Объем правильной пирамиды

Основание правильной пирамиды квадрат.

(V=frac{1}{3}b^2h)

Правильная пирамида

Сторона основания b:

Высота пирамиды:

Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку “Записаться” принимаю условия Пользовательского соглашения и Политики конфиденциальности

Источник

Download Article

To calculate the volume of a pyramid, use the formula $V={frac {1}{3}}lwh$ , where l and w are the length and width of the base, and h is the height. You can also use the equivalent formula $V={frac {1}{3}}A_{{b}}h$ , where $A_{{b}}$ is the area of the base and h is the height. The method varies slightly depending on whether the pyramid has a triangular or a rectangular base. If you want to know how to calculate the volume of a pyramid, just follow these steps.

Volume Help

1

Find the length and width of the base. In this example, the length of the base is 4 cm and the width is 3 cm. If you’re working with a square base, the method is the same, except the length and width of the square base will be equal. Write down these measurements.^[1]
2

Multiply the length and width to find the area of the base. To get the area of the base, simply multiply 3 cm by 4 cm.^[2]²^[3]

Advertisement
3

Multiply the area of the base by the height. The area of the base is 12 cm² and the height is 4 cm, so you can multiply 12 cm² by 4 cm.
4

Multiply your result so far by ${frac {1}{3}}$ . Or, in other words, divide by 3. Remember to state your answer in cubic units whenever you’re working with three-dimensional space.^[4]

1

Find the length and width of the base. The length and width of the base must be perpendicular to each other for this method to work. They can also be considered the base and height of the triangle. In this example, the width of the base is 2 cm and the length of the triangle is 4 cm.^[5]
2

Calculate the area of the base. To calculate the area of the base, just plug the base and height of the triangle into the following formula: $A_{{b}}={frac {1}{2}}bh$ .^[6]
3

Multiply the area of the base by the height of the pyramid. The area of the base is 4 cm² and the height is 5 cm.
4

Multiply your result so far by ${frac {1}{3}}$ . Or, in other words, divide by 3. Your result will show that the volume of a pyramid with a height of 5 cm and a triangular base with a width of 2 cm and a length of 4 cm is 6.67 cm.^[7]³

Add New Question

Question

How do I calculate the volume of a three square tier pyramid?

Determine the area of the base. If it is a rectangle, that’s length x width, if it is a triangle it’s 1/2 x the base (one side) x the height (a line perpendicular to the base to the opposite vertex). Determine the height of the pyramid. It is a line perpendicular (straight up) from the base of the pyramid to the opposite vertex. Muliply (1) x (2) and divide by 3. The formula is 1/3 x the area of the base x the height of the pyramid
Question

How do I find the height if given the volume and the base length for a square pyramid?

Triple the volume and divide that by the area of the base (which is the square of the length of an edge).
Question

How do I double the volume of a square pyramid?

Either double the height of the pyramid or double the area of the base. Accomplish the latter by multiplying the length of each side of the base by the square root of 2 (1.414).

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

This method can be further generalized to such objects as pentagonal pyramids, hexagonal pyramids, etc. The overall process is: A) calculate the area of the base shape; B) measure the height from the tip of the pyramid to the center of the base shape; C) multiply A with B; D) divide by 3.
In a square pyramid, the true height, slant height, and length of the edge of the base face are all related by the Pythagorean theorem: (edge ÷ 2)² + (true height)² = (slant height)²
In all regular pyramids, the slant height, edge height, and edge length are also related by the Pythagorean theorem: (edge ÷ 2)² + (slant height)² = (edge height)²

Thanks for submitting a tip for review!

Pyramids have three kinds of height — a slant height, down the center of the triangular sides; a true height or perpendicular height, that goes from the tip of the pyramid to the center of the base face; and an edge height, that goes down one edge of the triangular sides. For volume, you must use the true height.

References

About This Article

Article SummaryX

To calculate the volume of a pyramid, you need to know its height and the area of the base. Once you have that information, you can find the volume using the formula V (volume) = 1/3 x Ab (the area of the base) x h (height). If the pyramid has a square or rectangular base, simply multiply the width of the base by its length to find the area. Then, multiply the area of the base by the height of the pyramid, and multiply the result by 1/3—which is the same as dividing by 3. For instance, if your pyramid has a square base that is 3 inches long by 3 inches wide, and a height of 4 inches, the volume would be (3 x 3 x 4)/3, or 12. Since you’re describing the volume of a 3-dimensional object, remember to write your answer in cubic units. In this case, the pyramid has a volume of 12 cubic inches. For pyramids with a triangular base, the technique is a little different. If you know the triangle’s height and the width of its base, plug those numbers into the formula ½ x b (base) x h (height) to find the area of the triangle. From there, you can use the same formula that you used for the square-based pyramid. For example, say your pyramid has a base that’s a triangle with a base width of 2 cm and a height of 4 cm, and the pyramid has a height of 6 cm. First, find the area of the triangle using the formula ½ x 2 x 4, which will give you a base area of 4 square centimeters. Next, multiply the area by the height of the pyramid, then multiply the product by 1/3. In this case, 6 x 4 x 1/3 = 8, which means the pyramid has a volume of 8 cubic centimeters. To learn how to calculate the volume of a pyramid with a triangular base, read on!

Did this summary help you?

Thanks to all authors for creating a page that has been read 718,043 times.

Did this article help you?

Источник

Как найти объем прямоугольной пирамиды

Прямоугольной называется пирамида, одно из ребер которой перпендикулярно ее основанию, то есть стоит под углом 90˚. Это ребро является одновременно и высотой прямоугольной пирамиды. Формулу объема пирамиды впервые вывел Архимед.

Вам понадобится

– ручка;
– бумага;
– калькулятор.

Инструкция

В прямоугольной пирамиде высотой будет ее ребро, которое стоит под углом 90˚ к основанию. Как правило, площадь основания прямоугольной пирамиды обозначают как S, а высоту, которая одновременно является ребром пирамиды, − h. Тогда, чтобы найти объем этой пирамиды, необходимо площадь ее основания умножить на высоту и разделить на 3. Таким образом, объем прямоугольной пирамиды вычисляется с помощью формулы: V=(S*h)/3.

Прочитайте условие задачи. Допустим, дана прямоугольная пирамида ABCDES. В ее основании лежит пятиугольник, площадь которого 45 см². Длина высоты SE равна 30 см.

Постройте пирамиду, следуя заданным параметрам. Ее основание обозначьте латинскими буквами ABCDE, а вершину пирамиды – S. Так как чертеж получится на плоскости в проекции, то для того, чтобы не запутаться, обозначьте уже известные вам данные: SE=30см; S(ABCDE)=45 см².

Вычислите объем прямоугольной пирамиды, используя формулу. Подставив данные и сделав подсчеты, получится, что объем прямоугольной пирамиды будет равен: V=(45*30)/3=см³.

Если в условии задачи нет данных о площади основания и высоте пирамиды, то нужно провести дополнительные вычисления для получения этих величин. Площадь основания будет вычисляться в зависимости от того, какой многоугольник лежит в ее основании.

Высоту пирамиды узнаете, если известна гипотенуза любого из прямоугольных треугольников EDS или EAS и угол, под которым наклонена боковая грань SD или SA к ее основанию. Вычислите катет SE по теореме синусов. Он и будет являться высотой прямоугольной пирамиды.

Обратите внимание

Проводя вычисления таких величин, как высота, объем, площадь, следует помнить, что каждая из них имеет свою единицу измерения. Так, площадь измеряется в см², высота – в см, а объем – в см³.
Кубический сантиметр – это единица объема, которая равна объему куба с длиной ребер в 1см. Если подставить данные в нашу формулу, получим: см³= (см²*см)/3.

Полезный совет

Как правило, если в задаче требуется найти объем прямоугольной пирамиды, то все необходимые данные известны – как минимум для того, чтобы найти площадь основания и высоту фигуры.

Источники:

Объем пирамиды

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Загрузить PDF

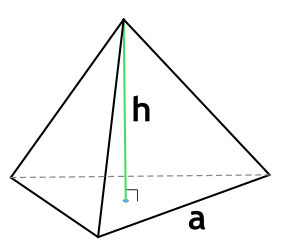
Квадратная пирамида – объемная фигура с основанием в виде квадрата и треугольными боковыми гранями. Вершина квадратной пирамиды проецируется в центр основания. Если «а» – сторона квадратного основания, «h» – высота пирамиды (перпендикуляр, опущенный из вершины пирамиды к центру ее основания), тогда объем квадратной пирамиды можно вычислить по формуле: a² × (1/3)h. Эта формула верна для квадратной пирамиды любых размеров (от сувенирных пирамид до египетских пирамид).

1
Найдите сторону основания. Так как в основании квадратной пирамиды лежит квадрат, то все стороны основания равны. Поэтому необходимо найти длину любой стороны основания.
- Например, дана пирамида, сторона основания которой равна 5 см.
- Если стороны основания не равны друг другу, то вам дана прямоугольная, а не квадратная пирамида. Тем не менее, формула для вычисления объема прямоугольной пирамиды похожа на формулу для вычисления объема квадратной пирамиды. Если «l» и «w» – две смежные (неравные) стороны прямоугольника в основании пирамиды, то объем пирамиды вычисляется по формуле: (l× w) × (1/3)h
2
Вычислите площадь квадратного основания, умножив его сторону саму на себя (или, другими словами, возведя сторону в квадрат).
- В нашем примере: 5 х 5 = 5² = 25 см².
- Не забудьте, что площадь измеряется в квадратных единицах – квадратных сантиметрах, квадратных метрах, квадратных километрах и так далее.
3
Умножьте площадь основания на высоту пирамиды. Высота – перпендикуляр, опущенный из вершины пирамиды на ее основание. Перемножив эти величины, вы получите объем куба с тем же основанием и высотой, как у пирамиды.
- В нашем примере высота равна 9 см: 25 см² × 9 см = 225 см³
- Не забывайте, что объем измеряется в кубических единицах, в данном случае в кубических сантиметрах.
4
Разделите полученный результат на 3 и вы найдете объем квадратной пирамиды.
- В нашем примере: 225 см³ / 3 = 75 см³.
- Объем измеряется в кубических единицах.
Реклама

1
Если вам дана либо площадь, либо высота пирамиды и ее апофема, вы можете найти объем пирамиды, используя теорему Пифагора. Апофема – это высота наклонной треугольной грани пирамиды, проведенная из вершины треугольника к его основанию. Для вычисления апофемы используйте сторону основания пирамиды и ее высоту.
- Апофема делит сторону основания пополам и пересекает ее под прямым углом.
2
Рассмотрите прямоугольный треугольник, образованный апофемой, высотой и отрезком, соединяющим центр основания и середину его стороны. В таком треугольнике апофема является гипотенузой, которую можно найти по теореме Пифагора. Отрезок, соединяющий центр основания и середину его стороны, равен половине стороны основания (этот отрезок является одним из катетов; вторым катетом является высота пирамиды).
- Напомним, что теорема Пифагора записывается так: a² + b² = c², где «a» и «b» – катеты, «c» – гипотенуза прямоугольного треугольника.
- Например, дана пирамида, у которой сторона основания равна 4 см, а апофема – 6 см. Чтобы найти высоту пирамиды, подставьте эти значения в теорему Пифагора.
  - a² + b² = c²
  - a² + (4/2)² = 6²
  - a² = 32
  - a = √32 = 5,66 см Вы нашли второй катет прямоугольного треугольника, который является высотой пирамиды (аналогично, если была бы дана апофема и высота пирамиды, вы бы могли найти половину стороны основания пирамиды).
3
Используйте найденное значение, чтобы найти объем пирамиды по формуле: a² × (1/3)h.
- В нашем примере вы вычислили, что высота пирамиды равна 5,66 см. Подставьте необходимые значения в формулу для вычисления объема пирамиды:
  - a² × (1/3)h
  - 4² × (1/3)(5,66)
  - 16 × 1,89 = 30,24 см³.
4
Если вам не дана апофема, используйте ребро пирамиды. Ребро – это отрезок, соединяющий вершину пирамиды с вершиной квадрата в основании пирамиды. В этом случае вы получите прямоугольный треугольник, катетами которого являются высота пирамиды и половина диагонали квадрата в основании пирамиды, а гипотенузой – ребро пирамиды. Так как диагональ квадрата равна √2 × сторону квадрата, то вы можете найти сторону квадрата (основания), разделив диагональ на √2. Затем вы сможете найти объем пирамиды по вышеописанной формуле.
- Например, дана квадратная пирамида с высотой 5 см и ребром 11 см. Вычислите половину диагонали следующим образом:
  - 5² + b² = 11²
  - b² = 96
  - b = 9,80 см.
  - Вы нашли половину диагонали, поэтому диагональ равна: 9,80 см × 2 = 19,60 см.
  - Сторона квадрата (основания) равна √2 × диагональ, поэтому 19,60 / √2 = 13,90 см. Теперь найдите объем пирамиды по формуле:a² × (1/3)h
  - 13,90² × (1/3)(5)
  - 193,23 × 5/3 = 322,05 см³
Реклама

Советы

В квадратной пирамиде ее высота, апофема и сторона основания связаны теоремой Пифагора: (сторона ÷ 2)² + (высота)² = (апофема)²
В любой правильной пирамиде апофема, сторона основания и ребро связаны теоремой Пифагора: (сторона ÷ 2)² + (апофема)² = (ребро)²

Об этой статье

Эту страницу просматривали 11 758 раз.

Была ли эта статья полезной?

Источник

{V= S cdot h}

На этой странице собраны формулы и калькуляторы для нахождения объема пирамиды. Просто введите известные данные в калькулятор и получите результат. Либо рассчитайте объем пирамиды по приведенным формулам самостоятельно.

Пирамида — многогранник, в основании которого лежит многоугольник, а остальные грани представляют собой треугольники, имеющие общую вершину.

Содержание:

калькулятор объема пирамиды
формула объема пирамиды
объем правильной треугольной пирамиды
объем правильной четырехугольной пирамиды
объем правильной шестиугольной пирамиды
объем правильной n-угольной пирамиды
объем тетраэдра
примеры задач

Формула объема пирамиды

{V= dfrac{1}{3} S cdot h}

S – площадь основания пирамиды

h – высота пирамиды

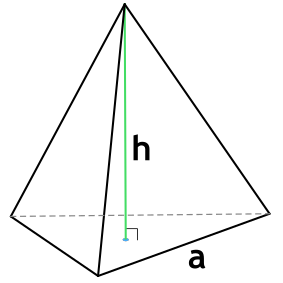
Формула объема правильной треугольной пирамиды

Правильная треугольная пирамида – пирамида, в основании которой лежит равносторонний треугольник, а грани являются равнобедренными треугольниками.

{V= dfrac{h cdot a^2}{4 sqrt{3}}}

a – длина стороны основания пирамиды

h – высота пирамиды

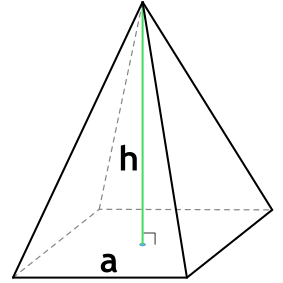
Формула объема правильной четырехугольной пирамиды

Правильная четырехугольная пирамида – пирамида, в основании которой лежит квадрат, а грани являются равнобедренными треугольниками.

{V= dfrac{1}{3} cdot h cdot a^2}

a – длина стороны основания пирамиды

h – высота пирамиды

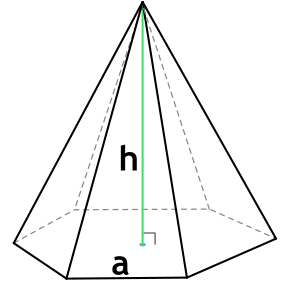
Формула объема правильной шестиугольной пирамиды

Правильная шестиугольная пирамида – пирамида, в основании которой лежит правильный шестиугольник, а грани являются равнобедренными треугольниками.

{V= dfrac{sqrt{3}}{2} cdot h cdot a^2}

a – длина стороны основания пирамиды

h – высота пирамиды

Формула объема правильной n-угольной пирамиды

Правильная пирамида имеет в основании правильный многоугольник (все стороны и углы равны между собой), а высота проходит через центр этого основания.

{V= dfrac{n cdot h cdot a^2}{12 cdot tg(dfrac{180°}{n} )}}

a – длина стороны основания пирамиды

h – высота пирамиды

n – число сторон многоугольника в основании пирамиды

Формула объема тетраэдра

Тетраэдр – правильный многогранник (четырехгранник), имеющий четыре грани, каждая из которых является правильным треугольником. У тетраэдра кроме четырех граней также 4 вершины и 6 ребер.

{V= dfrac{sqrt{2} a^3}{12}}

a – длина стороны тетраэдра

Примеры задач на нахождение объема пирамиды

Задача 1

Найдите объем пирамиды с высотой 2м, а основанием ее служит квадрат со стороной 3м.

Решение

Так как в основании пирамиды лежит квадрат, то воспользуемся формулой объема правильной четырехугольной пирамиды и подставим в нее значения высоты и стороны основания.

V= dfrac{1}{3} cdot h cdot a^2 = dfrac{1}{3} cdot 2 cdot 3^2 = dfrac{1}{3} cdot 2 cdot 9 = dfrac{1}{3} cdot 18 = 6 : м^3

Ответ: 6 м³

Используем калькулятор для проверки полученного ответа.

Задача 2

Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1см, а высота равна √3см.

Решение

Из условия следует, что пирамида правильная треугольная. Это значит, что для решения задачи необходимо воспользоваться формулой для правильной треугольной пирамиды. Подставим в нее значения и рассчитаем объем.

V= dfrac{h cdot a^2}{4 sqrt{3}} = dfrac{sqrt{3} cdot 1^2}{4 sqrt{3}} = dfrac{sqrt{3} cdot 1}{4 sqrt{3}} = dfrac{sqrt{3}}{4 sqrt{3}} = dfrac{cancel{sqrt{3}}}{4 cancel{sqrt{3}}} = dfrac{1}{4} = 0.25 : м^3

Ответ: 0.25 см³

Для проверки с помощью калькулятора извлечем квадратный корень из 3: √3 = 1.73205. Теперь можем подставить значения в калькулятор и проверить полученный ответ.

Источник

Volume Help

References

About This Article

Did this article help you?

Как найти объем прямоугольной пирамиды

Советы

Об этой статье

Была ли эта статья полезной?

Содержание:

Формула объема пирамиды

Формула объема правильной треугольной пирамиды

Формула объема правильной четырехугольной пирамиды

Формула объема правильной шестиугольной пирамиды

Формула объема правильной n-угольной пирамиды

Формула объема тетраэдра

Примеры задач на нахождение объема пирамиды

Вам также может понравиться

Как найти имей в гугл аккаунте

Мышка громко щелкает как исправить

Как составить социальную программу для пожилых

Добавить комментарий Отменить ответ