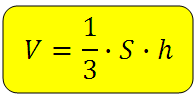{V= S cdot h}
На этой странице собраны формулы и калькуляторы для нахождения объема пирамиды. Просто введите известные данные в калькулятор и получите результат. Либо рассчитайте объем пирамиды по приведенным формулам самостоятельно.
Пирамида — многогранник, в основании которого лежит многоугольник, а остальные грани представляют собой треугольники, имеющие общую вершину.
Содержание:
- калькулятор объема пирамиды
- формула объема пирамиды
- объем правильной треугольной пирамиды
- объем правильной четырехугольной пирамиды
- объем правильной шестиугольной пирамиды
- объем правильной n-угольной пирамиды
- объем тетраэдра
- примеры задач
Формула объема пирамиды
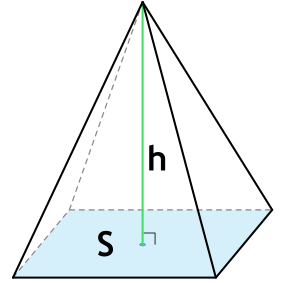
{V= dfrac{1}{3} S cdot h}
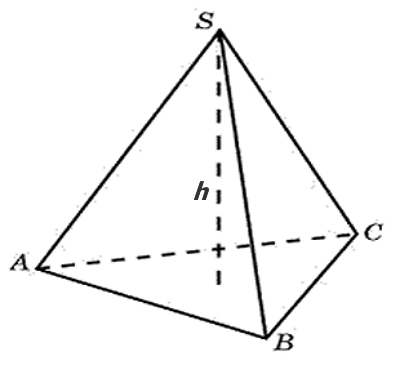
S – площадь основания пирамиды
h – высота пирамиды
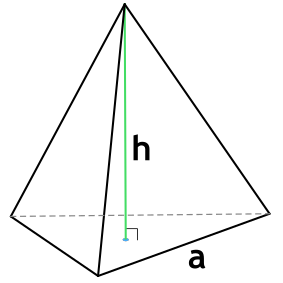
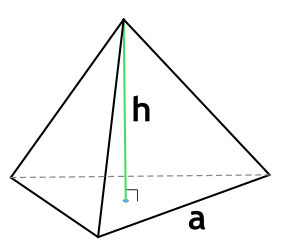
Формула объема правильной треугольной пирамиды
Правильная треугольная пирамида – пирамида, в основании которой лежит равносторонний треугольник, а грани являются равнобедренными треугольниками.
{V= dfrac{h cdot a^2}{4 sqrt{3}}}
a – длина стороны основания пирамиды
h – высота пирамиды
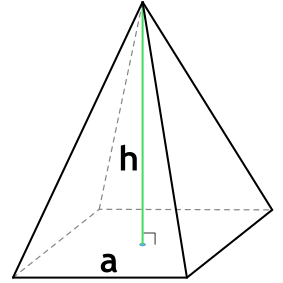
Формула объема правильной четырехугольной пирамиды
Правильная четырехугольная пирамида – пирамида, в основании которой лежит квадрат, а грани являются равнобедренными треугольниками.
{V= dfrac{1}{3} cdot h cdot a^2}
a – длина стороны основания пирамиды
h – высота пирамиды
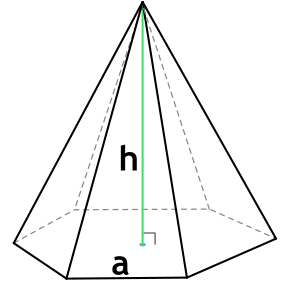
Формула объема правильной шестиугольной пирамиды
Правильная шестиугольная пирамида – пирамида, в основании которой лежит правильный шестиугольник, а грани являются равнобедренными треугольниками.
{V= dfrac{sqrt{3}}{2} cdot h cdot a^2}
a – длина стороны основания пирамиды
h – высота пирамиды
Формула объема правильной n-угольной пирамиды
Правильная пирамида имеет в основании правильный многоугольник (все стороны и углы равны между собой), а высота проходит через центр этого основания.
{V= dfrac{n cdot h cdot a^2}{12 cdot tg(dfrac{180°}{n} )}}
a – длина стороны основания пирамиды
h – высота пирамиды
n – число сторон многоугольника в основании пирамиды
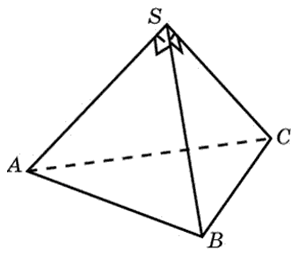
Формула объема тетраэдра
Тетраэдр – правильный многогранник (четырехгранник), имеющий четыре грани, каждая из которых является правильным треугольником. У тетраэдра кроме четырех граней также 4 вершины и 6 ребер.
{V= dfrac{sqrt{2} a^3}{12}}
a – длина стороны тетраэдра
Примеры задач на нахождение объема пирамиды
Задача 1
Найдите объем пирамиды с высотой 2м, а основанием ее служит квадрат со стороной 3м.
Решение
Так как в основании пирамиды лежит квадрат, то воспользуемся формулой объема правильной четырехугольной пирамиды и подставим в нее значения высоты и стороны основания.
V= dfrac{1}{3} cdot h cdot a^2 = dfrac{1}{3} cdot 2 cdot 3^2 = dfrac{1}{3} cdot 2 cdot 9 = dfrac{1}{3} cdot 18 = 6 : м^3
Ответ: 6 м³
Используем калькулятор для проверки полученного ответа.
Задача 2
Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1см, а высота равна √3см.
Решение
Из условия следует, что пирамида правильная треугольная. Это значит, что для решения задачи необходимо воспользоваться формулой для правильной треугольной пирамиды. Подставим в нее значения и рассчитаем объем.
V= dfrac{h cdot a^2}{4 sqrt{3}} = dfrac{sqrt{3} cdot 1^2}{4 sqrt{3}} = dfrac{sqrt{3} cdot 1}{4 sqrt{3}} = dfrac{sqrt{3}}{4 sqrt{3}} = dfrac{cancel{sqrt{3}}}{4 cancel{sqrt{3}}} = dfrac{1}{4} = 0.25 : м^3
Ответ: 0.25 см³
Для проверки с помощью калькулятора извлечем квадратный корень из 3: √3 = 1.73205. Теперь можем подставить значения в калькулятор и проверить полученный ответ.
Пирамида – это многогранник, основанием которого является многоугольник, а грани его являются треугольниками.
Онлайн-калькулятор объема пирамиды
У пирамиды есть ребра. Можно сказать, что они тянутся к точке, называемой вершиной данной пирамиды. Ее основанием может быть произвольный многоугольник. Грань — это фигура, которая образуется в результате объединения двух ближайших ребер со стороной основания. Гранью пирамиды является треугольник. Расстояние от вершины пирамиды до середины стороны основания называется апофемой. Высотой пирамиды называется длина перпендикуляра, опущенного из вершины к центру ее основания.
Типы пирамид
Различают следующие типы пирамид.
- Прямоугольная — у нее ребро образует угол в 90 градусов с основанием.
- Правильная — ее основание — какой-либо правильный многоугольник, а вершина проецируется в центр этого основания.
- Тетраэдр — пирамида, у которой в основании лежит треугольник.
Формулы объема пирамиды
Объем пирамиды находится несколькими способами.
По площади основания и высоте пирамиды
Простое умножение одной трети площади основания на высоту пирамиды и является ее объемом.
V=13⋅Sосн⋅hV=frac{1}{3}cdot S_{text{осн}}cdot h
SоснS_{text{осн}} — площадь основания пирамиды;
hh — высота данной пирамиды.
Площадь основания пирамиды равна 100 см2100text{ см}^2, а высота ее равна 30 см30text{ см}. Найдите объем тела.
Решение
Sосн=100S_{text{осн}}=100
h=30h=30
Все величины нам известны, подставляем их численные значения в формулу и находим:
V=13⋅Sосн⋅h=13⋅100⋅30=1000 см3V=frac{1}{3}cdot S_{text{осн}}cdot h=frac{1}{3}cdot 100cdot 30=1000text{ см}^3
Ответ
1000 см3.1000text{ см}^3.
Формула объема правильной треугольной пирамиды
Этот способ подходит, если пирамида правильная и треугольная.
V=h⋅a243V=frac{hcdot a^2}{4sqrt{3}}
hh — высота пирамиды;
aa — сторона основания пирамиды.
Вычислите объем правильной треугольной пирамиды, если в ее основании лежит равносторонний треугольник, в котором сторона равна 5 см5text{ см}, а высота пирамиды равна – 19 см19text{ см}.
Решение
a=5a=5
h=19h=19
Просто подставляем данные величины в формулу для объема:
V=h⋅a243=19⋅5243≈68.6 см3V=frac{hcdot a^2}{4sqrt{3}}=frac{19cdot 5^2}{4sqrt{3}}approx68.6text{ см}^3
Ответ
68.6 см3.68.6text{ см}^3.
Формула объема правильной четырехугольной пирамиды
V=13⋅h⋅a2V=frac{1}{3}cdot hcdot a^2
hh — высота пирамиды;
aa — сторона основания пирамиды.
Дана правильная четырехугольная пирамида. Вычислите ее объем, если ее высота равна 7 см7text{ см}, a сторона основания составляет – 2 см2text{ см}.
Решение
a=2a=2
h=7h=7
По формуле вычисляем:
V=13⋅h⋅a2=13⋅7⋅22≈9.3 см3V=frac{1}{3}cdot hcdot a^2=frac{1}{3}cdot 7cdot 2^2approx9.3text{ см}^3
Ответ
9.3 см3.9.3text{ см}^3.
Формула объема тетраэдра
V=2⋅a312V=frac{sqrt{2}cdot a^3}{12}
aa — длина ребра тетраэдра.
Длина ребра тетраэдра равна 13 см13text{ см}. Найдите его объем.
Решение
a=13a=13
Подставляем aa в формулу для объема тетраэдра:
V=2⋅a312=2⋅13312≈259 см3V=frac{sqrt{2}cdot a^3}{12}=frac{sqrt{2}cdot 13^3}{12}approx259text{ см}^3
Ответ
259 см3.259text{ см}^3.
Формула объема пирамиды как определитель
Наверное, самый экзотический способ вычисления объема данного тела.
Пусть даны векторы, на которых построена пирамида как на сторонах. Тогда ее объем будет равен одной шестой смешанного произведения векторов. Последний в свою очередь равен определителю составленному из координат этих векторов. Итак, если пирамида построена на трех векторах:
a⃗=(ax,ay,az)vec{a}=(a_x, a_y, a_z)
b⃗=(bx,by,bz)vec{b}=(b_x, b_y, b_z)
c⃗=(cx,cy,cz)vec{c}=(c_x, c_y, c_z),
тогда объем соответствующей пирамиды это такой определитель:
V=16⋅∣axayazbxbybzcxcycz∣V=frac{1}{6}cdotbegin{vmatrix}
a_x & a_y & a_z \
b_x & b_y & b_z \
c_x & c_y & c_z \
end{vmatrix}
Найти объем пирамиды через смешанное произведение векторов, координаты которых такие: a⃗=(2,3,5)vec{a}=(2,3,5) , b⃗=(1,4,4)vec{b}=(1,4,4), c⃗=(3,5,7)vec{c}=(3,5,7).
Решение
a⃗=(2,3,5)vec{a}=(2,3,5)
b⃗=(1,4,4)vec{b}=(1,4,4)
c⃗=(3,5,7)vec{c}=(3,5,7)
По формуле:
V=16⋅∣235144357∣=16⋅(2⋅4⋅7+3⋅4⋅3+5⋅1⋅5−5⋅4⋅3−2⋅4⋅5−3⋅1⋅7)=16⋅(56+36+25−60−40−21)=16⋅(−4)=−23≈−0.7V=frac{1}{6}cdotbegin{vmatrix}
2 & 3 & 5 \
1 & 4 & 4 \
3 & 5 & 7 \
end{vmatrix}=frac{1}{6}cdot(2cdot4cdot7 + 3cdot4cdot3 + 5cdot1cdot5 – 5cdot4cdot3 – 2cdot4cdot5 – 3cdot1cdot7) =frac{1}{6}cdot( 56 + 36 + 25 – 60 – 40 – 21)=frac{1}{6}cdot(-4)=-frac{2}{3}approx-0.7
Мы должны взять модуль этого числа, так как объем это неотрицательная величина:
V=0.7 см3V=0.7text{ см}^3
Ответ
0.7 см3.0.7text{ см}^3.
Не знаете, где можно оформить заказ контрольных работ недорого? Наши эксперты помогут вам с решением работ по объемам фигур!
Тест по теме “Объем пирамиды”
В данной публикации мы рассмотрим, как можно найти объем пирамиды и разберем примеры решения задач для закрепления материала.
-
Формула вычисления объема пирамиды
-
1. Общая формула
- 2. Объем правильной треугольной пирамиды
- 3. Объем правильной четырехугольной пирамиды
- 4. Объем правильной шестиугольной пирамиды
-
1. Общая формула
- Примеры задач
Формула вычисления объема пирамиды
1. Общая формула
Объем (V) пирамиды равняется одной третьей произведения ее высоты на площадь основания.
- ABCD – основание;
- E – вершина;
- h – высота, перпендикулярная основанию.
2. Объем правильной треугольной пирамиды
Основанием правильной треугольной пирамиды является равносторонний треугольник (ABC), площадь которого вычисляется так (а – сторона треугольника):
Подставляем данное выражение в формулу расчета объема фигуры и получаем:
3. Объем правильной четырехугольной пирамиды
Основанием правильной четырехугольной пирамиды является квадрат, площадь которого считается так: S = a2, где а – длина его стороны.
Следовательно, формулу объема можно представить в виде:
4. Объем правильной шестиугольной пирамиды
Основанием правильной шестиугольной пирамиды является правильный шестиугольник, площадь которого вычисляется по формуле (а – сторона основания):
С учетом этого, объем фигуры считается так:
Примеры задач
Задание 1
Найдите объем правильной треугольной пирамиды, если известно, что ее высота составляет 16 см, а длина стороны ее основания – 8 см.
Решение:
Воспользуемся соответствующей формулой, подставив в нее известные значения:
Задание 2
Высота правильной четырехугольной пирамиды равна 12 см, а сторона ее основания – 3 см. Найдите объем фигуры.
Решение:
Площадь квадрата, который является основанием пирамиды, равна 9 см2 (3 см ⋅ 3 см). Следовательно, объем равен:
Объём правильной пирамиды. Продолжаем рассматривать задачи с пирамидами. На блоге уже рассмотрены задания с правильными пирамидами, в этих статьях шла речь о нахождении элементов и площади поверхности. Здесь разберём примеры связанные с понятием объёма. Для решения подобных заданий обязательно нужно знать формулу объёма пирамиды:
S – площадь основания пирамиды
h – высота пирамиды
Основанием может быть любой многоугольник. Но в большинстве задач на ЕГЭ речь в условии, как правило, идёт о правильных пирамидах. Напомню одно из её свойств:
Вершина правильной пирамиды проецируется в центр её основания
Посмотрите на проекцию правильной треугольной, четырёхугольной и шестиугольной пирамид (ВИД СВЕРХУ):
Можете посмотреть ещё одну статью на блоге, где разбирались задачи связанные с нахождением объёма пирамиды. Рассмотрим задачи:
27087. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна корню из трёх.
Объём пирамиды вычисляется по формуле:
S – площадь основания пирамиды
h – высота пирамиды
Найдём площадь основания пирамиды, это правильный треугольник. Воспользуемся формулой – площадь треугольника равна половине произведения соседних сторон на синус угла между ними, значит:
Таким образом, объём пирамиды равен:
Ответ: 0,25
27088. Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен корню из трёх.
Такие понятия как высота пирамиды и характеристики её основания связаны формулой объёма:
S – площадь основания пирамиды
h – высота пирамиды
Сам объём нам известен, площадь основания можем найти, так как известны стороны треугольника, который является основанием. Зная указанные величины без труда найдём высоту.
Для нахождения площади основания воспользуемся формулой – площадь треугольника равна половине произведения соседних сторон на синус угла между ними, значит:
Таким образом, подставив данные значения в формулу объема можем вычислить высоту пирамиды:
Высота равна трём.
Ответ: 3
27109. В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.
Объём пирамиды вычисляется по формуле:
S – площадь основания пирамиды
h – высота пирамиды
Высота нам известна. Необходимо найти площадь основания. Напомню, что вершина правильной пирамиды проецируется в центр её основания. Основанием правильной четырёхугольной пирамиды является квадрат. Мы можем найти его диагональ. Рассмотрим прямоугольный треугольник (выделен синим):
Отрезок соединяющий центр квадрата с точкой В это катет, который равен половине диагонали квадрата. Этот катет можем вычислить по теореме Пифагора:
Значит BD = 16. Вычислим площадь квадрата воспользовавшись формулой площади четырёхугольника:
Следовательно:
Таким образом, объём пирамиды равен:
Ответ: 256
27178. В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.
Высота пирамиды и её и объём известны, значит можем найти площадь квадрата, который является основанием. Зная площадь квадрата, мы сможем найти его диагональ. Далее рассмотрев прямоугольный треугольник по теореме Пифагора вычислим боковое ребро:
Найдём площадь квадрата (основания пирамиды):
Вычислим диагональ квадрата. Так как его площадь равна 50, то сторона будет равна корню из пятидесяти и по теореме Пифагора:
Точка О делит диагональ BD пополам, значит катет прямоугольного треугольника ОВ = 5.
Таким образом, можем вычислить чему равно боковое ребро пирамиды:
Ответ: 13
245353. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3.
Как уже неоднократно было сказано – объём пирамиды вычисляется по формуле:
S – площадь основания пирамиды
h – высота пирамиды
Боковое ребро перпендикулярное основанию равно трём, это означает, что высота пирамиды равна трём. Основания пирамиды – это многоугольник, площадь которого равна:
Таким образом:
Ответ: 27
27086. Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.
Посмотреть решение
27110. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 600. Высота пирамиды равна 6. Найдите объем пирамиды.
Посмотреть решение
27111. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.
Посмотреть решение
27113. Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 1. Найдите объем шестиугольной пирамиды.
Посмотреть решение
27114. Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.
Посмотреть решение
27176. Найдите объем пирамиды, высота которой равна 6, а основание — прямоугольник со сторонами 3 и 4.
Посмотреть решение
27179. Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.
Посмотреть решение
27181. Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 450. Найдите объем пирамиды.
Посмотреть решение
На этом всё. Успеха Вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Как рассчитать объем пирамиды
На данной странице калькулятор поможет рассчитать объем пирамиды онлайн. Для расчета задайте площадь, высоту, сторону или количество сторон. Вычисления производятся в миллиметрах, сантиметрах, метрах. Результат выводится в кубических сантиметрах, литрах и кубических метров.
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. Пирамида является частным случаем конуса. Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания.
Пирамида
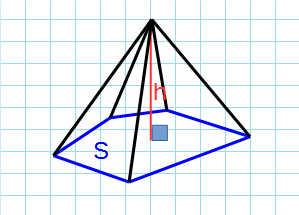
Формула объема пирамиды через высоту и площадь основания:
S – площадь основания; h – высота пирамиды.
Правильная пирамида
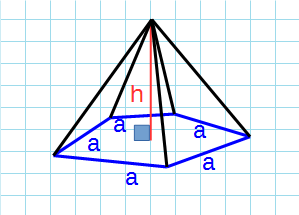
Правильная пирамида — пирамида, в основании которой лежит правильный многоугольник, а высота проходит через центр основания.
Формула объема правильной пирамиды через сторону основания, высоту и количество сторон:
a – сторона основания; h – высота пирамиды; n – количество сторон многогранника в основании.
Правильная треугольная пирамида
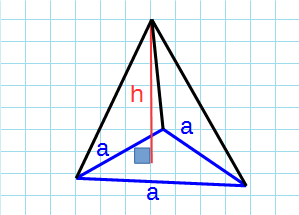
Правильная треугольная пирамида — пирамида, у которой основанием является равносторонний треугольник и грани равные равнобедренные треугольники.
Формула объема правильной треугольной пирамиды через сторону основания и высоту:
a – сторона основания; h – высота пирамиды.
Правильная четырехугольная пирамида
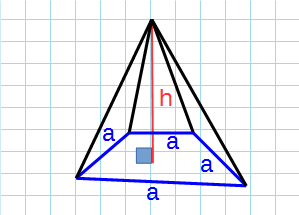
Правильная четырехугольная пирамида — пирамида, у которой основанием является квадрат и грани равные равнобедренные треугольники.
Формула объема правильной четырехугольной пирамиды через сторону основания и высоту:
a – сторона основания; h – высота пирамиды.
Тетраэдр
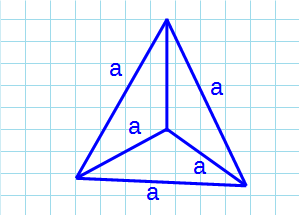
Тетраэдр — пирамида, у которой все грани равносторонние треугольники.
Формула объема тетраэдра:
a – ребро тетраэдра.