Как определить объём цилиндра при его погружении в воду?
Анонимный вопрос
2 декабря 2018 · 12,0 K
Инженер по профессии, люблю спорт, музыку, кино. · 2 дек 2018
Согласно закону Архимеда, объем тела, погруженного в воду равен объему вытесненной им воды.
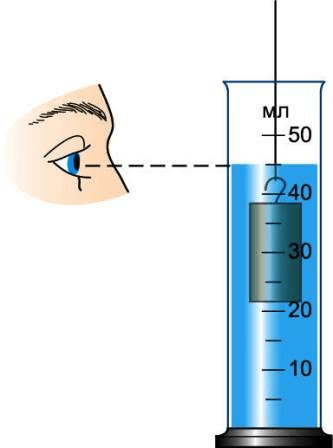
Чтобы определить таким образом объем цилиндра, нужно взять мерный стакан с водой со шкалой объема. Определить по шкале первоначальный объем воды – V1.
Затем погружаем цилиндр в воду и отмечаем объем воды после погружения – V2.
Тогда объем цилиндра бует равен разности конечного и начального объемов воды:
V = V2 – V1.
11,7 K
Комментировать ответ…Комментировать…
Цель работы:
Научиться определять объём тела с помощью измерительного цилиндра.
Приборы и материалы:
Измерительный цилиндр (мензурка), тела неправильной формы небольшого объёма (гайки, фарфоровые ролики, кусочки металла и др.), нитки.
Указания к работе:
1. Определите цену деления мензурки.
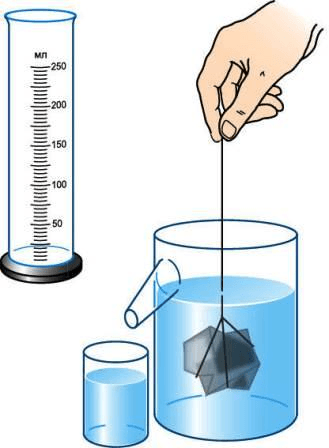
2. Налейте в мензурки столько воды, чтобы тело можно было полностью погрузить в воду, и измерьте её объём.
3. Опустите тело, объём которого надо измерить, в воду, удерживая его за нитку (рис. 201), и снова измерьте объём жидкости.
4. Проделайте опыты, описанные в пунктах 2 и 3, с некоторыми другими имеющимися у вас телами.
5. Результаты измерений запишите в таблицу 9.
Дополнительное задание.
Если тело неправильной формы не входить в мензурку, то его объём можно определить с помощью отливного сосуда (рис. 202). Перед измерением сосуд наполняют водой до отверстия отливной трубки. При погружении в него тела часть воды, равная объёму тела, выливается. Измерив мензуркой её объём, определяют объём погружённого в жидкость тела.
Таблица 9.
рис. 201
рис. 202
reshalka.com
ГДЗ учебник по физике 7 класс Перышкин. №4 Измерение объема тела. Номер №1
Решение
Объём тела неправильной формы точно измерить с помощью измерительных приборов нельзя. Поэтому для измерения объема воспользуемся мензуркой. Тело, полностью погружённое в жидкость, вытесняет объём жидкости, который равен объёму самого тела. Воспользуемся этим законом и найдем объёмы некоторых тел следующим образом. Нальем достаточное количество воды в мензурку, а затем погрузим полностью туда наше тело. Разница между первоначальным объёмом и объёмом жидкости, в которое погружено тело, равна объёму этого тела.
V
=
V
2
−
V
1
, где
V
2
− объём воды и тела,
V
1
− начальный объём воды в мензурке.
- Прежде чем проводить измерения физической величины с помощью измерительного прибора нужно определите цену деления его шкалы.
Для определения цены деления необходимо взять 2 соседних числа, найти их разницу (от большего отнять меньшее), а затем разделить полученное число на количество маленьких штрихов между этими числами.
На шкале цилиндра возьмём, к примеру, числа 20 и 30.
Таким образом, цена каждого деления будет равна
30
−
202
=
10
2= 5 мл. - В мензурку нальём столько воды, чтобы тело можно было полностью погрузить в воду. Начальный объём воды равен 70
с
м
3
. - Опустим тело, объём которого надо измерить (шарик, брусок, цилиндр), в воду, удерживая его за нитку, и снова измерим объём жидкости.
Вычисления.
V
б
р
=
95
−
70
=
25с
м
3
V
ц
=
85
−
65
=
20с
м
3
V
ш
=
75
−
60
=
15с
м
3
- Результаты измерений запишем в таблицу 9.
Таблица 9.
| № опыта | Название тела | Начальный объём воды в мензурке
V 1 , с м 3 |
Объём воды и тела
V 2 , с м 3 |
Объём тела V,
с м 3 V = V 2 − 1 |
|---|---|---|---|---|
| 1 | Брусок | 70 | 95 | 25 |
| 2 | Цилиндр | 65 | 85 | 20 |
| 3 | Шарик | 60 | 75 | 15 |
Вывод. В ходе лабораторной работы мы научились измерять объёмы тел с помощью измерительного цилиндра и выяснили, что объём тел равен разнице объёма воды, в которое погружено тело, и первоначального объёма воды.
Нахождение погруженного в жидкость объема тела через силу Архимеда
Задача обратная задаче расчета силы Архимеда, по известной силе Архимеда найти объем тела.
Задача обратная задаче расчета силы Архимеда см. Сила Архимеда, по известной силе Архимеда найти объем тела, погруженный в воду.
Поскольку сила Архимеда нам известна и соответствует она объему вытесненной жидкости — то есть, той части объема тела, которая погрузилась в воду, — калькулятор получается в одно действие:
Нахождение объема тела через силу Архимеда
Ускорение св. падения, м/с2
Ускорение свободного падения, м/с2
Точность вычисления
Знаков после запятой: 6
Ссылка скопирована в буфер обмена
Похожие калькуляторы
- • Сила Архимеда
- • Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.
- • Закон Ома
- • Закон Кулона
- • Давление на поверхность
- • Раздел: Физика ( 52 калькуляторов )
PLANETCALC, Нахождение погруженного в жидкость объема тела через силу Архимеда
Timur2020-11-03 14:19:33
Объем погруженной части тела равен объему вытесненной жидкости.
Сила Архимеда: FA = ρgV, где
ρ — плотность жидкости/газа, [кг/м3];
g — ускорение свободного падения, [м/с2];
V — объем погруженной части тела, [м3].
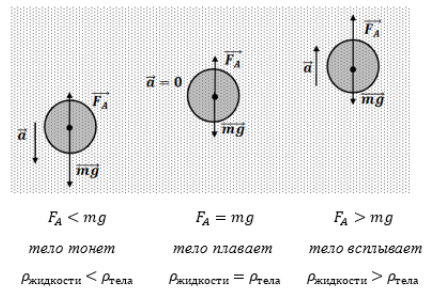
Условия плавания тел:
Если тело плавает в равновесии (полностью или частично погружено в воду), то сила Архимеда уравновешивает силу тяжести.
FA=mg.
Объем погруженной части тела:
$V_{text{погруж}} = V_{text{тела}}frac{rho_{text{тела}}}{rho_{text{жидкости}}}$ ,
где V погруж — объем погруженной части тела, [м3];
V тела — объем тела, [м3];
ρ жидкости — плотность жидкости, [кг/м3];
ρ тела — плотность тела, [кг/м3]
Тело плавает в жидкости при условии, что сила Архимеда равна силе тяжести:
FА=Fтяж.
.
Чтобы найти архимедову (выталкивающую) силу, действующую на тело в жидкости, надо плотность жидкости умножить на ускорение свободного падения ((g=9,8) Н/кг) и на объём погружённой в жидкость части тела:
Силу тяжести вычислим по формуле:
Fтяж.=m⋅g=ρтела⋅Vвсего тела⏟∥m⋅g
Подставив соответствующие значения в первую формулу, получим:
ρж⋅g⋅Vчасти тела=ρтела⋅Vвсего тела⋅gρж⋅Vчасти тела=ρтела⋅Vвсего тела⇒Vчасти телаVвсего тела=ρтелаρж
Отношение объёма погружённой части тела к полному объёму тела равно отношению плотности тела к плотности жидкости.
.
На иллюстрации бревно наполовину погружено в воду, потому что его плотность меньше плотности воды в (2) раза.
Айсберг состоит из льда. Его плотность на (10) (%) меньше плотности воды.
Это означает, что часть айсберга, которая находится под водой, в (9) раз больше части айсберга, находящейся над водой. По этой причине айсберги опасны для судов.