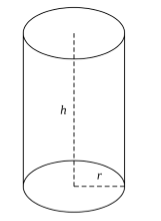
Как найти объем полной поверхности цилиндра

Как найти объем полной поверхности цилиндра

4.png

Рис. (1). Цилиндр

Площадь поверхности цилиндра состоит из площади боковой поверхности и площади оснований цилиндра.

Площадь боковой поверхности цилиндра

где (R) — радиус цилиндра,

(H) — высота цилиндра

р 7.png

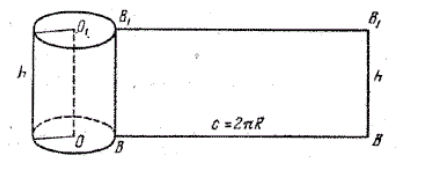
Рис. (2). Боковая поверхность цилиндра

Развёртка боковой поверхности цилиндра на плоскости — прямоугольник.

Одна сторона прямоугольника является  высотой цилиндра.

(AB = H).

Вторая сторона прямоугольника является длиной окружности основания цилиндра.

Основания цилиндра — круги.  (S(круга) =)

πR2

.

Площадь полной поверхности цилиндра равна:

(S(полн.) = 2S(осн.) + S(бок.) =)

2πR2

 (+)

2πRH

.

Объём цилиндра (V)(цилиндра) (=)

πR2
·H

.

Источники:

Рис. 1. Цилиндр, © ЯКласс.
Рис. 2. Боковая поверхность цилиндра, © ЯКласс. 

Источник

Напомним,
что цилиндр – это тело, полученное при вращении прямоугольника вокруг
прямой, проходящей через одну из его сторон.

Назовём
элементы цилиндра.

Основания
цилиндра – два равных круга радиуса .

Отрезок,
соединяющий окружности оснований и перпендикулярный основаниям, называется образующей
цилиндра и обозначается .
Все образующие цилиндра параллельны и равны.

Осью
цилиндра
называется прямая, проходящая через центры оснований. Она параллельна образующим.

Высота
цилиндра  –
перпендикуляр, опущенный из любой точки одного основания на другое, или другими
словами, это расстояние между плоскостями оснований цилиндра. Образующая
цилиндра равна его высоте.

Радиусом
цилиндра называется радиус его основания.

Цилиндр
называется равносторонним, если его высота равна диаметру основания.

Осевым
сечением цилиндра называется сечение цилиндра плоскостью,
проходящей через его ось. Осевое сечение цилиндра – прямоугольник, две
стороны которого есть образующие цилиндра, а две другие – диаметры его
оснований.

Сечение,
параллельное оси цилиндра, является прямоугольником.

Сечение,
перпендикулярное оси цилиндра, является кругом, равным основаниям цилиндра.

Боковая
поверхность цилиндра может быть развёрнута в
прямоугольник со сторонами, одна из которых равна длине окружности основания,
другая – высоте цилиндра.

Площадь
боковой поверхности цилиндра можно вычислить по следующим
формулам:

,
,
,

где
 –
длина окружности основания,  –
высота цилиндра,  –
радиус основания,  –
образующая.

Площадь
полной поверхности цилиндра равна сумме площади боковой
поверхности цилиндра и двух площадей его оснований.

Тогда
площадь полной поверхности цилиндра можно вычислить по формуле:

,

где
 –
радиус оснований цилиндра,  –
его высота.

Объём цилиндра
равен произведению площади основания на высоту.

Тогда
его можно вычислить по формуле:

,

где
 –
радиус оснований цилиндра,  –
его высота.

Основные
моменты мы с вами повторили, а теперь давайте перейдём к практической части
занятия.

Задача
первая. Радиус основания цилиндра равен  см,
высота цилиндра равна диаметру его основания. Найдите площадь боковой
поверхности цилиндра.

Решение.

Задача
вторая. Найдите площадь сечения цилиндра плоскостью, параллельной
его оси и проходящей на расстоянии  см
от неё, если площадь полной поверхности цилиндра равна  см2,
а площадь боковой поверхности  см2.

Решение.

Задача
третья. Призма со сторонами основания  см
и  см
и диагональю  см
вписана в цилиндр. Найдите объём и площадь полной поверхности цилиндра.

Решение.

Задача
четвёртая. Плоскость, параллельная оси цилиндра, отсекает от
окружности основания дугу .
Диагональ полученного сечения равна  и
удалена от оси цилиндра на расстояние .
Найдите объём цилиндра.

Решение.

Задача
пятая. В цилиндрический сосуд налили  см3
воды. Уровень жидкости оказался равным  см.
В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся
на  см.
Найдите, чему равен объём детали. Ответ выразите в см3.

Решение.

Источник

Здание Планетария Тихо Браге, Копенгаген, его крыша является примером цилиндрического сечения

Цили́ндр (др.-греч. κύλινδρος — валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

Связанные определения[править | править код]

  • Цилиндрическая поверхность — поверхность, образуемая однопараметрическим семейством параллельных прямых (называемых образующими) и проходящими через точки некоторой кривой (называемой направляющей).
  • Плоские фигуры, образованные пересечением цилиндрической поверхности с двумя параллельными плоскостями, ограничивающими цилиндр, называются основаниями этого цилиндра.
  • Часть цилиндрической поверхности, находящаяся между плоскостями оснований, называется боковой поверхностью цилиндра.
  • Высотой цилиндра называется отрезок, высекаемый плоскостями его оснований на прямой, перпендикулярной им, или длина этого отрезка.

Типы цилиндров[править | править код]

  • Прямым называется цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), прямая между которыми перпендикулярна плоскостям этих оснований. Данная прямая называется осью цилиндра.
  • Косым называется цилиндр, основания которого имеют центры симметрии (например, являются кругами или эллипсами), отрезок между которыми не перпендикулярен плоскостям этих оснований.
  • Круговым называется цилиндр с окружностью в роли направляющей.
  • Цилиндром вращения, или прямым круговым цилиндром (часто под цилиндром подразумевают именно его) называется цилиндр, который можно получить вращением (то есть тело вращения) прямоугольника вокруг одной из его сторон, содержащая которую прямая в таком случае будет осью этого цилиндра и его осью симметрии.
  • Цилиндр, основания которого являются эллипсами, параболами или гиперболами, называют соответственно эллиптическим, параболическим и гиперболическим; последние два имеют бесконечный объём.
  • Призма также является разновидностью цилиндра — с основанием в виде многоугольника.
  • Равносторонним называется цилиндр вращения, диаметр основания которого равен его высоте[1].

Свойства[править | править код]

  • Если плоскость основания цилиндра параллельна плоскости направляющей, то граница этого основания будет по форме совпадать с направляющей кривой.

Площадь поверхности цилиндра[править | править код]

Площадь боковой поверхности[править | править код]

К вычислению площади боковой поверхности цилиндра

Площадь боковой поверхности цилиндра равна длине образующей, умноженной на периметр сечения цилиндра плоскостью, перпендикулярной образующей.

Площадь боковой поверхности прямого цилиндра вычисляется по его развёртке. Развёртка цилиндра представляет собой прямоугольник с высотой h и длиной P, равной периметру основания. Следовательно, площадь боковой поверхности цилиндра равна площади его развёртки и вычисляется по формуле:

S_{b}=Ph

В частности, для прямого кругового цилиндра:

P=2pi R, и S_{b}=2pi Rh, здесь и далее R — радиус основания цилиндра.

Для наклонного цилиндра площадь боковой поверхности равна длине образующей, умноженной на периметр сечения, перпендикулярного образующей:

S_{b}=P_{perp }h

Простой формулы, выражающей площадь боковой поверхности косого цилиндра через параметры основания и высоту, в отличие от объёма не существует. Для наклонного кругового цилиндра можно воспользоваться приближёнными формулами для периметра эллипса, а затем умножить полученное значение на длину образующей.

Площадь полной поверхности[править | править код]

Площадь полной поверхности цилиндра равна сумме площадей его боковой поверхности и его оснований.

Для прямого кругового цилиндра:
S_{p}=2pi Rh+2pi R^{2}=2pi R(h+R)

Объём цилиндра[править | править код]

Для наклонного цилиндра существуют две формулы:

  • Объём равен длине образующей, умноженной на площадь сечения цилиндра плоскостью, перпендикулярной образующей.
    V=S_{perp }l,
  • Объём равен площади основания, умноженной на высоту (расстояние между плоскостями, в которых лежат основания):
    V=Sh=Slsin {varphi },
где l — длина образующей, а varphi  — угол между образующей и плоскостью основания. Для прямого цилиндра h=l.

Для прямого цилиндра sin {varphi }=1, l=h и S_{perp }=S, и объём равен:

  • V=Sl=Sh

Для кругового цилиндра:

V=pi R^{2}h=pi {frac {d^{2}}{4}}h,

где d — диаметр основания.

Примечания[править | править код]

  1. ↑ Математический справочник
Источник

Цилиндр

Автор статьи

Сергей Евгеньевич Грамотинский

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Понятие цилиндра

Определение 1

Геометрическая фигура, образованная двумя равными кругами, лежащими в параллельных плоскостях, все точки которых соединены между параллельными прямыми, так что никакая точка не остается несоединенной, называется цилиндром (рис. 1).

Цилиндр

Рисунок 1. Цилиндр

Круги при этом называются основаниями цилиндра, а прямые их соединяющие — образующими. Прямая, которая проходит через центры окружностей оснований называется осью цилиндра, а совокупность всех образующих — боковой поверхностью цилиндра.

Виды цилиндров

Определение 2

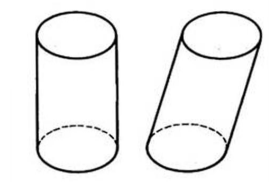
Цилиндр, у которого все образующие перпендикулярны к плоскостям, проходящим через основания, называется прямым. В противном же случае он является наклонным (рис. 2).

Прямой и наклонный цилиндры

Рисунок 2. Прямой и наклонный цилиндры

Логотип baranka

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Площадь поверхности цилиндра

Площадь поверхности цилиндра определяется следующим образом:

Найдем теперь формулы для вычисления площадь боковой поверхности и основания.

Так как в основании лежат круги, то очевидно, что

Площадь боковой поверхности цилиндра определяется как произведение длины окружности, ограничивающей основание цилиндра на его высоту.

Доказательство.

Для доказательства этой теоремы нам необходимо найти площадь развертки боковой поверхности цилиндра (рис. 3).

Рисунок 3.

Видим, что разверткой боковой поверхности цилиндра является прямоугольник. Высота прямоугольника равняется высоте цилиндра $h$, а длина равняется длине окружности, ограничивающей основание цилиндра, то есть

«Цилиндр» 👇

Теорема доказана.

Объем цилиндра

Теорема 2

Объем цилиндра определяется как произведение площади основания цилиндра на его высоту.

Доказательство.

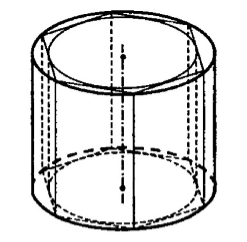
Рассмотрим цилиндр с радиусом $r$ и высотой $h$. Найдем ее объем $V$. Для этого сначала впишем в нее правильную $n-$угольную призму, в которую впишем еще один цилиндр. Пусть радиус второго цилиндра равняется $r’$, а её объем равен $V’$ (рис. 4).

Рисунок 4.

Как мы знаем, объем призмы будет равен $S_{осн.пр.}h$. Следовательно, получим следующую оценку

Тогда из оценки, получим

Теорема доказана.

Пример задачи

Пример 1

Найти площадь полной поверхности цилиндра и его объем, если радиус его основания равняется $7$ см, а высота в два раза больше диаметра основания.

Решение.

Найдем вначале высоту цилиндра. Так как высота в два раза больше диаметра, получим

[h=2cdot 2r=4r=28 см]

Как мы знаем

[S_{осн}=pi r^2=49pi ]

По теореме 1

[S_{бок}=2pi rh=392pi ]

Тогда

[S_{полн}=S_{бок}+2S_{осн}=392pi +98pi =490pi ]

По теореме 2

[V=pi r^2h=49pi cdot 28=1372pi ]

Ответ: $490pi , 1372pi $

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 19.04.2023

Источник

Как посчитать объем цилиндра

  1. Главная
  2. /
  3. Математика
  4. /
  5. Геометрия
  6. /
  7. Как посчитать объем цилиндра

Чтобы посчитать объем цилиндра воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

цилиндр

Найти чему равен объем цилиндра (V) можно зная (либо-либо):

  • радиус r и высоту h цилиндра
  • диаметр d и высоту h цилиндра
  • площадь основания So и высоту h цилиндра
  • площадь боковой поверхности Sb и высоту h цилиндра

Подставьте значения в соответствующие поля и получите результат.

Зная радиус r и высоту h

Чему равен объем цилиндра если его радиус

r = ,

а высота

h = ?

Ответ: V =

0

Чему равен объем цилиндра V если известны его радиус r и высота h?

Формула

V = π⋅r2⋅h

Пример

Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:

V = 3.14156 ⋅ 22 ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см3

Зная диаметр d и высоту h

Чему равен объем цилиндра если его диаметр

d = ,

а высота

h = ?

Ответ: V =

0

Чему равен объем цилиндра V если известны его диаметр d и высота h?

Формула

V = π⋅(d/2)2⋅h

Пример

Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:

V = 3.14156 ⋅ (1/2)2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см3

Зная площадь основания So и высоту h

Чему равен объем цилиндра если площадь его основания

So = ,

а высота

h = ?

Ответ: V =

0

Чему равен объем цилиндра V если известны его площадь основания So и высота h?

Формула

V = So⋅h

Пример

Если цилиндр имеет высоту h = 10 см, а площадь его основания So = 5 см2, то:

V = 10 ⋅ 5 = 50 см3

Зная площадь боковой поверхности Sb и высоту h

Чему равен объем цилиндра если площадь его боковой поверхности

Sb = ,

а высота

h = ?

Ответ: V =

0

Чему равен объем цилиндра V если известны его площадь боковой поверхности Sb и высота h?

Формула

V = Sb2/4πh

Пример

Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности Sb = 30 см2, то:

V = 302/ 4 ⋅ 3.14⋅ 5 = 900/62.8 = 14.33 см3

См. также

Источник

Добавить комментарий