Как найти объем полной поверхности тела вращения

Как найти объем полной поверхности тела вращения

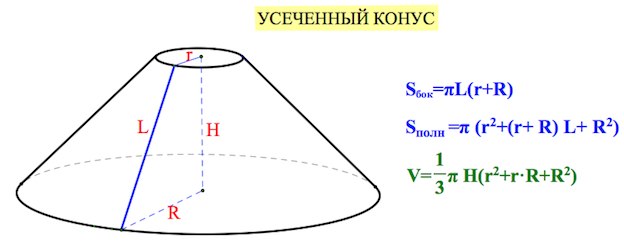
Тела и поверхности вращения. Шар. Цилиндр. Конус

Тела и поверхности вращения.

Шар. Цилиндр. Конус. Площади поверхности и объемы этих фигур.

Подробная теория с наглядными иллюстрациями и основные формулы.

Читай эту статью, здесь все это есть.

Всего за 15 минут ты полностью во всём разберешься!

Тело вращения – это тело в пространстве, которое возникает при вращении какой-нибудь плоской фигуры вокруг какой-нибудь оси.

Вот самый простой пример: цилиндр.

Берем прямоугольник и начинаем вращать его вокруг одной из сторон.

Смотри.

Было–вращаем–стало:

А теперь гораздо хитрее. Бывает так, что ось вращения находится далеко от фигуры, которая вращается.

Например, так:

Вращаем:

Что получится? Бублик. А по-научному – ТОР.

Ну и так вот можно любую фигуру вертеть вокруг любой оси, и будут получаться разные более или менее сложные тела вращения.

Ну, а поверхность вращения – это просто граница тела вращения. Ведь поверхность это всегда граница тела.

Здесь мы рассмотрим подробно несколько тел вращения. Те, которые встречаются в школьных задачах. Это шар, цилиндр и конус.

Шар

Шар – тело вращения, полученное вращением полуокружности вокруг диаметра.

Было–вращаем–стало:

Вообще-то есть и другое определение шара – через ГМТ (геометрическое место точек)

Шар – геометрическое место точек, удаленных от одной фиксированной точки на расстояние, не более заданного.

Скажу тебе по секрету, что, хоть второе определение и пугающее на вид, оно удобнее в обращении. Задумайся, ведь если тебя попросят сказать, что такое шар, ты скажешь что-то вроде:

«ну …там есть центр и радиус…», подразумевая, что все точки внутри шара находятся я на расстоянии не большем, чем радиус.

Ну, в общем, шар он и есть шар.

Названия, которые ты должен знать:

Незнакомое тебе, наверное, только одно.

Диаметральное сечение шара – сечение, проходящее через центр. Это сечение иногда еще называют большим кругом.

А вообще:

  • Любое сечение шара – круг.
  • Граница шара называется сфера. (Так же, как граница круга – окружность.)

Площадь поверхности сферы

( {{S}_{поверхности }}=4pi {{R}^{2}})

( R) – радиус

Откуда взялось? Умные математики придумали – это не так уж просто – придется просто запомнить.

Объем шара

( {{V}_{шара}}=frac{4}{3}pi {{R}^{3}})

( R) – радиус

Это еще одна хитрая формула, которую придется запомнить, не понимая, откуда она взялась.

Если ты знаком с производной, то можешь заметить это:

( {{V’}_{шара}}={{S}_{поверхности}})

И это не случайно! Но почему это так вышло, мы тоже здесь обсуждать не будем. Можешь попробовать доказать это сам!

Цилиндр

Цилиндр – тело, образованное вращением прямоугольника вокруг одной из сторон.

Вообще-то, полное имя этого тела – «прямой круговой цилиндр», но составители задач и мы вместе с ними по дружбе называем его просто цилиндром. Названия, относящиеся к цилиндру, такие:

Основания у цилиндра – это круги

Еще у цилиндра есть так называемая развертка.

Представь, что у нас от цилиндра осталась только боковая поверхность, и мы ее разрезали вдоль образующей и развернули.

Что получится? Представь себе, прямоугольник.

Развертка цилиндра – прямоугольник.

Площадь боковой поверхности цилиндра

( {{S}_{бок.}}=2pi RH)

( R) – радиус

( H) – высота, она же образующая.

Откуда взялась эта формула? Это как раз легко! Именно потому, что цилиндр можно развернуть, и получится прямоугольник ( 2pi Rcdot H).

Площадь этого прямоугольника и есть площадь боковой поверхности цилиндра. 

Площадь прямоугольника, как мы хорошо помним равна произведению сторон, поэтому

( {{S}_{бок.}}=2pi RH)

Площадь полной поверхности цилиндра

Прибавляем теперь площадь двух кругов – оснований и получаем:

( {{S}_{полн .}}=2pi RH+2pi {{R}^{2}})

Можно вынести (хотя и не обязательно) ( 2pi R):

( {{S}_{полн .}}=2pi Rleft( H+R right))

Но эту формулу неудобно запоминать!

Гораздо проще запомнить, что полная поверхность – сумма боковой поверхности и еще двух кругов – оснований, а боковая поверхность – прямоугольник. И тогда ( {{S}_{полн .}}) можно вообще не запоминать, ты всегда сам напишешь, что

( {{S}_{полн .}}=underbrace{2pi RH}_{прямоугольник}+underbrace{2pi {{R}^{2}}}_{два круга})

Объем цилиндра

( V=pi {{R}^{2}}H)

( R) – радиус основания ( H) – высота

Это точно как у призмы и параллелепипеда!

( V={{S}_{основания}}cdot H), только у призмы и параллелепипеда ( {{S}_{основания}}) — это площадь многоугольника, а у цилиндра ( {{S}_{основания}}) — это площадь круга.

Конус

Конус – тело вращения, образованное вращением прямоугольного треугольника вокруг одного из катетов.

Было–вращаем–стало:

И опять же, полное название этого тела: «прямой круговой конус», но во всех задачах у нас говорится просто «конус».

Названия, относящиеся к конусу:

Что тут нужно твердо помнить?

  • Основание корпуса – круг
  • Все образующие конуса – равны.

Ясно ли это? Вроде должно быть ясно, ведь образующая – это гипотенуза (одна и та же!) Треугольника, который вращаем, а радиус основания – катет.

У конуса тоже есть развертка.

Снова представим, что основания нет, разрежем боковую поверхность вдоль образующей и развернём кулек. Что получится?

Представь себе сектор круга. Пусть длина образующей равна ( l).

Развертка конуса – сектор круга радиуса ( l)

Площадь поверхности конуса

Как найти площадь боковой поверхности корпуса? Вспомним о развертке, ведь для цилиндра все было просто именно с помощью развертки.

По формуле площади сектора ( {{S}_{бок.}}={{l}^{2}}cdot frac{alpha }{2}) Где ( alpha ) – угол при вершине в радианах.

И это уже формула. В некоторых задачах бывает дан именно угол при вершине в развертке конуса.

Но если все же даны только образующая и радиус основания, как быть?

Нужно осознать, что же такое дуга в развертке? Это бывшая окружность основания! Поэтому длина этой дуги равна ( 2pi R).

С другой стороны, длина этой же дуги равна ( alpha cdot l), так как это дуга окружности радиуса ( l). Поэтому

( alpha cdot l=2pi R)

Подставляем

( {{S}_{бок.}}={{l}^{2}}cdot frac{alpha }{2}=frac{l}{2}cdot alpha cdot l=frac{l}{2}cdot 2pi R)

Итак,

( {{S}_{бок.}}=pi Rl), где

( R) — радиус окружности основания,

( l) — длина образующей

Ну, и осталось площадь полной поверхности конуса. Прибавим к боковой поверхности площадь круга основания, и получаем:

( {{S}_{полн. }}=pi Rl+pi {{R}^{2}})

Можно вынести ( pi R):

( {{S}_{полн. }}=pi Rleft( l+R right))

Но, как и для цилиндра, не надо запоминать вторую формулу, гораздо проще всегда пользоваться первой.

Объём конуса

( V=frac{1}{3}pi {{R}^{2}}H)

( R) – радиус основания (

H) – высота

Это так же, как у пирамиды

( V=frac{1}{3}{{S}_{осн.}}cdot H), только

( {{S}_{осн. }}) — это не площадь многоугольника, а площадь круга.

А вот откуда взялась ( frac{1}{3})?, по-прежнему остается загадкой, потому что эта ( frac{1}{3}) получена в результате довольно хитрых рассуждений умных математиков.

А тебе нужно очень твердо запомнить, что в формулах объёма «треугольных» фигур: конуса и пирамиды эта ( frac{1}{3}) и есть, а в формулах параллелепипеда, призмы и цилиндра ее нет!

Бонус: Вебинары по стереометрии из нашего курса подготовки к ЕГЭ по математике

ЕГЭ 14 Стереометрия. Расстояние между точками и от точки до прямой

В этом видео мы научимся «видеть» 3-мерное пространство и изображать 3-мерные объекты на бумаге (то есть на плоской поверхности).

Затем мы научимся двум основным вещам — находить расстояние между точками на таких рисунках, а также расстояние от точки до прямой.

На этих умениях строится всё дальнейшее изучение стереометрии. В общем это очень важное, базовое видео, с которого нужно начинать изучение стереометрии.

Не перескакивайте, не пропускайте его! Даже если вы знаете стереометрию, вы найдете для себя очень много полезного и нового в этом видео.

ЕГЭ 14. Стереометрия. Пирамида. Разбор варианта профильного ЕГЭ 2020

В этом видео:

  • Как нарисовать шестиугольную пирамиду.
  • Как подписать вершины пирамиды чтобы потом легче было решать задачу.
  • Как исправить рисунок, если грани пирамиды сливаются.
  • Доказательство пунктов А и Б, а также их правильная запись, которую примет любой проверяющий на ЕГЭ.
  • Нахождение площади основания и объема пирамиды.
  • Самое главное, на что нужно обратить внимание.

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Алексей Шевчук — ведущий мини-групп

математика, информатика, физика

+7 (905) 541-39-06 — WhatsApp/Телеграм для записи

alexei.shevchuk@youclever.org — email для записи

  • тысячи учеников, поступивших в лучшие ВУЗы страны
  • автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
  • закончил МФТИ, преподавал на малом физтехе;
  • репетиторский стаж — c 2003 года;
  • в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
  • отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».

Источник

07
Май 2013

Категория: Справочные материалыСтереометрия

Тела вращения. Формулы объема и площади поверхности

Елена Репина
2013-05-07
2021-07-02

объем конуса, объем цилиндра, объем шара, площадь поверхности конуса, площадь поверхности цилиндра, площадь поверхности сферы

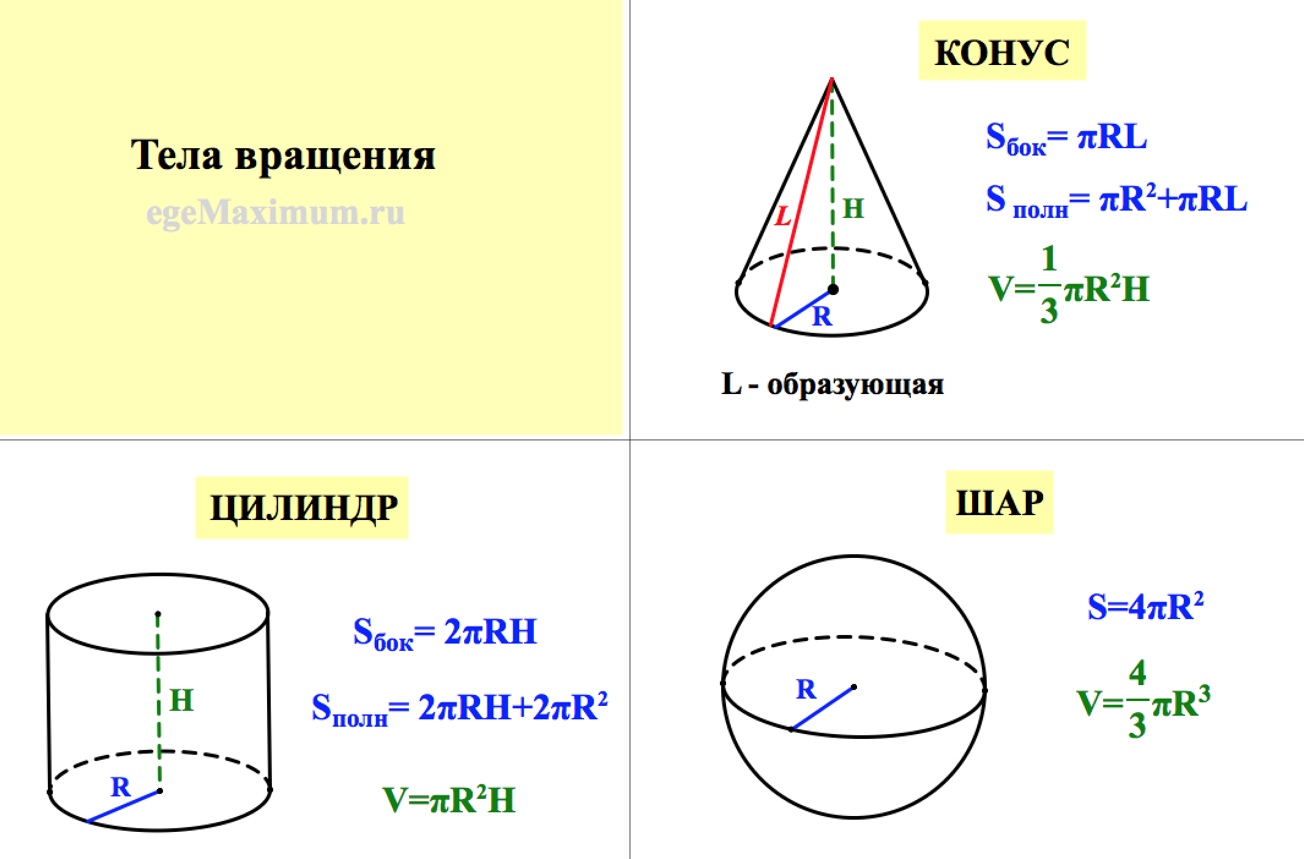
В частности,

усеченный конус

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Печать страницы

комментариев 6

  1. Анатолий

    2014-02-18 в 13:07

    Есть вероятность что на ЕГЭ понадобятся формулы усечённого конуса?

    [ Ответить ]

    • egeMax

      2014-02-18 в 13:18

      C2. Но можно же и самому их получить!.. Я бы не стала заучивать…

      [ Ответить ]

      • Анатолий

        2014-02-18 в 13:36

        в таком случае, напишите в статье как это сделать 🙂

        [ Ответить ]

        • egeMax

          2014-02-18 в 13:57

          Постараюсь сделать позже… Объем усеченного конуса – разность объемов исходного и отсеченного. Тот же принцип с площадью бок.поверхности. Это было бы хорошей задачей для самостоятельной работы 😉

          [ Ответить ]

          • Анатолий

            2014-02-18 в 14:03

            ладно ладно… 🙂

            [ Ответить ]

          • egeMax

            2014-02-18 в 14:09

            😀

            [ Ответить ]

Добавить комментарий

  • Материалы для подготовки к ЕГЭ

  •    

  • Рубрики
    • 01 Геометрия (12)
    • 02 Стереометрия (9)
    • 03 Теория вероятностей ч.1 (1)
    • 04 Теория вероятностей ч.2 (1)
    • 05 Простейшие уравнения (5)
    • 06 Вычисления (5)
    • 07 Производная, ПО (4)
    • 08 «Прикладные» задачи (5)
    • 09 Текстовые задачи (7)
    • 10 Графики функций (7)
    • 11 Исследование функции (2)
    • 12 (С1) Уравнения (79)
    • 13 (С2) Стереометр. задачи (95)
    • 14 (С3) Неравенства (90)
    • 15 (С4) Практич. задачи (72)
    • 16 (С5) Планиметр. задачи (87)
    • 17 (С6) Параметры* (80)
    • 18 (С7) Числа, их свойства (39)
    • A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
    • A2 Читаем графики (нет в ЕГЭ-22) (1)
    • Видеоуроки (44)
    • ГИА (11)
      • II часть (11)
    • ЕГЭ (диагностич. работы) (70)
    • Задачи (24)
    • Иррациональные выражения, уравнения и неравенства (15)
    • Логарифмы (39)
    • МГУ (12)
    • Метод интервалов (4)
    • Метод рационализации (18)
    • Модуль (9)
    • Параметр (40)
    • Переменка (5)
    • Планиметрия (59)
    • Показательные выражения, уравнения и неравенства (8)
    • Разложение на множители (1)
    • Рациональные выражения, уравнения и неравенства (10)
    • Справочные материалы (92)
    • Стереометрия (52)
    • Т/P A. Ларина (443)
    • Текстовые задачи (12)
    • Теория чисел (2)
    • Тесты по темам (80)
    • Тригонометрические выражения, уравнения и неравенства (43)
    • Функции и графики (10)
  • Дружественные сайты

    Сайт А. Ларина
    ЕгэТренер – О. Себедаш
    Математика?Легко!
    Егэ? Ок! – И. Фельдман

  • Свежие записи
    • Задания 18 ЕГЭ 2023
    • Задания 17 ЕГЭ 2023
  • Архивы Архивы

Источник

Образование поверхности вращения

Тела вращения — объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости[1].

Примеры тел вращения[править | править код]

  • Шар — образован полукругом, вращающимся вокруг диаметра разреза
  • Цилиндр — образован прямоугольником, вращающимся вокруг одной из сторон

За площадь боковой поверхности цилиндра принимается площадь его развёртки:

{displaystyle S_{bok}=2pi rh}.
  • Конус — образован прямоугольным треугольником, вращающимся вокруг одного из катетов

За площадь боковой поверхности конуса принимается площадь его развертки:

{displaystyle S_{bok}=pi rl}.

Площадь полной поверхности конуса:

{displaystyle S_{poln}=pi r(r+l)}.
  • Тор — образован окружностью, вращающейся вокруг прямой, не пересекающей его[2]

При вращении контуров фигур возникает поверхность вращения (например, сфера, образованная окружностью), в то время как при вращении заполненных контуров возникают тела (как шар, образованный кругом).

Объём тел вращения[править | править код]

Вращение вокруг оси x[править | править код]

Integral apl rot objem1.svg

Объём тела, образуемого вращением вокруг оси x фигуры, ограниченной графиком функции y=f(x) на интервале [a;b], осью x и прямыми x=a и x=b, равен:

{displaystyle V_{x}=pi int _{a}^{b}f^{2}(x)dx}

Вращение вокруг оси y[править | править код]

Integral apl rot objem2.svg

Объём тела, образуемого вращением вокруг оси y фигуры, ограниченной графиком функции y=f(x) на интервале [a;b], осью x и прямыми x=a и x=b, равен:

{displaystyle V_{y}=2pi int _{a}^{b}xf(x)dx}

Теорема Гульдина[править | править код]

Объём и площадь поверхности тел вращения можно также узнать при помощи теорем Гульдина-Паппа, которые связывают площадь или объём с центром масс фигуры.

  • Первая теорема Гульдина-Паппа гласит:

Площадь поверхности, образуемой при вращении линии, лежащей в плоскости целиком по одну сторону от оси вращения, равна произведению длины линии на длину окружности, пробегаемой центром масс этой линии.

  • Вторая теорема Гульдина-Паппа гласит:

Объём тела, образуемого при вращении фигуры, лежащей в плоскости целиком по одну сторону от оси вращения, равен произведению площади фигуры на длину окружности, пробегаемой центром масс этой фигуры.

Литература[править | править код]

А. В. Погорелов. «Геометрия. 10-11 класс» § 21.Тела вращения. — 2011

Примечания[править | править код]

  1. ↑ А. В. Погорелов. §21. Тела вращения // Геометрия. 10-11 класс. — 2011.
  2. ↑ Математика. Энциклопедия для детей том 11й ISBN 5-94623-072-7

Ссылки[править | править код]

Источник

Объем тела вращения и площадь поверхности тела вращения

Автор статьи

оксана николаевна кузнецова

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Задача 1

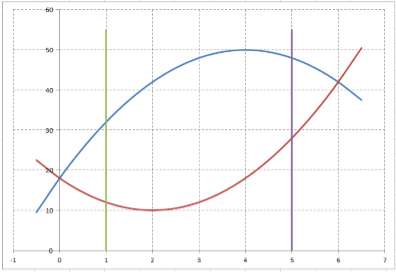
Найти объем тела, образованного вращением (ОТВ) вокруг оси $Ox$ плоской фигуры, ограниченной сверху параболой $y_{1} =-2cdot x^{2} +16cdot x+18$, снизу — параболой $y_{2} =2cdot x^{2} -8cdot x+18$, а слева и справа прямыми $x=1$ и $x=5$ соответственно.

Выполняем графические построения:

Объем <a href=тела вращения и площадь поверхности тела вращения”>

При вращении этой плоской фигуры вокруг оси $Ox$ верхняя парабола (обозначенная синим цветом) образует общий объем, а нижняя парабола (обозначенная оранжевым цветом) образует отверстие. Таким образом, ОТВ вычисляется как разность общего объема и объема отверстия.

Известно, что ОТВ (вокруг оси $Ox$) вычисляется по формуле $V=pi cdot int limits _{a}^{b}y^{2} left(xright)cdot dx $, где $y=yleft(xright)$ — неотрицательная непрерывная функция, образующая криволинейную трапецию на отрезке $left[a,; bright]$.

Общий объем будем вычислять по формуле $V_{1} =pi cdot int limits _{1}^{5}y_{1}^{2} cdot dx $.

Получаем:

[V_{1} =pi cdot int limits _{1}^{5}left(-2cdot x^{2} +16cdot x+18right)^{2} cdot dx =]

[=pi cdot int limits _{1}^{5}left(left(-2cdot x^{2} right)^{2} +left(16cdot xright)^{2} +left(18right)^{2} +2cdot left(-2cdot x^{2} right)cdot left(16cdot xright)+right. ]

[left. +2cdot left(-2cdot x^{2} right)cdot 18+2cdot left(16cdot xright)cdot 18right)cdot dx=]

[=pi cdot int limits _{1}^{5}left(4cdot x^{4} -64cdot x^{3} +184cdot x^{2} +576cdot x+324right)cdot dx =]

[=pi cdot left(4cdot int limits _{1}^{5}x^{4} cdot dx -64cdot int limits _{1}^{5}x^{3} cdot dx +184cdot int limits _{1}^{5}x^{2} cdot dx +576cdot int limits _{1}^{5}xcdot dx +324cdot int limits _{1}^{5}dx right)=]

[=pi cdot left(4cdot left[frac{x^{5} }{5} right]_{1}^{5} -64cdot left[frac{x^{4} }{4} right]_{1}^{5} +184cdot left[frac{x^{3} }{3} right]_{1}^{5} +576cdot left[frac{x^{2} }{2} right]_{1}^{5} +324cdot left[xright]_{1}^{5} right)=]

[=pi cdot left(4cdot frac{1}{5} cdot left(5^{5} -1^{5} right)-64cdot frac{1}{4} cdot left(5^{4} -1^{4} right)+184cdot frac{1}{3} cdot left(5^{3} -1^{3} right)+right. ]

[left. +576cdot frac{1}{2} cdot left(5^{2} -1^{2} right)+324cdot left(5-1right)right)=]

[=pi cdot left(4cdot frac{1}{5} cdot 3124-64cdot frac{1}{4} cdot 624+184cdot frac{1}{3} cdot 124+576cdot frac{1}{2} cdot 24+324cdot 4right)=]

[=pi cdot left(2499,2-9984+7605,3+6912+1296right)=pi cdot 8328,5approx 26151,5.]

Аналогичным образом находим объем отверстия:

[V_{2} =pi cdot int limits _{1}^{5}y_{2} ^{2} cdot dx =pi cdot int limits _{1}^{5}left(2cdot x^{2} -8cdot x+18right)^{2} cdot dx .]

Теперь вычисляем объем тела: $V=V_{1} -V_{2} $.

Задача 2

Вычислить ОТВ, образованного вращением вокруг оси $Ox$ фигуры, ограниченной линиями $y=x^{4} $ и $y=x$.

Графическое изображение фигуры:

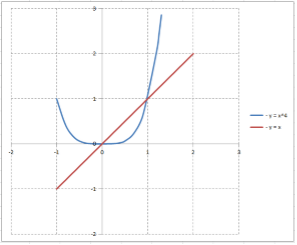
Объем тела вращения и площадь поверхности тела вращения

Решив совместно уравнения $y=x^{4} $ и $y=x$, получим $x_{1} =0$ и $x_{2} =1$ — этими прямыми фигура ограничена слева и справа.

Искомый объем определяется как разность объемов, полученных в результате вращения вокруг оси $Ox$ двух криволинейных трапеций: первая ограничена прямой $y_{1} =x$, вторая — параболой $y_{2} =x^{4} $.

ОТВ, образованного вращением вокруг оси $Ox$ криволинейной трапеции, ограниченной сверху кривой $y=y_{1} left(xright)$, снизу — кривой $y=y_{2} left(xright)$, а также двумя прямыми $x=a$ и $x=b$ слева и справа, будем вычислять по формуле $V=pi cdot int limits _{a}^{b}left(y_{1}^{2} -y_{2}^{2} right)cdot dx $.

Имеем:

[V=pi cdot int limits _{0}^{1}left(left(xright)^{2} -left(x^{4} right)^{2} right)cdot dx =pi cdot left[frac{x^{3} }{3} -frac{x^{9} }{9} right]_{0}^{1} =pi cdot left(frac{1}{3} -frac{1}{9} right)=pi cdot frac{2}{9} .]

«Объем тела вращения и площадь поверхности тела вращения» 👇

Задача 3

Зайти площадь поверхности, образованной вращением вокруг оси $Ox$ кривої $y=sqrt{80cdot x+15} $ между точками з абсцисами $x=3$ и $x=13$.

Графическое изображение вращаемой кривой:

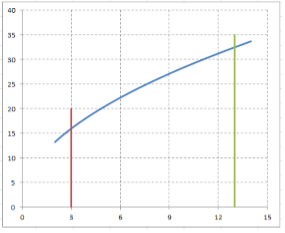
Объем тела вращения и площадь поверхности тела вращения

Площадь поверхности тела вращения выражается формулой $Q=2cdot pi cdot int limits _{a}^{b}ycdot sqrt{1+y’^{2} } cdot dx $, где $y=yleft(xright)$ — неотрицательная функция, заданная на отрезке $left[a,; bright]$.

Находим выражение $sqrt{1+y’^{2} } $:

[y’=frac{80}{2cdot sqrt{80cdot x+15} } ;]

[sqrt{1+y’^{2} } =sqrt{1+frac{80^{2} }{4cdot left(80cdot x+15right)} } =frac{1}{2} cdot sqrt{frac{320cdot x+6460}{80cdot x+15} } .]

Находим выражение для подынтегральной функции $ycdot sqrt{1+y’^{2} } $:

[sqrt{80cdot x+15} cdot frac{1}{2} cdot sqrt{frac{320cdot x+6460}{80cdot x+15} } =frac{1}{2} cdot sqrt{320cdot x+6460} .]

Записываем интеграл и вычисляем площадь поверхности:

[Q=pi cdot int limits _{3}^{13}sqrt{320cdot x+6460} cdot dx =]

[=pi cdot left[frac{1}{320} cdot frac{left(320cdot x+6460right)^{frac{1}{2} +1} }{frac{1}{2} +1} right]_{3}^{13} =pi cdot left[frac{1}{480} cdot left(320cdot x+6460right)^{frac{3}{2} } right]_{3}^{13} =]

[=frac{pi }{480} cdot left[left(320cdot x+6460right)cdot sqrt{320cdot x+6460} right]_{3}^{13} =]

[=frac{pi }{480} cdot left(left(320cdot 13+6460right)cdot sqrt{320cdot 13+6460} -right. ]

[left. -left(320cdot 3+6460right)cdot sqrt{320cdot 3+6460} right)=]

[=frac{pi }{480} cdot left(10620cdot sqrt{10620} -7420cdot sqrt{7420} right)approx ]

[approx frac{3,14}{480} cdot left(10620cdot 103,053-7420cdot 86,139right)approx ]

$approx frac{3,14}{480} cdot left(1094423-639151right)approx frac{3,14}{480} cdot 455272approx 2978$ кв.од.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 19.01.2023

Источник

Определение
3. Тело
вращения – это тело, полученное вращением
плоской фигуры вокруг оси, не
пересекающей фигуру и лежащей с ней в
одной плоскости.

Ось вращения может
и пересекать фигуру, если это ось
симметрии фигуры.

Теорема
2. Пусть
криволинейная трапеция, ограниченная
графиком непрерывной неотрицательной
функции
,
осьюи отрезками прямыхивращается вокруг оси.
Тогда объём получающегося тела вращения
можно вычислить по формуле


(2)

Доказательство.
Для такого тела сечение с абсциссой
– это круг радиуса,
значити формула (1) даёт требуемый результат.

Если фигура
ограничена графиками двух непрерывных
функций
и,
и отрезками прямыхи,
причёми,
то при вращении вокруг оси абсцисс
получим тело, объём которого

Пример
3. Вычислить
объём тора, полученного вращением круга,
ограниченного окружностью вокруг оси абсцисс.

Решение.
Указанный круг снизу ограничен графиком
функции
,
а сверху –.
Разность квадратов этих функций:

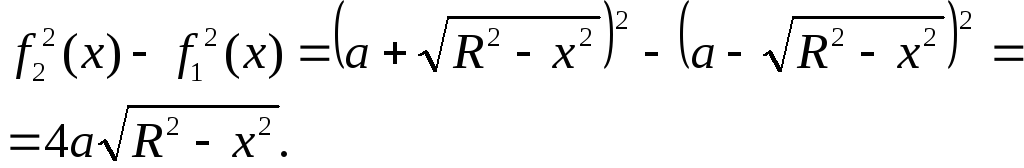
Искомый объём

(графиком
подынтегральной функции является
верхняя полуокружность, поэтому
написанный выше интеграл – это площадь
полукруга).

Пример 4.
Параболический сегмент с основанием
,
и высотой,
вращается вокруг основания. Вычислить
объём получающегося тела («лимон»
Кавальери).

Р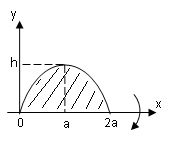ешение.
Параболу расположим как показано на
рисунке. Тогда её уравнение
,
причем.
Найдём значение параметра:.
Итак, искомый объём:

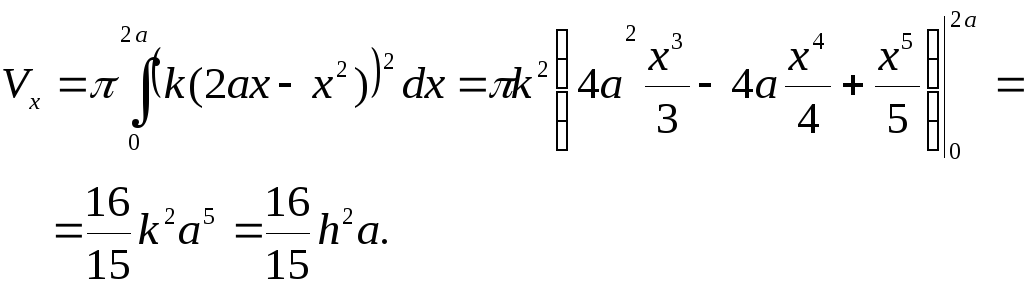
Теорема
3. Пусть
криволинейная трапеция, ограниченная
графиком непрерывной неотрицательной
функции
,
осьюи отрезками прямыхи,
причём,
вращается вокруг оси.
Тогда объём получающегося тела вращения
может быть найден по формуле

(3)

Идея
доказательства.
Разбиваем отрезок
точками,
на части и проводим прямые.
Вся трапеция разложится на полоски,
которые можно считать приближенно
прямоугольниками с основаниеми высотой.

Получающийся при
вращении такого прямоугольника цилиндр
разрежем по образующей и развернём.
Получим «почти» параллелепипед с
размерами:
,и.
Его объём.
Итак, для объёма тела вращения будем
иметь приближенноё равенство

Для получения
точного равенства надо перейти к пределу
при .
Написанная выше сумма есть интегральная
сумма для функции ,
следовательно, в пределе получим интеграл
из формулы (3). Теорема доказана.

Замечание
1. В теоремах
2 и 3 условие
можно опустить: формула (2) вообще
нечувствительна к знаку,
а в формуле (3) достаточнозаменить на.

Пример
5.
Параболический сегмент (основание
,
высота)
вращается вокруг высоты. Найти объём
получающегося тела.

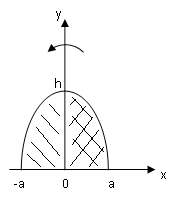Решение.
 Расположим
параболу как показано на рисунке. И хотя
ось вращения пересекает фигуру, она –
ось – является осью симметрии. Поэтому
надо рассматривать лишь правую половину
сегмента. Уравнение параболы
,
причем,
значит.
Имеем для объёма:

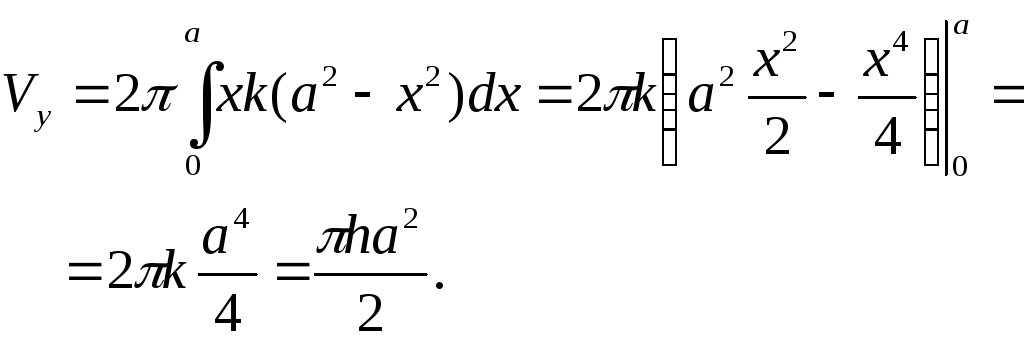
Замечание
2. Если
криволинейная граница криволинейной
трапеции задана параметрическими
уравнениями
,,и,то можно использовать формулы (2) и (3) с
заменойнаинапри измененииt
от
до.

Пример
6. Фигура
ограничена первой аркой циклоиды
,,,
и осью абсцисс. Найти объём тела,
полученного вращением этой фигуры
вокруг: 1) оси;
2) оси.

Решение.
1) Общая формула
В нашем случае:

2) Общая формула
Для нашей фигуры:

Предлагаем
студентам самостоятельно провести все
вычисления.

Замечание
3. Пусть
криволинейный сектор, ограниченный
непре-рывной линией
и лучами,,
вращается вокруг полярной оси. Объём
получающегося тела можно вычислить по
формуле.

Пример
7. Часть
фигуры, ограниченной кардиоидой
,
лежащая вне окружности,
вращается вокруг полярной оси. Найти
объём тела, которое при этом получается.

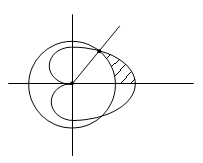Решение.
Обе линии, а значит и фигура, которую
они ограничивают, симметричны относительно
полярной оси. Поэтому необходимо
рассматривать лишь ту часть, для которой

.
Кривые пересекаются прии

при
.
Далее, фигуру можно рассматривать как
разность двух секторов, а значит и объём
вычислять как разность двух интегралов.
Имеем:

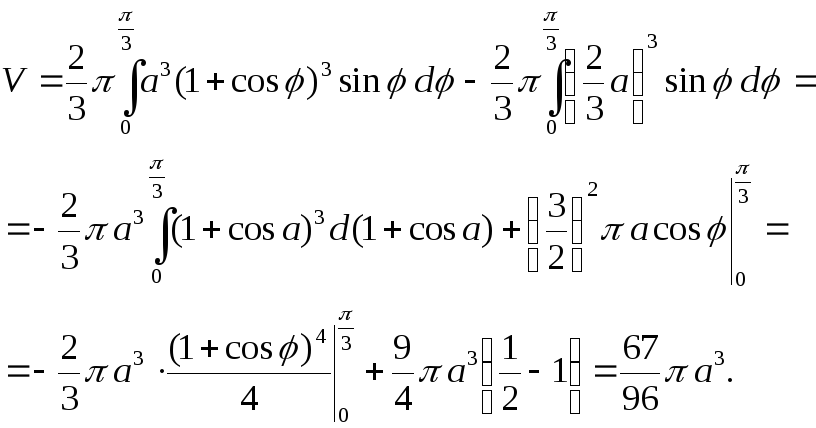
Задачи
для самостоятельного решения.

1. Круговой сегмент,
основание которого ,
высота
,
вращается вокруг основания. Найти объём
тела вращения.

2. Найти объём
параболоида вращения, основание которого
,
а высота равна.

3. Фигура, ограниченная
астроидой
,вращает-ся вокруг оси абсцисс. Найти
объём тела, которое получается при этом.

4. Фигура, ограниченная
линиями
ивращается вокруг оси абсцисс. Найти
объём тела вращения.

Соседние файлы в папке Лекции по мат.анализу

  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Добавить комментарий