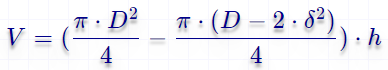Как найти объем полости цилиндра

Как найти объем полости цилиндра

Объём стенки цилиндра

  1. Главная
  2. /
  3. Математика
  4. /
  5. Геометрия
  6. /
  7. Объём стенки цилиндра

Чтобы посчитать объём стенки цилиндра, то есть объём полого цилиндра, воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Полый цилиндр

Найти чему равен объём полого цилиндра (Vст) можно зная (либо-либо):

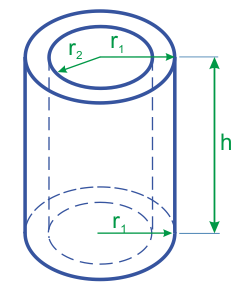
  • Высоту цилиндра h, внешний радиус r1 и внутренний радиус r2
  • Высоту цилиндра h, внешний диаметр d1 и внутренний диаметр d2
  • Высоту цилиндра h, внешний радиус r1 и толщину стенки δ
  • Высоту цилиндра h, внутренний радиус r2 и толщину стенки δ
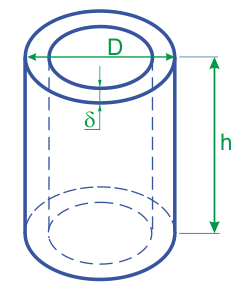
  • Высоту цилиндра h, внешний диаметр d1 и толщину стенки δ
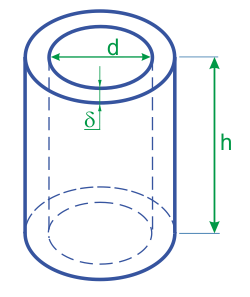
  • Высоту цилиндра h, внутренний диаметр d2 и толщину стенки δ

Зная оба радиуса (диаметра)

Чему равен объём стенки цилиндра Vст если:

Внешний =
Внутренний =
Высота цилиндра h =

Ответ: Vст =

0

Зная толщину стенки

Чему равен объём стенки цилиндра Vст если:

=
Толщина стенки δ =
Высота цилиндра h =

Ответ: Vст =

0

Теория

Чему равен объём полого цилиндра Vст если:

Формулы

Через радиусы или диаметры цилиндра

Vст = π ⋅ (r1² – r2²) ⋅ h , где r1 – внешний радиус, r2 – внутренний радиус , а h – высота

Vст = π ⋅ ((d1/2)² – (d2/2)²) ⋅ h , где d1 – внешний диаметр, d2 – внутренний диаметр, а h – высота

Через толщину стенки цилиндра

Vст = π ⋅ (d2 ⋅ δ + δ²) ⋅ h , где δ – толщина стенки цилиндра, d2 – внутренний диаметр, а h – высота

Vст = π ⋅ ((d1 – 2 ⋅ δ) ⋅ δ + δ²) ⋅ h , где δ – толщина стенки цилиндра, d1 – внешний диаметр, а h – высота

Vст = π ⋅ (2 ⋅ r2 ⋅ δ + δ²) ⋅ h , где δ – толщина стенки цилиндра, r2 – внутренний радиус, а h – высота

Vст = π ⋅ ((2 ⋅ r1 – 2 ⋅ δ) ⋅ δ + δ²) ⋅ h , где δ – толщина стенки цилиндра, r1 – внешний радиус, а h – высота

Пример №1

К примеру, посчитаем каков объём металла в трубе, если её длинна 3 метра, внешний диаметр d1=5 см, а внутренний d2=4.5 см?

Vст = 3.14 ⋅ ((5/2)² – (4.5/2)²) ⋅ 300 = 3.14 ⋅ (6.25 – 5.0625) ⋅ 300 ≈ 1119 см³

Пример №2

Теперь посчитаем объём металла в этой же 3-х метровой трубе, но возьмём внутренний радиус r2 = 2.25 см и толщину стенки δ = 0.25 см (при этом у нас должен получится тот же ответ, что и в предыдущем примере):

Vст = 3.14 ⋅ (2 ⋅ 2.25 ⋅ 0.25 + 0.25²) ⋅ 300 = 3.14 ⋅ 1.1875 ⋅ 300 ≈ 1119 см³

См. также

Источник

Главная Учёба Объем цилиндра Объём полого цилиндра

Объём полого цилиндра

Формула вычисления объема полого цилиндра часто применяются при расчете массы полой круглой трубы.

Эти онлайн калькуляторы производят расчёты по следующим формулам.
Другая Формула

Объём полого цилиндра через внутренний и наружный радиусы

Формула расчёта: V = pi*(r1[в квадрате]-r2[в квадрате])*h

Объём полого цилиндра и его боковой поверхности через внутренний и наружный радиусы

Радиус наружный (r1)
Радиус внутренний (r2)
Высота (h)

Объём полого цилиндра по толщине стенки и наружному диаметру

Формула расчёта: Объём полого цилиндра по толщине стенки и наружному диаметру, формула

Объём полого цилиндра по толщине стенки и наружному диаметру

Внешний диаметр (D)
Толщина стенки (δ)
Высота (h)

Объём полого цилиндра, вычисляемый по внутреннему диаметру и толщине стенки

Формула расчёта: V = pi*(d*δ+δ2)*h

Объём полого цилиндра, вычисляемый по внутреннему диаметру и толщине стенки

Внутренний диаметр (d)
Толщина стенки (δ)
Высота (h)

Площадь полого цилиндра

Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!

Нет комментариев.

    Оставить комментарий

    Заполните все поля.

    Ваше имя:

    Оценка
Источник

расчет параметров гидроцилиндра по его размерам

Если известны геометрические размеры цилиндра, то можно вычислить площади поршня и объемы полостей цилиндра.

Если известно давление гидравлической системы, то дополнительно можно вычислить усилие при выдвижении и втягивании штока.

Мощность и скорость при выдвижении и втягивании штока можно определить, зная подачу (расход) рабочей жидкости от насоса.

Если вы хотите купить расчет параметров гидроцилиндра по его размерам , вы можете:

Ещё из раздела расчет гидропривода

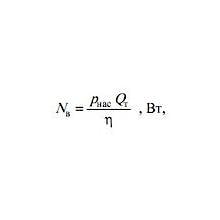
Этот калькулятор позволяет Вам вычислить три параметра, важные для проектирования гидравлической станции: – скорость потока Q (л/мин); – мощность N (кВт); – давление P (бар). Чтобы вычислить потребную мощность N (кВт) , Вы должны ввести следующие …

Для правильного расчета должно быть известно назначение трубопровода: всасывающая магистраль, напорная или сливная. Справочник по допустимой скорости жидкости в пределах этих типов магистралей приведен ниже. Расчетная скорость жидкости (м/с) должна …

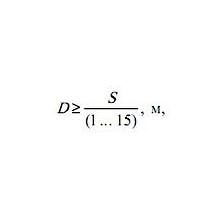
Здесь Вы можете вычислить геометрический размер цилиндра, зная необходимое усилие и рабочее давление гидроситемы. Общее усилие (Fst), Кг Количество цилиндров Давление ( P ), бар Диаметр поршня цилиндра ( fi ), мм Длина хода ( L ), мм Время …

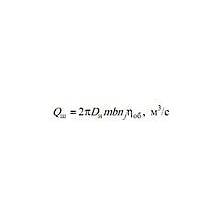
Этот калькулятор позволяет Вам вычислить или подачу Q (л/мин) или объем насоса Vg (cm3). Чтобы вычислить подачу насоса Q (l/min) , Вы должны ввести следующие данные: 1. Скорость вращения вала насоса n, для электродвигателей переменного тока это …

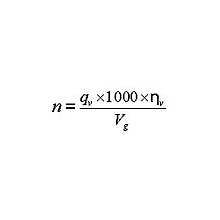
Для того чтобы вычислить количество оборотов гидромотора n (rpm), Вы должны знать следующие параметры 1) Подача насоса Q (л/мин), которая подается к гидромотору 2) коэффициент объемных потерь (КПД) , для гидромоторов он находится в диапазоне …

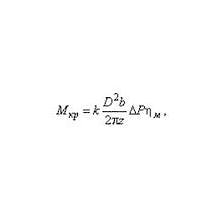
Крутящий момент на валу гидромотора М (кгм) может быть вычислен с использованием следующих параметров: 1. Давление P (бар). 2. Коэффициент объемных потерь, для гидромоторов он находится в диапазоне 0.85-0.95. 3. Объем гидромотора Vg, задается в …

Крутящий момент М (Нм), который требуется передать гидравлическому насосу от двигателя может быть вычислен с использованием следующих параметров: 1. Скорость вращения вала насоса n, для электродвигателей переменного тока это обычно – 960, 1370, 1450 …

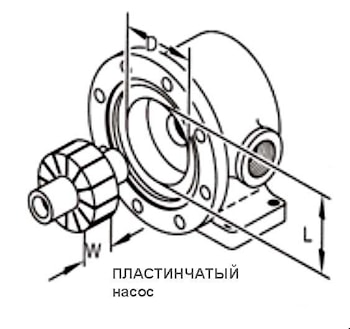
Этот калькулятор позволяет вычислить объемную подачу пластинчатого насоса за один оборот по геометрическим размерам. Тип Ширина ( W ), Диаметр ( D ), Длина ( L ) …

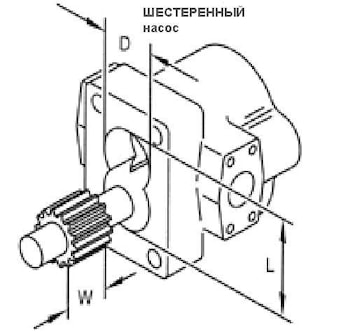
Данный калькулятор позволяет вычислить объемную подачу шестеренного насоса по его геометрическим размерам. Для этого необходимо замерить 3 размера в сантиметрах, в результате вычисления получается подача насоса с см3 за один оборот. Можно измерять в …

Источник

Объем полого цилиндра Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Высота полого цилиндра: 8 метр –> 8 метр Конверсия не требуется
Внешний радиус полого цилиндра: 10 метр –> 10 метр Конверсия не требуется
Внутренний радиус полого цилиндра: 5 метр –> 5 метр Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

1884.95559215388 Кубический метр –> Конверсия не требуется




1 Полый цилиндр Калькуляторы

Объем полого цилиндра формула

Объем полого цилиндра = pi*Высота полого цилиндра*(Внешний радиус полого цилиндра^2-Внутренний радиус полого цилиндра^2)

V = pi*h*(rOuter^2-rInner^2)

Что такое полый цилиндр?

Полый цилиндр определяется как цилиндр, который пуст внутри и имеет некоторую разницу между внутренним и внешним радиусом. Дно полого цилиндра имеет вид кольцевого кольца. Другими словами, дно полого цилиндра напоминает область, ограниченную двумя концентрическими окружностями.

Что такое цилиндр?

Цилиндр — это трехмерное твердое тело, которое содержит два параллельных основания, соединенных криволинейной поверхностью на фиксированном расстоянии. Цилиндр представляет собой трехмерную форму, состоящую из двух параллельных круглых оснований, соединенных изогнутой поверхностью. Основания всегда конгруэнтны и параллельны. Если основания имеют круглую форму, то такой цилиндр называется правильным круговым цилиндром. Если основания имеют эллиптическую форму, то это называется «эллиптическим цилиндром».

Источник

A cylinder is a three-dimensional object that is formed when a rectangle is rotated along any of its sides. A hollow cylinder is one type of cylinder that is hollow from the inside. A hollow cylinder can be defined as a three-dimensional geometric object that is empty from the inside. A hollow cylinder consists of two circular bases that have inner and outer radii. The circular bases are similar to an annular ring, which is a region bounded by two concentric circles.

Hollow Cylinder

A cylinder, which is empty from the inside and has some difference between the internal and external radius is called as H. We can see some thickness enclosed between the inner radius and the outer radius, which is equal to the difference between the internal and external radius. The height, or altitude, of the hollow cylinder, is the perpendicular distance between its two circular bases. Straws, water pipes, tubes, toilet paper rolls, etc. are some examples of hollow cylinders that we see in our daily lives.

Hollow Cylinder

Volume of Hollow Cylinder Formula

The three-dimensional space enclosed by a hollow cylinder is referred to as its volume. For example, the maximum space that can be occupied by oil when the oil is poured into a cylindrical glass jar is the volume of the jar. Now, the formula to calculate the volume of a hollow cylinder is given as follows:

Volume of Hollow Cylinder = π(R2 -r2)h cubic units

where,
“h” is the height of the hollow cylinder,
“R” is the outer radius of the given cylinder, and
“r” is the inner radius of the given cylinder.

Volume of Hollow Cylinder Derivation

Derivation of Volume of Hollow Cylinder

We know that the formula to calculate the volume of a solid cylinder when radius (r) and height (h) is (πr2)h cubic units.

Volume of cylinder = Base area × Height = (πr2)h cubic units

Now, the volume of a hollow cylinder is equal to the difference between the volume of the external cylinder and the volume of the internal cylinder. 

Let us consider that the outer radius of the hollow cylinder is “R,” its inner radius is “r,” and “h” is the height of the cylinder.

Volume of a hollow cylinder = (Volume of the cylinder with outer radius “R” and height “h”) – (Volume of the cylinder with inner radius “r” and height “h”)

Volume of a hollow cylinder (V) = πR2 × h – πr2 × h

V = π(R2 -r2)h cubic units

How to Find the Volume of Hollow Cylinder?

Let’s take an example to understand how to calculate the volume of a hollow cylinder.

Example: Calculate the volume of a hollow cylinder whose external radius is 12 cm, the internal radius is 9 cm, and the height is 7 cm

Solution:

Step 1: Note the values of the given dimensions. Here, the external radius (R) is 12 cm, the internal radius (r) is 9 cm, and the height (h) is 7 cm.

Step 2: We know that the formula to find the volume of a hollow cylinder is [π × (R2−r2) × h] cubic units. Now, substitute the given values in the formula.

Step 3: Thus, the volume of a hollow cylinder is calculated as

V = (22/7) × (122 – 92) × 7
V = 1,386 cm3

Solved Examples on Volume of Hollow Cylinder

Example 1: Calculate the volume of a hollow cylinder whose external radius is 10 cm, the internal radius is 5 cm, and the height is 8 cm [Use π= 22/7]

Solution:

External Radius (R) = 10 cm

Internal Radius (r) = 5 cm

Height (h) = 8 cm

We know that,

The volume of a hollow cylinder = π × (R2−r2) × h cubic units
                                                   = (22/7) × (102 – 52) × 8
                                                   = (22/7) × 75 × 8 
                                                   = 1,885.714 cm3

Hence, the volume of the given hollow cylinder is 1,885.714 cm3

Example 2: Calculate the volume of a hollow cylinder whose external radius is 12 inches, the internal radius is 8 inches, and the height is 6 inches. [Use π= 22/7]

Solution:

External Radius (R) = 12 inches

Internal Radius (r) = 8 inches

Height (h) = 6 inches

We know that,

The volume of a hollow cylinder = π × (R2 -r2) × h cubic units
                                                   = (22/7) × (122 – 82) × 6
                                                   = (22/7) × 80 × 6 
                                                   = 1,508.571 in3

Hence, the volume of the given hollow cylinder is 1,508.571 in3

Example 3: Determine the volume of a hollow cylindrical tube whose thickness is 4 m, the internal radius is 5 m, and the height is 8 m. [Use π= 22/7]

Solution:

Internal Radius (r) = 5 m

The thickness of the cylindrical tube = 4 m

t = R – r = 4 m

R – 5 = 4 

R = 4 + 5 = 9 m

Height (h) = 8 m

We know that,

The volume of a hollow cylinder = π × (R2 -r2) × h cubic units
                                                   = (22/7) × (92 – 52) × 8
                                                   = (22/7) × 56 × 6 = 1,408 m3

Hence, the volume of the given hollow cylinder is 1,408 m3

Example 4: Calculate the height of a hollow cylinder whose outer diameter is 16 cm, the inner diameter is 12 cm, and the volume is 792 cm3. [Use π= 22/7]

Solution:

Outer diameter = 16 cm

So, External Radius (R) = 16 cm/ 2 = 8 cm

Inner diameter = 12 cm

So, Internal Radius (r) = 12 cm/2 = 6 cm

Height = ?

We know that,

Volume of a hollow cylinder = π × (R2 -r2) × h cubic units
                                      792 = (22/7) × (82 – 62) × H
                                        H  = 9

Hence, the height of hollow cylinder is 9 cm

FAQs on Volume of Hollow Cylinder

Question 1: What is a hollow cylinder? Give some examples of a hollow cylinder.

Answer:

A hollow cylinder can be defined as a three-dimensional geometric object that is empty from the inside. A hollow cylinder consists of two circular bases that have inner and outer radii. Straws, water pipes, tubes, toilet paper rolls, etc. are some examples of hollow cylinders that we see in our daily lives.

Question 2: What is the formula to calculate the thickness of a hollow cylinder?

Answer:

The thickness of a hollow cylinder is the enclosed space between the inner radius and the outer radius, which is equal to the difference between the internal and external radius.

Thickness of the hollow cylinder (t) = R − r

where,
“R” is the outer radius of the given cylinder
“r” is the inner radius of the given cylinder

Question 3: What is the formula to calculate the total surface area of a hollow cylinder?

Answer:

The total surface area of the hollow cylinder is the sum of its curved surface area and the areas of its two circular bases.

Total Surface Area of Hollow Cylinder = [2πh (R + r) + 2π(R² – r²)] square units

where,
“h” is the height of the hollow cylinder,
“R” is the outer radius of the given cylinder, and
“r” is the inner radius of the given cylinder.

Question 4: What does the volume of a hollow cylinder change as its height triples?

Answer:

From the formula for the volume of a hollow cylinder, we can conclude that the volume is directly proportional to the height of the hollow cylinder. So, as the height of the hollow cylinder triples, its volume will also be tripled.

Related Resource

  • Area of Square
  • Area of Triangle
  • Area of Rhombus

Источник

Добавить комментарий