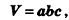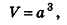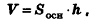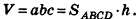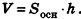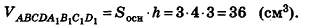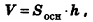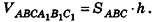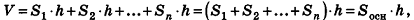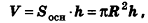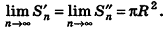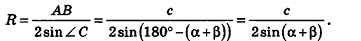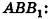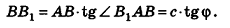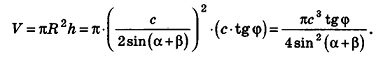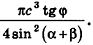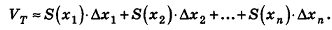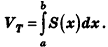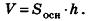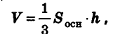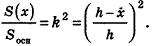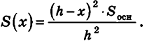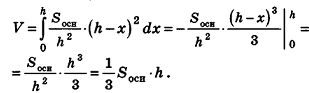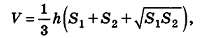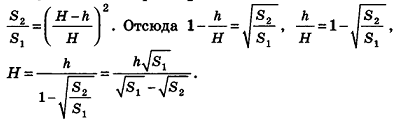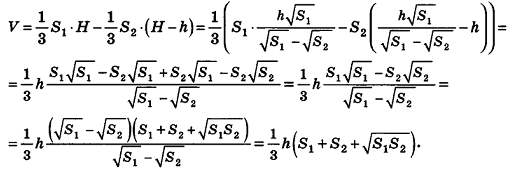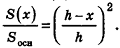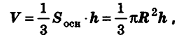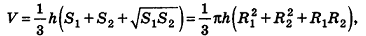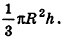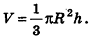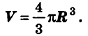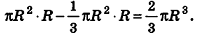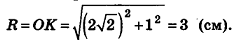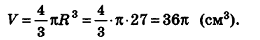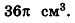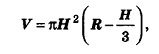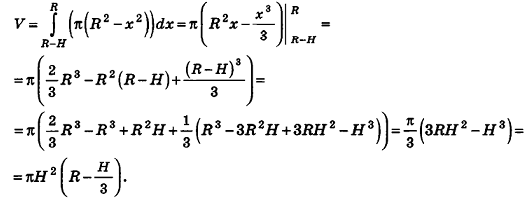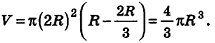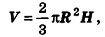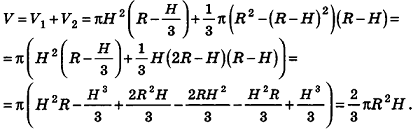На этом уроке мы введём понятия шарового сегмента,
шарового слоя и шарового сектора. А также выведем формулы для вычисления их объёмов.
Прежде чем приступить к рассмотрению данной темы,
давайте вспомним, что такое шар.
Определение:
Итак, шар
– это совокупность всех точек пространства, находящихся от данной точки на
расстоянии, не больше данного. Причём, данная точка называется центром
шара, а данное расстояние – радиусом шара.
Самой простой фигурой, которую можно начертить,
используя шар, является шаровой сегмент.
Определение:
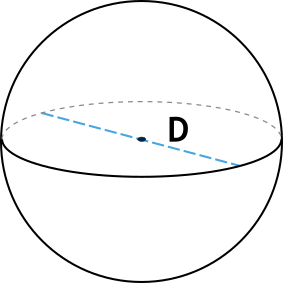
Шаровым сегментом
называется часть шара, отсекаемая от него какой-нибудь плоскостью.
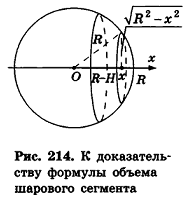
На экране вы видите, как секущая плоскость ,
проходящая через точку ,
разделяет шар на два шаровых сегмента. Круг, получившийся в сечении, называется
основанием каждого из этих сегментов, а длины отрезков и
диаметра
,
перпендикулярного к секущей плоскости, называются высотами
сегментов.
Верно следующее утверждение: если радиус шара равен ,
а высота сегмента равна ,
то объем шарового
сегмента можно вычислить по формуле:
Докажем это утверждение. Доказывать
будем с помощью определённого интеграла.
Проведём ось перпендикулярно
к плоскости .
Тогда площадь ,
при .
Вычислим объём шарового сегмента с помощью основной
формулы объёма тела. Вспомним её: .
Итак, применим основную формулу для вычисления объёмов
тел получаем, что объём шарового сегмента равен .
Что и требовалось доказать.
Заметим, что если высоту в
формуле объема шарового сегмента заменить
на ,
то получим формулу для нахождения объёма шара:
А если заменить высоту на
радиус ,
то получим формулу для нахождения объёма полушара.
Кстати, в жизни нас также окружают некоторые объекты,
имеющие форму очень близкую к форме шарового сегмента.
В современной авиации наиболее популярны парашюты в
виде сегмента.
Форму шарового сегмента нередко используют и в
архитектуре, интерьере, декоре.
Перейдём к шаровому слою.
Определение:
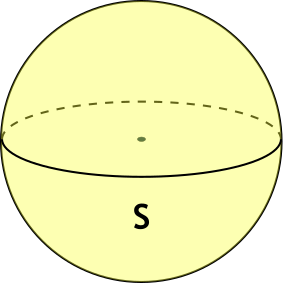
Шаровым слоем
называется часть шара, заключённая между двумя параллельными секущими плоскостями.
На экране вы видите изображение шарового слоя.
Круги, получившиеся в сечении шара плоскостями,
называются основаниями шарового слоя, а расстояние между
плоскостями – высотой шарового слоя.
Нетрудно заметить, что объём шарового слоя можно
вычислить, как разность объёмов двух шаровых сегментов.
Объём шарового слоя, изображённого на экране, равен
разности объёмов шаровых сегментов, высоты которых равны и
.
Если высота шарового слоя равна ,
а радиусы и
–
радиусы оснований шарового слоя соответственно, то объем шарового слоя можно
вычислить по формуле:
Декоративная свеча может служить примером шарового
слоя в жизни.
И теперь перейдём к шаровому сектору.
Определение:
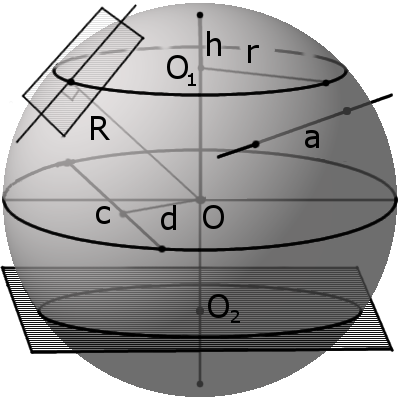
Шаровым сектором
называется тело, которое получается при вращении кругового сектора с углом,
меньшим 90о, вокруг прямой, содержащей один из ограничивающих круговой
сектор радиусов.
Обратите внимание, шаровой сектор состоит из шарового
сегмента и конуса. Причём шаровой сегмент имеет высоту ,
а конус высоту ,
где –
радиус шара.
Понятно, что шаровая поверхность пересекается с
конусом по окружности. Радиус этой окружности равен .
Если радиус шара равен ,
а высота шарового сегмента равна ,
то объем шарового
сектора можно найти по формуле:
Для того чтобы получить данную формулу необходимо
сложить объём конуса (с вершиной O), лежащего под плоскостью, и объём шарового сегмента,
лежащего над плоскостью.
Большой воздушный шар имеет форму близкую к форме
шарового сектора в жизни.
Перейдём к задачам.
Задача: радиус
шара равен см.
Вычислите объем шарового сегмента, если его высота равна см.
Решение: запишем
формулу для вычисления объёма шарового сегмента.
И подставим в неё радиус шара и высоту шарового
сегмента.
Запишем ответ.
Задача: по
разные стороны от центра шара проведены два параллельных сечения с площадью и
см2.
Расстояние между сечениями равно см.
Определите объём получившегося шарового слоя.
Решение: запишем
формулу для вычисления объема шарового слоя.
Чтобы найти объём шарового слоя нам необходимо знать
его высоту и радиусы двух его оснований.
По условию задачи нам дано расстояние между сечениями,
как раз-таки это расстояние и есть высота данного шарового слоя, и она равна .
Теперь найдём чему равны радиусы оснований шарового
слоя. Напомню, что сечением шара плоскостью является круг. Площадь круга
вычисляется по формуле .
Отсюда найдём радиусы оснований шарового слоя. Тогда имеем, радиус одного основания
равен (см),
радиус второго основания равен (см).
Подставим радиусы оснований и высоту шарового слоя в
формулу его объёма. Посчитаем. Получаем, что объём данного шарового слоя равен .
Не забудем записать ответ
Задача: радиус
шара равен см.
Найдите объем шарового сектора, если высота шарового сегмента равна см.
Решение: запишем
формулу для вычисления объёма шарового сектора.
Подставим в неё радиус шара и высоту шарового
сегмента. Посчитаем. Получим, что объём данного шарового сектора равен .
Запишем ответ.
Итоги:
На этом уроке мы ввели понятия шарового сегмента,
шарового слоя и шарового сектора. Узнали, что шаровым сегментом называется
часть шара, отсекаемая от него какой-нибудь плоскостью. Шаровым слоем
называется часть шара, заключённая между двумя параллельными секущими плоскостями.
Шаровым сектором называется тело, которое получается при вращении кругового
сектора с углом, меньшим 90о, вокруг прямой, содержащей один из ограничивающих
круговой сектор радиусов. А также вывели формулы для вычисления объёмов этих
тел.

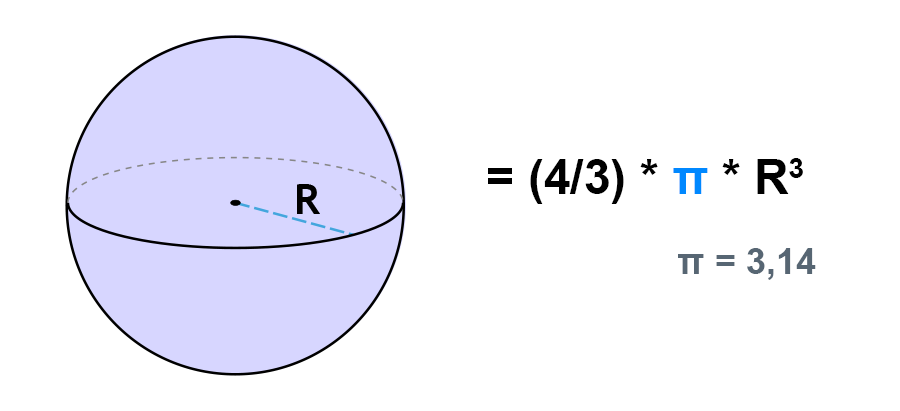
{V= dfrac{4}{3} pi R^3}
На этой странице вы можете рассчитать объем шара. Предлагаем вам 4 формулы и калькуляторы для них. Различаются они исходными данными. Вы можете найти объем шара зная его радиус, диаметр, длину окружности или площадь поверхности. Просто введите значение в калькулятор и получите мгновенный результат.
Шар – это геометрическое тело, состоящее из точек пространства, которые удалены от центра на одинаковое расстояние. Это расстояние называют радиусом шара.
Содержание:
- калькулятор объема шара
- формула объема шара через радиус
- формула объема шара через диаметр
- формула объема шара через длину окружности
- формула объема шара через площадь поверхности
- примеры задач
Формула объема шара через радиус
{V = dfrac{4}{3} pi R^3}
R – радиус шара
Формула объема шара через диаметр
{V = dfrac{1}{6} pi D^3}
D – диаметр шара
Формула объема шара через длину окружности
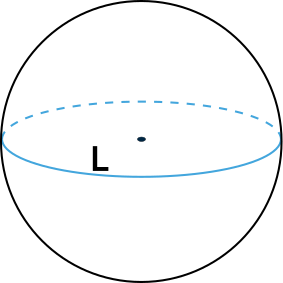
Эта формула легко выводится из формулы объема шара через его радиус и формулы для нахождения длины окружности {L = 2pi r}
{V = dfrac{L^3}{6 pi^2}}
L – длина окружности
Формула объема шара через площадь поверхности
{V = sqrt{ dfrac{S^3}{36 pi}}}
S – площадь поверхности
Примеры задач на нахождение объема параллелепипеда
Задача 1
Найдите объем шара радиус которого равен 12см.
Решение
Используем формулу шара через радиус. Просто подставим в нее значение радиуса шара и вычислим объем.
V = dfrac{4}{3} pi R^3 = dfrac{4}{3} pi cdot 12^3 = dfrac{4}{3} pi cdot 1728 = dfrac{4 cdot 1728}{3} pi = 2304 cdot pi : см^3 approx 7238.22947 : см^3
Ответ: 2304 cdot pi : см^3 approx 7238.22947 : см^3
Чтобы убедиться в правильности решения задачи, воспользуемся калькулятором .
Задача 2
Найдите объем шара диаметр которого равен 12см.
Решение
В этой задаче воспользуемся формулой шара через диаметр.
V = dfrac{1}{6} pi D^3 = dfrac{1}{6} pi cdot 12^3 = dfrac{1}{6} pi cdot 1728 = dfrac{1728}{6} pi = 288 pi : см^3 approx 904.77868 : см^3
Ответ: 288 pi : см^3 approx 904.77868 : см^3
И снова в проверке ответа нам поможет калькулятор .
Задача 3
Найдите объем шара диаметр которого равен 6см.
Решение
Эта задача аналогична задаче 2.
V = dfrac{1}{6} pi D^3 = dfrac{1}{6} pi cdot 6^3 = dfrac{1}{6} pi cdot 216 = dfrac{216}{6} pi = 36 pi : см^3 approx 113.09734 : см^3
Ответ: 36 pi : см^3 approx 113.09734 : см^3
И снова в проверке ответа нам поможет калькулятор .
Сфера, шар, сегмент и сектор. Формулы и свойства сферы
Определение.
Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).
Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение.
Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).
Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
Определение. Радиус сферы (шара) (R) – это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).
Определение. Диаметр сферы (шара) (D) – это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.
Формула. Объём шара:
| V = | 4 | πR3 = | 1 | πD3 |
| 3 | 6 |
Формула. Площадь поверхности сферы через радиус или диаметр:
S = 4πR2 = πD2
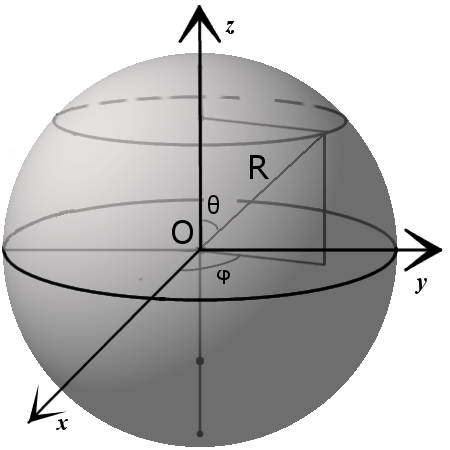
Уравнение сферы
1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат:
x2 + y2 + z2 = R2
2. Уравнение сферы с радиусом R и центром в точке с координатами (x0, y0, z0) в декартовой системе координат:
(x – x0)2 + (y – y0)2 + (z – z0)2 = R2
3. Параметрическое уравнение сферы с центром в точке (x0, y0, z0):
x = x0 + R · sin θ · cos φ
y = y0 + R · sin θ · sin φ
z = z0 + R · cos θ
где θ ϵ [0,π], φ ϵ [0,2π].
Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.
Основные свойства сферы и шара
1. Все точки сферы одинаково удалены от центра.
2. Любое сечение сферы плоскостью является окружностью.
3. Любое сечение шара плоскостью есть кругом.
4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.
5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.
6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.
7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.
8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются, а в плоскости пересечения образуется круг.
Секущая, хорда, секущая плоскость сферы и их свойства
Определение. Секущая сферы – это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.
Определение. Хорда сферы (шара) – это отрезок, соединяющий две точки сферы (поверхности шара).
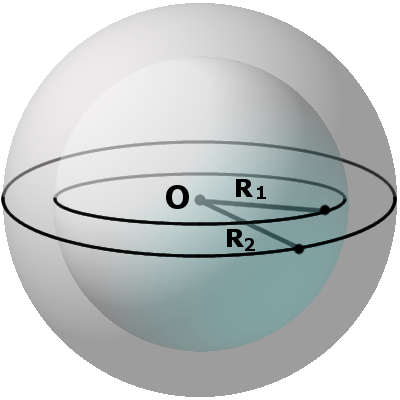
Определение. Секущая плоскость – это плоскость, которая пересекает сферу.
Определение. Диаметральная плоскость – это секущая плоскость, проходящая через центр сферы или шара, сечение образует соответственно большую окружность и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).
Любая хорда, проходящая через центр сферы (шара) является диаметром.
Хорда является отрезком секущей прямой.
Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:
d < R
Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m < R
Местом сечения секущей плоскости на сфере всегда будет малая окружность, а на шаре местом сечения будет малый круг. Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:
r = √R2 – m2,
где R – радиус сферы (шара), m – расстояние от центра шара до секущей плоскости.
Определение. Полусфера (полушар) – это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.
Касательная, касательная плоскость к сфере и их свойства
Определение.Касательная к сфере – это прямая, которая касается сферы только в одной точке.
Определение.Касательная плоскость к сфере – это плоскость, которая соприкасается со сферой только в одной точке.
Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения
Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.
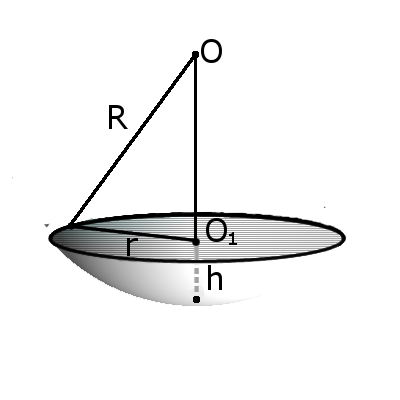
Определение. Сегмент шара – это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:
S = 2πRh
Формула. Объём сегмента сферы с высотой h через радиус сферы R:
Определение. Срез шара – это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними.
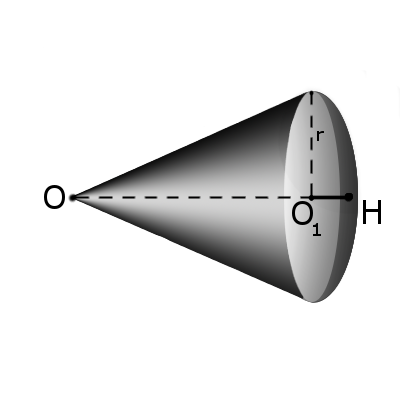
Определение. Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.
Формула. Площадь поверхности сектора S с высотой O1H (h) через радиус шара OH (R):
S = πR(2h + √2hR – h2)
Формула. Объём сектора V с высотой O1H (h) через радиус шара OH (R):
Определение. Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения. Если расстояние между центрами больше суммы радиусов, то фигуры не касаются и не пересекаются.
Определение. Концентрическими сферами называются любые две сферы, которые имеют общий центр и радиусы различной длины.
Калькулятор объема шара
Рассчитайте онлайн объем любой шарообразной фигуры по ее радиусу или диаметру.
Что известно
Длина
Размерность
Раcсчитать
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
Что такое калькулятор объема шара или сферы?
Калькулятор объема шара — это онлайн инструмент, который используется для быстрого расчета объема шара по его радиусу или диаметру. Объем шара представляет собой объем пространства, которое занимает шар в трехмерном пространстве.
Калькулятор объема шара может быть полезным инструментом для учебных заданий или практических задач, связанных с расчетами объемов шаров. Он также может использоваться в различных профессиональных областях, где необходимы точные расчеты объемов, например, в архитектуре, инженерии, физике и т.д.
🌎 Где можно применить калькулятор объема шара?
Калькулятор объема шара может быть полезным инструментом в различных областях и сферах деятельности, например:
- Архитектура и строительство: при проектировании и строительстве куполов, бассейнов, шарообразных крыш и других шарообразных конструкций.
- Медицина: при расчете объема опухолей, кровеносных сосудов, сердца и других органов.
- Производство и промышленность: при расчете объема шарообразных резервуаров, емкостей, шарообразных деталей и т.д.
- Космология: при расчете объема планет, галактик и других космических объектов.
- Физика: при расчете объема и массы материалов, например, при изучении свойств и характеристик материалов.
- Образование: при выполнении учебных заданий и проектов в школе, вузе и других образовательных учреждениях.
- Различные хобби и увлечения: при создании шарообразных фигур, скульптур, шариков для игр и других творческих проектов.
Калькулятор объема шара может быть полезным инструментом во многих ситуациях, когда необходимо быстро и точно вычислить объем шара.
🔮 В чем преимущество шарообразной формы?
Шарообразная форма имеет несколько преимуществ, которые делают ее полезной в различных областях:
- Минимальная поверхность: шарообразная форма имеет минимальную поверхность в отношении своего объема. Это значит, что на единицу объема шара приходится меньше поверхности, чем на единицу объема других форм, что может быть полезно, например, для сокращения издержек при производстве.
- Равномерность нагрузки: шарообразная форма имеет равномерное распределение нагрузки на поверхности, что позволяет ей лучше выдерживать внешнее давление.
- Сферическая симметрия: шарообразная форма имеет сферическую симметрию, что означает, что она выглядит одинаково при любом повороте вокруг своей оси. Это может быть полезным, например, при проектировании оптических систем, таких как линзы и зеркала.
- Простота: шарообразная форма является одной из самых простых геометрических форм, и ее параметры (радиус, диаметр, объем и т.д.) легко вычисляются.
- Эстетика: шарообразная форма считается эстетичной и привлекательной для взгляда. Она широко используется в дизайне, искусстве и архитектуре для создания красивых и уникальных форм.
Как вычислить объем шара через радиус?
Калькулятор объема шара обычно использует стандартную математическую формулу для расчета объема шара, которая основана на его радиусе. Формула для расчета объема шара выглядит следующим образом:
V = (4/3) * π * r3
где V – объем шара, r – радиус шара, pi – константа, примерно равная 3.14159.
Как вычислить объем шара через диаметр?
Чтобы вычислить объем шара через его диаметр, можно использовать следующую формулу:
V = (4/3) * π * (d/2)3
где V – объем шара, d – диаметр шара, π – число Пи, математическая константа, равная приблизительно 3,14159.
Для расчета объема шара нужно возвести значение d/2 в куб и умножить результат на 4/3 и на π.
❓ Вопросы и ответы
А вот несколько ответов на часто задаваемы вопросе о шаре и его объеме.
Как пользоваться онлайн калькулятором объема шара?
Для того, чтобы использовать калькулятор объема шара, нужно ввести значение радиуса шара или его диаметра в соответствующее поле калькулятора, затем калькулятор автоматически рассчитает объем шара.
Что такое шар?
Шар — это трехмерная геометрическая фигура, которая представляет собой идеальную сферу в трёхмерном пространстве. Все точки поверхности шара находятся на одинаковом расстоянии от его центра.
Для чего нужен расчет объема шара?
Расчет объема шара может быть полезен для решения различных задач в науке, технике и повседневной жизни. Например, зная объем шара, можно вычислить массу сферического объекта, если известна его плотность. Также расчет объема шара может использоваться при проектировании сферических емкостей или устройств.
Какой материал лучше всего подходит для изготовления шаров?
Для изготовления шаров часто используют различные материалы, в том числе металлы, стекло, пластмассу и резину. Выбор материала зависит от конкретной задачи и требований к изделию. Например, если необходима высокая прочность, то лучше выбрать металлический шар, а если необходимо обеспечить прозрачность, то следует выбрать стеклянный шар.
Как найти радиус шара, если известен его объем?
Радиус шара может быть найден по формуле: r = ³√(3V/4π), где r – радиус шара, V – объем шара, π – число пи (3.14159265…).
Как найти диаметр шара, если известен его радиус?
Диаметр шара равен удвоенному радиусу, то есть d = 2r, где d – диаметр шара, r – радиус шара.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Содержание:
Объёмы поверхностей геометрических тел:
То, чем в предыдущие эпохи занимались только зрелые умы ученых мужей, в более позднее время стало доступным для понимания юношей.
С древних времен люди применяли геометрию для решения конкретных житейских проблем — нахождения объемов сосудов, строений и кораблей, количества краски, необходимой для ремонта помещения. На основании практического опыта были разработаны методы вычисления объемов тел и площадей поверхностей. Но нахождение соответствующих формул, а тем более их доказательств заняло немало страниц в истории геометрической науки. Многие выдающиеся ученые внесли свой вклад в развитие теории объемов, а популяризаторы математики — в упрощение и доступное изложение этой теории.
Основной целью данной главы является формирование представлений об объемах и площадях поверхностей, обоснование соответствующих формул для основных пространственных фигур. Вы. научитесь использовать различные методы нахождения объемов, как строго геометрические, так и те, которые объединяют в себе геометрию и начала анализа. При изучений объемов тел полезно будет вспомнить и систематизировать материал о площадях фигур на плоскости. Подходы, которые применялись для получения основных формул площадей, будут надежным фундаментом для построения теории объемов.
В данной главе речь пойдет о всех основных фигурах, которые вы изучали в течение года, в частности о тесной связи многогранников и тел вращения. Это даст вам возможность, с одной стороны, вспомнить основные факты из курса геометрии, а с другой — на основании формул для площадей поверхностей многогранников получить соответствующие результаты для тел вращения.
Задачи данной главы содержат много геометрических конфигураций, что позволит вам переосмыслить весь курс стереометрии с точки зрения применения своих знаний на практике, в частности для нахождения, пожалуй, самых распространенных в жизни геометрических величин — объемов и площадей поверхностей. Ради этого бесценного опыта вы и изучали, в конце концов, геометрию в пространстве.
Объемы
Понятие объема хорошо известно на уровне повседневного опыта: мы покупаем пакет сока определенного объема, рассчитываем, какой объем займет в квартире новая мебель, берем для приготовления блюда кастрюлю соответствующего объема. Придадим этим наглядным представлениям об объеме тела определенную математическую строгость.
Понятие объема многогранников
Для дальнейших рассуждений полезно объединить практический опыт и известную уже теорию площадей многоугольников. По аналогии с ней мы и будем строить теорию объемов пространственных тел, в первую очередь многогранников.
Объем характеризует величину части пространства, которую занимает геометрическое тело, и измеряется, как и площадь, в определенных единицах. Единицей измерения площадей является площадь единичного квадрата, а за единицу измерения объема принимается объем единичного куба, то есть куба, ребро которого равно единице длины. Например, если за единицу измерения длины принимается 1 мм, 1 см, 1 дм или 1 м, то за единицу измерения объема принимается объем куба с ребром 1 мм, 1 см, 1 дм или 1 м. Соответствующая единица объема называется кубическим миллиметром (1 мм3), кубическим сантиметром (1 см3), кубическим дециметром или литром (1 дм3 или 1 л), кубическим метром (1 м3). Таким образом, вычисление объемов тел разной формы основано на сравнении с объемом единичного куба.
Измерить объем тела на практике можно, например, погрузив его в воду и подсчитав количество вытесненной телом воды. Но во многих случаях это не целесообразно, поэтому очень полезно вывести и научиться применять формулы для вычисления объемов. Соответствующая теория основана на аксиомах объема многогранников.
- Равные многогранники имеют равные объемы.
- Бели многогранник составлен из нескольких многогранников, то его объем равен сумме объемов этих многогранников.
- Объем куба с ребром, равным единице длины, равен единице объема.
Итак, объем многогранника — это положительная величина, Числовое значение которой удовлетворяет аксиомам объема. : – Как правило, объем обозначают буквой V.
Приведенные аксиомы имеют и практическую основу. Действительно, все пакеты, имеющие форму прямоугольного параллелепипеда и одинаковые размеры, содержат одинаковое количество сока.
Тела, имеющие равные объемы, называются равновеликими.
Если же каждый из двух пакетов можно разлить в одинаковое количество маленьких пакетиков, то сумма объемов этих пакетиков будет равна объему каждого из них, то есть данные пакеты имеют одинаковый объем.
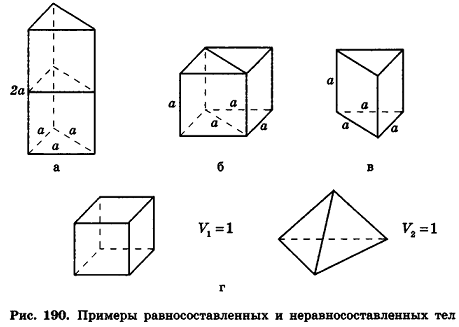
Тела, составленные из одних и тех же многогранников, называются равносоставленными. Например, равносоставленными будут тела, изображенные на рисунке 190, а, б: прямая треугольная призма и прямой параллелепипед. Действительно, каждая из этих фигур составлена из двух одинаковых прямых призм, таких как на рисунке 190, в.
Очевидно, что объемы равносоставленных многогранников равны по второй аксиоме. Интересно, что обратное утверждение неверно (в отличие от аналогичной теоремы для площадей). Так, многогранники равного объема не всегда можно разбить на конечное число равных многогранников. В частности, куб и правильный тетраэдр равных объемов (рис. 190) не являются равносоставленными.
Объем параллелепипеда
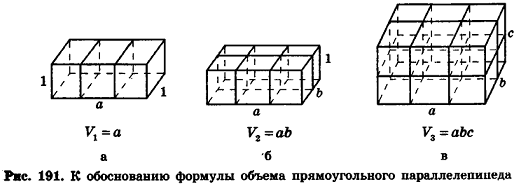
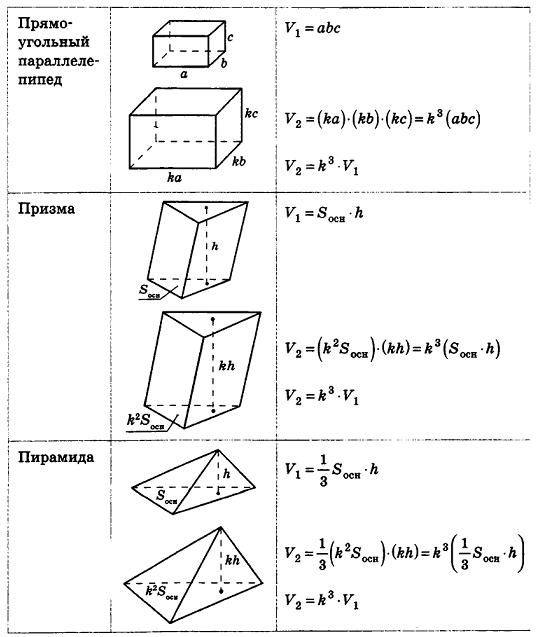
Простейшей фигурой с точки зрения вычисления объема является прямоугольный параллелепипед.
Теорема (формула объема прямоугольного параллелепипеда)
Объем прямоугольного параллелепипеда равен произведению трех его измерений:
где 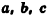
Приведем рассуждения, на которых основано доказательство данной теоремы.
Сначала рассмотрим прямоугольный параллелепипед с измерениями а, 1, 1. Так как в отрезке а единица измерения длины помещается а раз, то единичный куб помещается в параллелепипед также а раз. Значит, объем прямоугольного параллелепипеда равен а (рис. 191, а).
Аналогично объем прямоугольного параллелепипеда с измерениями 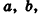
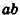
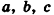
Полное доказательство данной теоремы приведено в Приложении 2.
Следствие (формула объема куба)
Объем куба равен кубу его ребра:
где а – ребро куба.
Нам известно, что площадь прямоугольника равна произведению двух его измерений, а параллелограмма — произведению его стороны на проведенную к ней высоту. По аналогии нетрудно предположить, что объем произвольного параллелепипеда также можно найти через площадь основания и соответствующую высоту.
Теорема (формула объема параллелепипеда)
Объем параллелепипеда равен произведению площади его основания на высоту:
где 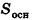
Доказательство:
Очевидно, что для прямоугольного параллелепипеда данная формула верна. Докажем ее для наклонного параллелепипеда 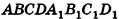
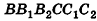
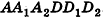
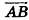
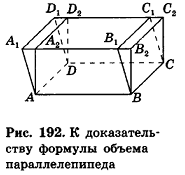
При описанном преобразовании параллелепипеда площадь его основания и высота сохраняются, а две боковые грани становятся перпендикулярными плоскости основания ABC. Если выполнить аналогичное преобразование с помощью плоскостей, проходящих через АВ и DC перпендикулярно основанию ABCD, получим прямой параллелепипед с основанием ABCD, равновеликий исходному. При этом высоты параллелепипедов также сохраняются.
Теперь проведем через точки А я В плоскости, перпендикулярные АВ (рис. 193). Дополняя прямой параллелепипед одной треугольной призмой (I) и отсекая равную ей другую призму (2), получим прямоугольный параллелепипед, равновеликий предыдущему.
Объем полученного прямоугольного параллелепипеда равен 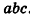
основания и высота сохраняются, то и объем исходного параллелепипеда можно вычислить с помощью полученной формулы. Итак, объем наклонного параллелепипеда
Таким образом, объем произвольного параллелепипеда вычисляется по формуле
Теорема доказана.
Пример №1
В основании наклонного параллелепипеда лежит прямоугольник со сторонами 3 см и 4 см. Боковое ребро параллелепипеда равно 6 см. Найдите объем данного параллелепипеда, если две его боковые грани перпендикулярны плоскости основания, а две другие наклонены к ней под углом 30°.
Решение:
Пусть дан параллелепипед 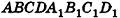
Пусть грани 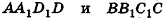
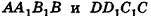
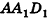
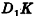
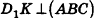
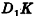
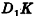
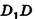
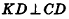
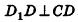
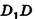
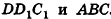
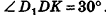
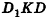
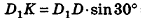
Таким образом,
Ответ: 36 см3.
Объем призмы
На плоскости для получения формулы площади треугольника было удобно дополнить треугольник до параллелограмма. Далее, для получения формулы площадей других многоугольников, целесообразно было разбить их на треугольники. Применим аналогичные приемы для вывода формулы объема призмы.
Теорема (формула объема призмы)
Объем призмы равен произведению площади ее основания на высоту:
где 
Доказательство:
Пусть дана треугольная призма 
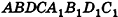
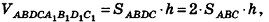
Применим только что выведенную формулу объема треугольной призмы к рассмотрению произвольной призмы.
Разобьем основание призмы на треугольники, а призму — на соответствующие треугольные призмы с высотой h (рис. 196).
По аксиоме, объем данной призмы равен сумме объемов составляющих ее треугольных призм:
где 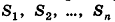
Теорема доказана.
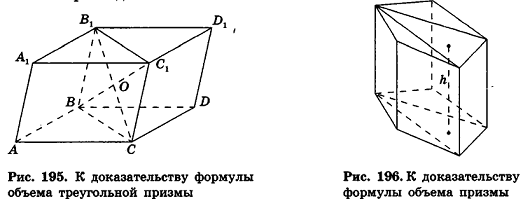
Пример №2
Объем наклонной призмы равен произведению бокового ребра на площадь перпендикулярного ему сечения: 
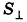
Решение:
Рассмотрим наклонную призму F1 с ребром АА1 = I (рис. 197). Проведем два ее перпендикулярных сечения, расстояние между плоскостями которых I и которые не имеют с данной призмой общих точек. При этом получим прямую призму F2 и многогранник F3 (рис. 197). Многогранник, гранник, как совмещаются параллельным переносом на вектор 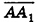
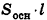
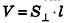
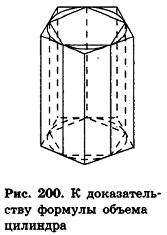
Объем цилиндра
При обосновании формулы площади круга в планиметрии мы использовали вписанные в окружности и описанные около них многоугольники. Применим аналогичные рассуждения и в пространстве, заменив круг на цилиндр, а многоугольники — на призмы. Дадим соответствующие определения.
Определение:
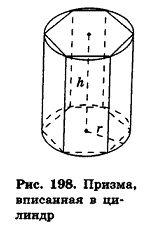
Прямая призма называется вписанной в цилиндр, если ее основания вписаны в основания цилиндра.
При этом цилиндр называется описанным около призмы. Очевидно, что боковые ребра призмы — образующие цилиндра, а высоты прямой призмы и описанного около нее цилиндра равны (рис. 198).
Определение:
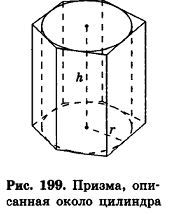
Прямая призма называется описанной около цилиндра, если ее основания описаны около оснований цилиндра.
При этом цилиндр называется вписанным в призму (рис. 199). Очевидно, что высоты прямой призмы и вписанного в нее цилиндра равны.
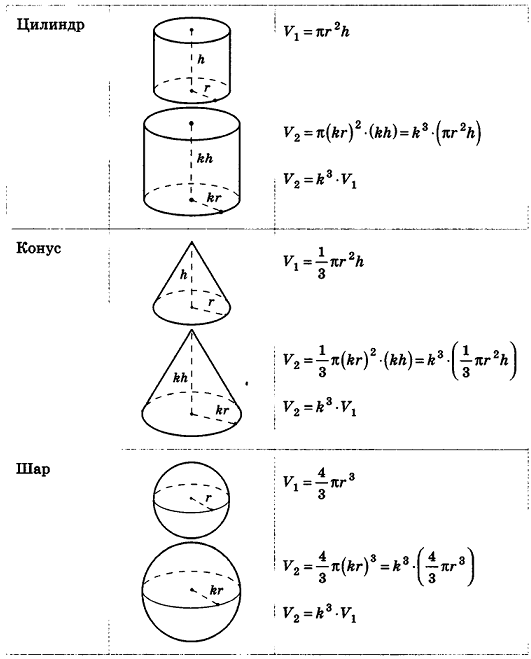
Теорема (формула объема цилиндра)
Объем цилиндра равен произведению площади его основания на высоту:
где 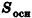
Доказательство:
Впишем в данный цилиндр радиуса R и высоты h правильную п-угольную призму с площадью основания S’n и опишем около него правильную n-угольную призму с площадью основания 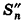
Отсюда следует, что при неограниченном возрастании п объемы вписанных призм 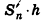
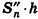
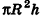
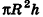
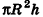
Теорема доказана.
Пример №3
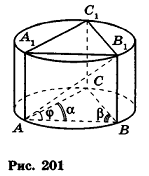
Основание прямой призмы — треугольник со стороной с-и прилежащими к ней углами 
Решение:
Пусть дана прямая треугольная призма 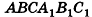
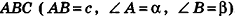
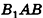
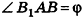
Рассмотрим цилиндр, описанный около данной призмы. Его основания описаны около оснований призмы, высота равна высоте призмы.
По теореме синусов для треугольника ABC имеем:
Из прямоугольного треугольника
Следовательно, объем цилиндра равен:
Ответ:
Объемы пирамиды, конуса и шара
Рассмотрим способ вычисления объемов тел, в основе которого лежит понятие интеграла, известное из курса алгебры и начал анализа.
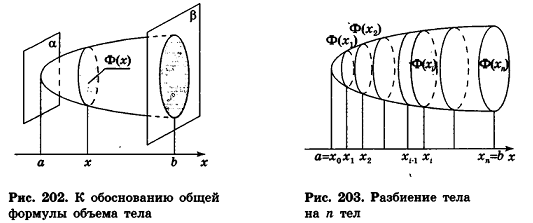
Общая формула объема
Пусть тело Т, объем которого требуется вычислить, расположено между двумя параллельными плоскостями 
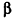
Будем рассматривать случай, когда любое сечение тела Ф(х) плоскостью, перпендикулярной-оси Ох и пересекающей эту ось в точке (х;0;0), является кругом или многоугольником (такой случай возможен, если Ф(х) — точка).
Обозначим площадь фигуры Ф(х) через S(x). Допустим, что S(x) — непрерывная функция при 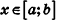
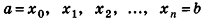
Эти плоскости разобьют тело Т на n тел: 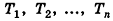
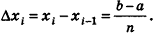
Учитывая, что объем цилиндра и призмы равен произведению площади основания на высоту, то есть 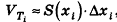
При неограниченном возрастании n правая часть данной формулы приближается сколь угодно близко к объему тела Т. С другой стороны, так как S(x) непрерывна на 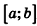
Таким образом, мы получили формулу для вычисления объема тела с помощью интеграла. Будем называть ее интегральной формулой объема.
Из этой формулы вытекает интересное и удобное в применении следствие, формулировка которого принадлежит итальянскому математику Бонавентуре Кавальери.
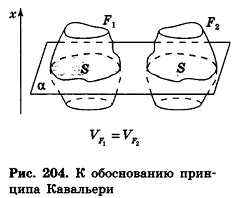
Принцип Кавальери
Если при пересечении двух тел F1 и F2 плоскостями, параллельными одной и той же плоскости а, в сечениях получаются фигуры с равными площадями, то объемы данных тел равны.
Это утверждение легко вывести из интегральной формулы объема, если расположить систему координат так, чтобы ось Ох была перпендикулярна плоскости а (рис. 204). Применение интеграла и принципа Кавальери позволяет значительно упростить нахождение формул, выражающих объемы многих важных тел.
Объем пирамиды и конуса
В пунктах 15.3 и 15.4 мы установили, что объемы призмы и цилиндра определяются одной и той же формулой:
Поэтому вполне естественно предположить, что будут совпадать формулы для объемов пирамиды и конуса.
Теорема (формула объема пирамиды)
Объем пирамиды равен трети произведения площади основания на высоту:
где 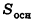
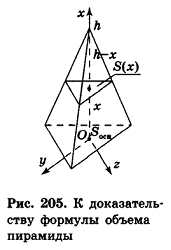
Доказательство:
Разместим пирамиду в системе координат так, чтобы ось Ох была направлена вдоль высоты, а основание’ принадлежало бы плоскости 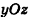
Отсюда
Применяя теперь для пирамиды интегральную формулу объема, получим:
Теорема доказана.
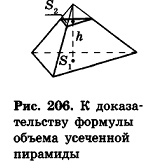
Следствие (формула объема усеченной пирамиды)
Объем усеченной пирамиды вычисляется по формуле:
где h – высота усеченной пирамиды, 
Доказательство:
Дополним данную усеченную пирамиду до полной с высотой Н (рис. 206). Тогда высота дополняющей пирамиды будет равна H-h. Из подобия полной и дополняющей пирамид, площади оснований которых равны 
По аксиомам объема, объем усеченной пирамиды равен разности объемов полной и дополняющей пирамид. Следовательно,
Формула доказана.
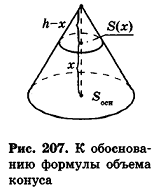
Заметим, что при доказательстве теоремы об объеме пирамиды и ее следствия, кроме интегральной формулы объема, мы применили только тот факт, что плоскость, параллельная основанию, отсекает пирамиду, для площади основания S(x) и высоты h-x которой верна формула
Но эта формула, по доказанному в п. 13.2, также верна и для конуса (рис. 207). Поэтому аналогичными формулам объема и их доказательствам для пирамиды и усеченной пирамиды будут формулы объема и их доказательства для конуса и усеченного конуса.
Теорема (формула объема конуса)
Объем конуса равен трети произведения площади основания на высоту:
где 
Следствие (формула объема усеченного конуса)
Объем усеченного конуса вычисляется по формуле
где h – высота усеченного конуса, 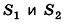
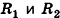
С помощью вписанных и описанных призм мы вывели формулу для объема цилиндра. Подобную связь можно установить также для конусов и пирамид.
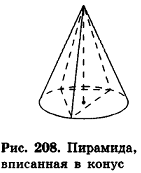
Определение:
Пирамида называется вписанной в конус, если их вершины совпадают, а основание пирамиды вписано в основание конуса.
При этом конус называется описанным около пирамиды.
Очевидно, что высоты пирамиды и описанного конуса равны, а боковые ребра пирамиды являются образующими конуса (рис. 208).
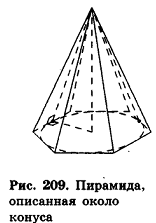
Определение:
Пирамида называется описанной около конуса, если их вершины совпадают, а основание пирамиды описано около основания конуса.
При этом конус называется вписанным в пирамиду.
Очевидно, что высоты пирамиды и вписанного конуса равны, а высоты боковых граней пирамиды являются образующими конуса (рис. 209).
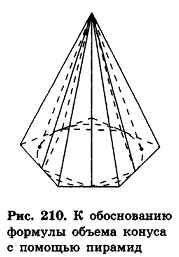
Рассмотрим правильные л-угольные пирамиды, вписанные в данный конус, и правильные л-угольные пирамиды, описанные около него (рис. 210).
Если число n сторон оснований этих пирамид неограниченно возрастает, то площади их оснований стремятся к площади круга, лежащего в основании конуса. Следовательно, их объемы стремятся 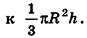
Из этих рассуждений становится понятным другое обоснование формулы объема конуса
Объем шара и его частей
Непосредственно получить только из геометрических рассуждений формулу для объема шара очень сложно. Но с помощью интегральной формулы объема и принципа Кавальери доказательство соответствующих результатов является простым и наглядным.
Теорема (формула объема шара)
Объем шара радиуса R вычисляется по формуле
Доказательство:
Найдем сначала объем полушара, применив принцип Кавальери.
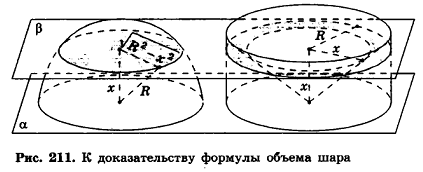
Пусть дан полушар Fl радиуса R. На плоскость а, содержащую основание полушара, поставим цилиндр, радиус и высота которого также равны R. В цилиндр впишем конус, вершина которого совпадает с центром основания цилиндра в плоскости а, а основание — с другим основанием цилиндра (рис. 211).
Сравним объем V1 полушара с объемом V2 тела F2, ограниченного нижним основанием цилиндра и боковыми поверхностями цилиндра и конуса.
Проведем плоскость 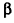
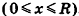
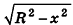
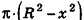
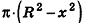
Объем шара вдвое больше объема полушара, следовательно, вычисляется по формуле 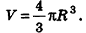
Пример №4
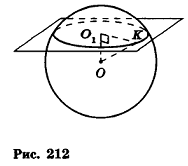
Сечение шара, удаленное от его центра на 1 см, имеет площадь 8л см2. Найдите объем шара.
Решение:
Пусть дан шар с центром О. Сечение шара некоторой плоскостью а является кругом с центром 
Пусть точка К сферы, ограничивающей шар, принадлежит данному сечению (рис. 212). Тогда площадь сечения равна 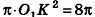
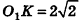
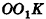
По формуле объема шара
Ответ:
Найдем теперь объемы частей шара.
Определение:
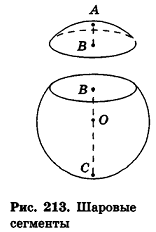
Шаровым сегментом называется часть шара, отсекаемая от него некоторой плоскостью.
На рисунке 213 плоскость сечения, проходящая через точку В, разделяет шар на два шаровых сегмента. Круг, получившийся в сечении, называется основанием этих сегментов, а длины отрезков диаметра, перпендикулярного плоскости сечения,— высотами сегментов. Так, на рисунке 213 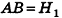
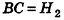
Теорема (формула объема шарового сегмента)
Объем шарового сегмента вычисляется по формуле
где R — радиус шара, Н — высота сегмента.
Доказательство:
Применим для шарового сегмента интегральную формулу объема.
Введем декартову систему координат так, чтобы ее начало совпадало с центром шара.
Тогда часть шара, ограниченная плоскостями 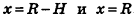
Радиус сечения шарового сегмента плоскостью, пересекающей ось Ох в точке (х;0;0), равен 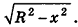
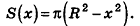
Теорема доказана.
Заметим, что при Н -2R из только что доказанной формулы следует еще один способ нахождения формулы объема шара:
Определение:
Шаровым сектором называется тело, ограниченное сферической поверхностью шарового сегмента и боковой поверхностью конуса, основанием которого является основание сегмента, а вершиной – центр шара.
Очевидно, что если шаровой сегмент меньше полушара, его дополняют конусом для получения шарового сектора; если же шаровой сегмент больше полушара, то для получения шарового сектора конус из него удаляют (рис. 215).
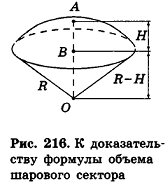
Теорема (формула объема шарового сектора)
Объем шарового сектора вычисляется по формуле
где R — радиус шара, Я — высота соответствующего шарового сегмента.
Доказательство:
Рассмотрим случай шарового сектора, высота Я соответствующего шарового сегмента для которого меньше R (рис. 216).
Тогда его объем равен сумме объема сегмента 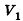
Случай, когда высота Н больше или равна R, рассмотрите самостоятельно.
Теорема доказана.
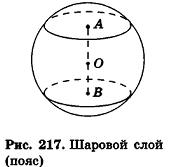
Определение:
Шаровым слоем (поясом) называется часть шара, заключенная между двумя параллельными секущими плоскостями.
Расстояние между этими плоскостями называется высотой шарового слоя, а сечения, ограничивающие слой,— основаниями шарового слоя (рис. 217).
Заметим, что объем шарового слоя можно вычислить двумя способами:
- как разность объемов двух шаровых сегментов;
- как разность объема шара и объемов двух сегментов, не входящих в слой.
Объемы подобных тел
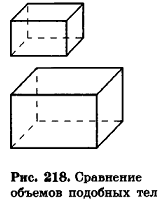
Из повседневного опыта нам хорошо известно, что при увеличении размеров предмета его объем также увеличивается. Например, легко сравнить объемы двух аквариумов, размеры одного из которых вдвое меньше соответствующих размеров другого (рис. 218): объемы отличаются в 8 раз.
Кроме того, можно проследить за подобными с коэффициентом k многоугольниками на плоскости. Как известно, их периметры отличаются в k раз, площади — в k2 раз. Естественно предположить, что объемы подобных с коэффициентом k пространственных тел отличаются к3 раз. Проверим это для тел, формулы объема которых нам уже известны.
Итак, для всех рассмотренных тел верно следующее утверждение: объемы тел, подобных с коэффициентом k, относятся как k3.
Этот факт верен и для любых простых тел, то есть тел, которые можно разбить на конечное число треугольных пирамид. В частности, любые многогранники, подобные с коэффициентом к, имеют объемы, которые отличаются в k3 раз.
Пример №5
Через середину высоты пирамиды проведена плоскость, параллельная основанию. В каком отношении она делит объем пирамиды?
Решение:
Пусть дана пирамида с вершиной S и высотой SO. Плоскость, параллельная основанию пирамиды, пересекает SO в точке 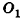
По условию = 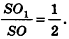
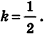
Ответ: 1:7.
- Фигуры вращения: цилиндр, конус, шар
- Объем фигур вращения
- Длина дуги кривой
- Геометрические фигуры и их свойства
- Правильные многоугольники
- Вписанные и описанные многоугольники
- Площадь прямоугольника
- Объем пространственных фигур