В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).
- Определение куба
-
Свойства куба
- Свойство 1
-
Свойство 2
- Свойство 3
-
Формулы для куба
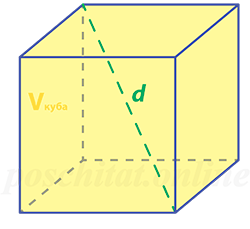
- Диагональ
- Диагональ грани
- Площадь полной поверхности
- Периметр ребер
-
Объем
- Радиус описанного вокруг шара
- Радиус вписанного шара
Определение куба
Куб – это правильный многогранник, все грани которого являются квадратами.
- Вершины куба – это точки, являющиеся вершинами его граней.
Всего их 8: A, B, C, D, A1, B1, C1 и D1. - Ребра куба – это стороны его граней.
Всего их 12: AB, BC, CD, AD, AA1, BB1, CC1, DD1, A1B1, B1C1, C1D1 и A1D1. - Грани куба – это квадраты, из которого состоит фигура.
Всего их 6: ABCD, A1B1C1D1, AA1B1B, BB1C1C, CC1D1D и AA1D1D.
Примечание: куб является частным случаем параллелепипеда или призмы.
Свойства куба
Свойство 1
Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:
- ABCD || A1B1C1D1
- AA1B1B || CC1D1D
- BB1C1C || AA1D1D
Свойство 2
Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.
- AC1 = BD1 = A1C = B1D (диагонали куба).
- О – точка пересечения диагоналей:
AO = OC1 = BO = OD1 = A1O = OC = B1O = OD.
Свойство 3
Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.
Например, на рисунке выше угол между гранями ABCD и AA1B1B является прямым.
Формулы для куба
Примем следующие обозначения, которые будут использоваться далее:
- a – ребро куба;
- d – диагональ куба или его грани.
Диагональ
Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.
Диагональ грани
Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.
Площадь полной поверхности
Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.
Периметр ребер
Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.
Объем
Объем куба равен длине его ребра, возведенной в куб.
Радиус описанного вокруг шара
Радиус шара, описанного около куба, равняется половине его диагонали.
Радиус вписанного шара
Радиус вписанного в куб шара равен половине длины его ребра.
Объём куба
- Главная
- /
- Математика
- /
- Геометрия
- /
- Объём куба
Чтобы найти объём куба воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Объём куба через ребро
Чему равен объём куба, если:
ребро a =
Vкуба =
0
Округление ответа:
Объём куба через диагональ
Чему равен объём куба, если:
диагональ d =
Vкуба =
0
Округление ответа:
Объём куба через площадь поверхности
Чему равен объём куба, если:
Sпов =
Vкуба =
0
Округление ответа:
Теория
Как найти объём куба зная длину ребра
Чему равен объём куба Vкуба, если длина его рёбер a:
Формула
Vкуба = a³
Пример
Для примера, найдём объём куба, у которого рёбра a = 5 см:
Vкуба = 5³ = 125 см³
Как найти объём куба зная диагональ
Чему равен объём куба Vкуба, если его диагональ d:
Формула
Vкуба = d³ ⁄3√3
Пример
Для примера, найдём объём куба, длина диагонали которого d = 9 см:
Vкуба = 9³ / 3√3 ≈ 729 / 5,2 ≈ 140 см³
Как найти объём куба зная площадь поверхности
Чему равен объём куба Vкуба, если площадь поверхности этого куба Sпов:
Формула
Vкуба = √Sпов³ ⁄6√6
Пример
Для примера, найдём объём куба, площадь поверхности которого Sпов = 24 см²:
Vкуба = √24³ / 6√6 = 24√24 / 6√6 = 4√4 = 8 см³
См. также
Инфоурок
›
Математика
›Другие методич. материалы›Формулы площади и объема 5 класс математика
-
Скачать материал (медленно)
Настоящий материал опубликован пользователем Булатова Айгуль Рустемовна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 5 лет и 6 месяцев
- Подписчики: 0
- Всего просмотров: 23971
-
Всего материалов:
1
Куб – это прямоугольный параллелепипед, все стороны (ребра) которого равны.
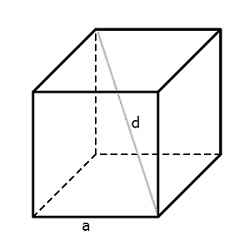
Любой куб характеризуется ребром a и диагональю d (см. рисунок). Именно эти характеристики используются в формулах куба при вычислении объема и площади.
Диагональ куба – это отрезок, соединяющий противоположные вершины куба.
Формула диагонали куба
Диагональ d куба можно получить, зная его сторону:
d2 = 3a2
Формула площади куба
Площадь поверхности куба можно получить, зная его сторону:
S = 6a2
Формула объема куба
Объем куба можно вычислить, зная его сторону:
V = a3
Поделитесь статьей с одноклассниками «КУБ формулы объема, площади поверхности, диагональ куба».
При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.
Как найти площадь и объем куба
Куб – это прямоугольный параллелепипед, все ребра которого равны. Поэтому общая формула для объема прямоугольного параллелепипеда и формула для площади его поверхности в случае куба упрощаются. Также объем куба и его площадь поверхности можно найти, зная объем шара, вписанного в него, или шара, описанного вокруг него.

Вам понадобится
- длина стороны куба, радиус вписанного и описанного шара
Инструкция
Объем прямоугольного параллелепипеда равен: V = abc – где a, b, c – его измерения. Поэтому объем куба равен V = a*a*a = a^3, где a – длина стороны куба.Площадь поверхности куба равна сумме площадей всех его граней. Всего у куба шесть граней, поэтому площадь его поверхности равна S = 6*(a^2).
Пусть шар вписан в куб. Очевидно, диаметр этого шара будет равен стороне куба. Подставляя длину диаметра в выражения для объема вместо длины ребра куба и используя, что диаметр равен удвоенному радиусу, получим тогда V = d*d*d = 2r*2r*2r = 8*(r^3), где d – диаметр вписанной окружности, а r – радиус вписанной окружности.Площадь поверхности куба тогда будет равна S = 6*(d^2) = 24*(r^2).
Пусть шар описан вокруг куба. Тогда его диаметр будет совпадать с диагональю куба. Диагональ куба проходит через центр куба и соединяет две его противоположные точки.
Рассмотрите для начала одну из граней куба. Ребра этой грани являются катетами прямоугольного треугольника, в котором диагональ грани d будет гипотенузой. Тогда по теореме Пифагора получим: d = sqrt((a^2)+(a^2)) = sqrt(2)*a.
Затем рассмотрите треугольник в котором гипотенузой будет диагональ куба, а диагональ грани d и одно из ребер куба a – его катетами. Аналогично, по теореме Пифагора получим: D = sqrt((d^2)+(a^2)) = sqrt(2*(a^2)+(a^2)) = a*sqrt(3).
Итак, по выведенной формуле диагональ куба равна D = a*sqrt(3). Отсюда, a = D/sqrt(3) = 2R/sqrt(3). Следовательно, V = 8*(R^3)/(3*sqrt(3)), где R – радиус описанного шара.Площадь поверхности куба равна S = 6*((D/sqrt(3))^2) = 6*(D^2)/3 = 2*(D^2) = 8*(R^2).
Источники:
- объем куба равен
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.