Как найти объем поверхности прямоугольного параллелепипеда формула

Параллелепипед – это многогранник с 6 гранями, каждая из которых является параллелограммом.

Прямоугольный параллелепипед – это параллелепипед, каждая грань которого является прямоугольником.

Любой параллелепипед характеризуется 3 сторонами a, b и c (см. рисунок) и диагональю. Именно эти характеристики используются в формулах параллелепипеда при вычислении объема и площади.

Диагональ параллелепипеда – это отрезок, соединяющий противоположные вершины параллелепипеда.

Формула диагонали параллелепипеда

Диагональ d прямоугольного параллелепипеда можно получить, зная его стороны:

d² = a² + b² + c²

Формула площади параллелепипеда

Площадь поверхности прямоугольного параллелепипеда можно получить, зная его стороны:

S = 2(ab + ac + bc)

Формула объема параллелепипеда

Объем прямоугольного параллелепипеда можно вычислить, зная его стороны:

V = abc

Источник

Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию, а основания представляют собой прямоугольники.

На рисунке изображен прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Его основаниями являются прямоугольники $ABCD$ и $A_1B_1C_1D_1$, а боковые ребра $AA_1, BB_1, CC_1$ и $DD_1$ перпендикулярны к основаниям.

Свойства прямоугольного параллелепипеда:

В прямоугольном параллелепипеде $6$ граней и все они являются прямоугольниками.
Противоположные грани попарно равны и параллельны.
Все двугранные углы прямоугольного параллелепипеда – прямые.
Диагонали прямоугольного параллелепипеда равны.
Прямоугольный параллелепипед имеет $4$ диагонали, которые пересекаются в одной точке и делятся в ней пополам.
Любая грань прямоугольного параллелепипеда может быть принята за основание.
Прямоугольный параллелепипед, у которого все ребра равны, называется кубом.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

$B_1D^2=AD^2+DC^2+C_1C^2$

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда.

Чтобы были понятны формулы, введем обозначения:

$а$ – длина;

$b$ – ширина;

$с$ – высота(она же боковое ребро);

$P_{осн}$ – периметр основания;

$S_{осн}$ – площадь основания;

$S_{бок}$ – площадь боковой поверхности;

$S_{п.п}$ – площадь полной поверхности;

$V$ – объем.

$V=a·b·c$ – объем равен произведению трех измерений прямоугольного параллелепипеда.

$S_{бок}=P_{осн}·c=2(a+b)·c$ – площадь боковой поверхности равна произведению периметра основания на боковое ребро.

$S_{п.п}=2(ab+bc+ac).$

Дополнительные сведения, которые пригодятся для решения задач:

Куб

$а$ – длина стороны.

$V=a^3;$

$S_{бок}=4а^2;$

$S_{п.п}=6а^2;$

$d=a√3$ – диагональ равна длине стороны, умноженной на $√3$.

Пирамида

Пирамидой называется многогранник, одна грань которого (основание) – многоугольник, а остальные грани (боковые) – треугольники, имеющие общую вершину.

Высотой ($h$) пирамиды является перпендикуляр, опущенный из ее вершины на плоскость основания.

Объем любой пирамиды равен трети произведения основания и высоты.

$V={1}/{3}S_{осн}·h$

В основании у произвольной пирамиды могут лежать различные многоугольники, рассмотрим площади некоторых из них.

В основании лежит треугольник.

Площадь треугольника.

$S={a·h_a}/{2}$, где $h_a$ – высота, проведенная к стороне $а$.
$S={a·b·sin⁡α}/{2}$, где $a,b$ – соседние стороны, $α$ – угол между этими соседними сторонами.
Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ – это полупериметр $p={a+b+c}/{2}$.
$S=p·r$, где $r$ – радиус вписанной окружности.
$S={a·b·c}/{4R}$, где $R$ – радиус описанной окружности.
Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ – катеты прямоугольного треугольника.
Для равностороннего треугольника $S={a^2√3}/{4}$, где $а$ – длина стороны.

В основании лежит четырехугольник.

Прямоугольник.
$S=a·b$, где $а$ и $b$ – смежные стороны.
Ромб.
$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ – диагонали ромба.
$S=a^2·sin⁡α$, где $а$ – длина стороны ромба, а $α$ – угол между соседними сторонами.
Трапеция.
$S={(a+b)·h}/{2}$, где $а$ и $b$ – основания трапеции, $h$ – высота трапеции.
Квадрат.
$S=a^2$, где $а$ – сторона квадрата.

Пример:

Найдите объём многогранника, вершинами которого являются точки $C, A_1, B_1, C_1, D_1$ параллелепипеда $ABCDA_1B_1C_1D_1$, у которого $AB=8, AD=12, AA_1=4$.

Решение:

Изобразим прямоугольный параллелепипед и на нем отметим вершины многогранника $C, A_1, B_1, C_1, D_1$, получим в итоге четырехугольную пирамиду. В основании пирамиды лежит прямоугольник, так основание пирамиды и прямоугольного параллелепипеда совпадают.

Объем пирамиды, в основании которой лежит прямоугольник

$V={S_{прямоугольника}·h}/{3}={a·b·h}/{3}$, где $a$ и $b$ – стороны прямоугольника.

Для нашего рисунка стороны прямоугольника – это $А_1В_1$ и $A_1D_1$.

В прямоугольном параллелепипеде противоположные ребра равны и параллельны, следовательно, $AB=А_1В_1=8; AD=A_1D_1=12$.

Высотой в пирамиде $CA_1B_1C_1D_1$ будет являться ребро $СС_1$, так как оно перпендикулярно основанию (из прямоугольного параллелепипеда).

$СС_1=АА_1=4$

$V={А_1В_1·A_1D_1·СС_1}/{3}={8·12·4}/{3}=128$

Ответ: $128$

Теорема Пифагора.

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$АС^2+ВС^2=АВ^2$

Источник

Объем, площадь и периметр прямоугольного параллелепипеда – онлайн

Объем, площадь и периметр прямоугольного параллелепипеда.

Прямоугольный параллелепипед — многогранник с шестью гранями, каждая из которых является в общем случае прямоугольником.

Противолежащие грани параллелепипеда равны. Рёбра параллелепипеда, сходящиеся в одной вершине взаимно перпендикулярны.

Объём прямоугольного параллелепипеда можно найти по формуле:

V=abc;

Площадь поверхности прямоугольного параллелепипеда равна:

S=2(ab+bc+ac);

Периметр параллелепипеда рассчитывается по следующей формуле:

P = 4a + 4b + 4c;

Объем, площадь и периметр прямоугольного параллелепипеда – калькулятор онлайн

Сторона a:

Сторона b:

Сторона c:

Найти:

V – Объем

S – Площадь

P – Периметр

Итого :

Поделиться в соц сетях:

Найти тангенс фи , если известен косинус фи

Калькулятор коэффициент мощности cos fi в tg fi Как найти тангенс фи, если известен косинус фи формула: tg φ = (√(1-cos²φ))/cos φ Калькулятор онлайн – косинус в тангенс cos φ: tg φ: Поделиться в соц сетях: Найти синус φ, если известен тангенс φ Найти косинус φ, если известен тангенс φ

Индекс Руфье калькулятор

Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание доктора Диксона о “Использование сердечного индекса Руфье в медико-спортивном контроле”. Проба Руфье – представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле: Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в

Найти косинус фи (cos φ), через тангенс фи (tg φ)

tg фи=… чему равен cos фи? Как перевести тангенс в косинус формула: cos(a)=(+-)1/sqrt(1+(tg(a))^2) Косинус через тангенс, перевести tg в cos, калькулятор – онлайн tg φ: cos φ: ± Поделиться в соц сетях:

Источник

Измерения прямоугольного параллелепипеда и его свойства

Содержание:

Что такое прямоугольный параллелепипед — определение
Свойства параллелепипеда, какими обладают противолежащие грани
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда
Как найти диагональ и ширину прямоугольного параллелепипеда

Что такое прямоугольный параллелепипед — определение

Определение

Параллелепипед — это призма с шестью гранями, в основании которой лежит параллелограмм.

Согласно другому определению, это многогранник, состоящий из шести сторон-параллелограммов.

В математике в целом, и в геометрии в частности, выделяют несколько основных видов параллелепипеда:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

прямоугольный;
прямой — параллелепипед, у которого 4 боковые грани являются прямоугольниками;
наклонный — боковые грани объемной фигуры не перпендикулярны основаниям;
ромбоэдр — шестигранная призма, грани которой — это ромбы;
куб — состоит из квадратных граней.

Определение

Прямоугольный параллелепипед — это шестигранная призма, каждая из сторон которой в общем случае является прямоугольником. Также это — многогранник, в основании которого лежит прямоугольник, а боковые грани перпендикулярны основанию.

Прямоугольных параллелепипедов в окружающем человека мире множество: комната, закрытая книга, системный блок компьютера, закрытая коробка для подарка, спичечный коробок и т. д.

Параллелепипед

Источник: wikipedia.org

Прямоугольный параллелепипед, как и любой другой, состоит из:

основания;
граней — противоположных, т. е. не имеющих общего ребра, и смежных — тех, которые имеют общее ребро;
ребер — отрезков, соединяющих соседние вершины объемной шестигранной фигуры;
диагоналей — отрезков, соединяющих противоположные вершины;
диагоналей граней;
высоты — отрезка, соединяющего верхнее и нижнее основания шестигранной призмы.

В некоторых базовых задачах просят найти количество составляющих элементов шестигранной призмы. Эти числа можно запомнить: объемная фигура состоит из 8 вершин, 12 ребер и 6 граней.

Определение

Измерениями прямоугольного параллелепипеда называют его длину, ширину и высоту.

Свойства параллелепипеда, какими обладают противолежащие грани

Вне зависимости от вида параллелепипеда, все они обладают 4 свойствами:

Противолежащие грани равны друг другу и попарно параллельны.
Все 4 диагонали шестигранника пересекаются в одной точке, которой делятся пополам. Любой отрезок, проходящий через середину диагонали, и концы которого принадлежат поверхности, также делится пополам.
Фигура симметрична относительно середины диагонали.
Квадрат длины диагонали равен сумме квадратов трех измерений.

Прямоугольный параллелепипед обладает всеми этими свойствами и несколькими специфичными, свойственными только ему.

Все стороны — прямоугольники.
Все углы, состоящие из двух граней, равны 90°.
Любую сторону можно принять за основание.
Если все ребра равны и перпендикулярны, то такой шестигранник считается кубом.

Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда

Определение

Объем прямоугольного параллелепипеда равен длине, умноженной на ширину и высоту.

(V=acdot bcdot h,)

где V — объем, a — длина, b — ширина, h — высота.

Примечание

Площадь боковой поверхности равна сумме площадей боковых граней.

(S_{бп}=2(ab+ac))

Примечание

Площадь полной поверхности равна сумме площадей боковых граней и оснований.

(S_{пп}=2(ab+bc+ac))

Как найти диагональ и ширину прямоугольного параллелепипеда

В соответствии с одним из основных свойств параллелепипеда, квадрат длины диагонали равен сумме квадратов трех измерений. Запишем в виде формулы:

(d^2=a^2+b^2+c^2)

Следовательно, длина диагонали равна квадратному корню из суммы трех измерений фигуры:

(sqrt{a^2+b^2+c^2})

Длина, ширина и высота, как правило, вычисляются через формулу объема:

(a=frac V{bh},;b=frac V{ah},;h=frac V{ab})

Существует и второй вариант, как возможно найти одно из измерений. Если известно смежное ему измерение и диагональ общей стороны шестигранника, то можно вычислить вторую сторону через теорему Пифагора или по свойствам диагонали.

Источник

Представление о том, что такое прямоугольный параллелепипед, все имеют еще с детства, когда играли в кубики, держали в руках такие предметы, как коробка из-под сока или из- под конфет, видели аквариум такой формы. В жизни мы постоянно сталкиваемся с предметами, которые представляют собой прямоугольный параллелепипед (рисунок 1).

Рисунок 1

Определение

Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками. Грань – плоская поверхность предмета, составляющая угол с другой такой же поверхностью. Основания параллелепипеда – это его верхняя и нижняя грани.

Так, на рисунке 2 показан прямоугольный параллелепипед ABCDEFGH. Он имеет 6 граней, основаниями являются грани ABCD и EFGH.

У параллелепипеда есть вершины, их 8. Они обозначены заглавными латинскими буквами. Также у прямоугольного параллелепипеда есть 12 ребер – это стороны граней: AB, BC, CD, AD, EF, FG, HG, EH, AE, BF, CG, HD.

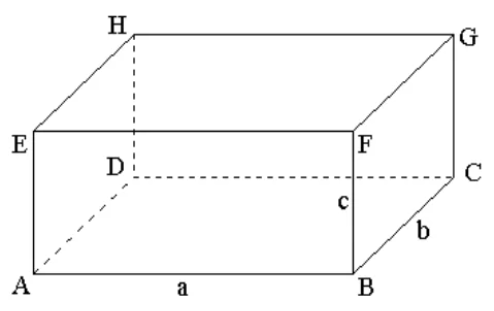
Рисунок 2

Противоположные (не имеющие общих вершин) грани прямоугольного параллелепипеда равны.

Длина, ширина, высота

Прямоугольный параллелепипед имеет три измерения – длину (а), ширину (b) и высоту (c) – рисунок 3. Зная эти измерения, можно найти не только площадь каждой грани, но и площадь всей поверхности прямоугольного параллелепипеда.

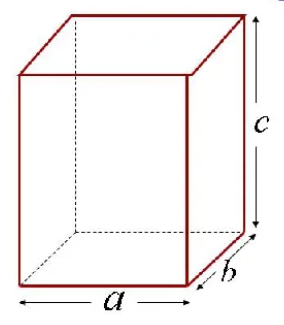
Рисунок 3

Так как каждая грань параллелепипеда – это прямоугольник, то для нахождения площади любой грани надо умножить длину и ширину этих граней, т.е S=ab, S=bc, S=ac.

Для нахождения площади поверхности прямоугольного параллелепипеда надо сложить площади всех граней, то есть S поверхности = ab+bc+ac+ab+bc+ac. Так как противоположные грани равны, то их площади тоже равны, значит S поверхности = 2ab+2bc+2ac. Это действие можно записать короче, вынося 2 за скобки, как общий множитель, то есть S поверхности = 2(ab+bc+ac). Таким образом, нахождение площади поверхности становится более быстрым.

Куб

Прямоугольный параллелепипед, у которого все измерения равны, называется кубом. Поверхность куба состоит из шести равных квадратов (рисунок 4).

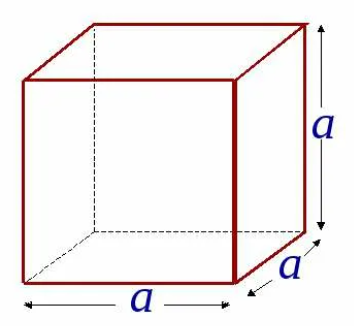
Рисунок 4

Для нахождения площади одной грани достаточно найти площадь квадрата по формуле S=a². Тогда для нахождения площади поверхности куба надо эту площадь умножить на 6, так как шесть равных граней у куба: S=6a²

Объем прямоугольного параллелепипеда

Рисунок 5

С понятием объема люди встречаются в повседневной жизни ежедневно. Мы наливаем воду в чайник, в ванну, другие жидкости в разные ёмкости – это всё измеряется в определенных единицах и является объемом. Наши шкафы, холодильники и другие подобные предметы – имеют объемы, так как мы их заполняем определенными вещами. На рисунке 5 показаны предметы, которые мы используем и которые имеют определенный объем.

Рассмотрим объемные геометрические фигуры. Так, например, прямоугольный параллелепипед. Рассмотрим рисунок 6, где показано, что параллелепипед состоит из нескольких одинаковых кубиков. Значит, объем данного параллелепипеда равен сумме объемов его кубиков.

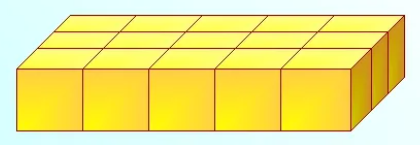
Рисунок 6

За единицу измерения объема выбирают куб, ребро которого равно единичному отрезку. Такой куб называют единичным.

Объем куба с ребром 1 мм называют кубическим миллиметром и записывают 1 мм³; с ребром 1 см – кубическим сантиметром (см³) и так далее. Измерить объем фигуры – значит подсчитать, сколько единичных кубов в ней помещается. Если объем маленького кубика на рисунке 3 принять за единицу, то объем нашего прямоугольного параллелепипеда будет равен 15 кубическим единицам.

Формула объема прямоугольного параллелепипеда

Чтобы найти объем прямоугольного параллелепипеда, надо перемножить три его измерения – длину, ширину и высоту. То есть V=abc (рисунок 4). Зная, что произведение длины и ширины – это есть площадь основания, получим, что V=(ab)h=Sh, где h – высота прямоугольного параллелепипеда. Таким образом, мы получили еще одну формулу для нахождения объема параллелепипеда.

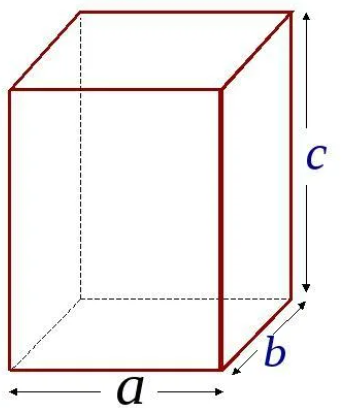
Рисунок 7

Объем куба

Поскольку у куба все ребра равны (рисунок 7), то его объем вычисляется по формуле:

V=a³

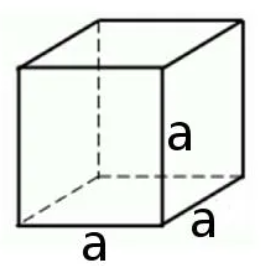
Рисунок 8

Пирамида

Рисунок 9

Прямоугольный параллелепипед является одним из видов многогранников. Также одним из видов многогранника является пирамида, образ которой также известен нам из жизни – из истории и других источников (рисунок 9).

Поверхность пирамиды состоит из боковых граней – треугольников, которые имеют общую вершину, а в её основании могут быть различные многоугольники – треугольник, четырехугольник, пятиугольник и т.д. (рисунок 10).

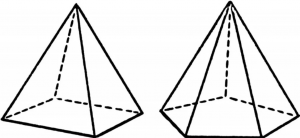
Рисунок 10

Таким образом, пирамиды можно классифицировать по количеству сторон основания (треугольная, четырехугольная, пятиугольная и т.д.). Если пирамида треугольная (рисунок 11), то её основанием может служить любая грань.

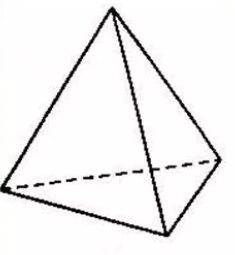
Рисунок 11

Даниил Романович | Просмотров: 893

Источник