
a – сторона куба
Формула объема куба, (V):


a, b, c – стороны параллелепипеда
Еще иногда сторону параллелепипеда, называют ребром.
Формула объема параллелепипеда, (V):
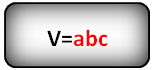

R – радиус шара
π ≈ 3.14
По формуле, если дан радиус, можно найти объема шара, (V):

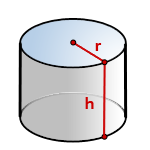
h – высота цилиндра
r – радиус основания
π ≈ 3.14
По формуле найти объема цилиндра, есди известны – его радиус основания и высота, (V):

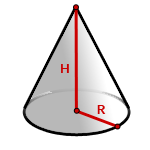
R – радиус основания
H – высота конуса
π ≈ 3.14
Формула объема конуса, если известны радиус и высота (V):
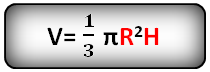
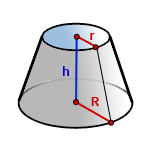
r – радиус верхнего основания
R – радиус нижнего основания
h – высота конуса
π ≈ 3.14
Формула объема усеченного конуса, если известны – радиус нижнего основания, радиус верхнего основания и высота конуса (V ):

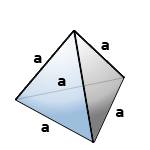
Правильный тетраэдр – пирамида у которой все грани, равносторонние треугольники.
а – ребро тетраэдра
Формула, для расчета объема правильного тетраэдра (V):
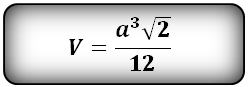
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
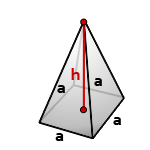
a – сторона основания
h – высота пирамиды
Формула для вычисления объема правильной четырехугольной пирамиды, (V):
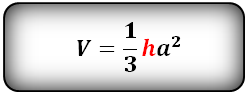
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
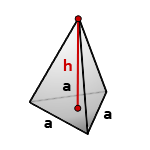
a – сторона основания
h – высота пирамиды
Формула объема правильной треугольной пирамиды, если даны – высота и сторона основания (V):

Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
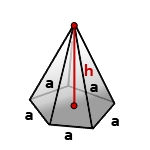
h – высота пирамиды
a – сторона основания пирамиды
n – количество сторон многоугольника в основании
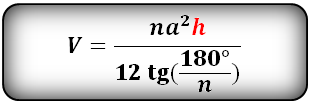
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):
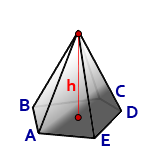
h – высота пирамиды
S – площадь основания ABCDE
Формула для вычисления объема пирамиды, если даны – высота и площадь основания (V):
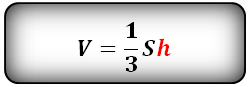
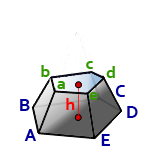
h – высота пирамиды
Sниж – площадь нижнего основания, ABCDE
Sверх – площадь верхнего основания, abcde
Формула объема усеченной пирамиды, (V):

Шаровый сегмент- это часть шара отсеченная плоскостью. В данном примере, плоскостью ABCD.

R – радиус шара
h – высота сегмента
π ≈ 3.14
Формула для расчета объема шарового сегмента, (V):
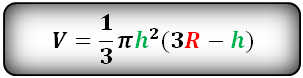
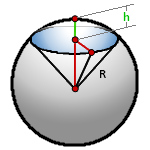
R – радиус шара
h – высота сегмента
π ≈ 3.14
Формула объема шарового сектора, (V):

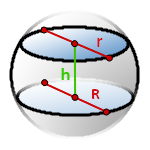
h – высота шарового слоя
R – радиус нижнего основания
r – радиус верхнего основания
π ≈ 3.14
Формула объема шарового слоя, (V):
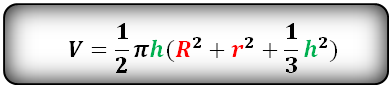
A Polygon can have any number of sides. Polygon is an irregular shape with sides as straight lines. Its volume can be said as the amount of space in it or its capacity. The below given is the simple regular polygon volume formula to find the volume of a polygon on your own. With the known values of the number of sides and the length and height per side measurements, you can calculate the capacity of a polygon using this volume of a polygon formula.
Formula:
Volume of Polygon = (A x B² x C )/ (4 x (tan(π / A)))
Where,
A = Number of sides
B = Length
C = Height
Related Calculator:
Just substitute the input measurement values in the regular polygon volume formula and do the operations to know the amount of space inside the regular polygon. Generally, volume are calculated on cm3 units.
Нахождение объема пирамиды: формула и задачи
В данной публикации мы рассмотрим, как можно найти объем пирамиды и разберем примеры решения задач для закрепления материала.
Формула вычисления объема пирамиды
1. Общая формула
Объем (V) пирамиды равняется одной третьей произведения ее высоты на площадь основания.


- ABCD – основание;
- E – вершина;
- h – высота, перпендикулярная основанию.
2. Объем правильной треугольной пирамиды

Основанием правильной треугольной пирамиды является равносторонний треугольник (ABC), площадь которого вычисляется так (а – сторона треугольника):

Подставляем данное выражение в формулу расчета объема фигуры и получаем:

3. Объем правильной четырехугольной пирамиды

Основанием правильной четырехугольной пирамиды является квадрат, площадь которого считается так: S = a 2 , где а – длина его стороны.
Следовательно, формулу объема можно представить в виде:

4. Объем правильной шестиугольной пирамиды

Основанием правильной шестиугольной пирамиды является правильный шестиугольник, площадь которого вычисляется по формуле (а – сторона основания):

С учетом этого, объем фигуры считается так:

Примеры задач
Задание 1
Найдите объем правильной треугольной пирамиды, если известно, что ее высота составляет 16 см, а длина стороны ее основания – 8 см.
Решение:
Воспользуемся соответствующей формулой, подставив в нее известные значения:
Задание 2
Высота правильной четырехугольной пирамиды равна 12 см, а сторона ее основания – 3 см. Найдите объем фигуры.
Решение:
Площадь квадрата, который является основанием пирамиды, равна 9 см 2 (3 см ⋅ 3 см). Следовательно, объем равен:
Все формулы объемов геометрических тел
1. Расчет объема куба
a – сторона куба
Формула объема куба, (V):
2. Найти по формуле, объем прямоугольного параллелепипеда
a , b , c – стороны параллелепипеда
Еще иногда сторону параллелепипеда, называют ребром.
Формула объема параллелепипеда, (V):
3. Формула для вычисления объема шара, сферы
R – радиус шара
По формуле, если дан радиус, можно найти объема шара, (V):
4. Как вычислить объем цилиндра ?
h – высота цилиндра
r – радиус основания
По формуле найти объема цилиндра, есди известны – его радиус основания и высота, (V):
5. Как найти объем конуса ?
R – радиус основания
H – высота конуса
Формула объема конуса, если известны радиус и высота (V):
7. Формула объема усеченного конуса
r – радиус верхнего основания
R – радиус нижнего основания
h – высота конуса
Формула объема усеченного конуса, если известны – радиус нижнего основания, радиус верхнего основания и высота конуса (V ):
8. Объем правильного тетраэдра
Правильный тетраэдр – пирамида у которой все грани, равносторонние треугольники.
а – ребро тетраэдра
Формула, для расчета объема правильного тетраэдра (V):
9. Объем правильной четырехугольной пирамиды
Пирамида, у которой основание квадрат и грани равные, равнобедренные треугольники, называется правильной четырехугольной пирамидой.
a – сторона основания
h – высота пирамиды
Формула для вычисления объема правильной четырехугольной пирамиды, (V):
10. Объем правильной треугольной пирамиды
Пирамида, у которой основание равносторонний треугольник и грани равные, равнобедренные треугольники, называется правильной треугольной пирамидой.
a – сторона основания
h – высота пирамиды
Формула объема правильной треугольной пирамиды, если даны – высота и сторона основания (V):
11. Найти объем правильной пирамиды
Пирамида в основании, которой лежит правильный многоугольник и грани равные треугольники, называется правильной.
h – высота пирамиды
a – сторона основания пирамиды
n – количество сторон многоугольника в основании
Формула объема правильной пирамиды, зная высоту, сторону основания и количество этих сторон (V):
Формулы и свойства правильной четырехугольной пирамиды. Усеченная пирамида
Когда человек слышит слово “пирамида”, то сразу вспоминает величественные египетские сооружения. Тем не менее древние каменные гиганты являются лишь одним из представителей класса пирамид. В данной статье рассмотрим с геометрической точки зрения свойства правильной четырехугольной пирамиды .
Что такое пирамида в общем случае?
В геометрии под ней понимают объемную фигуру, получить которую можно, если соединить все вершины плоского многоугольника с одной единственной точкой, лежащей в другой плоскости, чем этот многоугольник. Рисунок ниже показывает 4 фигуры, которые удовлетворяют данному определению.
 Вам будет интересно: Литовские статуты: даты и история изданий, регламент, хронология принятия статутов
Вам будет интересно: Литовские статуты: даты и история изданий, регламент, хронология принятия статутов
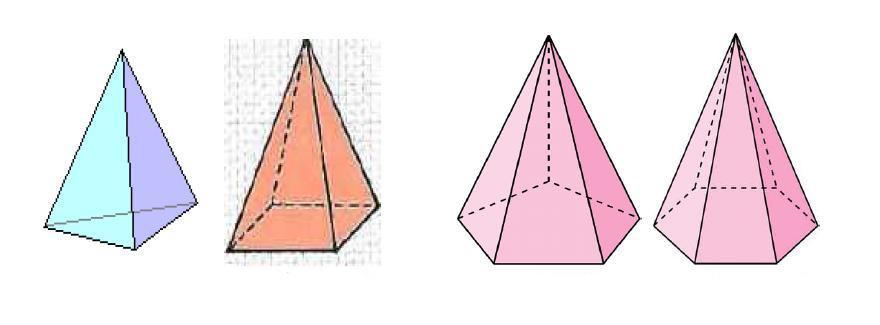
Мы видим что первая фигура имеет треугольное основание, вторая – четырехугольное. Две последние представлены пяти- и шестиугольным основанием. Однако боковая поверхность всех пирамид образована треугольниками. Их число точно равно количеству сторон или вершин многоугольника в основании.
Особым типом пирамид, которые от остальных представительниц класса отличаются идеальной симметрией, являются правильные пирамиды. Чтобы фигура была правильной, должны выполняться следующие два обязательных условия:
- в основании должен находиться правильный многоугольник;
- боковая поверхность фигуры должна состоять из равных равнобедренных треугольников.
Отметим, что второе обязательное условие можно заменить иным: перпендикуляр, проведенный к основанию из вершины пирамиды (точка пересечения боковых треугольников), должен пересекать это основание в его геометрическом центре.
Правильная четырехугольная пирамида
Теперь перейдем к теме статьи и рассмотрим, какие свойства правильной четырехугольной пирамиды характеризуют ее. Сначала покажем на рисунке, как выглядит эта фигура.

Ее основание является квадратом. Боковые стороны представляют 4 одинаковых равнобедренных треугольника (они также могут быть равносторонними при определенном соотношении длины стороны квадрата и высоты фигуры). Опущенная из вершины пирамиды высота пересечет квадрат в его центре (точка пересечения диагоналей).
Эта пирамида имеет 5 граней (квадрат и четыре треугольника), 5 вершин (четыре из них принадлежат основанию) и 8 ребер. Ось симметрии четвертого порядка, проходящая через высоту пирамиды, переводит ее в саму себя путем поворота на 90o.
Египетские пирамиды в Гизе являются правильными четырехугольными.
Далее приведем формулы, позволяющие определить все характеристики этой фигуры.
Четыре основных линейных параметра
Начнем рассмотрение математических свойств правильной четырехугольной пирамиды с формул высоты, длины стороны основания, бокового ребра и апофемы. Сразу скажем, что все эти величины связаны друг с другом, поэтому достаточно знать только две из них, чтобы однозначно вычислить оставшиеся две.
Предположим, что известна высота h пирамиды и длина a стороны квадратного основания, тогда боковое ребро b будет равно:
Теперь приведем формулу для длины ab апофемы (высота треугольника, опущенная на сторону основания):
Очевидно, что боковое ребро b всегда больше апофемы ab.
Оба выражения можно применять для определения всех четырех линейных характеристик, если известны другие два параметра, например ab и h.
Площадь и объем фигуры
Это еще два важных свойства правильной четырехугольной пирамиды . Основание фигуры имеет следующую площадь:
Эту формулу знает каждый школьник. Площадь боковой поверхности, которая образована четырьмя одинаковыми треугольниками, можно определить через апофему ab пирамиды так:
Если ab является неизвестной, то можно ее определить по формулам из предыдущего пункта через высоту h или ребро b.
Общая площадь поверхности рассматриваемой фигуры складывается из площадей So и Sb:
S = So + Sb = a2 + 2 × a × ab = a (a + 2 × ab)
Рассчитанная площадь всех граней пирамиды показана на рисунке ниже в виде ее развертки.
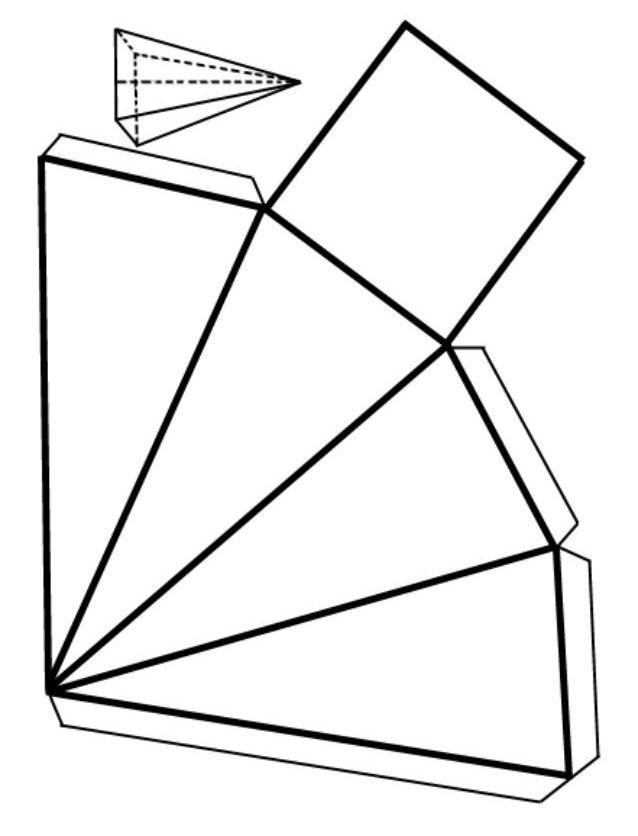
Описание свойств правильной четырехугольной пирамиды не будет полным, если не рассмотреть формулу для определения ее объема. Эта величина для рассматриваемой пирамиды вычисляется следующим образом:
То есть V равен третьей части произведения высоты фигуры на площадь ее основания.
Свойства правильной усеченной четырехугольной пирамиды
Получить эту фигуру можно из исходной пирамиды. Для этого необходимо срезать верхнюю часть пирамиды плоскостью. Оставшаяся под плоскостью среза фигура будет называться пирамидой усеченной.
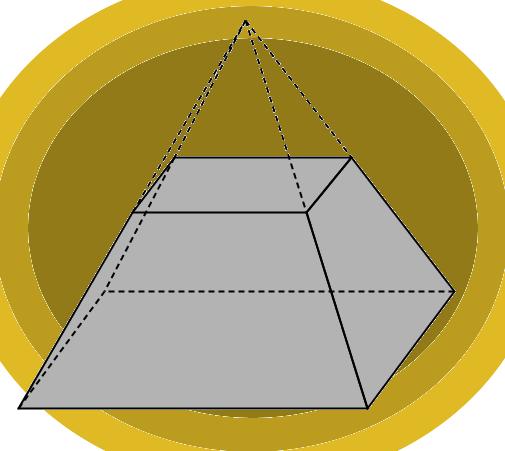
Удобнее всего изучать характеристики усеченной пирамиды, если ее основания параллельны друг другу. В этом случае нижнее и верхнее основания будут подобными многоугольниками. Поскольку в четырехугольной правильной пирамиде основание – это квадрат, то образованное при срезе сечение тоже будет представлять квадрат, но уже меньшего размера.
Боковая поверхность усеченной фигуры образована не треугольниками, а равнобедренными трапециями.
Одним из важных свойств этой пирамиды является ее объем, который рассчитывается по формуле:
V = 1/3 × h × (So1 + So2 + √(So1 × So2))
Здесь h – расстояние между основаниями фигуры, So1, So2 – площади нижнего и верхнего оснований.
[spoiler title=”источники:”]
http://www-formula.ru/2011-09-24-00-37-25
http://1ku.ru/obrazovanie/41739-formuly-i-svojstva-pravilnoj-chetyrehugolnoj-piramidy-usechennaja-piramida/
[/spoiler]

В стереометрии изучаются свойства самых разнообразных объемных тел, в том числе приводятся доказательства формул объемов многогранников от самого простого — куба — до сложных геометрических тел с n-м количеством граней.
Определение геометрических тел
Один из разделов геометрии — стереометрия — изучает самые разнообразные пространственные фигуры и их свойства. В общем случае геометрическое тело — это часть пространства, имеющая наружные границы в виде замкнутой поверхности. Сугубо геометрическое определение описывает любую пространственную форму как компактную совокупность множества точек, каждые две из которых можно соединить отрезком и он будет полностью находиться внутри заданного ограниченного контура.
Совокупность всех точек, которые находятся на границе тела, составляет его поверхность. Кроме того, можно сказать, что любое геометрическое тело образовано множеством внутренних точек. В
иды пространственных фигур:
- многогранники;
- тела вращения.
Конечное число плоских многоугольников, ограничивающих пространственное тело, называется многогранником. При этом должны соблюдаться два свойства:
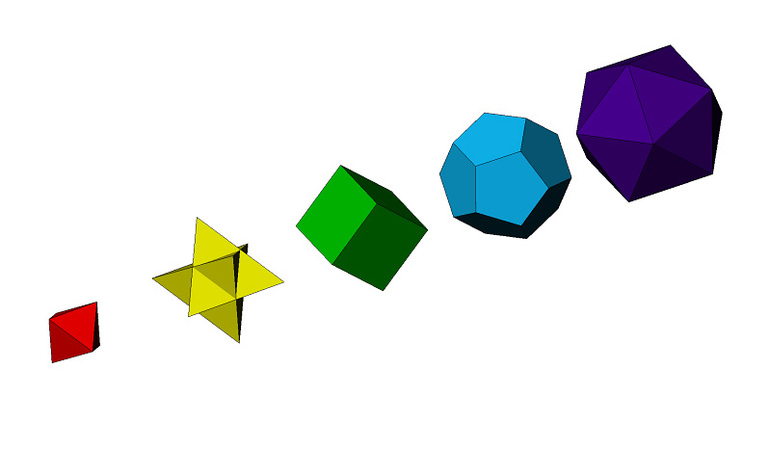
- Любая сторона каждого из многоугольников одновременно является стороной другого многоугольника и только их двоих. Соприкасающиеся стороны называются смежными.
- Все многоугольники связаны между собой — от каждого из них можно проложить путь до любого другого через смежные стороны.
В геометрии многоугольники, образующие сложный пространственный многогранник, называют гранями, отрезки, образованные местом соединения двух смежных граней — ребрами, а углы, образованные соединенными в одной точке гранями — вершинами.
Общий принцип названий таких геометрических тел заключается в указании количества их сторон.
Таким образом, если число граней обозначить n, то название образуется как n-гранник:
- 4 грани — четырехгранник;
- 5 граней — пятигранник;
- 6 граней — шестигранник;
- 8 граней — восьмигранник.
Если весь многогранник находится только с одной стороны каждой своей грани, то его называют выпуклым, в противном случае — вогнутым или невыпуклым. Звездчатые многогранники, состоящие из множества правильных пространственных фигур, относятся к невыпуклым.
Отрезок, проложенный между двумя вершинами, принадлежащими разным граням и соединяющий их — диагональ многогранника.
Понятие объема
У людей давно возникла необходимость подсчитывать или отмерять необходимое количество разных веществ.
При измерении жидких и сыпучих материалов это было сделать легко, поместив их в сосуд известного объема. Для определения вместимости любых пространственных форм в стереометрии было введено понятие объема. Величина, описывающая размер части пространства, которую занимает геометрическое тело, называется его объемом и обозначается латинской буквой V. Для величины объема верны две аксиомы:
- Полный объем любого многогранника равен сумме объемов всех его простых частей. Это свойство используется при вычислении объемов составных пространственных фигур.
- У равных тел и объемы равные, что доказывается принципом наложения, и при параллельном переносе их объем не изменяется.
На величину объема никак не влияет ни пространственное местонахождение тела, ни то, каким образом оно делится на части. Как физическая величина объем выражается через массу и плотность вещества.
Чтобы понять, какая из емкостей более вместительная, можно заполнить одну жидкостью, а потом перелить в другую и увидеть, сколько жидкости останется или не хватит. Но это очень неудобно, и при решении геометрических задач пользуются понятием единицы измерения объема. Она равна объему куба, длина ребра которого — это единица длины.
Исторически известны разные меры емкостей — бушель, галлон, ведро, бочка и т. п. , объем нефти и сейчас измеряется в баррелях. В СИ за единицу объема принят 1 кубический метр, равный количеству вещества, вмещаемого кубом с длиной грани 1 м. В стереометрии обычно используются кубические сантиметры.
Виды многогранников
Различают несколько условных классов пространственных фигур.

К обычным или классическим относятся параллелепипеды всех разновидностей, пирамиды и призмы. Правильными или Платоновыми телами называют отдельную группу из пяти многогранников, состоящих только из правильных многоугольников. Полуправильными или Архимедовыми телами называют усеченные Платоновы тела.
Отдельно рассматриваются сложные многогранники, такие как звездчатые, криволинейные или составленные из классических геометрических тел. Следует отметить, что одно и то же геометрическое тело может относиться к разным классам или являться частным случаем другого. Например, параллелепипед — частный случай призмы, а куб — правильный многогранник и частный случай параллелепипеда. Объем произвольных многогранников определяется как сумма объемов его простых частей.
Призма и параллелепипед
Такие многогранники всегда образованы двумя конгруэнтными основаниями, принадлежащими параллельным плоскостям, и n-м числом параллелограммов, являющихся их боковыми гранями. Если все ребра перпендикулярны основаниям призмы, то она называется прямой. У наклонной призмы величина углов между ребрами и основаниями отличается от 90º. Для правильной призмы обязательно выполнение условия — ее основание должно быть правильным многоугольником.
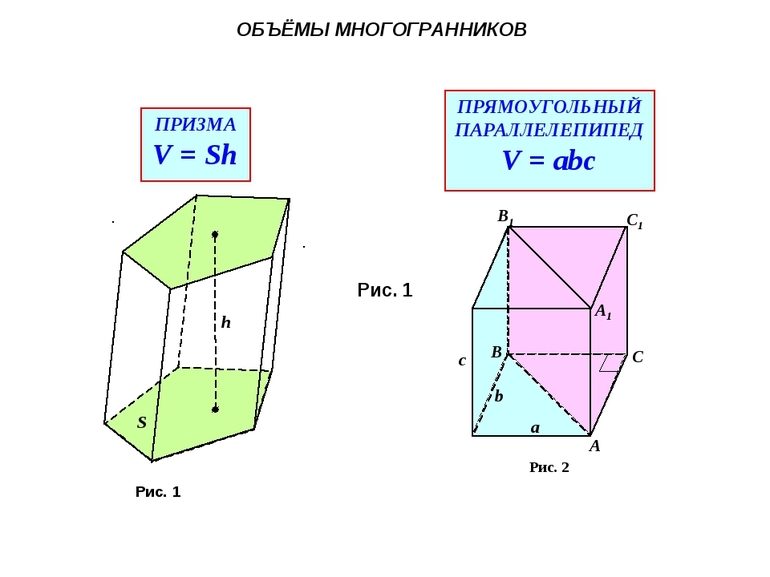
Высота — важная характеристика этого многогранника, она обозначается как h и в численном выражении представляет собой длину перпендикулярного отрезка между его основаниями. У прямой призмы высота равна длине ее ребра.
Формула для призмы: V = Sо·h, где Sо — площадь основания.
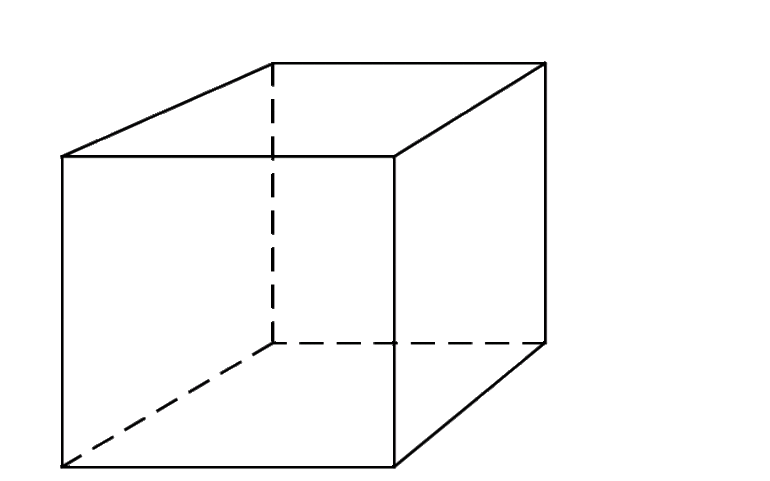
Параллелепипед является частным случаем призмы с основанием в виде четырехугольного многоугольника — параллелограмма. Тела такой формы тоже могут быть прямыми или наклонными и имеют две пары противоположных граней и четыре смежных. Если в основании параллелепипеда лежит прямоугольник, а его грани перпендикулярны основаниям, то он называется прямоугольным.
Формула объема многогранника прямоугольного параллелепипеда: V = a·b·c, где a и b — длина и ширина основания, а c — высота ребра.
К другой разновидности призм относится призматоид, если его изобразить на рисунке, то легко заметить, что грани такого тела — треугольники, одна сторона которых совпадает со стороной верхнего или нижнего основания, или трапеции, основания которых совпадают со сторонами оснований призматоида. Формула Симпсона: V = h/6 x (Sо + 4S + S1), где Sо и S1 — обозначения площадей оснований, а S — площадь параллельного и равноудаленного от оснований сечения.
Разновидности пирамиды
Пирамида представляет собой многогранник, строение которого включает в себя одно основание и n-е число треугольных граней, сходящихся в одной точке — вершине. К пирамидам относится простейший многогранник — четырехгранная пирамида, сторонами которой являются треугольники. В зависимости от того, какой многоугольник является основанием пирамиды, она может быть треугольной, четырехугольной, пятиугольной и т. д. Если при этом основания — правильные фигуры
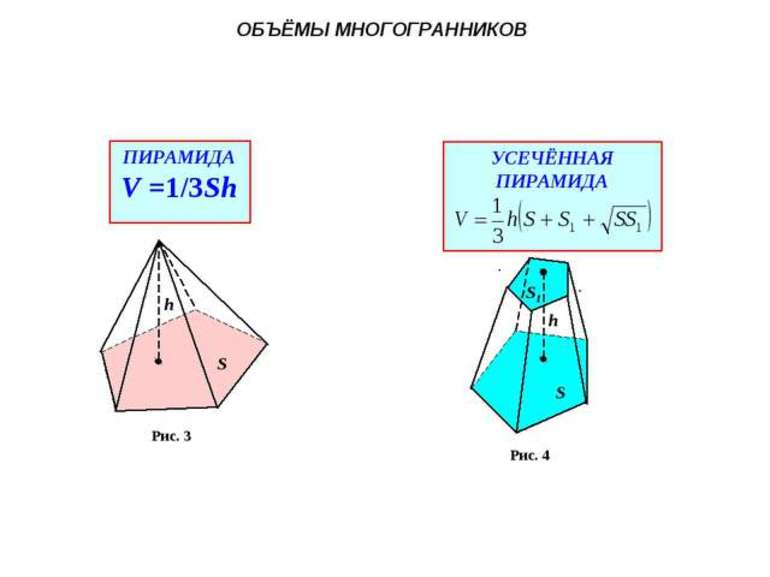
Формула расчета для пирамиды: V = 1/3 x So·h, где So — площадь основания, h — высота пирамиды, соединяющая ее вершину и центр основания.
Усеченная пирамида получается, если часть полной пирамиды отсекается параллельной основанию плоскостью. Получившееся сечение образует второе основание пирамиды.
Для усеченной пирамиды: V = 1/3 x h x (S1 + √(S1·S2) +S2), где S1 — площадь нижнего, а S2 — площадь верхнего оснований.
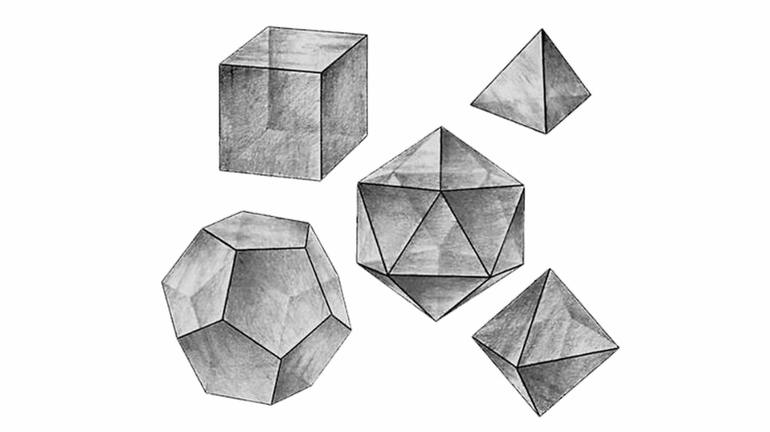
Правильные многогранники
Платоновы тела относятся к выпуклым многогранникам, обладают пространственной симметрией и состоят из одинаковых правильных многоугольников. Тетраэдр имеет форму пирамиды и состоит из четырех равносторонних треугольников. Его объем можно вычислить по стандартной формуле для пирамиды или так: V = √2/12 x a³, где a — длина ребра.
Следующий правильный многоугольник — это гексаэдр, который обычно называется кубом, у него шесть квадратных граней, следовательно, длины всех ребер равны между собой.
Формула объема куба: V = a³, где a — длина ребра.
Октаэдр имеет восемь треугольных граней. Формула объема этого правильного многогранника: V = (a³√2)/3.
Икосаэдр состоит из двадцати треугольных граней. Формула: V = (5a³(3 + √5))/12. Додекаэдр имеет 12 пятиугольных граней, а его объем вычисляется так: V = (a³(15 + 7√5))/4.
Тела вращения
Если какую-либо плоскую геометрическую фигуру вращать вокруг оси, расположенной в той же плоскости, то получится объемное тело вращения.
Шар образуется при вращении круга вокруг своей оси. Если сделать оборот прямоугольника вокруг одной из его сторон, то получится цилиндр. Конус образуется вращением треугольника по линии одного из его катетов. Окружность, вращающаяся вокруг прямой, ее не пересекающей, образует тор. Объемы сложных криволинейных тел определяются по специальной формуле с помощью интеграла.
Формулы для определения объема тел вращения приведены в таблице.
| Тело | Формула объема |
| Цилиндр | V = π R² h, R — радиус основания цилиндра, h — высота |
| Конус | V = 1/3 x π R² h, R — радиус основания конуса, h — высота |
| Шар | V = 4/3 x π R³, R — радиус, π — число пи, равное 3,14 |
Объемы деталей, представляющих собой составные многогранники можно вычислить с помощью онлайн-калькулятора.
Загрузить PDF
Загрузить PDF
Объем фигуры представляет собой занимаемое этой фигурой трехмерное пространство.[1]
Представьте себе объем как количество жидкости (или воздуха, или песка), которым можно заполнить данную фигуру. Объем измеряется в кубических единицах (мм3, см3, м3).[2]
Эта статья расскажет вам, как вычислять объем шести трехмерных фигур. Вы можете заметить, что многие формулы для вычисления объема схожи, что упрощает их запоминание.
-

1
Куб – это трехмерная фигура, которая имеет шесть одинаковых квадратных граней, то есть все ее стороны (ребра) равны.[3]
- Например, игральная кость – это куб.
-

2
Формула нахождения объема куба: V = s3, где V – объем, а s – длина ребра.
- Возведение в куб аналогично следующему умножению: s3 = s * s * s
-

3
Найдите длину стороны (ребра) куба. Она будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой). Так как ребра куба равны, измеряйте любое ребро.
- Если вы не уверены, что ваша фигура является кубом, измерьте каждую сторону, чтобы убедиться, что они равны. Если они не равны, перейдите к следующему разделу.
-

4
Подставьте длину ребра куба в формулу V = s3. Например, если ребро куба равно 5 см, напишите формулу следующим образом: V = 53 = 5 * 5 * 5 = 125 см3 – это объем куба.
-

5
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере ребро куба измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах. Если, например, сторона куба равна 3 см, то V = 33 = 27см3.
Реклама
-

1
Прямоугольный параллелепипед или прямоугольная призма – это трехмерная фигура с шестью гранями, каждая из которых является прямоугольником (вспомните коробку из под обуви). [4]
- Куб – это частный случай прямоугольного параллелепипеда, у которого все ребра равны.
-

2
Формула нахождения объема прямоугольного параллелепипеда или прямоугольной призмы: V = l*w*h, где V = объем, l = длина, w = ширина, h = высота.[5]
-

3
Длина прямоугольного параллелепипеда – это самое длинное ребро верхней или нижней грани, то есть грани, на которой стоит параллелепипед (нижняя грань) или параллельной ей грани (верхняя грань). Длина будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
- Пример: длина прямоугольного параллелепипеда равна 4 см, то есть l = 4 см.
- Не беспокойтесь о том, какие ребра выбрать в качестве длины, ширины и высоты. В любом случае в итоге вы получите правильный ответ (только измерьте три ребра, перпендикулярные друг другу).
-

4
Ширина прямоугольного параллелепипеда – это самое короткое ребро верхней или нижней грани, то есть грани, на которой стоит параллелепипед (нижняя грань) или параллельной ей грани (верхняя грань). Ширина будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
- Пример: ширина прямоугольного параллелепипеда равна 3 см, то есть w = 3 см.
- Если вы измеряете ребра параллелепипеда линейкой или рулеткой, не забудьте измерить их в одинаковых единицах измерения. Не измеряйте одно ребро в миллиметрах, а другое в сантиметрах.
-

5
Высота прямоугольного параллелепипеда – это расстояние между его нижней и верхней гранями. Высота будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
- Пример: высота прямоугольного параллелепипеда равна 6 см, то есть h = 6 см.
-

6
Подставьте найденные значения в формулу V = l*w*h.
- В нашем примере l = 4, w = 3 и h = 6. Поэтому V = 4*3*6 = 72.
-

7
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере ребра измерялись в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 72 см3.
- Если в прямоугольной призме l = 2 см, w = 4 см, h = 8 см, то V = 2*4*8 = 64 см3
Реклама
-

1
Цилиндр – это трехмерная фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее.[6]
- Например, банка или батарейка АА имеют форму цилиндра.
-

2
Формула нахождения объема цилиндра: V = πr2h, где V – объем, h – высота, r – радиус основания и πr2 – площадь основания цилиндра.
- В некоторых задачах ответ требуется представить с пи, а в некоторых вместо пи подставить 3,14.
- Формула для нахождения объема цилиндра на самом деле очень похожа на формулу вычисления объема прямоугольной призмы, то есть вы перемножаете высоту и площадь основания. В прямоугольной призме площадь основания равна l*w, а в цилиндре она равна πr2.
-

3
Найдите радиус основания. Он, скорее всего, дан в задаче. Если дан диаметр, разделите его на 2, чтобы найти радиус (d = 2r).
-

4
Если радиус не дан, измерьте его. Для этого измерьте основание цилиндра при помощи линейки или рулетки. Измеряйте основание в его самой широкой части (то есть измерьте диаметр основания), а затем разделите полученное значение на 2, чтобы найти радиус.
- Другой вариант – измерьте длину окружности цилиндра (то есть измерьте обхват цилиндра) при помощи рулетки, а затем найдите радиус по формуле r = с/2π, где с – обхват (длина окружности) цилиндра (2π = 6,28).
- Например, если обхват цилиндра равен 8 см, то радиус будет равен 1,27 см.
- Если вам нужно точное измерение, вы можете использовать оба метода, чтобы убедиться, что значения радиуса совпадают (нахождение радиуса через длину окружности является более точным методом).
-

5
Вычислите площадь круглого основания. Для этого подставьте радиус в формулу πr2.
- Если радиус основания равен 4 см, то площадь основания равна π42.
- 42 = 4 * 4 = 16. 16*π = 16*3,14 = 50,24 см2
- Если дан диаметр основания, то помните, что d = 2r. Вам нужно разделить диаметр пополам, чтобы найти радиус.
-

6
Найдите высоту цилиндра. Это расстояние между двумя круглыми основаниями. Высота будет дана в задаче или вам нужно измерить ее (линейкой или рулеткой).
-

7
Умножьте площадь основания на высоту цилиндра, чтобы найти его объем. Или же просто подставьте значения соответствующих величин в формулу V = πr2h. В нашем примере, когда радиус основания равен 4 см, а высота равна 10 см:
- V = π4210
- π42 = 50,24
- 50,24 * 10 = 502,4
- V = 502,4
-

8
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 502,4 см3.
Реклама
-

1
Пирамида – это трехмерная фигура, в основании которой лежит многоугольник, а грани являются треугольниками, имеющими общую вершину. [7]
Правильная пирамида – это трехмерная фигура, в основании которой лежит правильный многоугольник (с равными сторонами), а вершина проецируется в центр основания.[8]
- Обычно мы представляем пирамиду, имеющую квадратное основание, но в основании пирамиды может лежать многоугольник с 5, 6 или даже со 100 сторонами!
- Пирамида с круглым основанием называется конусом, который будет обсуждаться в следующем разделе.
-

2
Формула нахождения объема правильной пирамиды: V = 1/3bh, где b – площадь основания пирамиды, h – высота пирамиды (перпендикуляр, соединяющий основание и вершину пирамиды).
- Эта формула для вычисления объема пирамиды одинаково годна как для правильных пирамид (в которых вершина проецируется в центр основания), так и для наклонных (в которых вершина не проецируется в центр основания).
-

3
Вычислите площадь основания. Формула будет зависеть от фигуры, лежащей в основании пирамиды. В нашем примере в основании пирамиды лежит квадрат со стороной 6 см. Площадь квадрата равна s2, где s – сторона квадрата. Таким образом, в нашем примере площадь основания пирамиды равна 62 = 36 см2
- Площадь треугольника равна 1/2bh, где h – высота треугольника, b – сторона, к которой проведена высота.
- Площадь любого правильного многоугольника можно вычислить по формуле: А = 1/2ра, где А – площадь, р – периметр фигуры, а – апофема (отрезок, соединяющий центр фигуры с серединой любой стороны фигуры). Для получения дополнительной информации о нахождении площади многоугольников прочитайте эту статью.[9]
-

4
Найдите высоту пирамиды. Высота будет дана в задаче. В нашем примере высота пирамиды равна 10 см.
-

5
Умножьте площадь основания пирамиды на ее высоту, а затем разделите полученный результат на 3, чтобы найти объем пирамиды. Формула для вычисления объема пирамиды: V = 1/3bh. В нашем примере площадь основания равна 36, а высота равна 10, поэтому объем: 36*10*1/3 = 120.
- Если, например, дана пирамида с пятиугольным основанием площадью 26, а высота пирамиды равна 8, то объем пирамиды: 1/3*26*8 = 69,33.
-

6
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 120 см3.
Реклама
-

1
Конус – это трехмерная фигура, которая имеет круглое основание и одну вершину. Или конус – это особый случай пирамиды с круглым основанием.[10]
- Если вершина конуса находится непосредственно над центром круглого основания, то конус называется прямым; в противном случае конус называется наклонным. Но формула для вычисления объема конуса одинаковая для обоих типов конуса.
-

2
Формула для вычисления объема конуса: V = 1/3πr2h, где r – радиус круглого основания, h – высота конуса.
- b = πr2 – это площадь круглого основания конуса. Таким образом, формулу для вычисления объема конуса можно записать так: V = 1/3bh, что совпадает с формулой нахождения объема пирамиды!
-

3
Вычислите площадь круглого основания. Радиус должен быть дан в задаче. Если дан диаметр основания, то помните, что d = 2r. Вам нужно разделить диаметр пополам, чтобы найти радиус. Для вычисления площади круглого основания подставьте радиус в формулу πr2.
- Например, радиус круглого основания конуса равен 3 см. Тогда площадь этого основания равна π32.
- π32 = π(3*3) = 9π.
- = 28,27 см2
-

4
Найдите высоту конуса. Это перпендикуляр, опущенный из вершины к основанию пирамиды. В нашем примере высота конуса равна 5 см.
-

5
Перемножьте высоту конуса и площадь основания. В нашем примере площадь основания равна 28,27 см2, а высота равна 5 см, поэтому bh = 28,27 * 5 = 141,35.
-

6
Теперь умножьте полученный результат на 1/3 (или просто разделите его на 3), чтобы найти объем конуса. В описанном выше шаге вы нашли объем цилиндра, а объем конуса всегда в 3 раза меньше объема цилиндра.
- В нашем примере: 141,35 * 1/3 = 47,12 – это объем конуса.
- Или: 1/3π325 = 47,12
-

7
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 47,12 см3.
Реклама
-

1
Шар – это идеально круглая трехмерная фигура, каждая точка поверхности которой равноудалена от одной точки (центра шара). [11]
-

2
Формула для вычисления объема шара: V = 4/3πr3, где r – радиус шара.[12]
-

3
Найдите радиус шара. Радиус должен быть дан в задаче. Если дан диаметр шара, то помните, что d = 2r. Вам нужно разделить диаметр пополам, чтобы найти радиус. Например, радиус шара равен 3 см.
-

4
Если радиус не дан, вычислите его. Для этого измерьте длину окружности шара (например, теннисного мяча) в его самой широкой части при помощи веревки, нити или другого подобного предмета. Затем измерьте длину веревки, чтобы найти длину окружности. Разделите полученное значение на 2π (или на 6,28), чтобы вычислить радиус шара.
- Например, если вы измерили мяч и нашли, что длина его окружности равна 18 см, разделите это число на 6,28 и получите, что радиус мяча равен 2,87 см.
- Проделайте 3 измерения окружности шара, а затем усредните полученные значения (для этого сложите их и сумму разделите на 3), чтобы убедиться, что вы получили значение, близкое к истинному.
- Например, в результате трех измерений длины окружности вы получили следующие результаты: 18 см, 17,75 см, 18,2 см. Сложите эти значения: 18 + 17,5 + 18,2 = 53,95, а затем разделите их на 3: 53,95/3 = 17,98. Используйте это среднее значение в расчетах объема шара.
-

5
Возведите радиус в куб (r3). То есть r3 = r*r*r. В нашем примере r = 3, поэтому r3 = 3 * 3 * 3 = 27.
-

6
Теперь умножьте полученный результат на 4/3. Вы можете использовать калькулятор или выполнить умножение вручную, а затем упростить дробь. В нашем примере: 27*4/3 = 108/3 = 36.
-

7
Умножьте полученный результат на π (3,14), чтобы найти объем шара.
- В нашем примере: 36*3,14 = 113,09.
-

8
К ответу обязательно припишите соответствующие единицы измерения. В приведенном примере все величины измерялась в сантиметрах, поэтому объем будет измеряться в кубических сантиметрах: 113,09 см3.
Реклама
Об этой статье
Эту страницу просматривали 74 216 раз.
